数据分析——最小二乘法建立线性回归方程（最简单的一元线性模型为例）

别看公式多，其实很简单

最小二乘法其实又叫最小平方法，是一种数据拟合的优化技术。实质上是利用最小误差的平方寻求数据的最佳匹配函数，利用最小二乘法可以便捷的求得未知的数据，起到预测的作用，并且是的这些预测的数据与实际数据之间的误差平方和达到最小。一般应用在曲线拟合的目的上。

本篇文章不考虑其他方面的应用，我们用最简单的实例说明最小二乘法的工作原理与其内在含义。

当我们在研究两个变量（x，y）之间的相互关系时，往往会有一系列的数据对[(x1,y1),(x2,y2)... (xm,ym)],那么将这些数据描绘到x-y直系坐标中若发现这些点都在一条直线附近时，那么初始令这条直线方程的表达式为

$\widehat{Y}_i=a_0+a_1x_i$

其中 $a_0,a_1$ 是任意的实数，现在需要让当 x 取值为 $x_i$ 预测值 $Y_i$ 与回归方程所预测的 $\widehat{Y}_i$ 之间的差值平方最小，但是对于整个回归方程而言，就是所有预测值与实际值之间差值平方之和最小。

如果你要是问我，为什么要用预测值与真实值之间的差值。因为想要需要比较两个Y值，必须有个不变的因子那就是X，在同一个X下比较两种Y才有意义。如果你又问，为什么要平方，那是因为两个Y值之间做差值总会有正负的性质，而这是一个距离问题，是一个标量，所以平方。

故建立一下方程：

$\sum _{i-1}^n(Y_i-\widehat{Y}_i) = Q(a_0,a_1)$

Q为关于预测方程中两个参数 $a_0,a_1$ 的函数而已，此时将预测方程（有的人也叫拟合函数）带入以上公式得到以下方程：

$\sum _{i-1}^n(Y_i-(a_0+a_1x_i)) ^2= Q(a_0,a_1)$

要使的方程Q的取值最小，那么需要对函数Q分别对 $a_0,a_1$ 求一阶偏导数，并且零偏导之后的值为0。即

$\partial Q/\partial a_0=-2\sum _{i=1}^n(\widehat{Y}_i-a_0-a_1x_i)=0$

$\partial Q/\partial a_1=-2\sum _{i=1}^n(\widehat{Y}_i-a_0-a_1x_i)x_1=0$

然后，郁闷了一波，为什么要等于0才行啊？哎！因为函数Q是一个进行平方擦操作了的，那么Q大致的曲线就是一个凹形曲线咯，当分别对两个变量求偏导之后等于零时Q肯定处于曲线的最低点，这样也满足了预测值与真实值距离最近的条件了。

接下来就需要对两个参数进行变换求解了，经过一顿移项变换操作之后得到两个参数 $a_0,a_1$ 关于x和y的表达式。

$a_1=\frac{n\sum_{i=1}^nx_iy_i-\sum _{i=1}^nx_i\sum _{i=1}^ny_i }{n\sum _{i=1}^nx_i^2-(\sum _{i=1}^nx_i)^2}$

$a_0=\frac{\sum _{i=1}^ny_i}{n}-a_1\frac{\sum _{i=1}^nx_i}{n}$

我靠，敲得我头都晕了眼也花了，公式很难敲，关键是态度要到位。

该例子数据引用于SPSS生活统计学。

某市欲对货运总量与工业总产值的数量关系进行研究，以便通过工业总产值预测货运总量。现将1991-2000年的数据，列入表中，根据这些数据建立回归方程。

货运总量 2.8 2.9 3.2 3.2 3.4 3.2 3.3 3.7 3.9 4.2

工业总值 25 27 29 32 34 36 35 39 42 45

首先观测这些数据是否具有某种直观上的特征，

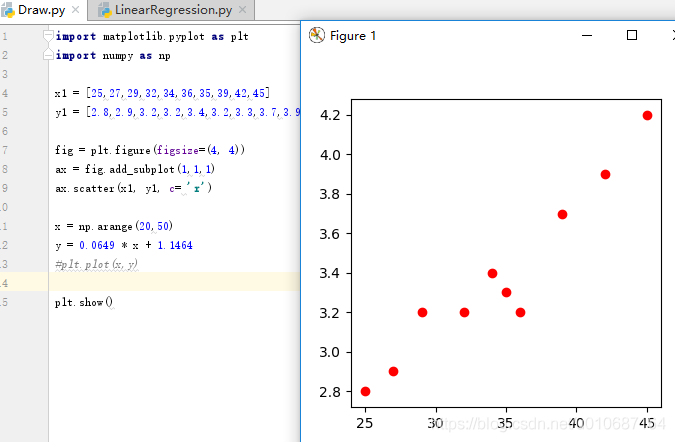
由上图可以直接看出，x与y之间存在着大致的线性关系，所以权当两者就是线性关系。接下来我们计算我们需要用到的数据计算结果xy，x平方与y平方，详见下图。

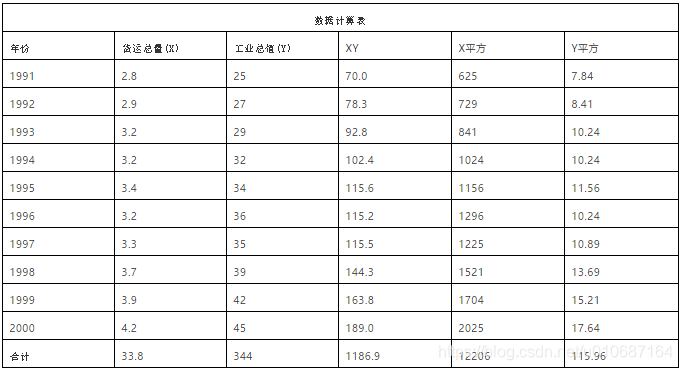
将这些结果带入公式：

$a_1=\frac{n\sum_{i=1}^nx_iy_i-\sum _{i=1}^nx_i\sum _{i=1}^ny_i }{n\sum _{i=1}^nx_i^2-(\sum _{i=1}^nx_i)^2}\approx 0.06493$

$a_0=\frac{\sum _{i=1}^ny_i}{n}-a_1\frac{\sum _{i=1}^nx_i}{n}\approx 1.1464$

那么线性回归的方程即为

$\widehat{Y}_i=a_0+a_1X_i = 1.1644+0.06493X_i$

顺便配个图：

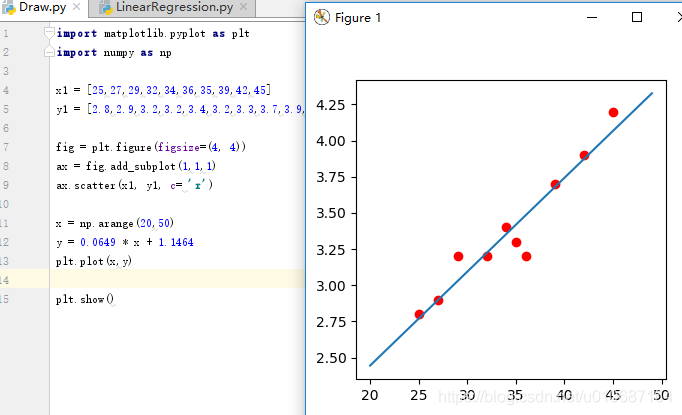
这样线性回归的方程就出来了。OK最小二乘法也说了（不是很深，也不是很广，因为自己很菜），例子应用也说了。那么本篇到此结束。