【AI基础】bias和variance的奇妙关系

一、误差Error分析

1.估测变量x的偏差和方差

【举栗子】
一次打靶实验，目标是为了打到10环，但是实际上只打到了7环，那么这里面的Error就是3。具体分析打到7环的原因，可能有两方面：

• 一是瞄准出了问题，比如实际上射击瞄准的是9环而不是10环，这里的差值1就是bias，表示模型期望和真实目标的差距；
• 二是枪本身的稳定性有问题，虽然瞄准的是9环，但是只打到了7环，这里的差值2就是variance，表示模型的稳定性，即训练得到的模型之间的变动水平。
• Error = Bias + VarianceError反映的是整个模型的准确度。

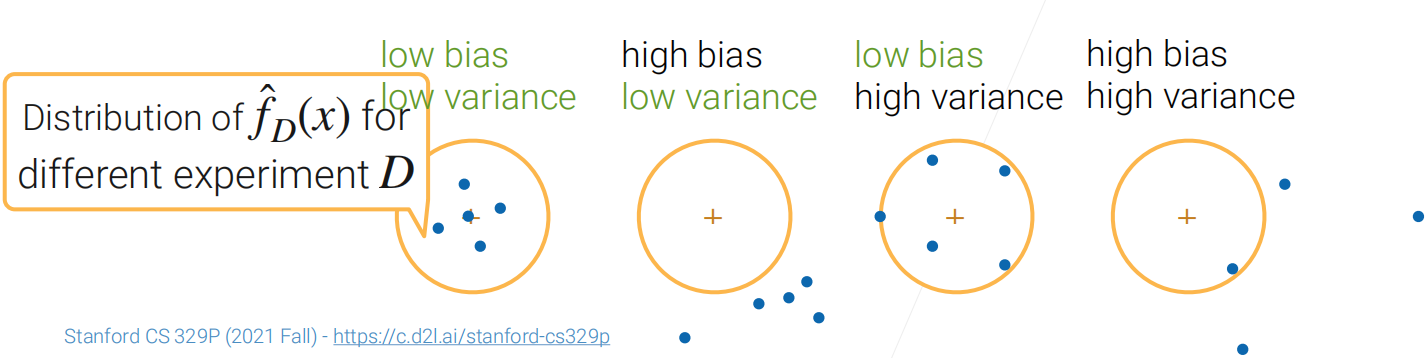
具体的公式推导如下：

• 首先假设从n个样本点中学习到$y=f(x)+\epsilon$，这里的$\epsilon$表示噪音。
• 目标是从采样到的点中学习到 $\hat{f}$，使得 $\hat{f}$ 和我们真实的$f(x)$尽可能相近，这里最简单的方法就是最小化均方误差（MSE）。注意下面的平方项木有了，因为之间相互独立。

$$\begin{array}{rl}{\mathrm{E}}_D\left[{\left(y-{\hat{f}}_D(x)\right)}^2\right]& ={\mathrm{E}}_D\left[{\left(\left(f-{\mathrm{E}}_D\left[{\hat{f}}_D\right]\right)-\left({\hat{f}}_D-{\mathrm{E}}_D\left[{\hat{f}}_D\right]\right)+\epsilon \right)}^2\right]\\ & ={\left(f-{\mathrm{E}}_D\left[{\hat{f}}_D\right]\right)}^2+{\mathrm{E}}_D{\left[\left({\hat{f}}_D-{\mathrm{E}}_D\left[{\hat{f}}_D\right]\right)\right)}^2]+{\epsilon }^2\\ & =\mathrm{Bias}{\left[{\hat{f}}_D\right]}^2+\mathrm{Var}\left[{\hat{f}}_D\right]+{\epsilon }^2\end{array}$$

2.不同模型情况

1）不同模型的方差

一次模型的方差就比较小的，也就是是比较集中，离散程度较小。而5次模型的方差就比较大，同理散布比较广，离散程度较大。

所以用比较简单的模型，方差是比较小的（就像射击的时候每次的时候，每次射击的设置都集中在一个比较小的区域内）。如果用了复杂的模型，方差就很大，散布比较开。

这也是因为简单的模型受到不同训练集的影响是比较小的。

2）不同模型的偏差

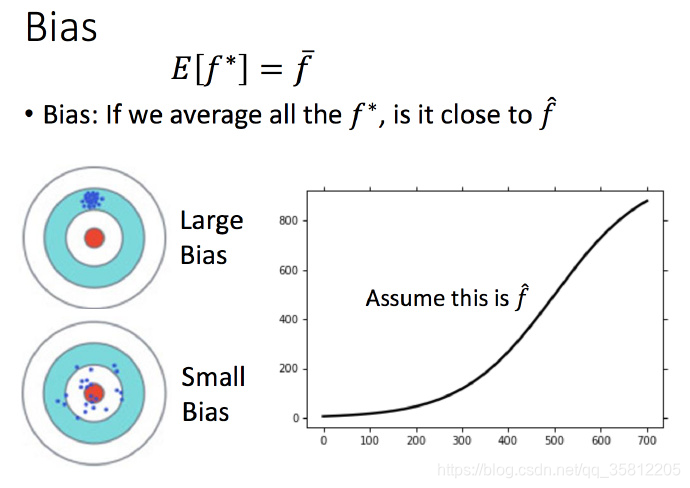
这里没办法知道真正的 $\hat{f}$，所以假设图中的那条黑色曲线为真正的 $\hat{f}$
结果可视化，一次平均的 $\bar{f}$ 没有5次的好，虽然5次的整体结果离散程度很高。

一次模型的偏差比较大，而复杂的5次模型，偏差就比较小。
直观的解释：简单的模型函数集的space比较小，所以可能space里面就没有包含靶心，肯定射不中。而复杂的模型函数集的space比较大，可能就包含的靶心，只是没有办法找到确切的靶心在哪，但足够多，就可能得到真正的 $f¯$。

每一个model就是一个function set，可以用上图的左下方的圈圈表示这个function set，即范围。一个简单的model的set是比较小的（可能就根本没有包含target），而上图左边的五次方方程曲线，这时的function set比较大。 虽然分布的比较散，没有办法找出target（数据少），但是比较分散在中心周围，平均起来能接近$f¯$。

3）方差VS偏差

将系列02中的误差拆分为偏差和方差。

• $Underfitting$ 欠拟合：简单模型（左边）是偏差（$bias$）比较大造成的误差
• $Overfitting$ 过拟合：复杂模型（右边）是方差（$variance$）过大造成的误差（过拟合，即在训练集表现良好，但是在测试集上很糟糕）

• 欠拟合（$bias$偏大）
  • 添加其他特征项：如组合、泛化、相关性、上下文特征、平台特征等；
  • 添加多项式特征：如线性模型添加二次型模型使得泛化能力更强；
  • 减少正则化参数：正则化是用来防止过拟合的，但现在模型欠拟合，则需要减少正则化参数。
  • 注意：如果此时强行再收集更多的data去训练，这是没有什么帮助的，因为设计的函数集本身就不好，再找更多的训练集也不会更好。
• 过拟合（$variance$偏大）
  • 重新清洗数据
  • 增加训练的数据量（如下图），可学习的特征太少，如sparrow项目的电影数据集过少，过拟合，deepFM模型参数难以收敛。
  • 使用正则化方法，使得参数越小越好（找到的曲线更平滑），也可以对$regularization$一项加上$weight$。但是正则化可能影响$bias$（曲线都平滑时可能就没包含目标的function）。
  • 使用dropout方法，在深度学习中常用（imageNet提出的）

但是很多时候不一定能做到收集更多的data。也很多种收集（调整）数据的方法，针对对问题的理解对数据集做调整。比如识别手写数字的时候，偏转角度的数据集不够，那就将正常的数据集左转15度，右转15度，类似这样的处理。

3.模型的选择

• 现在在偏差和方差之间就需要一个权衡
• 想选择的模型，可以平衡偏差和方差产生的错误，使得总错误最小

但是下面这件事最好不要做：

用训练集训练不同的模型，然后在测试集上比较错误，模型3的错误比较小，就认为模型3好。但实际上这只是你手上的测试集，真正完整的测试集并没有。比如在已有的测试集上错误是 0.5，但有条件收集到更多的测试集后通常得到的错误都是大于 0.5 的。

1）交叉验证

图中public的测试集是已有的，private是没有的，不知道的。

• 交叉验证：将训练集再分为两部分，一部分作为训练集，一部分作为验证集。用训练集训练模型，然后在验证集上比较，确定出最好的模型之后（比如模型3），再用全部的训练集训练模型3，然后再用public的测试集进行测试，此时一般得到的错误都是大一些的。
• 不过此时会比较想再回去调一下参数，调整模型，让在public的测试集上更好，但不太推荐这样。

上述方法可能会担心将训练集拆分的时候分的效果比较差怎么办，可以用下面的方法。

2）N-折交叉验证

将训练集分成N份，比如分成3份。

比如在三份中训练结果Average错误是模型1最好，再用全部训练集训练模型1。

二、Bagging与Boosting策略

• Bagging通过分而治之的策略，通过对训练样本多次采用，综合决策多个训练出来的模型，来减少集成分类器的方差。
• Boosting通过逐步聚集基分类器分错的样本，减少集成分类器的偏差。

2.1 Bagging策略

Bagging是一种并行集成方法（各基分类器之间无强依赖，可以并行训练），其全称是$\text{b}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{p}\text{ag}\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{a}\mathrm{t}\text{ing}$，即基于bootstrap抽样的聚合算法。随机森林算法就是一种基于bagging的模型，在最终决策时，每个个体单独做出判断后再进行投票作集体决策。

（1）Bootstrap抽样

• Bootstrap抽样：指从样本集合中进行有放回的抽样，假设数据集的样本容量为$n$且基学习器的个数为$M$，对于每个基学习器我们可以进行有放回地抽取$n$个样本，从而生成了$M$组新的数据集，每个基学习器分别在这些数据集上进行训练，再将最终的结果汇总输出。

• 那这样的抽样方法有什么好处呢？

  • 数据集是从总体分布$p(\text{X})$中抽样得到的，此时数据集构成了样本的经验分布$\tilde{p}(\text{X})$，由于采用了有放回抽样，因此$M$个数据集中的每一组新样本都来自于经验分布$\tilde{p}(\text{X})$。
  • 同时由大数定律知，当样本量$n\to \infty$时，经验分布$\tilde{p}(\text{X})$收敛到总体分布$p(\text{X})$，因此大样本下的新数据集近似地抽样自总体分布$p(\text{X})$。

假设我们处理的是回归任务，并且每个基学习器输出值$y^{(i)}$的方差为${\sigma }^2$，基学习器两两之间的相关系数为$\rho$，则可以计算集成模型输出的方差为

$$\begin{array}{rl}Var(\hat{y})& =Var(\frac{{\sum }_{i=1}^M{y}^{(i)}}{M})\\ & =\frac{1}{M^2}[\sum _{i=1}^{M}Var(y^{(i)})+\sum _{i\ne j}Cov(y^{(i)},y^{(j)})]\\ & =\frac{1}{M^2}[M{\sigma }^2+M(M-1)\rho {\sigma }^2]\\ & =\rho {\sigma }^2+(1-\rho )\frac{{\sigma }^2}{M}\end{array}$$

从上式的结果来看，当基模型之间的相关系数为1时方差不变，这相当于模型之间的输出完全一致，必然不可能带来方差的降低。

bootstrap的放回抽样特性保证了模型两两之间很可能有一些样本不会同时包含，这使模型的相关系数得以降低，而集成的方差随着模型相关性的降低而减小，如果想要进一步减少模型之间的相关性，那么就需要对基学习器进行进一步的设计。

（2）bootstrap造成的数据集差异

为了更具体地了解bootstrap造成的数据集差异，我们往往对两个量是非常关心的，它们分别是单个样本的入选概率和入选（非重复）样本的期望个数。我们首先计算第一个量：对于样本容量为$n$的原数据集，抽到某一个给定样本的概率是$\frac{1}{n}$，进行$n$次bootstrap采样但却没有选入该样本的概率为$(1-\frac{1}{n}{)}^n$，从而该样本入选数据集的概率为$$1-(1-\frac{1}{n}{)}^n$$，当$n\to \infty$时的概率为$1-e^{-1}$。对于第二个量而言，记样本$i$在$n$次抽样中至少有一次入选这一事件为$A_i$，那么非重复样本的个数为 ∑ i = 1 n 1 { A i } \sum_{i=1}^n\mathbb{1}_{\{A_i\}} i=1∑n​1{ Ai​}​ 从而期望个数为

E ∑ i = 1 n 1 { A i } = ∑ i = 1 n E 1 { A i } = ∑ i = 1 n P ( A i ) = ∑ i = 1 n 1 − ( 1 − 1 n ) n = n [ 1 − ( 1 − 1 n ) n ] \begin{aligned} \mathbb{E}\sum_{i=1}^n\mathbb{1}_{\{A_i\}} &= \sum_{i=1}^n\mathbb{E}\mathbb{1}_{\{A_i\}} \\ &= \sum_{i=1}^nP(A_i)\\ &= \sum_{i=1}^n 1-(1-\frac{1}{n})^n\\ &= n[1-(1-\frac{1}{n})^n] \end{aligned} Ei=1∑n​1{ Ai​}​​=i=1∑n​E1{ Ai​}​=i=1∑n​P(Ai​)=i=1∑n​1−(1−n1​)n=n[1−(1−n1​)n]​

若$n\to \infty$时，入选样本占原数据集的期望比例为
lim ⁡ n → ∞ E ∑ i = 1 n 1 { A i } n = lim ⁡ n → ∞ [ 1 − ( 1 − 1 n ) n ] \displaystyle \lim_{n\to \infty}\frac{\mathbb{E}\sum_{i=1}^n\mathbb{1}_{\{A_i\}}}{n}=\lim_{n\to\infty} [1-(1-\frac{1}{n})^n] n→∞lim​nE∑i=1n​1{ Ai​}​​=n→∞lim​[1−(1−n1​)n]即$1-e^{-1}$。

2.2 Boosting

Boosting是一种串行集成方法（迭代式学习），各个基分类器之间有依赖。每层在训练时，对前一层基分类器分错的样本，给予更高的权重。

假设第$i$个基模型的输出是$${\hat{f}}^{(i)}(\mathbf{X})$$ 则总体模型的输出为${\sum }_{i=1}^M{\alpha }_i{\hat{f}}^{(i)}(\tilde{X})$。boosting算法在拟合第$T$个学习器时，已经获得了前$T-1$个学习器的集成输出
$$\sum _{i=1}^{T-1}{\alpha }_i{\hat{f}}^{(i)}(\mathbf{X})$$

对于损失函数$L(y,\hat{y})$，当前轮需要优化的目标即为使得
$$L(y,{\alpha }_T{\hat{f}}^{(T)}(\mathbf{X})+\sum _{i=1}^{T-1}{\alpha }_i{\hat{f}}^{(i)}(\mathbf{X}))$$

最小化。注意：当前轮所有需要优化的参数一般而言都会蕴藏在${\alpha }_T{\hat{f}}^{(T)}$这一项中，不同的模型会对$${\alpha }_T{\hat{f}}^{(T)}$$提出的不同假设。此外，由于优化损失在经验分布与总体分布相差不多的时候等价于优化了模型的偏差，因此多个模型集成后相较于单个模型的预测能够使得偏差降低。

Boosting的过程很类似于人类学习的过程，我们学习新知识的过 程往往是迭代式的，第一遍学习的时候，我们会记住一部分知识，但往往也会犯 一些错误，对于这些错误，我们的印象会很深。第二遍学习的时候，就会针对犯 过错误的知识加强学习，以减少类似的错误发生。不断循环往复，直到犯错误的 次数减少到很低的程度。

2.3 基分类器用树型模型的原因

集成学习一般三部曲的第一步是【找到误差互相独立的基分类器】，事实上，任何 分类模型都可以作为基分类器，但树形模型由于结构简单且较易产生随机性所以比较常用。具体的3点原因：

• 决策树可以较为方便地将样本的权重整合到训练过程中，而不需要使用 过采样的方法来调整样本权重。
• 决策树的表达能力和泛化能力，可以通过调节树的层数来做折中。
• 数据样本的扰动对于决策树的影响较大，因此不同子样本集合生成的决 策树基分类器随机性较大，这样的“不稳定学习器”更适合作为基分类器。此外， 在决策树节点分裂的时候，随机地选择一个特征子集，从中找出最优分裂属性， 很好地引入了随机性。 除了决策树外，神经网络模型也适合作为基分类器，主要由于神经网络模型 也比较“不稳定”，而且还可以通过调整神经元数量、连接方式、网络层数、初始 权值等方式引入随机性。

Reference

[1] 沐神机器学习课程
[2] https://c.d2l.ai/stanford-cs329p/