题目
题目描述
** 原题来自:SCOI 2009**
Windy 在有向图中迷路了. 该有向图有 n n n个节点,Windy 从节点 0 0 0 出发,他必须恰好在 T T T时刻到达节点 N − 1 N-1 N−1。
现在给出该有向图,你能告诉 Windy 总共有多少种不同的路径吗?
注意:Windy 不能在某个节点逗留,且通过某有向边的时间严格为给定的时间。
输入格式
第一行包含两个整数 N N N, T T T;
接下来有 N N N行,每行一个长度为 N N N的字符串。第 i i i行第 j j j列为 0表示从节点 i i i到节点 j j j没有边,为 1 1 1到 9 9 9表示从节点 i i i节点 j j j需要耗费的时间。
输出格式
包含一个整数,可能的路径数,这个数可能很大,只需输出这个数除以 2009 2009 2009的余数。
样例
样例输入 1
2 2
11
00
样例输出 1
1
样例输入 2
5 30
12045
07105
47805
12024
12345
样例输出 2
852
数据范围和提示:
2 <= N <= 10 ; 1 <= T <= 1000000000 ;0<=边权<=9;
题解
第一反应:咦?这不是图论吗???
默默的看了眼T的范围,死了心
DP!! DP一定可以!!!
默默的看了眼T的范围,又死了心
那么怎么做呢?
第一部分
首先,我们把这道题想简单一点,如果题目中的每一条边都没有边权,只用1或0来表示两个点之间是否存在边,并且用邻接矩阵来存这张图,那么我们又可以得到些什么呢?
举个栗子
我们以下面这张图为例

以邻接矩阵来表示这个矩阵:
0 1 1
1 0 1
1 0 0 //矩阵1
其中,aij表示i到j之间是否有连线;
那么,我们把它平方一下,又可以得到什么呢?(友情提示:如果不清楚矩阵乘法,请点这里)
2 0 1
1 1 1
0 1 1 //矩阵2
你又发现了什么呢?
好的,如果还没发现,我们再来将矩阵1三次方一下:
1 2 2
2 1 2
2 0 1 //矩阵3
什么,你还没发现吗???
那么让我来告诉你吧!!!
仔细观察矩阵1,我们可以把aij看成通过一条边,由i到达j的情况总数
矩阵2、矩阵3也是如此;
不信?我们举个栗子:
从点1到点2,且通过一条边的情况不存在,记为0;
从点1到点2,且通过两条边的情况共两种(1->2->1 and 1->3->1),记为2;
从点1到点2,且通过三条边的情况仅有一种(1->2->3->1),记为1;
再回头看看矩阵吧!!!是不是完全满足这个条件呢???
所以我们就可以得出结论啦:
在矩阵Ax中,Axij表示由i到j经过x条边的情况总数
所以这就可以运用快速幂啦!!!
仔细算一下时间复杂度,O(n*logn),稳稳滴!!!
那么,这道题就可以很快打出来啦——吗?
显然是不可以的。
可能你已经发现了,我们所有的推论都建立在边权为1的情况上,可是这道题目呢?
接下来有 N N N行,每行一个长度为 N N N的字符串。第 i i i行第 j j j列为 0表示从节点 i i i到节点 j j j没有边,为 1 1 1到 9 9 9表示从节点 i i i到节点 j j j需要耗费的时间。
呀呀呀,这道题目的边权不只是1呀!
!(⊙ o ⊙)!
怎么办呢?
第二部分
虽然我们发现不能直接使用我们的结论,但是最大边权是9!N也不超过10!都不算大!
那我们就可以采用一种叫做拆点的方法:把一个点拆成10个点。
并且,我们发现即使如此拆点,N也不会超过100,妥妥的可以呀!
但怎么拆点呢?
我们先来试一下拆一个边权不超过2的图吧!

可得矩阵
0 2
2 1
将其拆点:

把1.1看成节点1;
把1.2看成节点2;
把2.1看成节点3;
把2.2看成节点4;
可得到新矩阵 :
0 1 0 0
0 0 1 0
0 0 1 1
1 0 0 0
将其平方:
0 0 1 0
0 0 1 1
1 0 1 1
0 1 0 0
再验算一下,
原来有点1到点2并用经过2边权的方案总数有一种(1->2,边权为2);
现在来说,点1变为点1,点2变为点3,经过2边权的方案总数依旧是2(1->2->3,边权均为1);
那么则说明我们的拆点是正确的。
那么怎么做呢?
我们再对非零点进行分类,原先就有的1看成蓝色,后面通过自连得到的1看成红色:
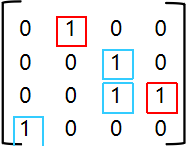
那么下面的代码就可以进行拆点操作:
int Cheak(int i,int j){
return (i-1)*10+j;
}
void ChaiDian(){
for(int i=1;i<=N;i++){
for(int j=1;j<Maxn;j++){
//Maxn表示最大边权
f[Cheak(i,j)][Cheak(i,j+1)]=1; //对红点标记
}
for(int j=1;j<=N;j++){
if(a[i][j]){
//对本来就存在的点进行标记
f[Cheak(i,a[i][j])][Cheak(j,1)]=1;
}
}
}
}
那么既然我们通过拆点操作将所有点之间的边权都变成了1,那么我们就可以用刚才得到的定理啦!!!
代码
#include<bits/stdc++.h>
using namespace std;
int n,t;
const long long Mod=2009;
struct Matrix {
int Ma[205][205];
void clear(){
memset(Ma,0,sizeof Ma);
}
}A;
Matrix YunSuan(Matrix x, Matrix y) {
//乘法
Matrix now;
now.clear();
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= n; k++) {
now.Ma[i][j]=(now.Ma[i][j]+x.Ma[i][k] * y.Ma[k][j])%Mod;
}
}
}
return now;
}
Matrix Power(Matrix a,int b){
//快速幂
Matrix now;
now.clear();
for(int i=1;i<=n;i++){
now.Ma[i][i]=1;
}
while(b){
if(b&1)
now=YunSuan(now,a);
a=YunSuan(a,a);
b>>=1;
}
return now;
}
int Cheak(int i,int j){
return (i-1)*10+j;
}
int main(){
scanf("%d%d",&n,&t);
int N=n;
n*=10;
for(int i=1;i<=N;i++){
for(int j=1;j<10;j++){
A.Ma[Cheak(i,j)][Cheak(i,j+1)]=1;
}
for(int j=1;j<=N;j++){
int x;
scanf("%1d",&x);
if(x){
A.Ma[Cheak(i,x)][Cheak(j,1)]=1;
}
}
}
A=Power(A,t);
printf("%d\n",A.Ma[1][10*N-9]);
}