Сегодня я расскажу о трех алгоритмах, которые имеют высокую частоту и которые легко спутать: это подмножество, перестановка и комбинация. Эти проблемы могут быть решены с помощью алгоритма возврата.
1. Проблема подмножества
очень проста: введите массив, который не содержит повторяющихся чисел, и попросите алгоритм вывести все подмножества этих чисел.
vector <vector < int >> subsets (vector < int > & nums);
Например, введите nums = [1,2,3], ваш алгоритм должен вывести 8 подмножеств, включая пустой набор и сам по себе, порядок может быть другим:
[[], [1], [2], [3], [1,3], [2,3], [1,2], [1,2,3]]
Первое решение состоит в том, чтобы использовать идею математической индукции: предположим, теперь я знаю результаты небольшой подзадачи, как я могу получить результаты текущей задачи?
В частности, позвольте мне спросить вас о подмножестве [1,2,3]. Если вы знаете подмножество [1,2], можете ли вы вывести подмножество [1,2,3]? Сначала запишите подмножество [1,2] и посмотрите:
[[], [1], [2], [1,2]]
Вы найдете такое правило:
подмножество ([1,2,3]) - подмножество ([1,2])
= [3], [1,3], [2,3], [1,2,3]
И этот результат заключается в добавлении 3 к каждому набору в результате sebset ([1,2]).
Другими словами, если A = подмножество ([1,2]), то:
Подмножество ([1,2,3])
= A + [A [i] .add (3) для i = 1..len (A)]
Это типичная рекурсивная структура: подмножество [1,2,3] может быть добавлено с помощью [1,2], подмножество [1,2] может быть добавлено с помощью [1], базовый случай, очевидно, То есть, когда входной набор является пустым набором, выходной поднабор также является пустым набором.
В переводе на код это легко понять:
vector <vector < int >> subsets (vector < int > & nums) { // базовый случай, вернуть пустой набор if (nums.empty ()) return {{}}; // вынуть последний элемент из int n = nums.back (); nums.pop_back (); // Рекурсивный расчет всех подмножеств предыдущих элементов vector <vector < int >> res = subsets (nums); int size = res.size (); for ( int i = 0 ; i <size; i ++ ) { // Затем добавьте res.push_back (res [i]); res.back (). push_back (n); } returnРез; }
Расчет временной сложности этой задачи сравнительно прост. Метод, который мы использовали для вычисления временной сложности рекурсивного алгоритма, состоит в том, чтобы найти глубину рекурсии и затем умножить ее на количество итераций в каждой рекурсии. Для этой задачи глубина рекурсии, очевидно, равна N, но мы обнаружили, что число итераций каждой рекурсивной последовательности цикла зависит от длины res и не является фиксированной.
Согласно идее только сейчас, длина res должна удваиваться в каждой рекурсии, поэтому общее число итераций должно быть 2 ^ N. Или без таких хлопот, как вы думаете, сколько подмножеств из набора размера N? 2 ^ N верно, так что, по крайней мере, добавьте 2 ^ N элементов в res.
Так является ли временная сложность алгоритма O (2 ^ N)? Все еще не правильно, 2 ^ N подмножества добавляются push_back к res, поэтому следует рассмотреть эффективность операции push_back:
vector <vector < int >> res = ... for ( int i = 0 ; i <size; i ++ ) { res.push_back (res [i]); // O (N) res.back (). Push_back (n); // O (1) }
Поскольку res [i] также является массивом, push_back копирует копию res [i] и добавляет ее в конец массива, поэтому время одной операции равно O (N).
Таким образом, общая сложность времени составляет O (N * 2 ^ N), что довольно много времени.
Для сложности пространства, если вы не вычисляете пространство, используемое для хранения возвращаемого результата, требуется только O (N) рекурсивное пространство стека. Если рассчитывается пространство, необходимое для res, оно должно быть O (N * 2 ^ N).
Второй общий метод - алгоритм возврата. Старый алгоритм возврата текста подробно объяснил шаблон алгоритма возврата:
result = [] def backtrack (путь, список выбора): если выполнено условие конца: result.add (путь) возврат для выбора в списке выбора: сделать выбор возврата (путь, список выбора), чтобы отменить выбор
Просто измените шаблон алгоритма возврата:
vector <vector < int >> res; vector <vector < int >> subsets (vector < int > & nums) { // Записать пройденный путь вектора < int > track; backtrack (nums, 0 , track); вернуть res ; } void backtrack (vector < int > & nums, int start, vector < int > & track) { res.push_back (track); // Обратите внимание, что i увеличивается с начала для ( int i = start; i <nums.size) (); i ++ ) { // сделать выбор track.push_back (nums [i]); // возвращение назад (nums, i + 1 , track); // отмена выбора track.pop_back (); } }
Как видите, обновление до res - это обход по предварительному заказу, то есть res - это все узлы в дереве:

2. Объедините
два числа n, k, и алгоритм выведет все комбинации чисел k в [1..n].
vector <vector <int >> объединить (int n, int k);
например, при вводе n = 4, k = 2 вывести следующие результаты, порядок не имеет значения, но не может содержать повторение (согласно определению комбинации [1,2] и [ 2,1] также повторяется):
[
[1,2],
[1,3],
[1,4],
[2,3],
[2,4],
[3,4]
]
Это типичный алгоритм обратного отслеживания. K ограничивает высоту дерева, а n ограничивает ширину дерева. Просто примените шаблонную структуру алгоритма обратного отслеживания, о котором мы говорили ранее:
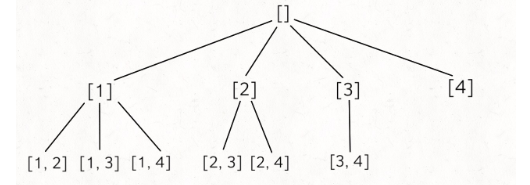
vector <vector < int >> res; vector <vector < int >> объединить ( int n, int k) { if (k <= 0 || n <= 0 ) return res; vector < int > track; возвратный путь (n, k, 1 , трек); вернуть Res; } void backtrack ( int n, int k, int start, vector < int > & track) { // 到达 树 的 底部 if (k ==track.size ()) { res.push_back (track); return ; } // Обратите внимание, что i увеличивается от начала для ( int i = start; i <= n; i ++ ) { // сделать выбор track.push_back (i) ; BackTrack (н-, K, I + 1. , дорожка); // Отмена выбора track.pop_back (); } }
Функция возврата обратно похожа на подмножество вычислений, разница в том, что место для обновления res - это нижняя часть дерева.
3. Перестановка
Введите номер массива, который не содержит повторяющихся чисел, и верните все перестановки этих чисел.
vector <vector <int >> permute (vector <int> & nums);
например, входной массив [1,2,3], выходной результат должен быть следующим, порядок не имеет значения, повторений не может быть:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
В подробном объяснении алгоритма обратного отслеживания эта проблема используется для объяснения шаблона обратного отслеживания. Здесь также указана эта проблема, которая заключается в сравнении кодов двух алгоритмов возврата: «расположение» и «сочетание».
Сначала нарисуйте дерево трассировки, чтобы посмотреть:
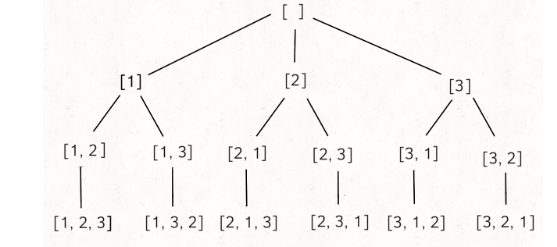
Мы использовали код Java для написания решения:
List <List <Integer >> res = new LinkedList <> (); / * Основная функция, введите группу неповторяющихся чисел и вернет их полное расположение * / List <List <Integer >> permute ( int [] nums) { // Записать «путь» LinkedList <Integer> track = new LinkedList <> (); возврат назад (nums, track); return res; } void backtrack ( int [] nums, LinkedList <Integer> track) { // Конец триггера Условный if (track.size () == nums.length) { res.add ( новый LinkedList (track)); return ; } для( int i = 0 ; i <nums.length; i ++ ) { // Исключить недопустимые варианты, если (track.contains (nums [i])) continue ; // Сделать выбор track.add (nums [i]); // Вход на следующий уровень дерева решений backtrack (nums, track); // Отмена выбора track.removeLast (); } }
Шаблон обратного отслеживания не изменился, но в соответствии с деревом, построенным задачей перестановки и проблемой объединения, дерево задачи перестановки является более симметричным, и чем ближе дерево к проблеме объединения, тем меньше правильных узлов.
Проявление в коде состоит в том, что проблема компоновки использует метод содержимого для исключения чисел, которые были выбраны в дорожке каждый раз, и проблема комбинирования переходит в параметр запуска, чтобы исключить число перед начальным индексом.
Выше приведено решение трех проблем перестановки, комбинации и подмножества.
Задача подмножества может использовать идею математической индукции, предполагая, что результаты меньшей задачи известны, и как получить результаты исходной задачи. Вы также можете использовать алгоритм возврата, используя параметр start для исключения выбранных номеров.
В задаче объединения используется идея обратного отслеживания, и результат может быть выражен в виде древовидной структуры. Нам нужно только применить шаблон алгоритма обратного отслеживания. Ключевым моментом является использование начала, чтобы исключить выбранные числа.
Проблема размещения - это ретроспективная идея, и она также может быть выражена в виде древовидной структуры для применения шаблона алгоритма. Ключевым моментом является использование метода содержимого для исключения выбранных чисел. Предыдущая статья содержит подробный анализ. Здесь в основном проводится сравнение с проблемой объединения.
Для этих трех задач вы можете понять смысл кода, наблюдая за структурой рекурсивного дерева. ,