Aprendendo Algoritmos e Aplicações de Modelagem Matemática 【Análise de Regressão】

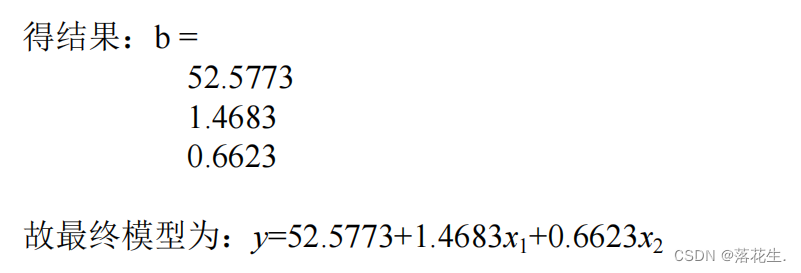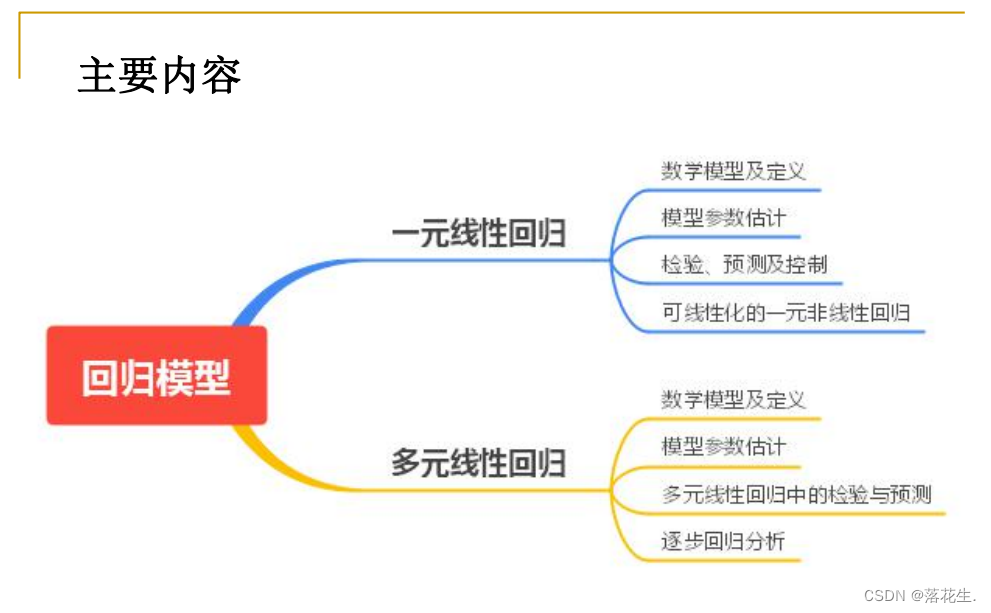
A primeira metade é conhecimento básico, a segunda metade é análise de exemplos e prática de MATLAB

Regressão linear univariada

Modelos matemáticos e definições

Em outras palavras, trata-se de minimizar a soma dos quadrados das distâncias verticais de todos os pontos amostrais até a linha de regressão amostral.

Estimativa de parâmetros do modelo

Inspeção, previsão e controle

Regressão não linear univariada linearizável

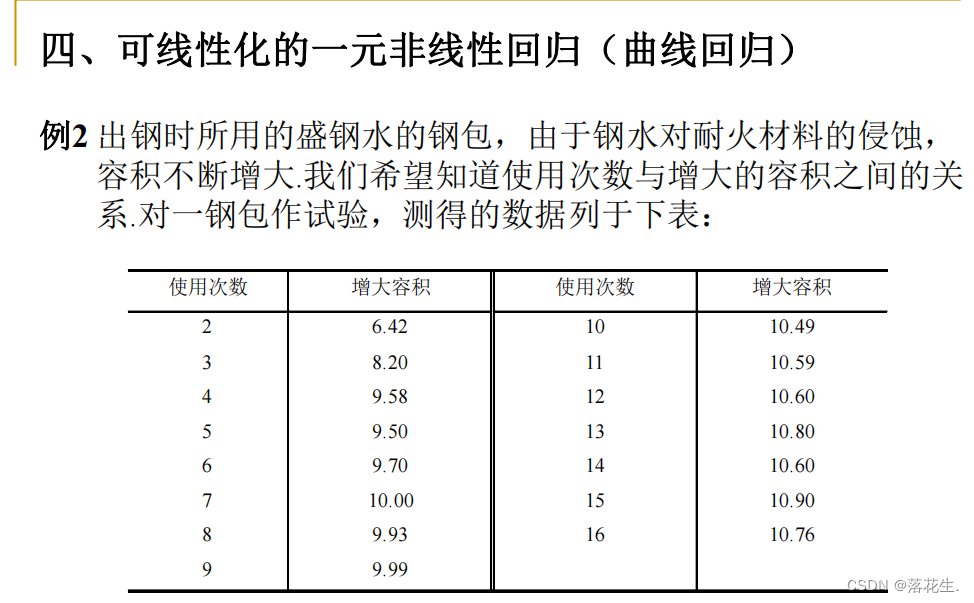
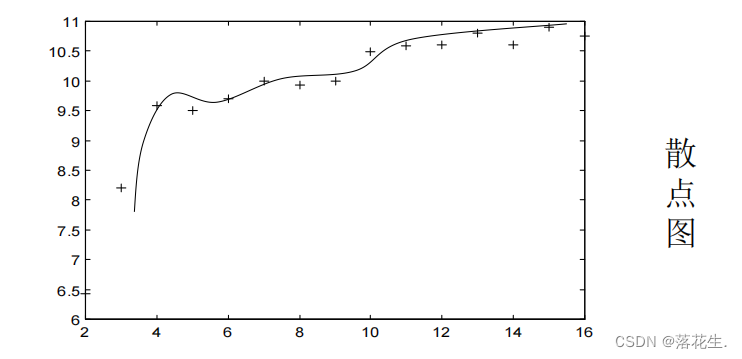
Este é um problema de regressão não linear ou regressão de curva (uma curva precisa ser correspondida).O
método geral de correspondência de uma curva é:
primeiro conduza n testes em duas variáveis ​​​​x e y e observe (x;, y;), i = 12 ,...,n Desenhe um diagrama de dispersão e determine o tipo de curva a ser correspondida com base no diagrama de dispersão. Em seguida, determine os parâmetros desconhecidos e b de cada tipo de curva a partir de n pares de dados de teste. O método usado é converter regressão não linear em regressão linear por meio de substituição de variável, ou seja, O método de regressão não linear e linearização é usado.

A diferença entre análise de correlação e análise de regressão
é analisar se existe uma correlação e qual é o grau de correlação; a análise de regressão é construir variáveis ​​de tabela e fórmulas funcionais específicas entre variáveis ​​e usar funções ou equações para ajustá-las.
Nível de significância: estima a probabilidade geral de cometer um erro quando o parâmetro geral está dentro de um determinado intervalo, geralmente 5%

Regressão linear múltipla

Análise de comando de regressão e exemplos
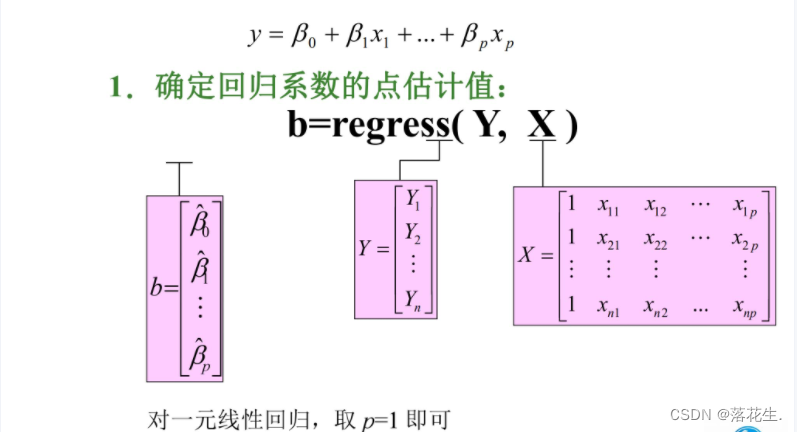
1. Regressão linear múltipla
2. Regressão polinomial
3. Regressão não linear
4. Regressão passo a passo

1. Modelos matemáticos e definições

2. Estimativa de parâmetros do modelo

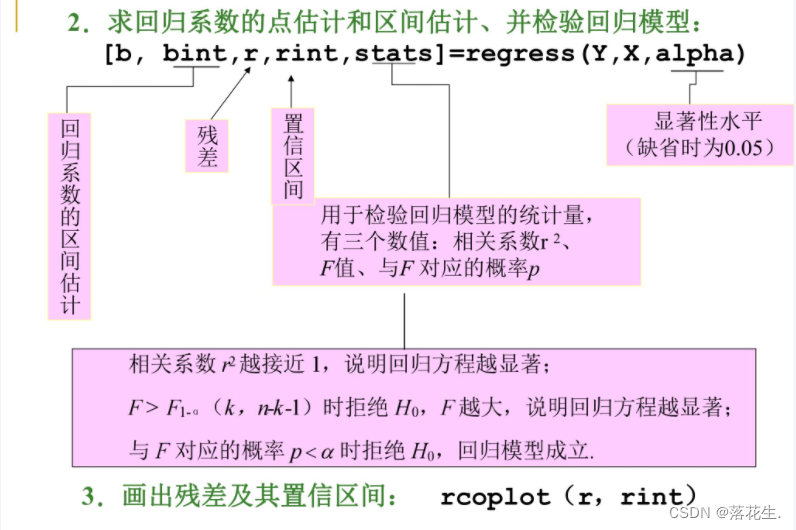
3. Teste e previsão em regressão linear múltipla

4. Análise de regressão passo a passo

A equação de regressão "ótima" é uma equação de regressão que inclui todas as variáveis ​​que têm impacto em Y, excluindo
variáveis ​​que têm um impacto insignificante em Y. Existem várias maneiras de selecionar a equação de regressão "ótima":
(1) De todas as variáveis Selecione o ideal da equação de regressão de possíveis combinações de fatores (variáveis);
(2) Elimine os fatores não significativos um por um da equação de regressão contendo todas as variáveis;
(3) Comece com uma variável e introduza as variáveis ​​na equação um por um;
(4)) análise de regressão passo a passo "dentro e fora". O quarto método, análise de regressão passo a passo, é mais ideal na triagem de variáveis
.

A ideia do método de análise de regressão stepwise
: • Partindo de uma variável independente, dependendo da significância da variável independente Y, introduza a equação de regressão uma por uma
, de pequena. • Quando a variável independente introduzida se torna devido ao introdução de variáveis ​​subsequentes Quando não for significativo,
deve ser eliminado. • A introdução de uma variável independente ou a remoção de uma variável independente da equação de regressão é um
passo na regressão stepwise. • Um teste de valor Y deve ser realizado para cada passo para garantir que cada sempre que uma nova variável é introduzida A equação de regressão antes das
variáveis ​​significativas inclui apenas variáveis ​​que têm um efeito significativo em Y. • Este processo é repetido até que nenhuma variável insignificante seja removida da equação de regressão e nenhuma variável significativa possa ser introduzida na equação de regressão
.

Regressão linear múltipla

Código de resposta

%输入数据
x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';
X=[ones(16,1) x];
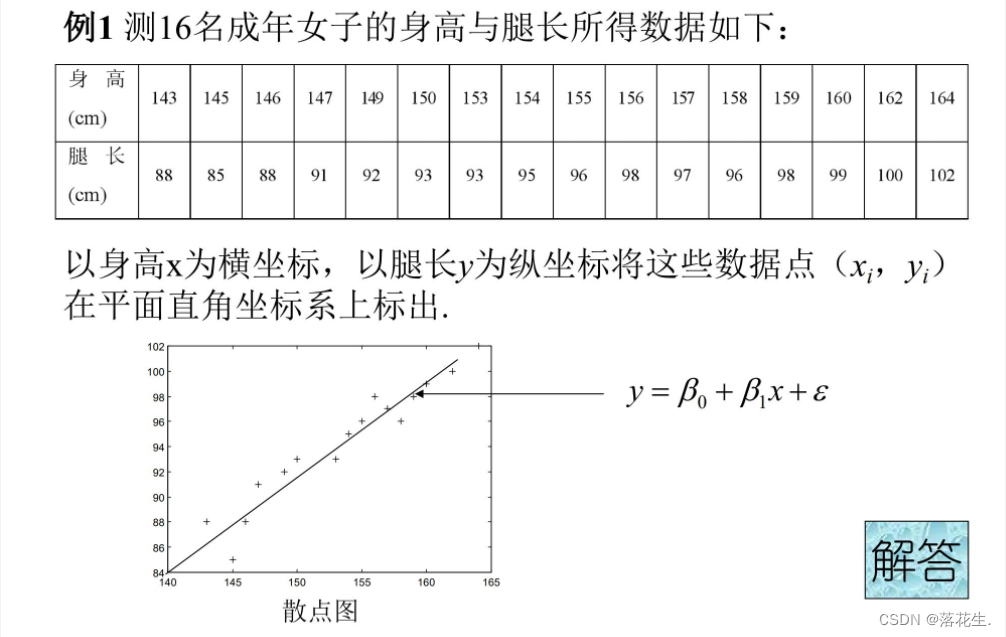
Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';
%回归分析与检验
[b,bint,r,rint,stats]=regress(Y,X)
rcoplot(r,rint)%做残差图
%图像的预测与对比
z=b(1)+b(2)*5%这里乘几都可以，只是为了做个对比。
plot(x,Y,'k+',x,z,'r')

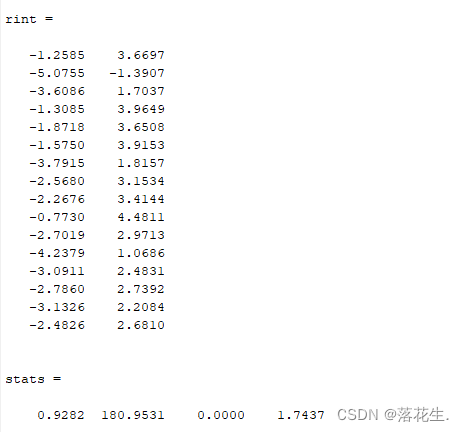
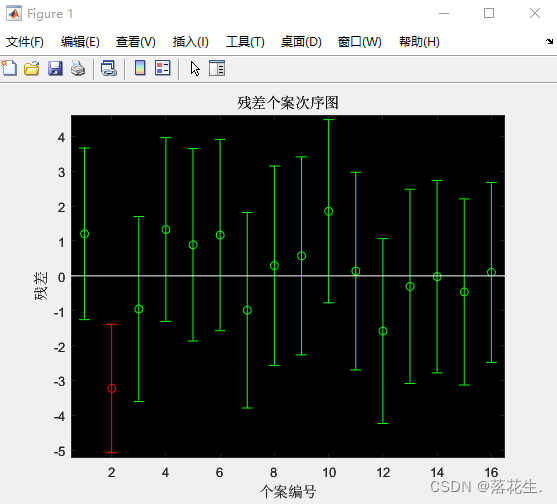
Pode-se observar no gráfico de resíduos que, exceto para os segundos dados, os resíduos do restante dos dados são próximos de zero, e todos os intervalos de confiança dos resíduos incluem zero, o que mostra que o modelo de regressão y-16.073+ 0,7194x pode funcionar melhor de forma consistente com os dados originais, enquanto os segundos dados podem ser considerados discrepantes.

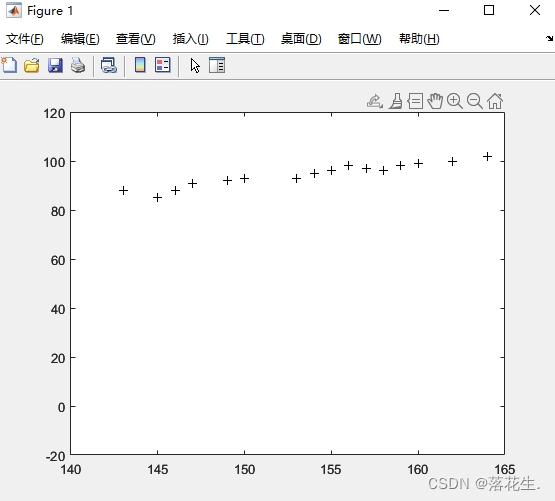
regressão polinomial

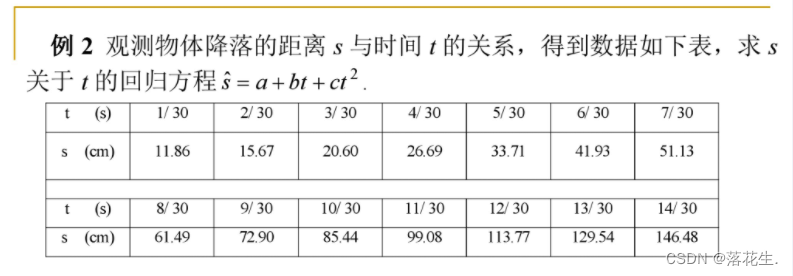
Faça a regressão polinomial quadrática diretamente:

t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49  72.90 85.44 99.08 113.77 129.54 146.48];
[p,S]=polyfit(t,s,2)%2指的是最高次数为2次

Resultados da execução


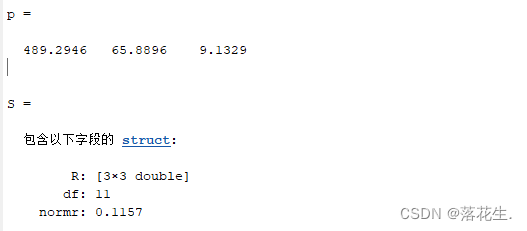
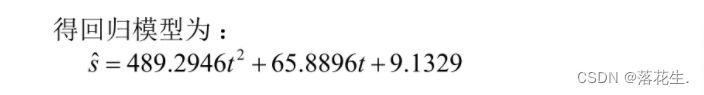
O segundo método: pode ser convertido em regressão linear múltipla.Trate
t ² como um elemento, ou seja, x2, e assim se torna uma regressão linear múltipla para cálculo.

%多项式回归化为多元线性回归
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
T=[ones(14,1) t' (t.^2)'];%为14*3的矩阵
[b,bint,r,rint,stats]=regress(s',T);%回归系数，回归系数的区间估计，残差，置信期间
b,stats%回复系数和检验回归模型的统计量
%预测及作图
Y=polyconf(p,t,S)%求回归多项式在x处的预测值Y
plot(t,s,'k+',t,Y,'r')

resultado da operação

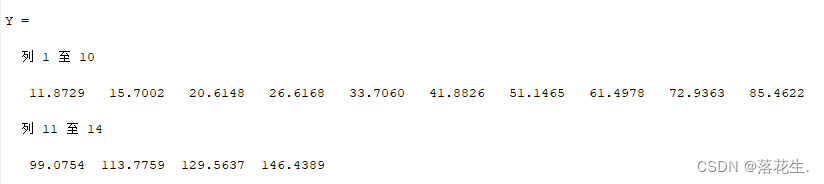
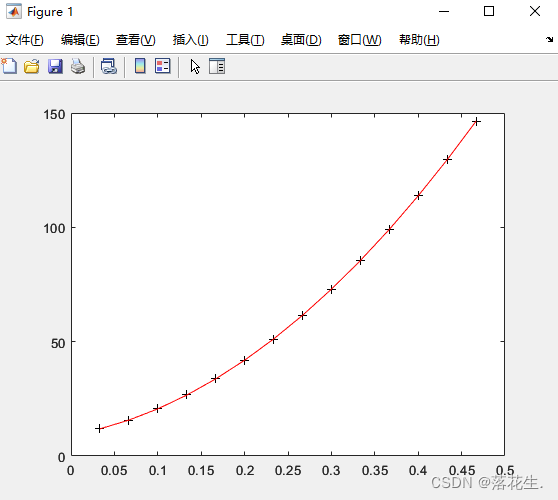
Regressão Binomial Múltipla

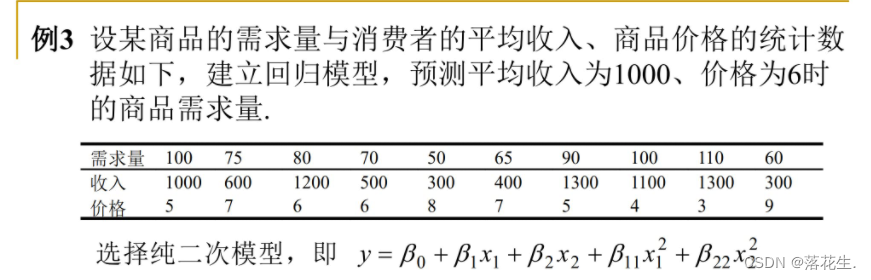
O Método 1
usa diretamente
código de regressão binomial multivariada

x1=[1000 600 1200 500 300 400 1300 1100 1300 300];
x2=[5 7 6 6 8 7 5 4 3 9];
y=[100 75 80 70 50 65 90 100 110 60]';
x=[x1' x2'];
rstool(x,y,'purequadratic')%多元二项式回归，纯二次型

Os valores em x1 e x2 dos resultados em execução

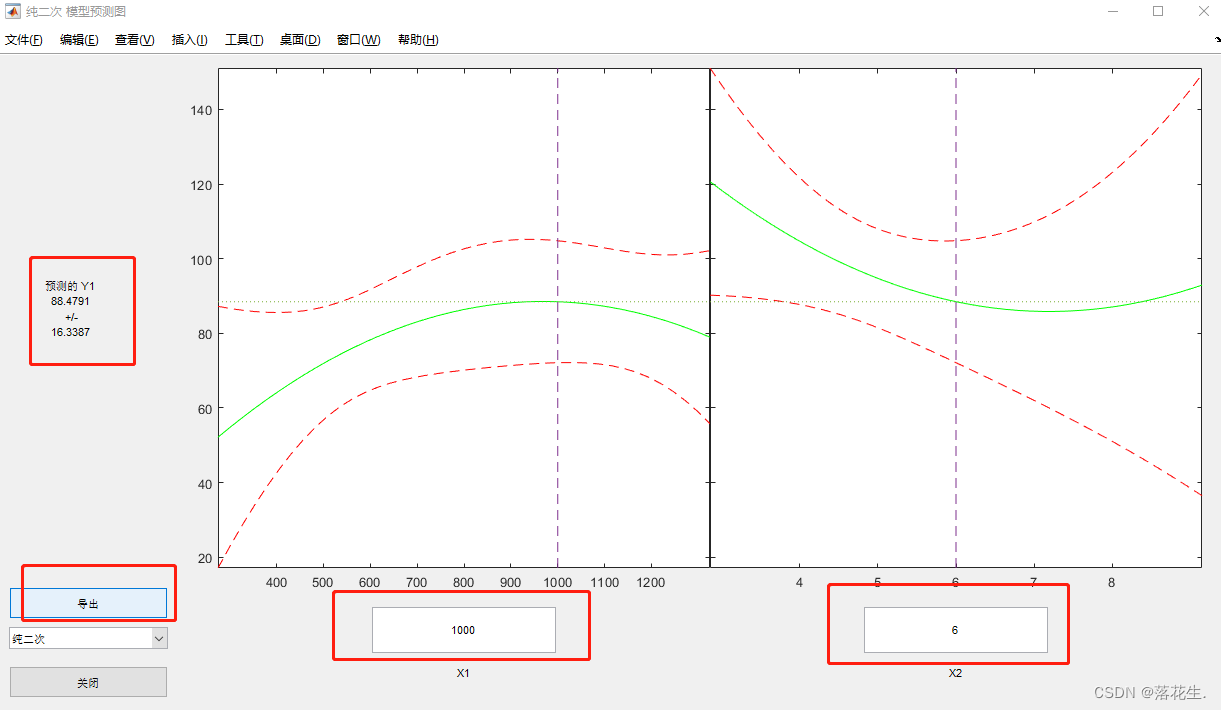
precisam ser alterados manualmente por você mesmo. Basta alterá-los para os valores necessários. Os
resultados da previsão serão exibidos à esquerda
. Clique em saída para beta. Tanto o rmse quanto os resíduos são transferidos para o espaço de trabalho do MATLAB.



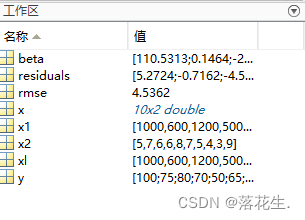
Geralmente, o rmse é menor que 10.
Método 2:
Converter forma quadrática pura em
código de regressão linear múltipla

%多元二项式化为多元线性回归
x1=[1000 600 1200 500 300 400 1300 1100 1300 300];
x2=[5 7 6 6 8 7 5 4 3 9];
y=[100 75 80 70 50 65 90 100 110 60]';
x=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)'];
[b,bint,r,rint,stats]=regress(y,x);
b,stats

resultado da operação

regressão não linear

Exemplo Primeiro, crie o código volum.m do arquivo M para o modelo não linear y=ae ^b/x

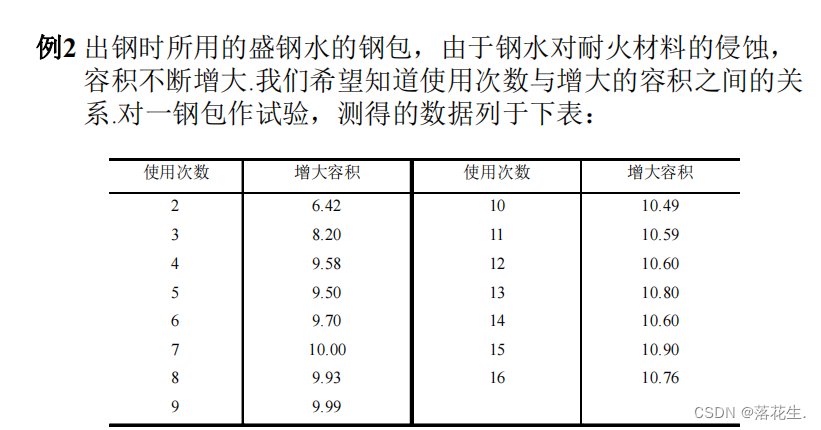
a ser ajustado

%非线性拟合
        %对将要拟合的非线性模型y=ae^b/x,建立M文件volum.m
        %function yhat=volum(beta,x)
        % yhat=beta(1)*exp(beta(2)./x);
%输入数据
x=2:16;
y=[6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76];
beta0=[8 2]';%初值
%求回归系数
[beta,r ,J]=nlinfit(x',y','volum',beta0);
beta

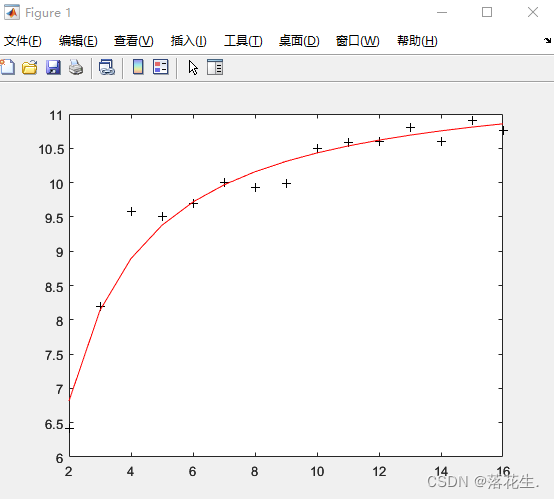
O resultado da operação

é que o modelo de regressão é: y
=11,6036e ^-1,0641/x

regressão gradual

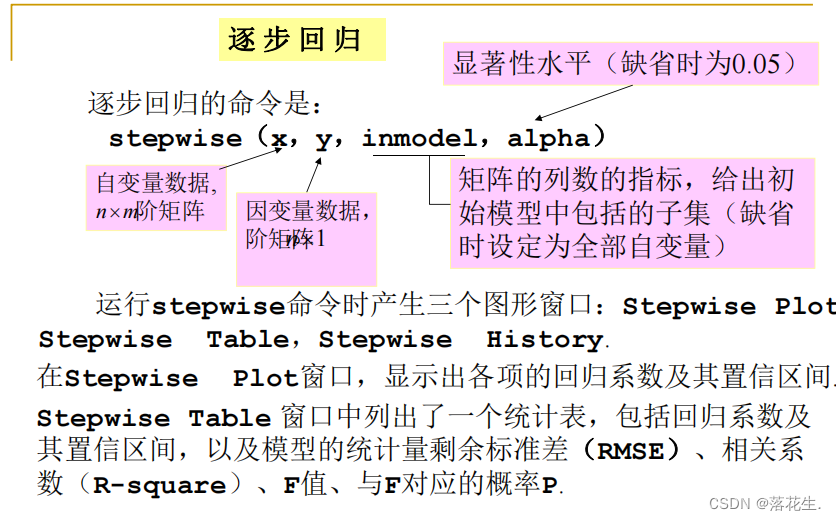
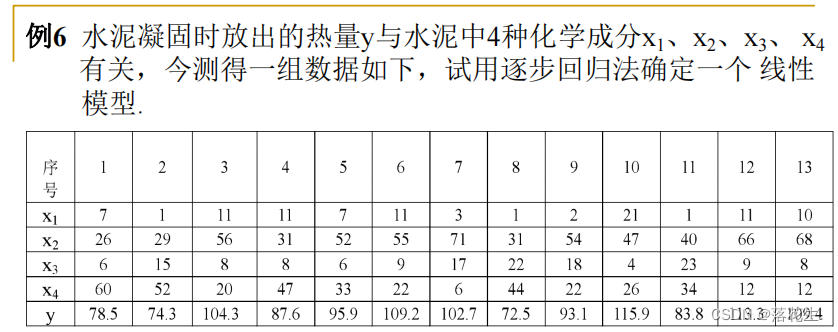
código

x1=[7 1 11 11 7 11 3 1 2 21 1 11 10]';
x2=[26 29 56 31 52 55 71 31 54 47 40 66 68]';
x3=[6 15 8 8 6 9 17 22 18 4 23 9 8]';
x4=[60 52 20 47 33 22 6 44 22 26 34 12 12]';
y=[78.5 74.3 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.8 113.3 109.4]';
x=[x1 x2 x3 x4];
stepwise(x,y)

Clique em Avançar para executar os resultados

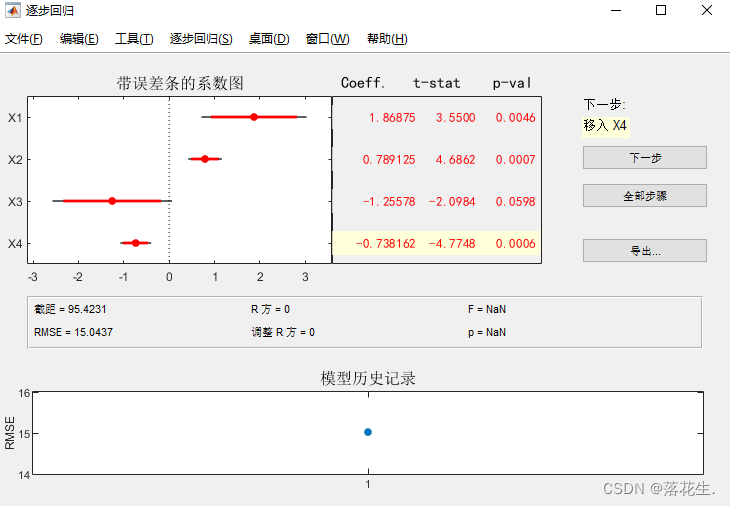
, mova gradualmente cada variável e observe as mudanças em cada indicador até encontrar a combinação mais adequada de variáveis ​​independentes. Clique em Avançar, ou seja, mova os
resultados da observação x4.

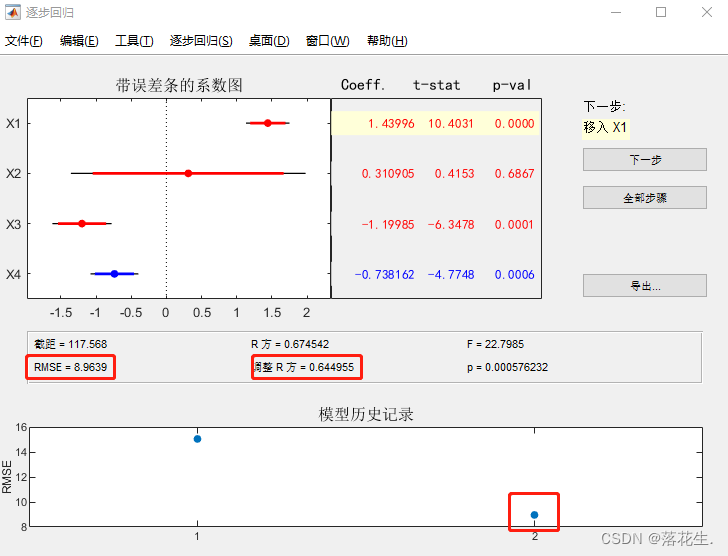
Continue clicando em Avançar, que isto é, mova os resultados da observação x1 e

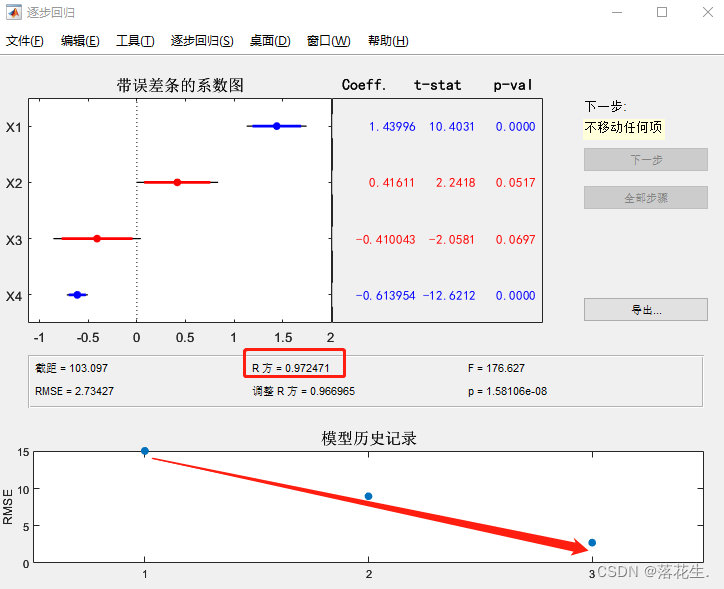
você poderá ver o processo RMSE. Essas duas etapas caíram significativamente. O coeficiente de correlação aumenta significativamente e se aproxima de 1. Neste momento, o software não pode mais mover-se sozinho nas variáveis ​​independentes, mas Momen pode clicar manualmente nas linhas vermelhas ou azuis da imagem para alterar a entrada e saída das variáveis ​​independentes.
Após confirmação repetida, o desempenho mudará significativamente ao mover x1 ou x2 para fora, portanto, apenas x1 e x2 serão mantidos.
Em seguida, exporte os resultados.Os
resultados exportados são armazenados na área de trabalho
e insira o código.

X=[ones(13,1) x1 x2];
b=regress(y,X)%对y,x1,x2做线性回归