Série de algoritmos de planejamento de caminho: (Dijkstra)

---

---

prefácio

Esta série de artigos registra principalmente alguns pontos de conhecimento no processo de aprendizagem do algoritmo de planejamento de caminho; O principal vídeo de aprendizado vem dos "Algoritmos da série de planejamento de caminho e rastreamento de trajetória" da
Universidade de Bilibili . O link do vídeo é o seguinte: Link do vídeo Referência do artigo: link 1 , link dois小黎的Ally

---

1. Dijkstra

Introdução ao algoritmo

• O algoritmo de Dijkstra é um típico algoritmo de caminho mais curto, que é usado para calcular o caminho mais curto de um nó para outros nós.

Característica principal:

• Baseia-se no ponto inicial como o centro e se expande para a camada externa (ideia de pesquisa em largura) até atingir o ponto final.
• O algoritmo de Dijkstra usa busca em largura para resolver o problema de caminho mais curto de fonte única em grafos direcionados ou não direcionados ponderados.

ideia básica

Ao calcular o caminho mais curto em um gráfico através de Dijkstra, o ponto inicial s precisa ser especificado (ou seja, o cálculo começa no ponto de origem s).
Além disso, dois conjuntos S e U são introduzidos. O papel de S é registrar o vértice (e o comprimento do caminho mais curto correspondente) que foi calculado o caminho mais curto, e U é registrar o vértice que ainda não foi calculado o caminho mais curto (e a distância do vértice ao ponto de partida s).
Inicialmente, existe apenas o ponto inicial s em S;
existem outros vértices além de s em U, e o caminho do vértice em U é "o caminho do ponto inicial s até o vértice".
Em seguida, encontre o vértice com o caminho mais curto de U e adicione-o a S;
em seguida, atualize o vértice em U e o caminho correspondente ao vértice.
Em seguida, encontre o vértice com o caminho mais curto de U e adicione-o a S;
em seguida, atualize o vértice em U e o caminho correspondente ao vértice.
...
repita esta operação até que todos os vértices tenham sido percorridos.

Passos

(1) Inicialmente, S contém apenas o ponto inicial s; U contém outros vértices exceto s, e a distância do vértice em U é "a distância do ponto inicial s até o vértice" [por exemplo, a distância do vértice v em U é (s
, v), então s e v não são adjacentes, então a distância de v é ∞].
(2) Selecione "vértice k com a distância mais curta" de U e adicione o vértice k a S; ao mesmo tempo, remova o vértice k de U.
(3) Atualize a distância de cada vértice em U até o ponto inicial s. A razão pela qual a distância dos vértices em U é atualizada é que k foi determinado na etapa anterior como o vértice do caminho mais curto, de modo que k pode ser usado para atualizar a distância de outros vértices; por exemplo, a distância de (s, v) pode ser maior que (s, v) A distância de k)+(k,v).
(4) Repita os passos (2) e (3) até que todos os vértices sejam percorridos.
Simplesmente olhar para a teoria acima pode ser difícil de entender. Os exemplos a seguir ilustram o algoritmo.

2. Diagrama

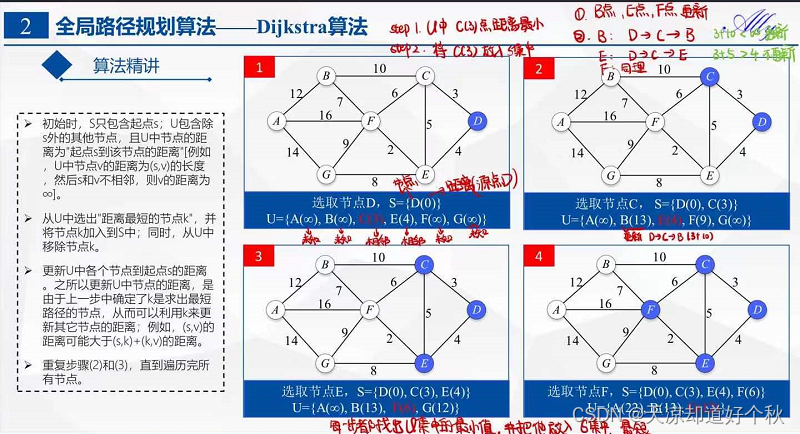
Estado inicial: S é o conjunto de vértices para os quais o caminho mais curto foi calculado e U é o conjunto de vértices para os quais o caminho mais curto não foi calculado!

Etapa 1: escolha o ponto de origem

Selecione o ponto de origem D para ingressar no conjunto S.
Neste momento, S={D(0)}, U={A(∞), B(∞), C(3), E(4), F(∞), G(∞)}. Observação: C(3) significa que a distância de C ao ponto inicial D é 3; ∞ significa distância desconhecida.

Etapa 2: encontre o ponto de menor distância, junte-se ao conjunto S e atualize o conjunto U

Selecione do conjunto U 距离最短的节点C
Adicione o nó C ao conjunto S e exclua C do conjunto U ao mesmo tempo.
Após a operação anterior, a distância do nó C em U ao ponto fonte D é a menor; portanto, adicione C a S e atualize a distância dos nós em U ao mesmo tempo. Tomando o nó F como exemplo, a distância de F a D é ∞; mas depois de somar C a S, a distância de F a D é 9=(F,C)+(C,D).
Neste momento, S={D(0), C(3)}, U={A(∞), B(23), E(4), F(9), G(∞)}.

Etapa 3: selecione o ponto de distância mínima do conjunto U, junte-se ao conjunto S e atualize o conjunto U

Adicione o nó E a S.
Após a operação anterior, a distância do nó E em U até o ponto de origem D é a menor; portanto, adicione E a S e atualize a distância dos nós em U ao mesmo tempo. Ainda tomando o nó F como exemplo, a distância de F a D era 9; mas somando E a S, a distância de F a D é 6=(F,E)+(E,D). Portanto, atualize a distância do ponto F;
neste momento, S={D(0),C(3),E(4)}, U={A(∞),B(13),F(6),G (12) }.

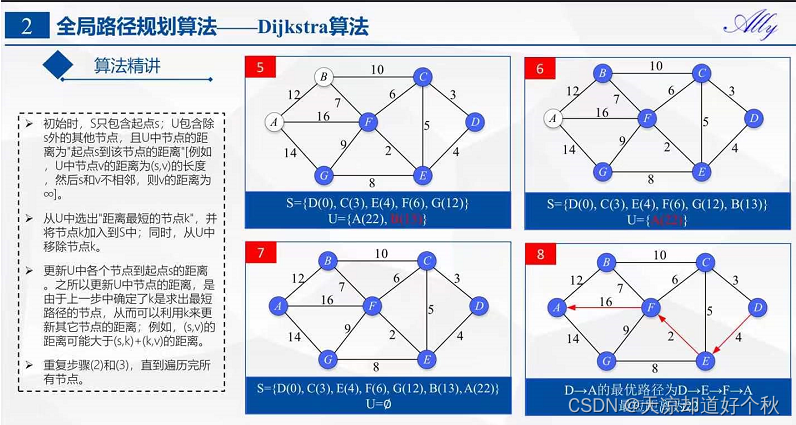
Etapa 4: selecione o ponto de distância mínima do conjunto U, junte-se ao conjunto S e atualize o conjunto U

Adicione o nó F a S.
Neste momento, S={D(0), C(3), E(4), F(6)}, U={A(22), B(13), G(12)}.

Etapa 5: selecione o ponto de distância mínima do conjunto U, junte-se ao conjunto S e atualize o conjunto U

Adicione o nó G a S.
Neste momento, S={D(0), C(3), E(4), F(6), G(12)}, U={A(22), B(13)}.

Etapa 6: selecione o ponto de distância mínima do conjunto U, junte-se ao conjunto S e atualize o conjunto U

Adicione o nó B a S.
Neste momento, S={D(0), C(3), E(4), F(6), G(12), B(13)}, U={A(22)}.

Etapa 7: selecione o ponto de distância mínima do conjunto U, junte-se ao conjunto S e atualize o conjunto U

Adicione o nó A a S.
Neste momento, S={D(0), C(3), E(4), F(6), G(12), B(13), A(22)}. U={conjunto vazio}
Neste ponto, a distância mais curta do ponto de origem D para cada nó é calculada: A(22) B(13) C(3) D(0) E(4) F(6) G( 12). Ou seja, o caminho ideal de D→A é D→E→F→A e a distância mais curta é 22

3. Implementação da programação

código mostra como abaixo:

#include<iostream>
#include<string>
using namespace std;

const int MAX = 10; //限定最大的顶点数
const int _INFINITY = 65535; //定义无穷大
class Graph
{
    
    
private:
	int vertex_num; //顶点数
	int edge_num; //边数
	int weight; //权值
	string vertex[MAX]; //顶点数组
	int edge[MAX][MAX]; //邻接矩阵
	int locate(string ch); //定位
	int *final; //标识是否已纳入最短路径，置为1表示纳入
	int *distance; //存放最短路径的权值和
	string *path;  //存放最短路径字符串

public:
	Graph(int v_n, int e_n); //构造函数
	void print_graph(); //打印邻接矩阵
	void Dijkstra(int v); //Dijkstra算法
	int Min(int *_distance, int num); //最小值
};

//定位（找到字母的下标）
int Graph::locate(string ch)
{
    
    
	int index;
	for (index = 0; index < this->vertex_num; index++)
	{
    
    
		if (this->vertex[index] == ch)
		{
    
    
			break;
		}
	}
	return index;
}

//构造函数
Graph::Graph(int v_n, int e_n) : vertex_num(v_n), edge_num(e_n)
{
    
    
	int i, j, k;
	cout << "现在请输入这" << this->vertex_num << "个顶点：" << endl;
	for (i = 0; i < this->vertex_num; i++)
	{
    
    
		cin >> this->vertex[i];
	}

	//初始化邻接矩阵
	for (i = 0; i < this->vertex_num; i++)
	{
    
    
		for (j = 0; j < this->vertex_num; j++)
		{
    
    
			if (i == j)
			{
    
    
				this->edge[i][j] = 0;
			}
			else
			{
    
    
				this->edge[i][j] = _INFINITY;
			}

		}
	}

	cout << "请依次输入边相邻的两个顶点及边的权值：" << endl;
	for (k = 0; k < this->edge_num; k++)
	{
    
    
		string first, second;
		cin >> first >> second >> this->weight;
		i = this->locate(first);
		j = this->locate(second);

		edge[i][j] = this->weight;
		//无向图
		edge[j][i] = this->weight;
	}
}

//打印
void Graph::print_graph()
{
    
    
	cout << "邻接矩阵为：" << endl;
	for (int i = 0; i < this->vertex_num; i++)
	{
    
    
		for (int j = 0; j < this->vertex_num; j++)
		{
    
    
			cout << this->edge[i][j] << "\t";
		}
		cout << endl;
	}
}

//返回最小值下标
int Graph::Min(int *_distance, int num)
{
    
    
	int index = 0, min = _INFINITY;
	for (int i = 0; i < num; i++)
	{
    
    
		if (!this->final[i] && _distance[i] < min)
		{
    
    
			min = _distance[i];
			index = i;
		}
	}
	return index;
}

//Dijkstra算法
void Graph::Dijkstra(int v)  //从源点v出发
{
    
    
	int i, j, min;
	this->path = new string[MAX];
	this->final = new int[MAX];
	this->distance = new int[MAX];
	//初始化上列数组
	for (i = 0; i < this->vertex_num; i++)
	{
    
    
		this->final[i] = 0;
		this->distance[i] = this->edge[v][i]; //初始化为源点到各t'hi点的权值大小
		if (this->distance[i] != _INFINITY)
		{
    
    
			this->path[i] = this->vertex[v] + this->vertex[i]; //当直接路径存在时，同样初始化为源点到各点的路径
		}
		else
		{
    
    
			this->path[i] = "";
		}
	}
	//初始化源点
	this->distance[v] = 0;
	this->final[v] = 1;

	//开始主循环，每次求得v到一个顶点的最短路径,所以循环次数比顶点数少一次
	for (i = 1; i < this->vertex_num; i++)
	{
    
    
		min = this->Min(distance, this->vertex_num); //求当前最小值下标
		cout << "最短路径：" << this->path[min] << "\t权值：" << this->distance[min] << endl; //输出当前最短路径
		this->final[min] = 1;
		//再次循环，修正当前最短路径及其权值和
		for (j = 0; j < this->vertex_num; j++)
		{
    
    
			//如果经过的顶点的路径比现在这条路径还短的话
			if (!this->final[j] && this->distance[j] > this->edge[min][j] + this->distance[min])
			{
    
    
				this->distance[j] = this->edge[min][j] + this->distance[min];
				this->path[j] = this->path[min] + this->vertex[j];
			}
		}
	}
	delete[]path;
	delete[]distance;
	delete[]final;
}

resultado da operação

---

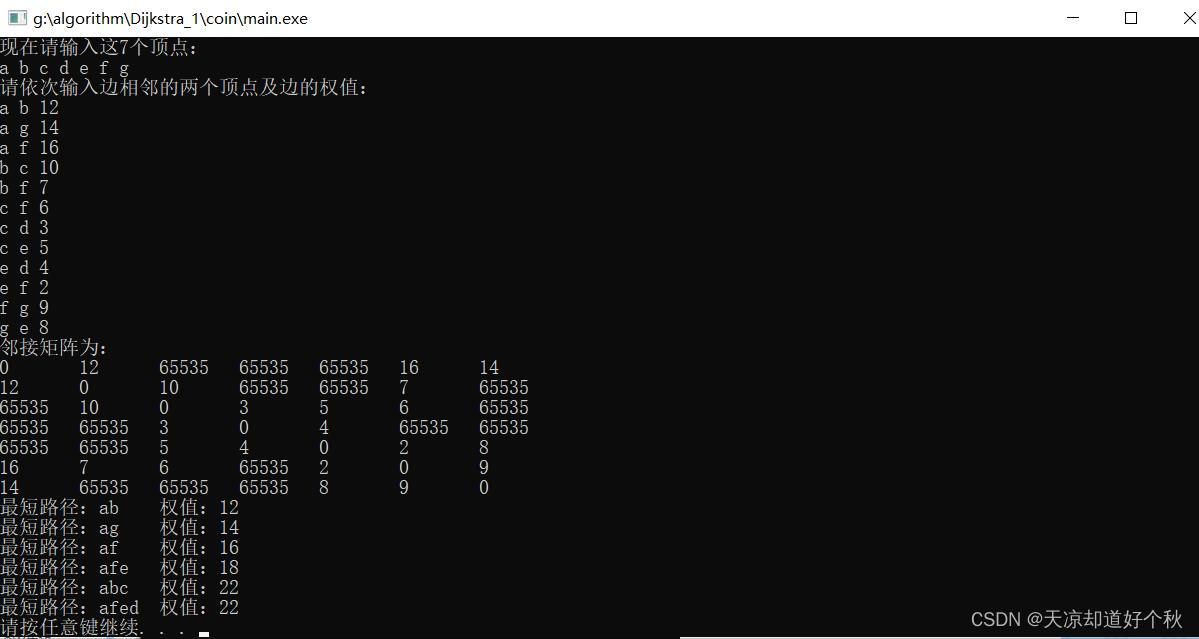
Resumir

O algoritmo de Dijkstra é, na verdade, encontrar o valor com a menor distância no conjunto U em cada etapa, colocá-lo no conjunto S e atualizar os dados no conjunto U e, após percorrer todos os nós, encontrar um valor mínimo no final ponto que é o caminho ótimo.
Por fim, o algoritmo pode obter uma árvore de caminho ideal e a complexidade é mais razoável - O(N^2).
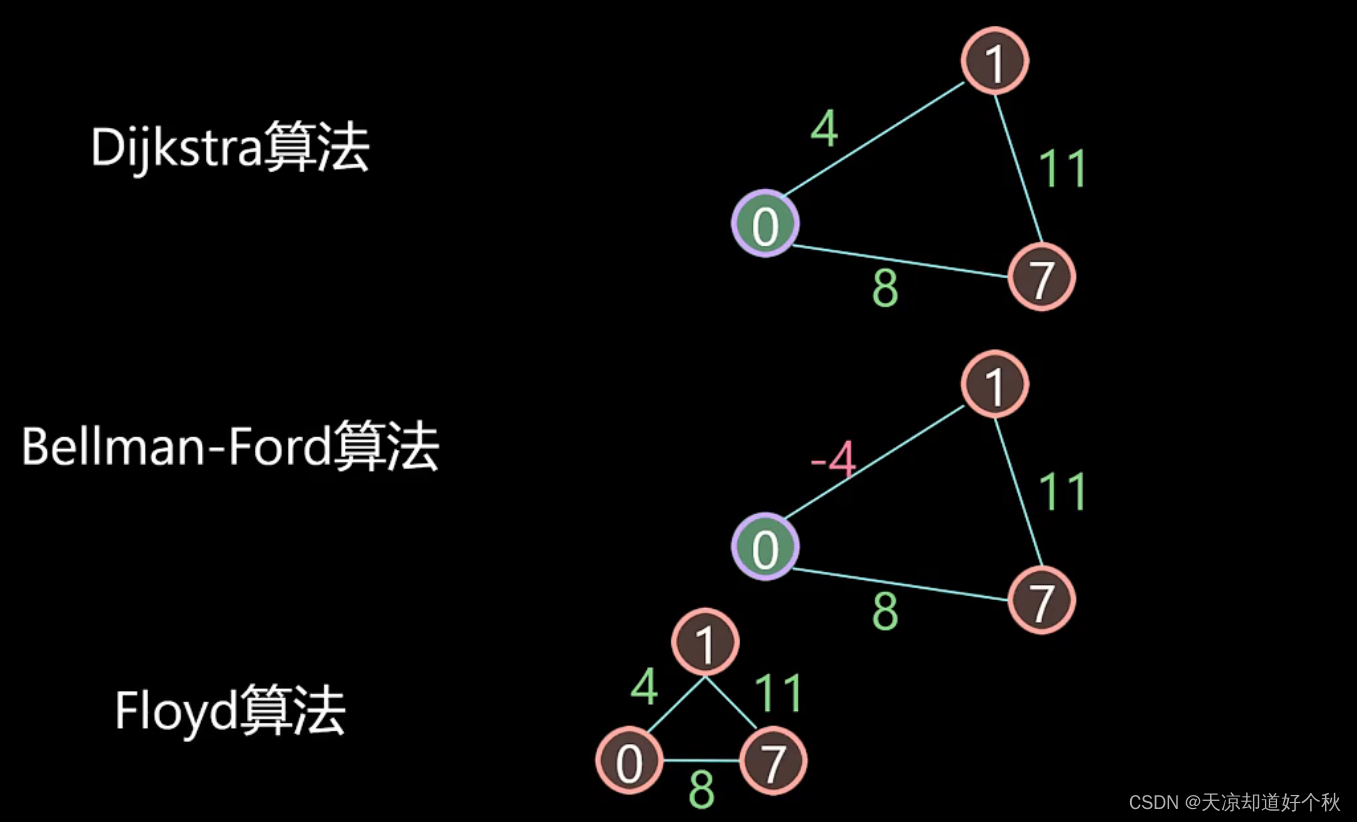
Os pesos das arestas do algoritmo de Dijkstra são todos números positivos, portanto não haverá ponderação negativa. Portanto, o ponto atual com menor distância não pode ser atualizado por outros pontos, ou seja, é garantido que cada verificação seja o ponto de menor distância .
Cada vez que um ponto com uma distância menor é selecionado, as distâncias dos outros pontos são atualizadas. Porque ir direto a um determinado ponto pode não ser tão próximo quanto um desvio.
Os pesos das arestas do algoritmo de Dijkstra são todos números positivos. Se houver números negativos, o algoritmo de Bellman-Ford é necessário. Se você quiser exigir a distância mais curta entre quaisquer dois pontos, escolha o algoritmo de Floyd.