최근에는 로봇의 동작 제어에 대한 연구로 인해 좌표계의 변환에 대한 몇 가지 정보를 검토하고 참고하여 향후 활용을 위해 기록하였다.
1. 공간점의 좌표 변환
다음 수식에서 몇 가지 식별이 지정됩니다:
1) 좌표계 A는 {A}로 표시되며 유사하게 {B}가 있습니다
. 에이프Ap 와Bp^BpBp 는각각 좌표계 {A} 및 {B}에서 점 p의 좌표를 나타냅니다.
1.1 병진 좌표 변환
A p = B p + A p BO ^Ap={^Bp}+{^Ap_{B_O}}피 _=비피 _+피 _비오.
어디에: A p BO {^Ap_{B_O}}피 _비오.{B} BO B_O 의 기원입니다비오{A}의 좌표.
1.2 회전 좌표 변환
A p = ARBB p ^Ap={^AR_B}{^Bp}피 _=아르 _비여기서
: ARB {^AR_B}아르 _비{A}에서 {B}의 회전 행렬입니다.
1.3 복합 좌표 변환
A p = ARBB p + A p BO ^Ap={^A{R_B}}{^Bp}+^Ap_{B_O}피 _=아르 _비비피 _+ㅏ피비오.
복합 변환은 실제로 위의 변환과 회전의 조합입니다.
2 회전 행렬
2.1 2차원 좌표계의 회전 행렬
2차원 좌표계에서의 회전은 비교적 단순하며 회전 각도는 θ θθ , 자유차원, 무한소:
R ( θ ) = [ cos θ − sin θ sin θ cos θ ] R(θ)=\left[\begin{matrix} cosθ & -sinθ \\ sinθ & cosθ \\end{matrix}\right]R ( i )=[cosθ _ _ _s i n θ− sin θ _ _cosθ _ _ _]
2.2 3차원 좌표계의 회전 행렬
3차원 좌표계에서의 회전은 회전축과 회전각도의 두 가지 요소를 지정해야 합니다. 따라서 서로 다른 회전 행렬이 있습니다.
2.2.1 좌표축 중심의 회전
다음 세 가지가 기본 회전 행렬입니다.
회전 행렬
RX ( θ ) = [ 1 0 0 0 cos θ − sin θ 0 sin θ cos θ ] R_X(θ)=\left[\begin{matrix} 1&0&0\ \ 0&cosθ&-sinθ\\ 0&sinθ&cosθ\\ \end{matrix}\right]아르 자형엑스( 나는 )=⎣⎡1000cosθ _ _ _s i n θ0− sin θ _ _cosθ _ _ _⎦⎤
θ θ θ θ θ
θ θ 0 0 0 0 1 0 − θ 0 cos θ ] R_Y(θ)=\left[\begin{matrix} cosθ&0&sinθ\\ 0& ;1&0\\ -sinθ& 0&cosθ\\ \end{matrix}\right]아르 자형Y( 나는 )=⎣⎡cosθ _ _ _0− 사인 θ _ _010s i n θ0cosθ _ _ _⎦⎤
비율
RZ ( θ ) = [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] R_Z(θ)=\left[\begin{matrix} cosθ&-sinθ&0\\; sinθ&cosθ&0\ \ 0&0&1\\ \end{matrix}\right]아르 자형지( 나는 )=⎣⎡cosθ _ _ _s i n θ0− sin θ _ _cosθ _ _ _0001⎦⎤
그 중에서 θ의 방향이 결정되는데, 회전축이 관찰하는 사람을 향할 때 반시계 방향 회전이 양수, 즉 오른손계, 오른손이 회전축을 잡고, 엄지손가락이 관찰자의 방향을 가리킬 때 회전축의 화살표, 다른 네 손가락의 방향은 회전 양수입니다. 그림과 같이.
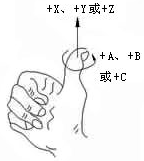
2.2.2 공간에서 임의의 축을 중심으로 한 회전 행렬
주어진 단위 벡터 K ^ = ( kx , ky , kz ) \hat K=(k_x,k_y,k_z)케이^^=( k엑스,케이y,케이지),有kx 2 + ky 2 + kz 2 = 1 k_x^2+k_y^2+k_z^2=1케이엑스2+케이와이2+케이지2=1 , 이 단위 벡터K ^ \hat K케이^ 는 회전축, 회전θ θθ 함수 정의
: RK ^ ( θ ) = [ cos θ + kx 2 ( 1 − cos θ ) kxky ( 1 − cos θ ) − kzsin θ kxkz ( 1 − cos θ ) + kysin θ kykx ( 1 − cos θ ) + kzsin θ cos θ + ky 2 ( 1 − cos θ ) kykz ( 1 − cos θ ) − kxsin θ kzkx ( 1 − cos θ ) − kxsin θ kzky ( 1 − cos θ ) + kxsin θ cos θ + kz 2 ( 1 − cos θ ) ] R_{\hat K}(θ)=\left[\begin{matrix} cosθ+k_x^2(1-cosθ)&k_xk_y(1-cosθ)-k_zsinθ&k_xk_z(1 -cosθ )+k_ysinθ\\ k_yk_x(1-cosθ)+k_zsinθ&cosθ+k_y^2(1-cosθ)&k_yk_z(1-cosθ)-k_xsinθ\\ k_zk_x(1-cosθ)-k_ysinθ&k_zk_y(1-cosθ )+k_xsinθ&cosθ+k_z^2(1-cosθ)\\ \end{matrix}\right]아르 자형케이^( 나는 )=⎣⎡cosθ _ _ _+케이엑스2( 1-cosθ ) _ _ _케이y케이엑스( 1-cosθ ) _ _ _+케이지s i n θ케이지케이엑스( 1-cosθ ) _ _ _-케이ys i n θ케이엑스케이y( 1-cosθ ) _ _ _-케이지s i n θcosθ _ _ _+케이와이2( 1-cosθ ) _ _ _케이지케이y( 1-cosθ ) _ _ _+케이엑스s i n θ케이엑스케이지( 1-cosθ ) _ _ _+케이ys i n θ케이y케이지( 1-cosθ ) _ _ _-케이엑스s i n θcosθ _ _ _+케이지2( 1-cos θ ) _ _⎦⎤
나는 내가θ 의 회전 방향 도 앞서 언급한 오른 손잡이 시스템을 따릅니다.
사실 위에서 언급한 좌표축 주위의 세 가지 기본 회전 행렬은 위 수식의 세 가지 특수한 경우입니다.
이 공식은 또한 위의 세 가지 기본 회전 행렬에서 파생될 수 있습니다. 기본 아이디어는 단위 벡터 주위의 회전을 몇 가지 알려진 작업으로 분해하는 것입니다. 1) 먼저 주어진 벡터 축을 임의의 좌표 평면(XY, YZ 또는
ZX)으로;
2) 그런 다음 주어진 벡터 축을 지금 좌표 평면의 축(X, Y 또는 Z)과 일치하도록 회전합니다.
3) 위의 세 가지 기본 회전 행렬을 사용하여 회전하고 일치시킵니다. 해당 각도θ θθ ;
4) 2)의 일을 역으로 한다
5) 1)의 일을 역으로 한다.
특정 파생 프로세스는 다른 자료에서 찾을 수 있습니다.
2.3 회전 행렬의 속성
RT = R − 1 R^T = R^{-1}아르 자형티=아르 자형− 1 , 즉 회전 행렬의 전치는 회전 행렬의 역수와 같습니다. 회전행렬은 직교행렬로, 같은 행과 열에 있는 요소의 제곱합 = 1, 다른 행과 열에 있는 요소에 해당하는 곱의 합 = 0, 행렬의 행렬식 = 1입니다. 회전 행렬의 9개 요소는 선형적으로 관련되어 있습니다.
3 여러 스핀의 조합
공간 회전은 여러 회전의 조합으로 분해될 수 있습니다.실제로는 서로 다른 회전 행렬을 여러 번 교차 곱하는 것입니다.여러 회전 행렬을 결합할 때 주의: 행렬과 행렬의 교차 곱셈 또는 행렬과 행렬의 교차 곱셈 벡터 곱셈은 결합법칙은 만족하나 일반적으로 교환법칙은 만족하지 못하므로 회전행렬의 차수에 주의해야 한다.