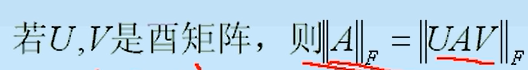[Teoria da Matriz] Norma e Função da Matriz (1)

O conceito de norma e a norma da função de matriz

Em primeiro lugar, o conteúdo deste capítulo será resumido da seguinte forma:

resolvemos o problema da função de matriz por meio do conceito de norma e usamos a função de matriz para resolver muitos problemas práticos.

---

1. Conceitos e definições

1. Norma e espaço linear normado

(1) Norma - uma função de valor real que satisfaz certas propriedades em um espaço vetorial

A propriedade 1 é chamada de definição positiva (positividade constante)
da norma . A propriedade 2 é chamada de homogeneidade da norma. Como k ∈ F, F pode ser um domínio de número complexo, então o valor de k deve ser módulo. A
propriedade 3 é chamada de norma. Desigualdade triangular

(2) Espaço linear normalizado

O espaço linear que define a norma é chamado de espaço linear normalizado

2. Exemplos de normas comuns e espaços lineares normados

(1) O comprimento no espaço interno do produto é uma espécie de norma

[Revisão] O espaço do produto interno é o espaço linear que define o produto interno: se F ∈ R, é o espaço euclidiano, se F ∈ C, é o espaço unitário.

Como o comprimento do espaço interno do produto é a norma mais comum e importante , todos nós usamos a notação || · || neste capítulo ao expressar "norma".

Observação: ao falar sobre a norma, || · || não é a apenas referência ao comprimento do vetor.

(2) Exemplos de normas em C ⁿ (transformação de p norma e norma)

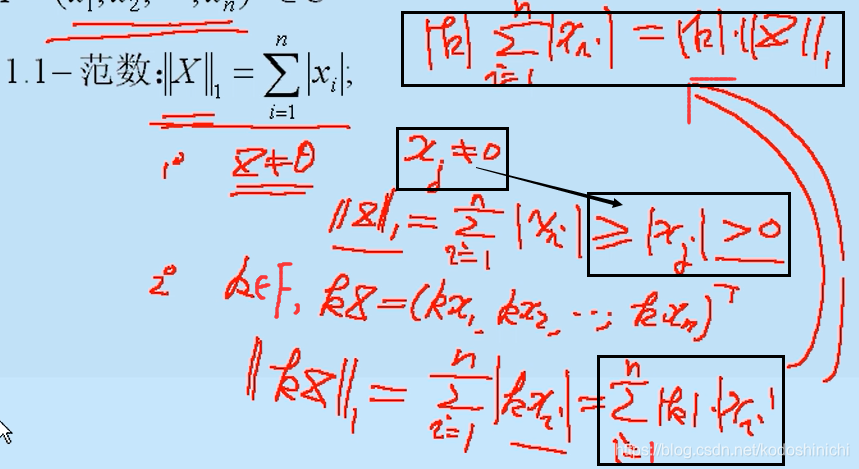
Suponha que exista algum vetor X = (x ₁ , x ₂ ,…, x _n ) ^T ∈ C ⁿ

Família norma P

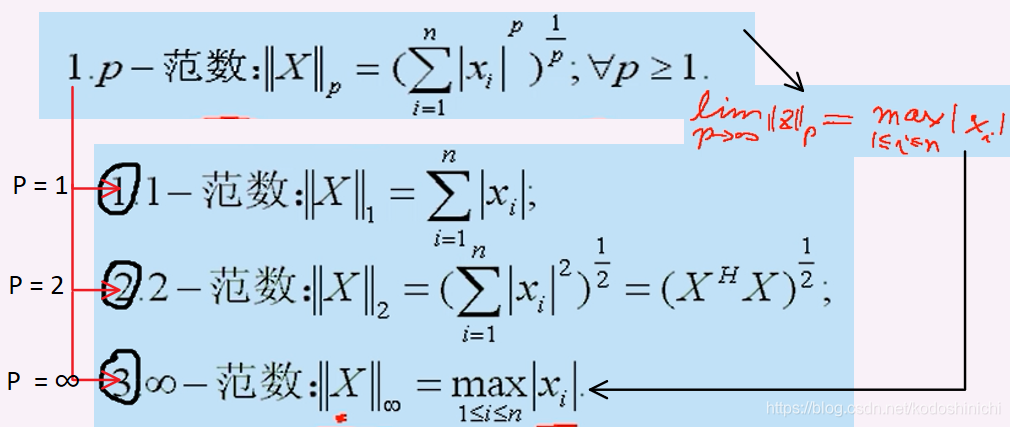
Em relação a se a norma p satisfaz as três propriedades da definição da norma, o seguinte usa a norma 1 para ilustrar:

[Nota] Propriedades de "definição positiva", "homogeneidade" e "desigualdade triangular" da norma 1-norma acima é a satisfação das propriedades correspondentes da aritmética modular .

O local marcado com uma caixa preta na figura acima é o ponto chave da prova.

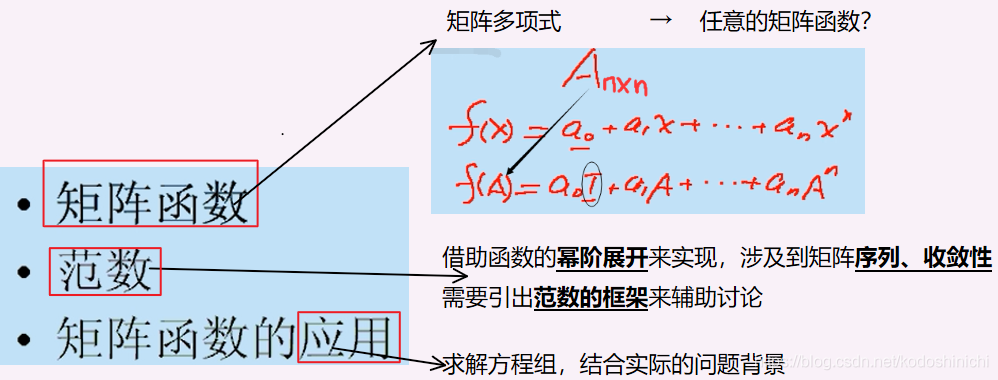
② A transformação da norma

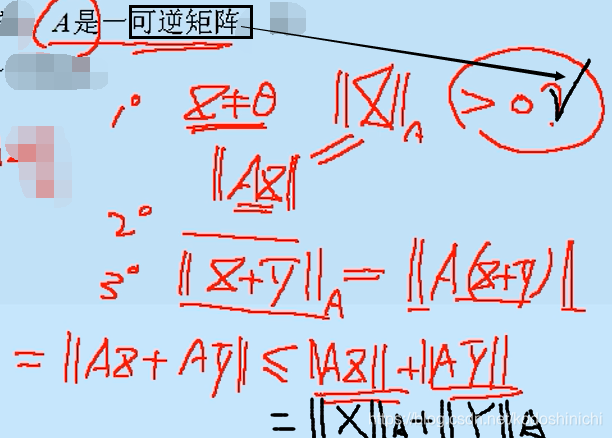
Para a definição de norma conhecida no espaço C ⁿ , outra definição de norma pode ser obtida por meio de uma matriz invertível A.

A breve prova é a seguinte:

Dica: Para uma matriz invertível A e um vetor x diferente de zero, Ax ≠ θ deve ser verdadeiro . Isso pode ser argumentado pelo método da contradição.

(3) Definição da norma em qualquer espaço linear

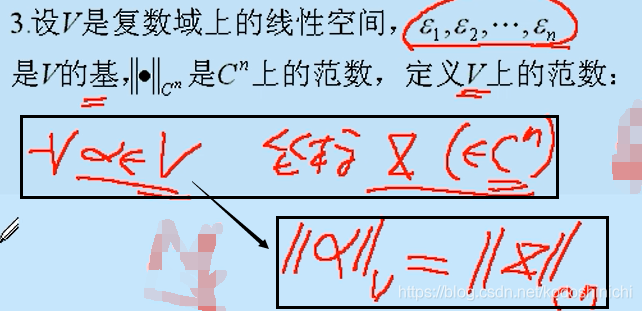
Em outras palavras, para qualquer dado espaço linear V (F∈C);
encontre um conjunto de bases neste espaço V , as coordenadas de qualquer vetor α em V no conjunto de bases são correspondentes a X ;

então, qualquer vetor arbitrário em V A norma || α || _{V do} vetor α pode ser convertida na norma do vetor da coordenada X (X∈C ⁿ ) no espaço C ⁿ || X || _{C ^ n ^} .
ps Na seção anterior, discutimos muitas definições de normas que funcionam no espaço C ⁿ , que podem ser selecionadas conforme necessário.

---

2. Norma e limite

Esta seção descreve a necessidade de definir o conceito de "norma".
A definição da norma é definir a seqüência do vetor e o limite do vetor.

1. Sequência de matriz e convergência

A convergência da seqüência da matriz ps está relacionada à definição da norma escolhida.

2. Comparabilidade de normas

Em uma palavra, se as duas normas são comparáveis , então a convergência da sequência da matriz descrita sob essas duas normas é equivalente .

Olhando para trás na definição da convergência da sequência da matriz, se duas normas diferentes forem usadas, a mesma sequência da matriz convergirá para valores diferentes?
—— Com base nisso, propomos a comparabilidade das normas.

(1) Definição

(2) Prova e compreensão O que se
segue é uma prova de que "as duas normas são comparáveis ​​↔ o valor limite da sequência da matriz sob as duas normas é o mesmo"

Dica: Uma vez que a relação de desigualdade é dada na definição de "comparável", a prova é baseada principalmente no critério de fixação do limite.

若 || η _i -η ₀ || → 0 ， 则 || η _i -η ₀ || '→ 0

De acordo com a definição comparável:
|| η _i -η ₀ || '≤ (1 / k ₁ ) || η _i -η ₀ || → 0;
|| η _i -η ₀ ||' ≥ (1 / k ₂ ) || η _i -η ₀ || → 0; de
acordo com o critério de fixação, há || η _i -η ₀ || '→ 0.

若 || η _i -η ₀ || '→ 0 ， 则 || η _i -η ₀ || → 0

A ideia é a mesma da anterior:
|| η _i -η ₀ || ≤k ₂ || η _i -η ₀ || '→ 0;
|| η _i -η ₀ || ≥k ₁ || η _i - η ₀ || '→ 0;
De acordo com o critério de fixação, existem || η _i -η ₀ || → 0

(3) Teorema

Quaisquer duas normas no espaço linear de dimensão finita V são comparáveis.

---

3. Norma da Matriz

Antes de discutirmos a definição da norma do espaço linear geral, discutimos a seguir um espaço linear mais especial - a definição da norma no espaço da matriz.

1. A definição de normas matriciais comuns

(1) Matriz p-norma

Se a matriz for dividida em linhas ou colunas , cada elemento do bloco pode aplicar a norma definida no espaço C ⁿ anterior , de modo que a definição relevante da norma da matriz possa ser derivada.

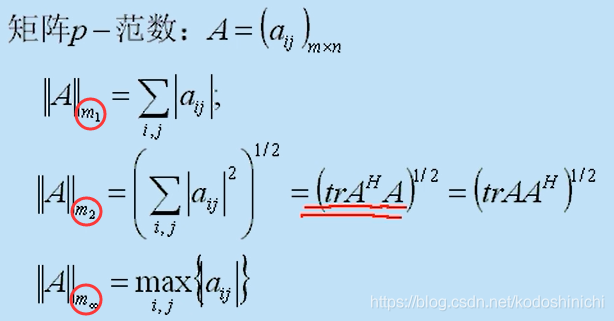
• Norma de Frobenuis (|| A || _m2 = || A || _F )

Dentre eles, atenção especial deve ser dada à
norma da matriz 2 : a norma da matriz 2 (norma de Frobenius) permanece invariante à transformação unitária.

[Prova] A conclusão acima pode ser bem provada pela definição da matriz 2-norma
|| A || _F = (trA ^H A) ^1/2 ;
|| UAV || _F = (tr (UAV) ^H (UAV) ) ^1/2 = (tr (V ^H A ^H U ^H UAV)) ^1/2
Como U é uma matriz unitária, ela satisfaz U ^H U = I
|| UAV || _F = (trV ^H A ^H AV) ^{1 / 2}
Porque V também é uma matriz unitária, de modo que V ^H = V ^-1
é satisfeito || UAV || _F = (trV ^-1 A ^HAV) ^1/2 , porque V ^-1 A ^H AV e A ^H A devem ser semelhantes, eles têm os mesmos autovalores. O traço (tr) da matriz
ps é igual à soma dos principais elementos diagonais do matriz , que também é igual à matriz A soma de todos os valores próprios de .
Portanto, a prova está completa.

(2) Norma do operador

Se você olhar para uma matriz da perspectiva da transformação linear, então a matriz A _mxn ∈ C ^mxn pode ser considerada como um vetor X que pertence ao espaço C ^m e mapeia para um vetor AX que pertence ao espaço C ⁿ .
Com base no processo de cálculo deste mapeamento linear, também queremos definir a norma correspondente.

Embora eu não vá entrar na discussão aqui, os leitores precisam cultivar uma mentalidade. Depois de definirmos a forma da norma mencionada acima, se quisermos reconhecer que ela pode de fato ser usada como uma norma, precisamos pensar sobre as seguintes questões :

• || A || A norma faz sentido?
• || A || A norma satisfaz o axioma da norma?

• Norma do operador 1, norma do operador 2 e norma do operador 3
  

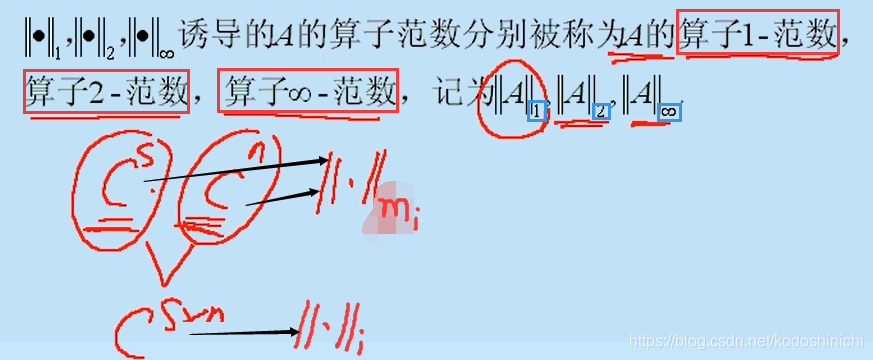
Quando o espaço original e o espaço transformado tomam || · || _mi (uma certa norma da matriz), então a norma do operador induzida por isso é || · || _i (o operador correspondente certa norma).
ps Aqui, devemos prestar atenção à forma como o subscrito é expresso, e não confundir.

2. Compatibilidade da norma da matriz

Para matrizes, tem não apenas operações de multiplicação e adição de números, mas também operações de multiplicação.
As operações de multiplicação e adição numérica baseiam-se em normas, que são padronizadas de acordo com a homogeneidade e as desigualdades trigonométricas na definição das normas;
no entanto, as operações de multiplicação correspondentes às normas ainda não foram padronizadas. Até agora apresentamos o conceito de " compatibilidade".

(1) Definição de compatibilidade

(2) Teorema 1 - norma Matriz 1, norma 2 são compatíveis e norma infinita é incompatível

Prove que a norma do infinito da matriz é incompatível, basta dar um contra-exemplo

Conforme mostrado na figura acima, considere uma matriz quadrada de 2ª ordem, sua própria norma de infinito é 1; o resultado de sua multiplicação de 2ª ordem é uma matriz quadrada de 2ª ordem, e a norma de infinito correspondente é 2.
Obviamente, a desigualdade 2≤1x1 é insatisfeito.
Portanto, incompatível.

Quanto à compatibilidade da norma da matriz 1 e da norma 2, nenhuma prova é fornecida no vídeo, os leitores podem tentar por si próprios.

A ideia de prova pode aprender com as questões de prova no link abaixo e usar a definição e a natureza da norma para dimensionar a desigualdade.
https://www.bilibili.com/read/cv4152269

(3) As normas do Teorema 2-Operadores devem ser compatíveis, o que
significa que se para três espaços lineares C ^s , C ^m e C ⁿ , três normas em seus espaços são definidas || · || _Vs , || · || _Vm e || · || _Vn ;
então esta norma e três, respectivamente, podem ser induzidas. A norma do operador é três · || || _SXM , || · || _Sxn e || · || _mxn .

"A norma do operador deve ser compatível", significando · || || _SXM , || · || _Sxn e || · || A norma _MXN três _{do Banco do México} é necessariamente atender à definição de compatibilidade.

(4) Teorema 3 - a solução da norma do operador

• A norma do operador 1 é a soma máxima do comprimento do módulo
• A norma do Operador 2 é o raio espectral da matriz A ^H A
• A norma infinita do operador é a maior soma de linhas de comprimento modular
  

Entre as três normas do operador acima, a norma espectral é a mais importante.
Até agora, há duas normas de matriz nas quais precisamos nos concentrar: uma é a norma da matriz 2 (norma de Frobenuis) e a outra é a norma do operador 2 (norma espectral).

---

[Exemplo] Resolvendo a norma-1 da matriz

De acordo com a definição da norma, ele pode ser substituído no cálculo em conformidade.
Expanda a investigação, se a norma da matriz 2 de A (é uma matriz unitária) é necessária, então, de acordo com a definição-
|| A || _m2 = (tr (A ^H A)) ^1/2 = (tr (I) ) ^1/2 = (n) ^1/2

• A norma da matriz 2 da matriz unitária de ordem n é n ^1/2
• A norma do operador 2 da matriz unitária de ordem n é 1

[Exemplo] Resolvendo a norma da matriz-2

[0]: Interprete o significado da questão, a caixa nº 0 é o nosso objetivo da prova;
[1]: A é uma matriz normal, então A deve ser transformada em diagonal por unidade Matriz de transformação, A é representado por uma matriz diagonal e uma matriz unitária correspondentemente;
[2]: De acordo com a definição da norma do operador 2, A ^H A e seu raio espectral precisam ser calculados , e pode-se saber que é semelhante a Λ ^H Λ;
[3] ： De acordo com o cálculo da matriz diagonal, a equação é obtida, e ambos os lados podem ser resolvidos ao mesmo tempo para atender aos requisitos da questão.

• A norma do operador 2 da matriz normal é o raio espectral da matriz
  [Exemplo] Resolvendo a norma da matriz 3 A
  
  prova é clara, então não vou entrar em detalhes aqui e extrair as conclusões dos exemplos.
  Para uma matriz diagonal de bloco
• A norma da sua matriz 2 é a soma dos quadrados das 2 normas de cada matriz de bloco e depois a raiz quadrada
• A norma do operador 2 é o valor máximo das 2 normas de cada operador de matriz de bloco

Habilidades de memória:
matriz 2 norma ↔ traço; operador 2 norma ↔ raio espectral ↔ toma o valor máximo
. O traço é a relação aditiva
na diagonal do bloco ; o raio espectral é o valor máximo na diagonal do bloco.