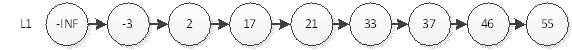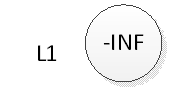Autor original: JeemyJohn
Endereço original: O princípio e a realização da tabela de pular
Leitura recomendada: Manga Algorithm: What is a Jump Table?
1. O princípio de pular mesa
Qualquer pessoa que tenha estudado a estrutura de dados sabe que a complexidade de tempo de consultar um elemento em uma lista vinculada individualmente é O (n). Mesmo se a lista vinculada individualmente for ordenada, não podemos reduzir a complexidade de tempo em 2 pontos.
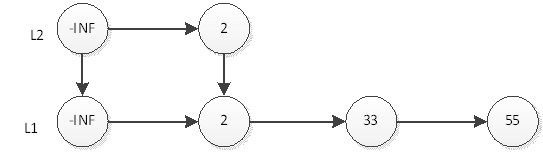
Conforme mostrado na figura acima, se quisermos consultar o nó com o elemento 55, devemos começar do nó inicial e fazer um loop até o último nó, excluindo -INF (infinito negativo), e consultar 8 vezes. Então, qual método pode ser usado para visitar 55 com menos vezes? O mais intuitivo, é claro, é um novo atalho para acessar 55.
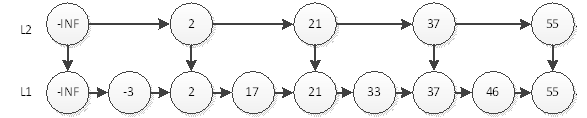
Conforme mostrado na figura acima, queremos consultar o nó com o elemento 55 e só precisamos pesquisar 4 vezes na camada L2. Nesta estrutura, consultar o elemento com um nó 46 custará 5 vezes mais consultas. Ou seja, primeiro consulte 46 em L2 e encontre o elemento 55 após 4 pesquisas. Como a lista encadeada está ordenada, 46 deve estar à esquerda de 55, portanto, não há elemento 46 na camada L2. Em seguida, voltamos ao elemento 37 e continuamos procurando por 46 na próxima camada, L1. Felizmente, só precisamos de mais uma consulta para localizar 46. Isso custou um total de 5 consultas.
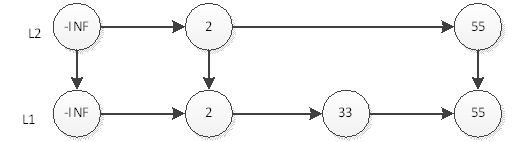
Então, como podemos pesquisar 55 mais rápido? Com a experiência acima, é fácil para nós pensar e criar um atalho.
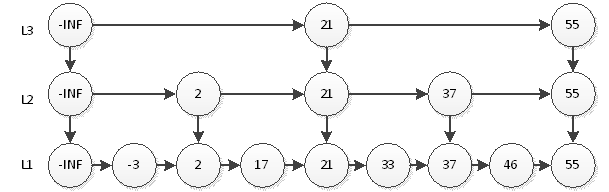
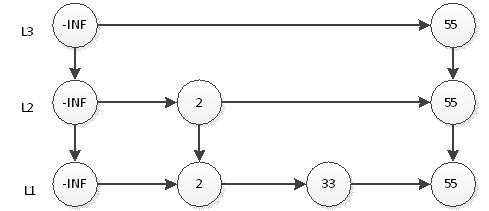
Conforme mostrado na imagem acima, precisamos apenas de 2 pesquisas para pesquisar por 55. Nessa estrutura, o elemento de consulta 46 ainda é o mais demorado, exigindo 5 consultas. Ou seja, primeiro olhe para cima 2 vezes na camada L3, depois olhe para cima 2 vezes na camada L2 e, finalmente, olhe para cima uma vez na camada L1, num total de 5 vezes. Obviamente, essa ideia é muito semelhante a 2 pontos, então nosso diagrama de estrutura final deve ser como mostrado abaixo.
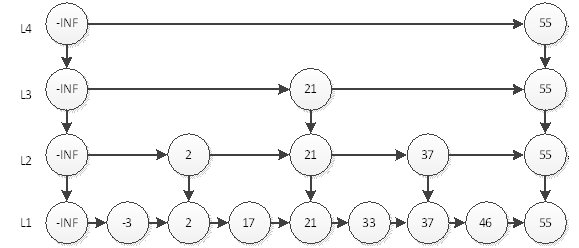
Podemos ver que a visita 46 mais demorada requer 6 consultas. Ou seja, L4 acessa 55, L3 acessa 21, 55, L2 acessa 37, 55 e L1 acessa 46. Acreditamos intuitivamente que essa estrutura tornará a consulta de um elemento de uma lista vinculada ordenada mais rápida. Então, qual é a complexidade do algoritmo?
Se houver n elementos, porque são 2 pontos, o número de camadas deve ser log n camadas (todos os logs neste artigo são baseados em 2), mais uma camada própria. Pegue a imagem acima como exemplo, se ela tiver 4 elementos, então as camadas são L3 e L4, mais sua própria L2, um total de 3 camadas; se ela tiver 8 elementos, então é 3 + 1 camadas. A consulta mais demorada é, naturalmente, para acessar todas as camadas, e leva logn + logn, que é 2logn. Por que é 2 vezes o logn? Vamos pegar 46 na figura acima como exemplo. A consulta ao 46 precisa acessar todas as camadas e cada camada deve visitar 2 elementos, o elemento do meio e o último elemento. Portanto, a complexidade do tempo é O (logn).
Até agora, apresentamos a lista de atalhos ideal, mas e se você quiser inserir ou excluir um elemento da imagem acima? Por exemplo, se quisermos inserir um elemento 22, 23, 24 ..., naturalmente na camada L1, inserimos esses elementos após o elemento 21, e as camadas L2 e L3? Temos que considerar como ajustar a conexão após a inserção, a fim de manter esta estrutura de lista de omissões ideal. Sabemos que o ajuste de uma árvore binária equilibrada é uma dor de cabeça, canhoto, destro, canhoto, canhoto, canhoto, canhoto, canhoto, canhoto, canhoto, canhotos e canhotos. Felizmente, não precisamos ajustar a conexão por meio de operações complicadas para manter uma tabela de salto perfeita. Existe um algoritmo de inserção baseado em estatísticas de probabilidade que também pode obter eficiência de consulta com uma complexidade de tempo de O (logn). Este tipo de tabela de salto é o que realmente queremos alcançar.
2. Análise das etapas de realização da tabela de salto
Vamos discutir a inserção primeiro. Vejamos a estrutura da tabela de salto ideal. O número de elementos na camada L2 é 1/2 do número de elementos na camada L1 e o número de elementos na camada L3 é 1/2 de o número de elementos na camada L2. analogia. A partir daqui, podemos pensar que, contanto que tentemos garantir que o número de elementos na camada superior seja metade dos elementos na próxima camada ao inserir, nossa lista de atalhos pode se tornar uma lista de atalhos ideal. Então, como podemos garantir que o número de elementos na camada anterior seja 1/2 do número de elementos na próxima camada ao inserir? É fácil, basta lançar uma moeda! Assumindo que o elemento X deve ser inserido na lista de ignorar, é óbvio que X deve ser inserido na camada L1. Portanto, devo inserir X na camada L2? Esperamos que o número de elementos na camada superior seja 1/2 do número de elementos na camada inferior, então temos uma probabilidade de 1/2 de que queremos que X seja inserido na camada L2, então jogue uma moeda , insira-o na frente e não insira-o na parte traseira. Então, L3 deve inserir X? Em comparação com a camada L2, ainda esperamos que a probabilidade de 1/2 seja inserida, então continue jogando a moeda! Por analogia, a probabilidade de que o elemento X seja inserido na enésima camada é de (1/2) n vezes. Desta forma, podemos inserir um elemento na lista de atalhos.
Aqui está a figura acima como exemplo: o estado de teste inicial da tabela de salto é o seguinte, não há nenhum elemento na tabela:
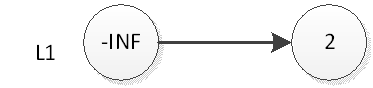
Se quisermos inserir o elemento 2, primeiro insira o elemento 2 na parte inferior, conforme mostrado abaixo:
Então jogamos uma moeda, o resultado é cara, então precisamos inserir 2 na camada L2, conforme mostrado abaixo:
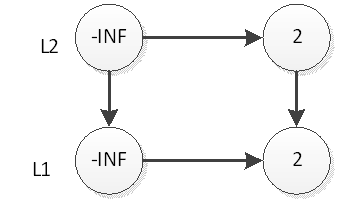
Continue a jogar a moeda, o resultado é o oposto, então a operação de inserção do elemento 2 é interrompida e a estrutura da mesa após a inserção é como mostrado na figura acima. Em seguida, inserimos o elemento 33, que é o mesmo que o elemento 2, agora inserimos 33 na camada L1, conforme mostrado abaixo:
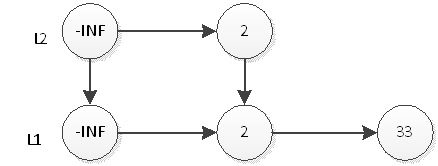
Em seguida, lance uma moeda, o resultado é o oposto, então a operação de inserção do elemento 33 está encerrada e a estrutura da mesa após a inserção é como mostrado na figura acima. Em seguida, inserimos o elemento 55, primeiro insira 55 em L1, após a inserção, conforme mostrado abaixo:
Em seguida, lance uma moeda, o resultado é cara, então 55 precisa ser inserido na camada L2, conforme mostrado abaixo:
Continue a jogar a moeda, e o resultado é cara novamente, então 55 precisa ser inserido na camada L3, conforme mostrado abaixo:
Por analogia, inserimos os elementos restantes. Obviamente, devido à pequena escala, o resultado pode não ser uma lista de atalhos ideal. Mas se a escala do número de elementos n for grande, os alunos que estudaram a teoria da probabilidade sabem que a estrutura da mesa final deve estar muito próxima da mesa de salto ideal.
Claro, esse tipo de análise é perceptualmente muito direto, mas a prova da complexidade do tempo é realmente complicada. Não vou entrar nisso aqui. Se você estiver interessado, pode ler o artigo na tabela de salto. Vamos discutir a exclusão novamente. Não há nada a dizer sobre a exclusão. Basta excluir o elemento diretamente e, em seguida, ajustar o ponteiro após excluir o elemento. É exatamente igual à operação normal de exclusão da lista vinculada. Vamos discutir a complexidade de tempo novamente. A complexidade de tempo de inserir e excluir é a complexidade de tempo de consultar a posição de inserção do elemento. Não é difícil de entender, por isso é O (logn).
3. Implementação do código
No Capítulo 2, usamos o sorteio para determinar o nível mais alto de inserção de novo elemento, o que obviamente não pode ser implementado no programa. No código, usamos a geração de números aleatórios para obter o nível mais alto de inserção de novos elementos. Vamos primeiro estimar a escala de n e, em seguida, definir o número máximo de níveis maxLevel da tabela de salto. Em seguida, a camada inferior, que é a 0ª camada, deve inserir elementos com uma probabilidade de 1; a camada mais alta, que é a camada maxLevel, tem a probabilidade de inserção do elemento. É 1/2 ^ maxLevel.
Primeiro, geramos aleatoriamente um inteiro r variando de 0 a 2 ^ maxLevel-1. Então, a probabilidade de que o elemento r seja menor que 2 ^ (maxLevel-1) é 1/2, a probabilidade de que r seja menor que 2 ^ (maxLevel-2) é 1/4, ..., a probabilidade de que r seja menor que 2 é 1/2 ^ (maxLevel- 1) A probabilidade de r ser menor que 1 é 1/2 ^ maxLevel.
Por exemplo, suponha que maxLevel seja 4, então o intervalo de r é 0-15, a probabilidade de r ser menor que 8 é 1/2, a probabilidade de r ser menor que 4 é 1/4, a probabilidade de r ser menor que 2 é 1/8 e r é menor que 1. A probabilidade de é 1/16. 1/16 é exatamente a probabilidade de inserir elementos na camada maxLevel, 1/8 é exatamente a probabilidade de inserir elementos no maxLevel camada e assim por diante.
Através desta análise, podemos primeiro comparar r e 1, se r <1, então o elemento deve ser inserido abaixo da camada maxLevel; caso contrário, compare r e 2, se r <2, então o elemento deve ser inserido no maxLevel- 1 camada abaixo; compare r e 4, se r <4, então o elemento será inserido abaixo da camada maxLevel-2 ... Se r> 2 ^ (maxLevel-1), então o elemento será inserido apenas na parte inferior camada.
A análise acima é a chave para o algoritmo de número aleatório. O algoritmo não tem nada a ver com a implementação e a linguagem, mas é mais fácil para os programadores Java entenderem a lista de salto da implementação do código Java. Abaixo, postarei a implementação do código Java de outra pessoa.
/*************************** SkipList.java *********************/
import java.util.Random;
public class SkipList<T extends Comparable<? super T>> {
private int maxLevel;
private SkipListNode<T>[] root;
private int[] powers;
private Random rd = new Random();
SkipList() {
this(4);
}
SkipList(int i) {
maxLevel = i;
root = new SkipListNode[maxLevel];
powers = new int[maxLevel];
for (int j = 0; j < maxLevel; j++)
root[j] = null;
choosePowers();
}
public boolean isEmpty() {
return root[0] == null;
}
public void choosePowers() {
powers[maxLevel-1] = (2 << (maxLevel-1)) - 1; // 2^maxLevel - 1
for (int i = maxLevel - 2, j = 0; i >= 0; i--, j++)
powers[i] = powers[i+1] - (2 << j); // 2^(j+1)
}
public int chooseLevel() {
int i, r = Math.abs(rd.nextInt()) % powers[maxLevel-1] + 1;
for (i = 1; i < maxLevel; i++)
if (r < powers[i])
return i-1; // return a level < the highest level;
return i-1; // return the highest level;
}
// make sure (with isEmpty()) that search() is called for a nonempty list;
public T search(T key) {
int lvl;
SkipListNode<T> prev, curr; // find the highest nonnull
for (lvl = maxLevel-1; lvl >= 0 && root[lvl] == null; lvl--); // level;
prev = curr = root[lvl];
while (true) {
if (key.equals(curr.key)) // success if equal;
return curr.key;
else if (key.compareTo(curr.key) < 0) { // if smaller, go down,
if (lvl == 0) // if possible
return null;
else if (curr == root[lvl]) // by one level
curr = root[--lvl]; // starting from the
else curr = prev.next[--lvl]; // predecessor which
} // can be the root;
else { // if greater,
prev = curr; // go to the next
if (curr.next[lvl] != null) // non-null node
curr = curr.next[lvl]; // on the same level
else { // or to a list on a lower level;
for (lvl--; lvl >= 0 && curr.next[lvl] == null; lvl--);
if (lvl >= 0)
curr = curr.next[lvl];
else return null;
}
}
}
}
public void insert(T key) {
SkipListNode<T>[] curr = new SkipListNode[maxLevel];
SkipListNode<T>[] prev = new SkipListNode[maxLevel];
SkipListNode<T> newNode;
int lvl, i;
curr[maxLevel-1] = root[maxLevel-1];
prev[maxLevel-1] = null;
for (lvl = maxLevel - 1; lvl >= 0; lvl--) {
while (curr[lvl] != null && curr[lvl].key.compareTo(key) < 0) {
prev[lvl] = curr[lvl]; // go to the next
curr[lvl] = curr[lvl].next[lvl]; // if smaller;
}
if (curr[lvl] != null && key.equals(curr[lvl].key)) // don't
return; // include duplicates;
if (lvl > 0) // go one level down
if (prev[lvl] == null) { // if not the lowest
curr[lvl-1] = root[lvl-1]; // level, using a link
prev[lvl-1] = null; // either from the root
}
else { // or from the predecessor;
curr[lvl-1] = prev[lvl].next[lvl-1];
prev[lvl-1] = prev[lvl];
}
}
lvl = chooseLevel(); // generate randomly level
newNode = new SkipListNode<T>(key,lvl+1); // for newNode;
for (i = 0; i <= lvl; i++) { // initialize next fields of
newNode.next[i] = curr[i]; // newNode and reset to newNode
if (prev[i] == null) // either fields of the root
root[i] = newNode; // or next fields of newNode's
else prev[i].next[i] = newNode; // predecessors;
}
}
}
原文地址:https://blog.csdn.net/u013709270/article/details/53470428