記事のディレクトリ
- 章1
- 1.1はじめに
- 1.2システムおよび制御基本事項
- システムの1.2.1コンセプト
- 1.2.2入出力モデリングプロセス
- 国家の1.2.3ザ・コンセプト
- 1.2.4ザ・状態空間モデリングプロセス
- 動的システムの1.2.5サンプルパス
- 1.2.6状態空間
- 決定論と確率システム
- コントロールの1.2.7コンセプト
- フィードバックの1.2.8ザ・コンセプト
- 1.2.9離散時間システム
- 1.3離散事象システム
- イベントの1.3.1コンセプト
- 離散事象システムの1.3.2特性プロパティ
- 離散事象システムの研究における抽象化の1.3.3ザスリーレベル
- 離散事象システムの1.3.4例
- 1.3.5ハイブリッドシステム
- SYSTEM分類の1.4概要
- 1.5システム理論の目的
概要 第一章では、離散事象システムの定義特性を記述する
章1
1.1はじめに
まず、第一の目的は、「システム」を記述するだけで、それが何を意味するのかで、かつ合理的であるシステム理論に関連する基本的な概念を紹介します。
2つ目の目的は、離散事象システムの我々の研究の励起特性を明らかにするための有用な分類システムを研究することです。
1.2システムおよび制御基本事項
このセクションでは、我々は意志慎重にではなく、システム理論の基本的な概念に非公式の紹介。我々は前進するように、我々は区別して分類システムのための基本的な基準を決定します。
システムの1.2.1コンセプト
システムの3つの文書の定義:

これらは、定義2つの顕著な特徴を。まず、システムの「成分」対話組成こと、第二に、システムの「機能」が実行に関連付けることができます。また、注目すべきは、システムがあることであるべきではありません常に関連付けられている物理オブジェクトと自然の法則。例えば、システム理論は、経済制度や人間の行動やモデリング個体群動態を記述するための非常に便利なフレームワークを提供します。
1.2.2入出力モデリングプロセス
1.ビルドプロセスの入力と出力モデル:
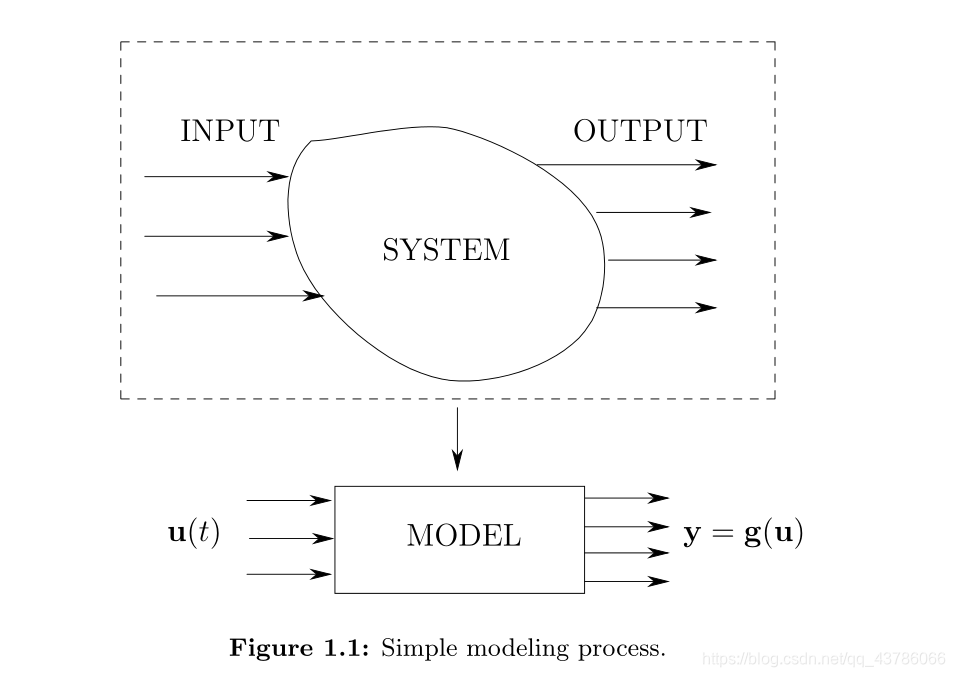
2の数学的説明:

例:
を1aA分圧器システム-
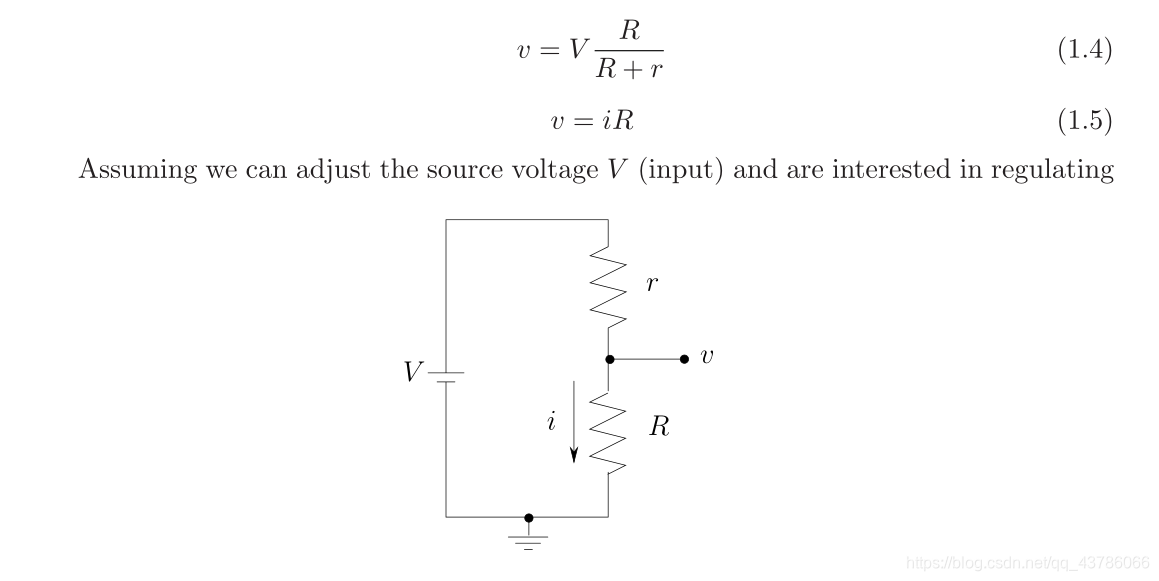
システム上でモデル化することができる
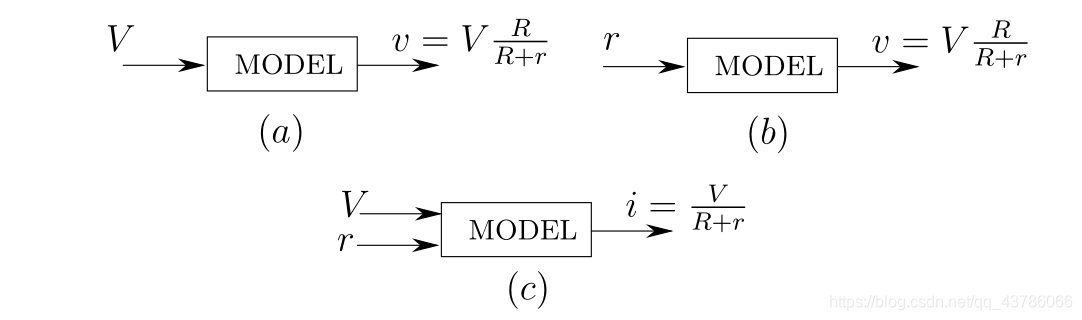
注:について同じ基本的なシステムさせることができる異なるモデルを想定します。もちろん、変数間の関数関係は変化しませんし、入力と出力を変更します。
前記分類システム
の静的および動的システム;.
動的システム、典型的には、入力の過去の出力値に依存するシステムです。したがって、「メモリ」と力学系の入力履歴を必要としないシステムの静的な出力を決定するためには当てはまりません。私たちは、実際には動的なシステムをより興味深いものになる、動的システム上でほぼ独占的に焦点を当てます。
。Bの時不変と時間的に変化する動的システム

要するに、参照:入力をu(t)は出力y(t)を生じさせる場合には、任意のτのために、入力u(T-τ)は出力y(T-τをもたらします)、それは時不変系です。
国家の1.2.3ザ・コンセプト

注:状態ベクトル表現
1.2.4ザ・状態空間モデリングプロセス
1.状态方程

2.状态空间
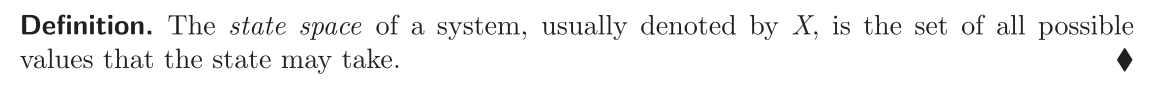
3.大多数系统和控制理论都基于以下形式的微分方程

注:加粗的字母代表向量
也可用这种表示方法:

4.黑箱方法

**注:**我们的任务是通过尝试不同种类的输入并每次观察结果输出来推断出关于“黑匣子”的所有信息。相反,状态空间建模过程包含一些由状态方程(1.10)捕获的附加信息。如图1.6所示。请注意,在此框架中,我们首先可以专注于推导状态方程,从而推导系统的动力学。然后,我们可以根据感兴趣的问题选择输出变量,并观察它们在不同输入函数中的作用。
5.线性和非线性系统

注:1.线性时不变系统的研究沿着两条平行的路径进行:时域,其中一个使用微分方程模型(1.25)和(1.26),而频域,其中一个使用由以下方程得出的代数方程(1.25)和(1.26)的拉普拉斯变换。两种方法都有各自的优点和缺点。

可以说,模型(1.25)和(1.26)构成了现代系统理论的基石。
2.所有动态系统都可以通过微分方程建模,无论它们是多么的非线性和复杂。尽管这些模型在系统和控制理论中确实是非常有用的,但我们很快就会看到,对于我们需要考虑的离散事件系统,微分方程根本无法捕获基本的动态行为,否则它们会导致设计和控制解决方案对于许多实际目的而言不够准确。
1.2.5 Sample Paths of Dynamic Systems
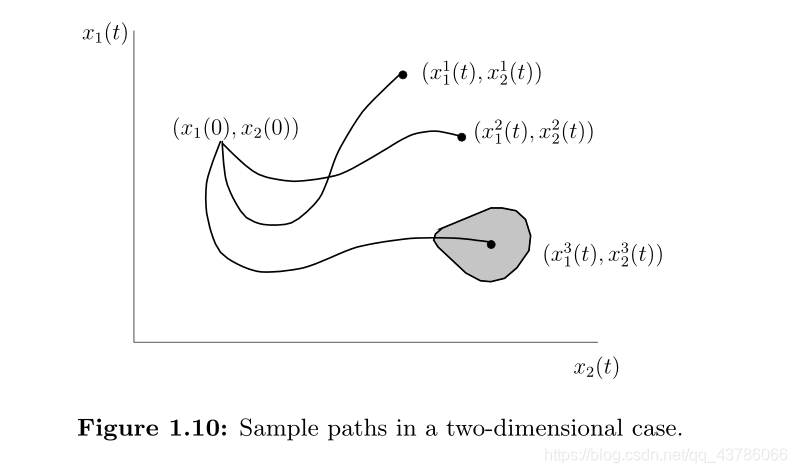
n维状态向量x(t)可以取的所有可能值都定义了n维空间。假设我们将t固定在给定的样本路径上;这指定了该空间中的一个点(向量)。随着t的变化,将访问不同的点,从而定义一条曲线,我们也可以将其视为系统的状态轨迹。在图1.10所示的二维情况下,这是最好的可视化。初始条件(x1(0),x2(0))对应于该空间中的一个点。对于输入函数u(t)= u1(t),状态用(x1 1(t),x1 2(t))表示。随着t的变化,(x1 1(t),x1 2(t))代表一个新点,从而产生了描述状态如何在此空间中移动的轨迹。在图1.10中,针对不同的输入u1(t),u2(t),…显示了不同的采样路径。在数学上,该表示对应于从函数x1(t),x2(t)中消除变量t以获得一些函数h(x1,x2)=0。此函数在二维空间中的图形表示定义了示例路径。
1.2.6 State Spaces
Continuous-State and Discrete-State Systems
对系统进行分类的另一种方法是基于为模型选择的状态空间的性质。在连续状态模型中,状态空间X是由实数(或有时为复数)的所有n维向量组成的连续体。通常,X是有限维的(即n是有限数),尽管在某些情况下X是无限维的。这通常会导致(1.10)中的微分方程式和相关的分析技术。在离散状态模型中,状态空间是离散集。在这种情况下,典型的采样路径是分段常数函数,因为状态变量仅允许在离散的时间点从一个离散的状态值跳到另一个离散的状态点(请参见下面的示例1.8)。自然地,在许多情况下混合模型可能适用,即某些状态变量是离散的而某些状态是连续的。
离散状态系统的动态行为通常更易于可视化。这是因为状态转换机制通常基于简单的逻辑语句,其形式为“如果发生某些特定事件并且当前状态为x,则下一个状态变为x’。”但是,正式表达状态方程并求解它们的数学机制可能要复杂得多,因为我们将有机会发现这一点。另一方面,连续状态模型最终可以简化为微分方程的分析,为此可以使用许多数学工具和通用求解技术。
Example:
仓库系统:
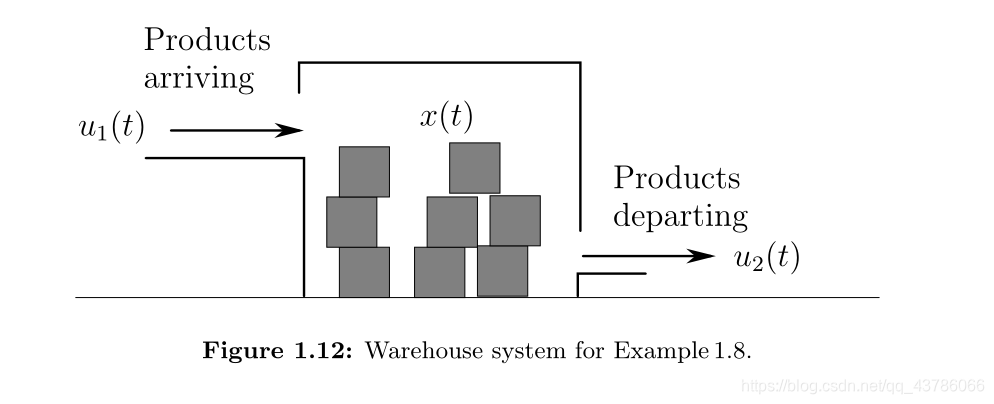

于是可得样本路径:
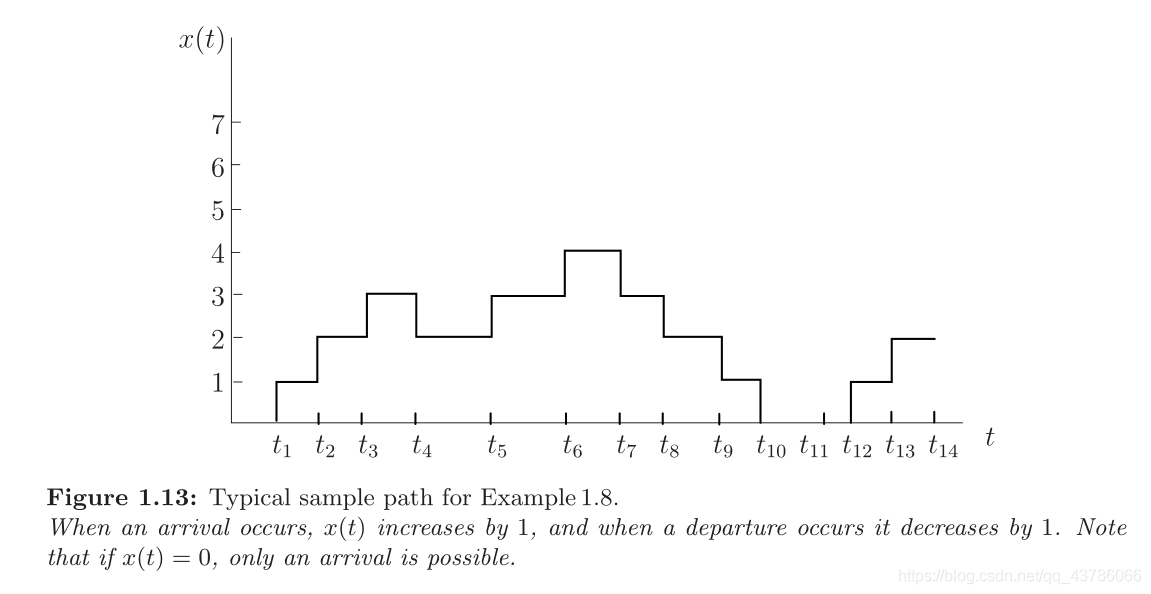

Deterministic and Stochastic Systems
如果系统的输出变量中至少有一个是随机变量,则我们将其定义为随机的。否则,该系统被认为是确定性的。一般而言,随机动态系统的状态定义了一个随机过程,其行为只能用概率来描述。因此,在确定性系统中,对于所有t≥t0都给出输入u(t),可以评估状态x(t)。在随机系统中,时间t处的状态是一个随机向量,只有其概率分布函数可以评估。
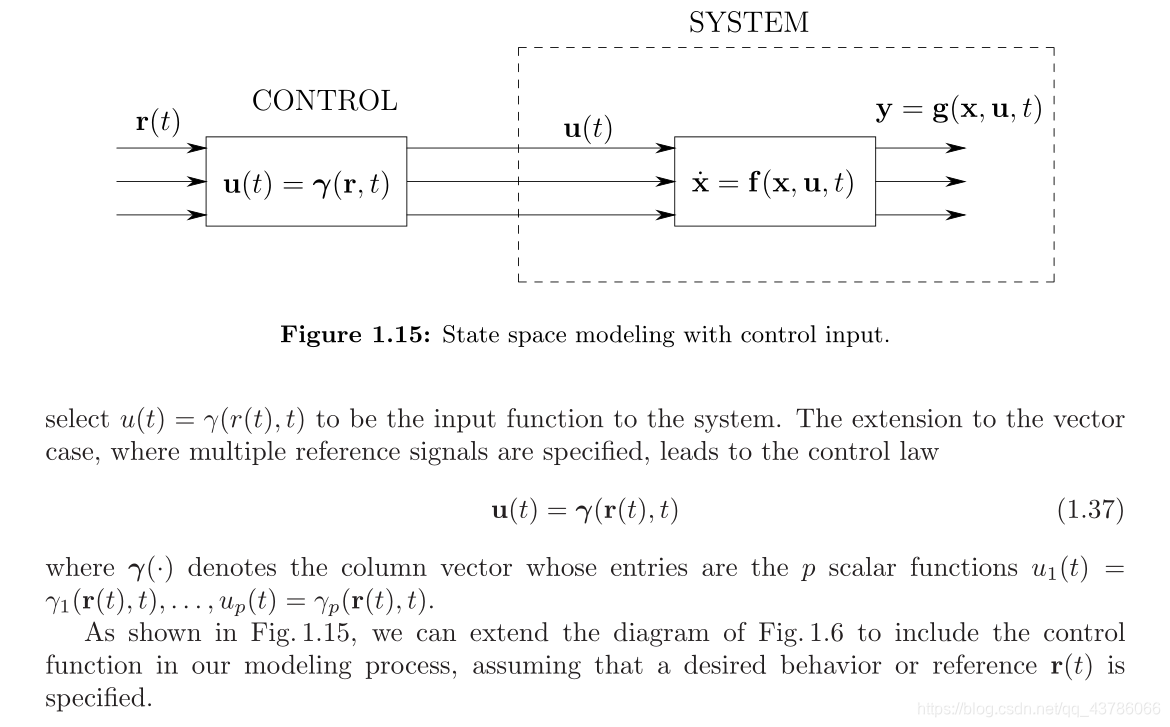
1.2.7 The Concept of Control
控制定律

给定函数r(t)为当前系统描述“期望的行为”,我们作为控制器的任务是:
Example:

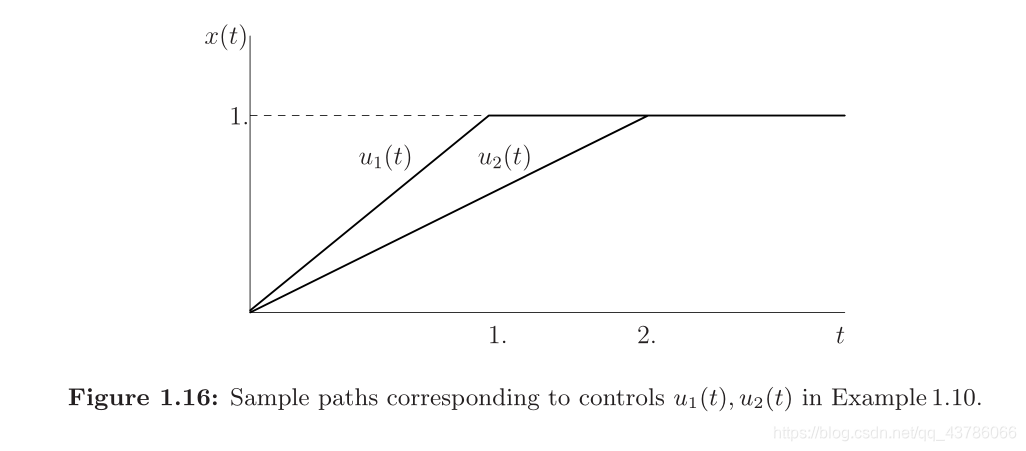
1.2.8 The Concept of Feedback

Open-Loop and Closed-Loop Systems
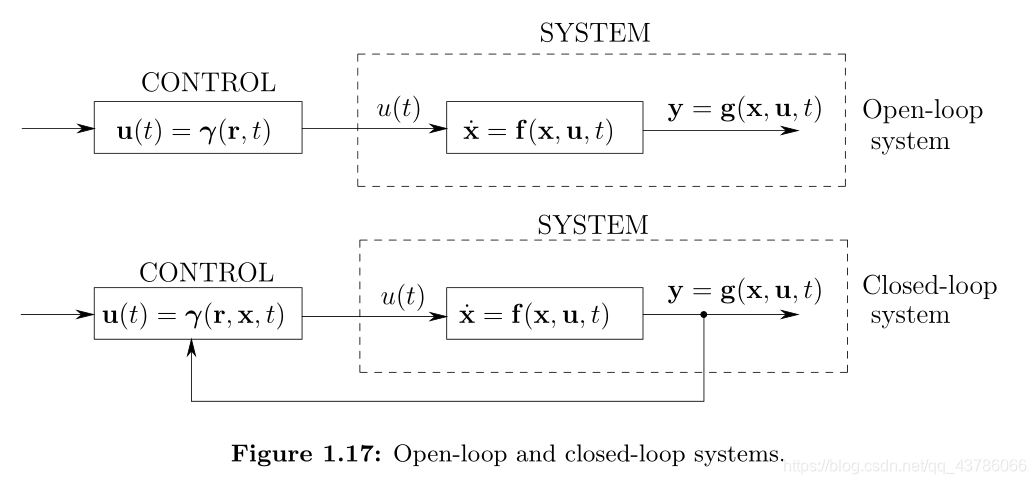
这两种控制形式之间的区别是根本的。在开环控制中,无论输入如何影响观察到的输出,输入都会保持固定。在闭环控制中,输入取决于它对输出造成的影响。图1.17说明了这种区别,它代表了我们将要关注的建模过程的最完整形式。在闭环情况下,假定反馈的信息是状态变量(在图中未明确显示)的某些函数,然后将其包含在控制定律γ(·)中。请注意,在模型中包含有关所有状态变量的信息可能不是理想的(或实际上是可行的)。图中通过反馈过程形成的“回路”引起了术语“闭环”系统。
1.2.9 Discrete-Time Systems
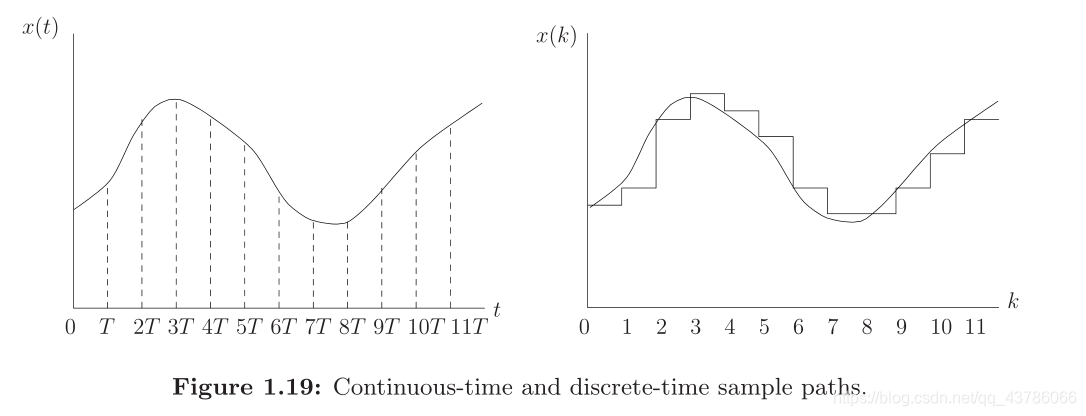
实际上,到目前为止开发的所有框架都可以用输入和输出函数u(t)和d y(t)替换为序列u(k)和d y(k)来复制。类似地,状态x(t)被x(k)代替。

1.3 DISCRETE EVENT SYSTEMS
当系统的状态空间自然地由离散集(如{0,1,2,…})描述,并且状态转换仅在离散时间点观察到时,我们将这些状态关联起来,过渡成“事件”并谈论“离散事件系统”。我们首先研究这些系统的基本特征,然后研究一些离散事件系统的熟悉示例,从而开始对这些系统的研究。
1.3.1 The Concept of Event
事件应被认为是瞬间发生并引起从一种状态值到另一种状态值的转变。
为了我们的目的,我们将使用符号e表示事件。当考虑受不同类型的事件影响的系统时,我们假设可以定义一个事件集E,其元素就是所有这些事件。显然,E是一个离散集。
Example:随机漫步
“随机行走”是一些有趣过程的有用模型,包括一些机会游戏。当二维随机游走时,我们可以将其可视化为一个粒子,该粒子可以在四个方向之一(北,南,西或东)上一次移动一个距离(“步长”)。假定方向是随机选择的,并且与当前位置无关。该系统的状态是在平面上测量的粒子(x1,x2)的位置,其中x1,x2仅采用整数值,也就是说,状态空间是离散集X = {(i,j): i,j = …,− 1,0,1,…}。在这种情况下,自然事件集是E = {N, S, W, E},对应于“北上一步”,“南上一步”,“西上一步”和“东上一步”这四个事件。图1.20显示了(x1,x2)空间中的样本路径(如图1.10所示),该路径由初始状态(0,0)和事件序列{E,S,W,W,N,N,W }确定。
Time-Driven and Event-Driven Systems
“时钟”是驱动典型采样路径的因素。由于连续的状态变量,状态每次发生变化都会使状态发生变化,随着时间不断变化。由于这种特性,我们将这类系统称为时间驱动系统。在这种情况下,时间变量(连续时间为t或离散时间为k)是自然自变量,显示为所有输入,状态和输出函数的参数。

1和2之间的区别分别引起了时间驱动系统和事件驱动系统这两个术语。正如我们已经看到的,连续状态系统本质上是受时间驱动的。但是,在离散状态系统中,这取决于状态转换是否时钟同步或异步发生,如上面的方案2所示。显然,事件驱动系统的建模和分析更加复杂,因为有几种异步事件定时机制需要指定,这是我们对系统的理解的一部分。
值得指出的是,事件驱动状态转换的概念与**计算机系统中“中断”**的概念相对应。虽然计算机中的许多功能是通过时钟同步的,因此是受时间驱动的,但操作系统的设计还可以响应随时可能发生的异步调用。例如,由于特定事件,可能会发生外部用户请求或超时消息,但完全独立于计算机时钟。
上面的随机漫步修改下规则:
假设有四个不同的角色,每个角色负责沿单个方向(N,S,W或E)移动粒子。每个玩家的行为都是通过偶尔发出一个使粒子向其方向移动的信号进行的。这导致了由这四个异步运行的播放器定义的事件驱动系统。例如,假设玩家N在离散时刻{7,9}发出信号,S在{2,10}发出信号,W在{4,6}发出信号,E在{1,11}发出信号。图1.21以时序图的形式显示了结果采样路径,其中状态转换是事件驱动的。假定初始状态为(0,0)。
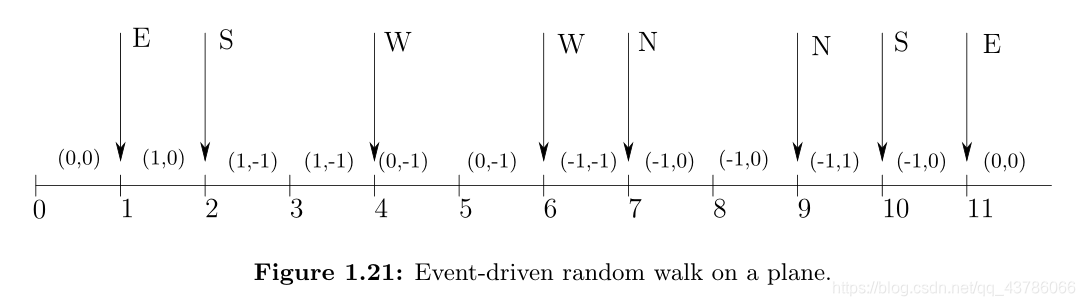
在例1.14中,假定两个事件永远不会在同一时刻发生。如果是这种情况,那么最终的状态转换应反映两个事件的发生。例如,假设在时刻1,E和S均发出信号。我们可以轻易地假设两个事件中的任何一个发生在另一个事件之前(但同时),因为两种情况下的结果状态最终都是(1,-1)。当然,并非总是如此。通常,两个事件影响状态的确切顺序可以改变世界。例如,假设状态为银行帐户余额,当前为零。令D表示事件“帐户所有者存入x美元”,而C表示事件“银行用该帐户兑现x美元的支票”。这些事件可能同时发生,但是其中一个会首先影响帐户余额。如果D首先这样做,则净效应为零;否则,净效应为零。但是如果C这样做,则该帐户在存款之前会受到处罚,其净结果是负余额,该余额与退回支票的服务费相对应。在某些情况下,我们实际上必须显式地对同时发生的两个事件的效果进行建模,以完全不同于这两个事件在任一顺序下的发生。
1.3.2 Characteristic Properties of Discrete Event Systems
系统和控制工程中的大多数成功都依赖于基于微分方程的模型,要使用这些数学上方便的模型,系统必须满足两个关键属性:

解读:
1.第一个属性允许我们通过连续变量定义状态,该变量可以采用任何实际(或复杂)值。正是由于这个原因,我们将此类系统称为连续变量动态系统(CVDS)。常见的物理量(例如位置,速度,加速度,温度,压力,流量等)属于此类别。由于我们自然可以为这些连续变量定义导数,因此可以使用微分方程模型。
2.第二个属性指出状态通常随时间变化而变化的事实。结果,时间变量(连续时间为t或离散时间为k)是为此类系统建模的自然自变量。
离散事件动态系统(DEDS)或更广泛地说是离散事件系统(DES)也满足以下两个属性:

离散事件动态系统定义:

Here are some simple examples of discrete-state systems:

注意:1.一类离散时间系统包含CVDS和DES。换句话说,可以像CVDS一样在连续或离散时间内对DES建模。
2.将DES样本路径表示为时序图通常很方便,在事件发生时用箭头表示事件,事件之间显示状态。例如,在图1.23中重画了图1.22的DES采样路径。
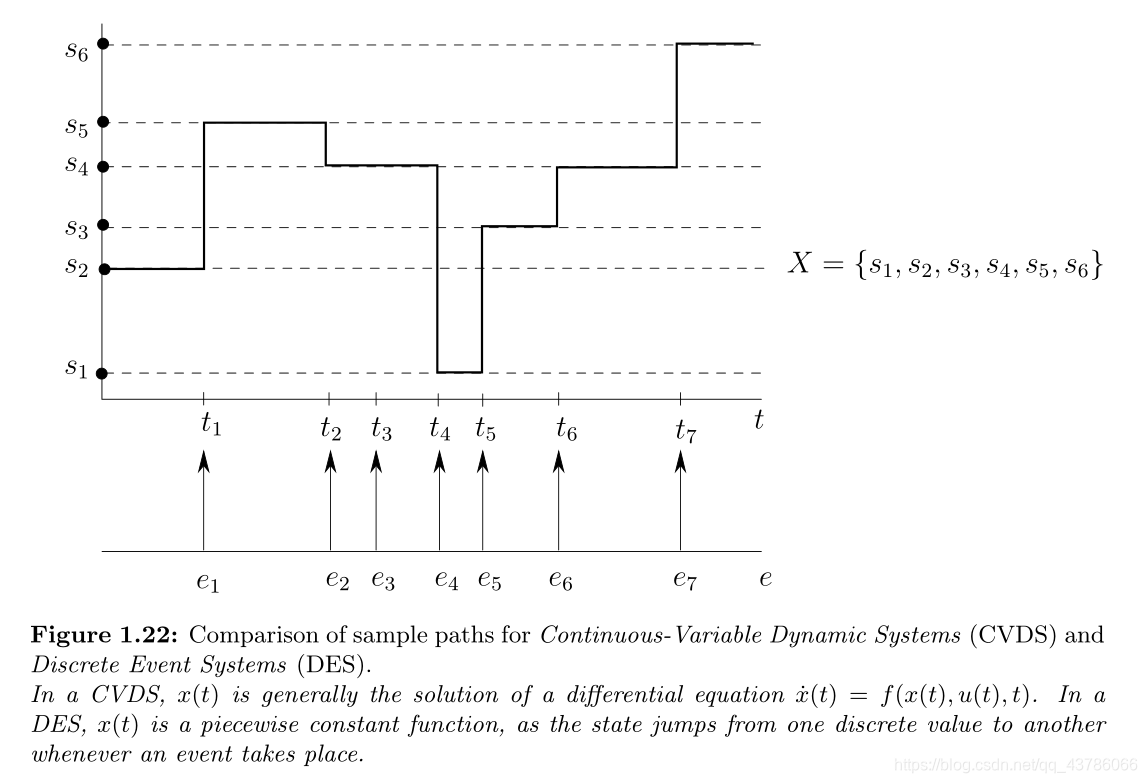
简化为:

1.3.3 The Three Levels of Abstraction in the Study of Discrete Event Systems
系统的定时语言模型
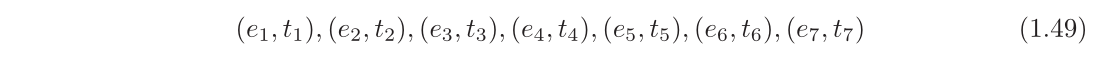
考虑给定系统可以执行的所有定时事件序列的集合。
系统的语言模型
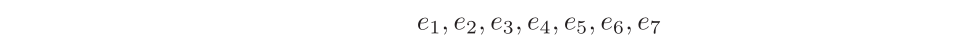
我们可以将事件集E视为“字母”,而将事件的(有限)序列视为“单词”。这是给定系统中所有可能发生的事件排序的集合
系统的随机定时语言模型
该模型列出了所有可能的样本路径以及有关它们的相关统计信息。
注:
1.我们不能忽略DES经常在随机环境下运行的事实,因此必须开发概率模型和相关的分析方法以进行设计和性能分析。在这些情况下,必须考虑系统的随机定时语言模型。
2.这三个抽象级别是互补的,因为它们解决了有关DES行为的不同问题。
3.DES的简介旨在指出这些系统的主要特征。到目前为止,在定义DES时必不可少的两个要素是:离散状态空间(用X表示)和离散事件集(用E表示)。
1.3.4 Examples of Discrete Event Systems
接下来的几小节描述了从现实世界和普通工程经验中获得的DES示例。为了有效地展示这些系统,我们从一个简单的“构建块”开始,它将代表许多感兴趣的DES。
Queueing Systems
一些名词:

模型框图:
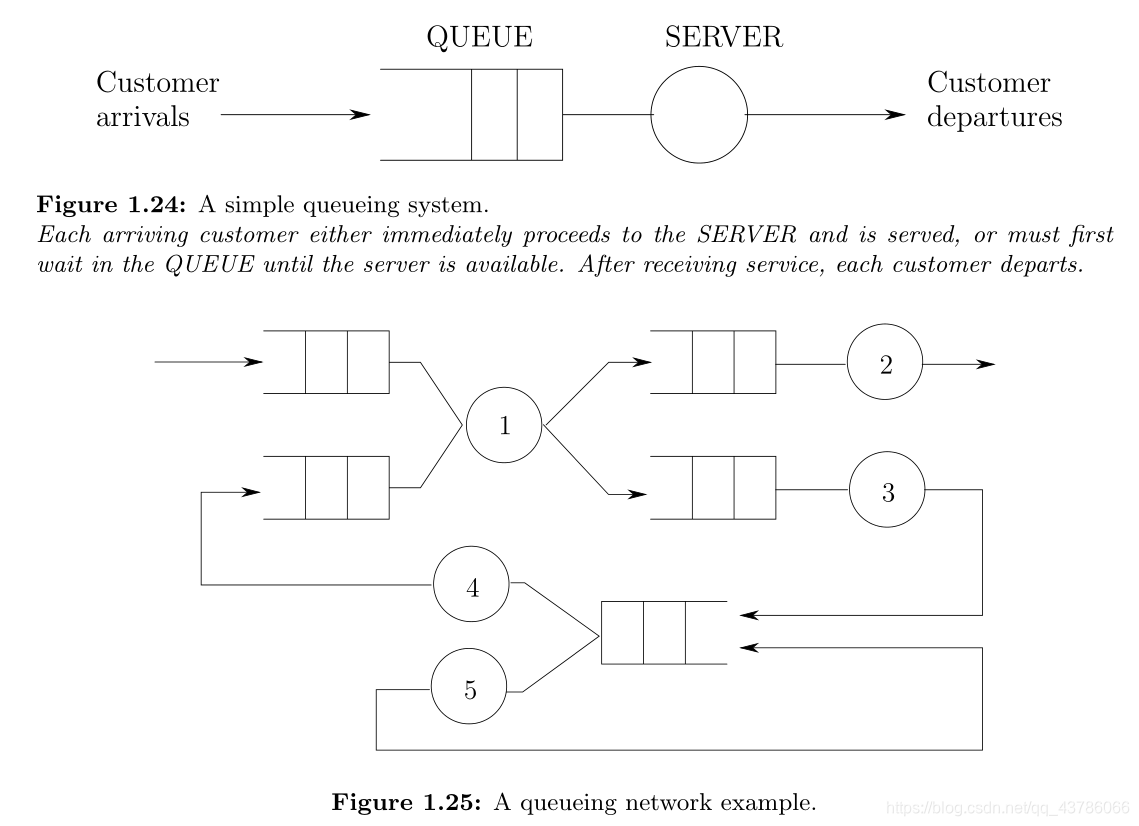
如图1.24所示。圆圈表示服务器,空心框表示该服务器之前的队列。队列中的插槽用于指示等待的客户。客户被认为是到达队列,然后离开服务器。还假设为客户提供服务的过程通常会花费严格的正数(否则就不会等待)。因此,服务器可以被认为是“延迟块”,它在一定的服务时间内保留了客户。
从DES来看,图1.24的排队系统具有事件集E = {a,d},其中a表示“到达”事件,d表示“离开”事件。自然状态变量是队列中的客户数量,我们将其称为队列长度。按照惯例,允许在时间t的队列长度包括在时间t服务的客户。除非另有说明,否则我们将采用该公约。因此,状态空间是一组非负整数X = {0,1,2,…}。
1.3.5 Hybrid Systems
将时间驱动和事件驱动的动力学相结合的系统称为混合系统。
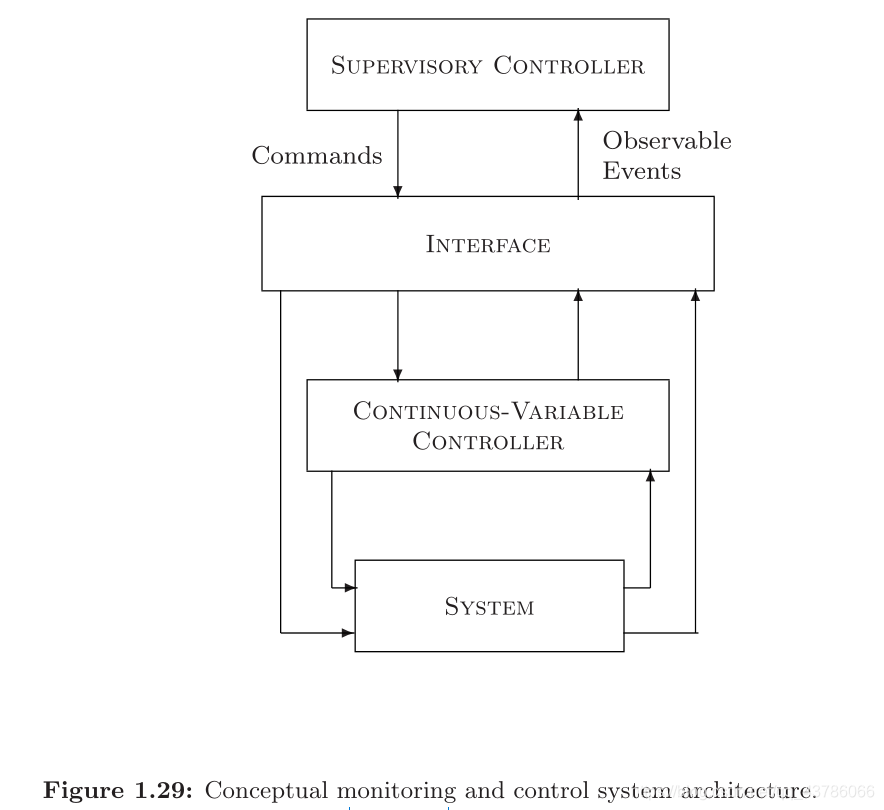
举例:
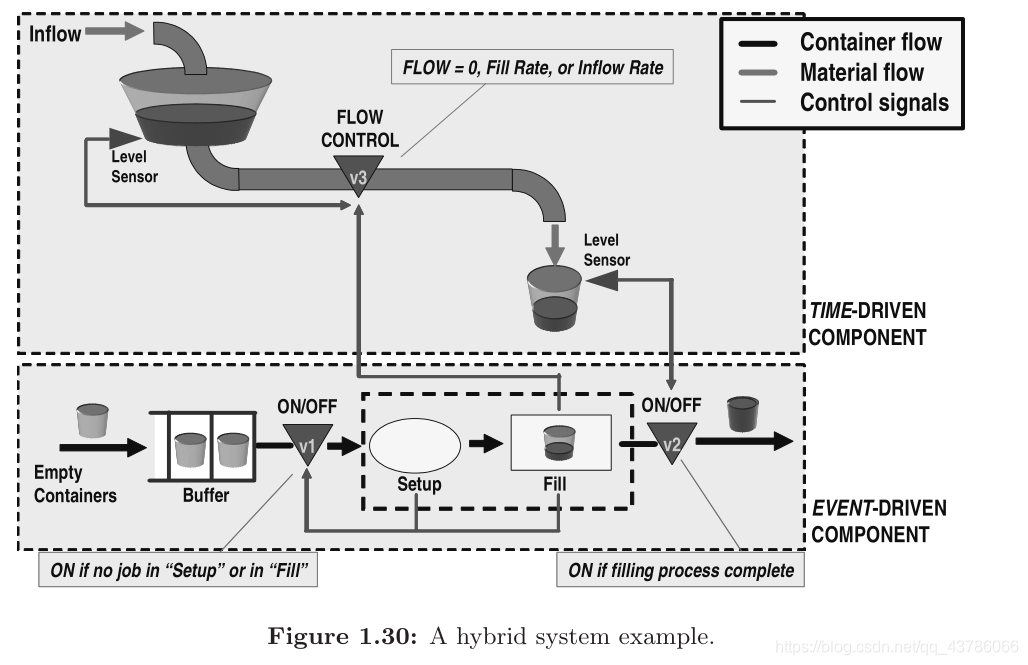
解读:由图1.30中的事件驱动组件描述。空容器在缓冲区中等待,直到填充站可用。发生这种情况时,将打开v1并将容器移动到适当位置以进行填充操作。这需要在加油站之前的设置过程中花费一定的时间。当准备好要装满新容器时,信号将通过v2发送到时间驱动组件,以启动流体的实际流动。填充过程根据时间驱动的动力学进行。流量控制开关v3负责选择适当的流量值:(a)所需的“填充率”,只要容器未满并且供应流体材料的储罐中的液位为正,(b)“流入率” ”对应于流入过程(如果罐是空的),并且(c)当容器装满或没有容器进行灌装操作时为零。注意,该系统包括两个传感器,用于检测:(a)容器何时达到其期望的填充水平;以及(b)何时流体供应箱变空,这会影响流量控制功能。我们可以清楚地看到,在此示例中,事件驱动和时间驱动的组件正在相互作用,从而为此类系统的运行辩称“混合”。
1.4 SUMMARY OF SYSTEM CLASSIFICATIONS

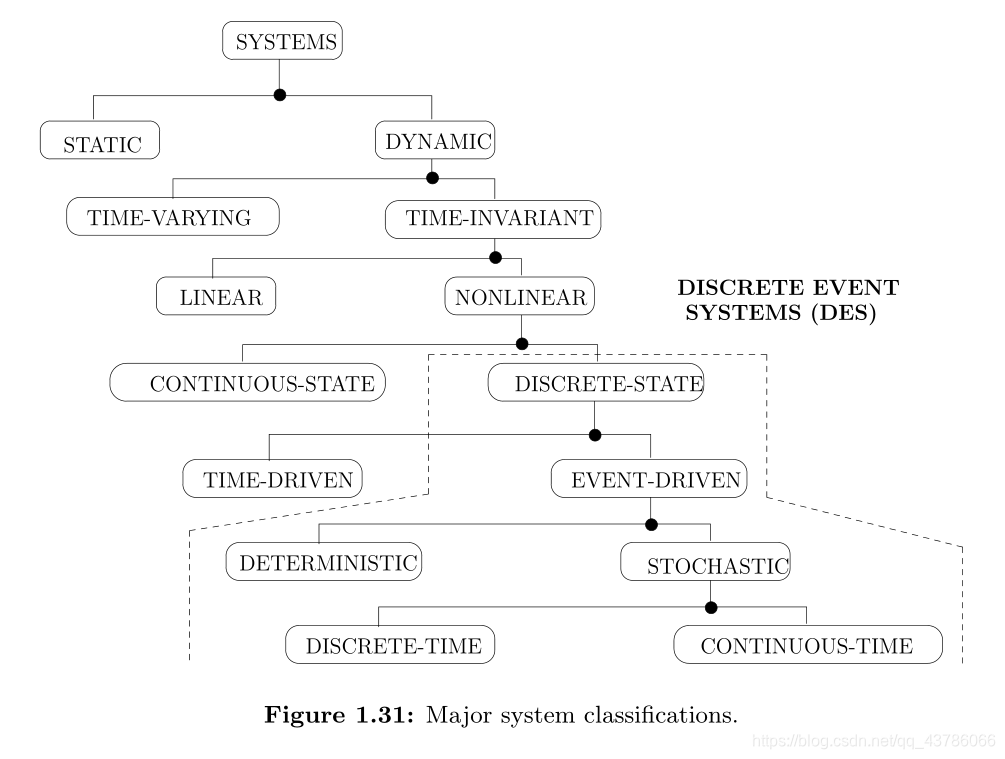

図1.31に示すように、我々はだろうダイナミック、時不変、非線形、離散状態、イベント駆動型システムに焦点を当てます。DESは、非線形イベントが遷移(ジャンプ)固有のすべての状態に不連続に導かれます。DESのカテゴリでは、決定論的または確率的モデルはまた、離散時間または連続時間モデルと考えることができると考えることができます。最後に、のダイナミクスは時間駆動とイベント駆動型が存在、ハイブリッドシステムは、図の下部に表示されることに注意してください。混合システムは、決定論的またはランダムであってもよいし、離散時間または連続時間でモデル化することができます。
1.5システム理論の目的
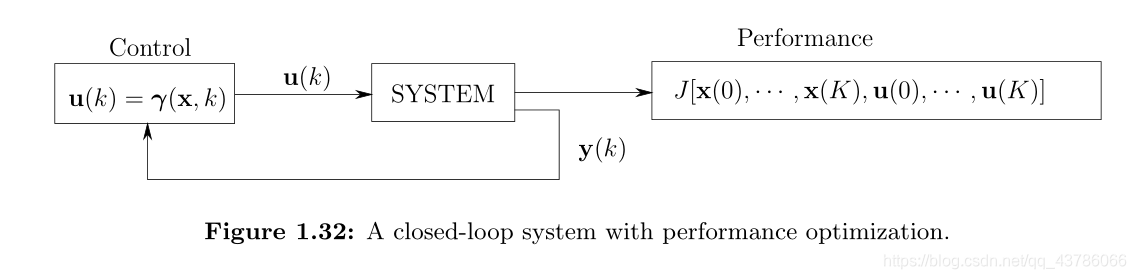
次のように一般的には、私たちのいわゆる客観「システム理論は、」要約することができます。
1.モデリングと解析
2.設計と合成
3.コントロール
4.性能評価
5.最適化を


