Tarjanのアルゴリズム
概念の違い
- 有向グラフ
- 強力な通信：で有向グラフ\（G \）、2つの頂点場合\（（U、U、V \ \ NEQ V）\）は、 から部屋有する\（U \）に\（Vは\）であります経路、ならびにから1 \（V \）に\（U \）と呼ばれる有向パスの、\（U、V \）強連結
- 強いグラフ：場合有向グラフ（G \）\と呼ばれる任意の二つの異なる強連結頂点、\（Gが\）強連結図です。
- 強連結成分：有向グラフ\（G \）最大強連結部分グラフが図呼ば\（G \）は、強連結成分であります
- 無向グラフ
- コミュニケーション：強連結と同様に（だけでなく、数字の任意の側には双方向である場合、（U \ RIGHTARROW V \）\パス、存在する必要があります\（V \ RIGHTARROW U \）のパス）
- 図通信：もし無向グラフ（G \）\と呼ばれる任意の二つの異なる通信頂点、\（Gは\）通信図です。
- ：通信コンポーネント無向グラフ\（G \）は最大図は、サブグラフを接続されたと呼ばれる（G \）\連結成分
- カットポイント（トップカット）：図の非存在下で\（G \） 、削除された点場合\（U \）とで\（U \）すべての側面がエンドポイントである場合、連結成分の数を増加させ、ポイントは言った\（U \）であるカットポイント（カットトップ）
- ブリッジは：無向グラフでは（\ G）\、あなたがエッジを削除した場合\（E =（U、V）\\） （接続\（U、V \）両側後）、図1の通信コンポーネント。エッジと呼ばれる数の増加、（\ E）\のためのブリッジとしても知られる、切刃
- デュアル通信：
- 図二重通信：分割二重図通信により及びエッジデュアル図通信場合、無向グラフ（G \）\任意のノード（片側）を除去するには、図1に変化しない\（G \）接続、すなわち、カット点が存在している図と呼ばれる（ブリッジ）、（G \）\点（エッジ）は、図ビス通信します
- 図両面通信：無向グラフ\（G \）の各極大点ビス接続部分グラフと側通信サブビス図は無向グラフと呼ば\（G \）の通信コンポーネントビス点（BCC）そしてサイドビス通信コンポーネント（E-BCC）
Tarjan
DFSツリー
\（Tarjan \）プロセスのは、実際には、\（DFS \）図のプロセスの\（G \）である\（DFS \）であろう\（DFS \）有向グラフのツリー（\ DFS \）ツリーは、4つの辺有するツリー側、背面側（隔世遺伝側、後方側）、クロスフォーク側及び前方側。バック木の名前が意味するの側、側手段（DFS \）\検索のポイントは、プロセスに訪問されているが、そのサブツリーが完了し、未訪問、横断面のエッジポイントがすでに訪問し、そのサブツリー検索されますアクセスも完了していると、2つの横方向クロスポイントエッジ接続がない先祖と子孫の関係、前縁クロスフォーク側との唯一の違いこと前方側接続の2つの点がある先祖と子孫の関係、読者は組み合わせることができ四辺を理解するには、次の図
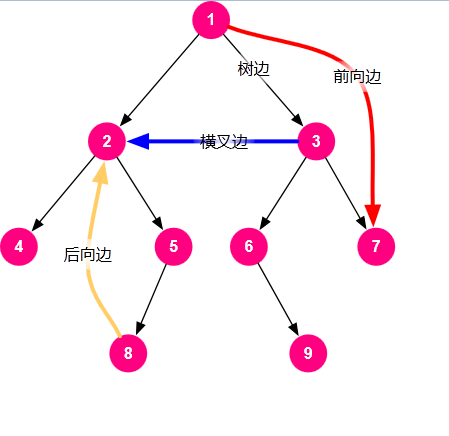
⏫出典：https://www.cnblogs.com/gongpixin/p/5003049.html
強連結成分
思想
\（DFN [U] \） ：頂点\（U \）タイムスタンプアクセスするには、各点\（DFN \）割り当てた後は変更されません
\（低[U] \） ：頂点\（U \）ポイントに到達することができる\（DFN \）ミン
\（スタック[トップ] \）強連結成分の収集ポイントを構成してもよいです。
\（VIS [U]：\ ） 頂点\（U \）は、スタックにあります
\（色[U] \） ：頂点（U \）\異なる色、強連結成分を識別するため
いくつかのトピックを追加// \（色\）配列は、より便利であることが必要ではありません
すべての可能な強連結成分のための思考の深さ優先探索は、実行\（DFS \）のコレクションを維持することが強連結成分を構成することができる：\（スタックを\） 、ポイントが追加検索（\スタック）\、およびその維持\（DFN、\ VIS \）値、バックを維持しつつ、エッジによって接続された頂点をダウン検索\（低\）ポイント場合、値を\（U \） A \（DFN ==低い\ ）それは木の強連結成分のサブルートであることを、我々は長い間、スタックなどとして、強連結成分を発見した\（スタック\）それが飛び出すまで、ポップアップポイントで\（U \）
- 同じ点で強連結成分\（低\）の値は同じです
ここを参照してください、一部の読者は、あなたがたはありません接続されたコンポーネントをお願いするもの、求めることができますか？また、直接設定します（tarjan \）\ボードのですか？あなたは、このような混乱を持っている場合とにかく、私が持っていましたそれは愚かな学習するアルゴリズムを学んでいますノーまた、無向グラフ\（tarjan \）何直接\（DFS \）または\（BFSは\）再び思慮深い読者は、なぜ無向グラフ便利なように依頼することが、完成するのでしょうか？そのため無向グラフのため、パスがあれば\（U \ RIGHTARROW V \） 、およびパスその\（V \ RIGHTARROW U \）存在している必要があり、\（uは\）のみポイントを得ることができます（を含む\（U \）そのもの）連結成分であります
ボード
void tarjan(int u) {
dfn[u] = low[u] = ++tim;
vis[u] = true; // 入栈
stack[++top] = u;
int size = g[u].size();
for(int i = 0; i < size; ++i) {
int v = g[u][i];
if(!dfn[v]) { // 树边，继续下搜
tarjan(v);
low[u] = min(low[u], low[v]);
} else if(vis[v]) // 回边，更新low[u]
low[u] = min(low[u], dfn[v]);
}
if(dfn[u] == low[u]) {
color[u] = ++sum;
vis[u] = false;
while(stack[top] != u) {
color[stack[top]] = sum;
vis[stack[top--]] = false;
}
top--;
}
}
//for(int i = 1; i <= n; ++i)
// if(!dfn[i])
// tarjan(i);カットポイント（トップ）/ブリッジ
原則
で\（tarjan \）主にエッジの二種類に関連するカットポイントの処理アルゴリズム、：ツリー側と背面側（隔世遺伝側）、上記で意味⏫
定理\（1 \） ：無向グラフでは（G \）\、点\（uは（uがルートではない）\）のカット点である\（\ IFF \） \（U \）サブツリーの\（ Tは、\）リターンが含まれていない（U \）\祖先を含む（ではない（U \ \） ）エッジ\（\ IFF \） \（低[V]> = DFN [U] \）
具体的には、ルート・ノードは、トップカットである\（\ IFF \）子ノードのその数がより大きい（1 \）\
約YYペイント：
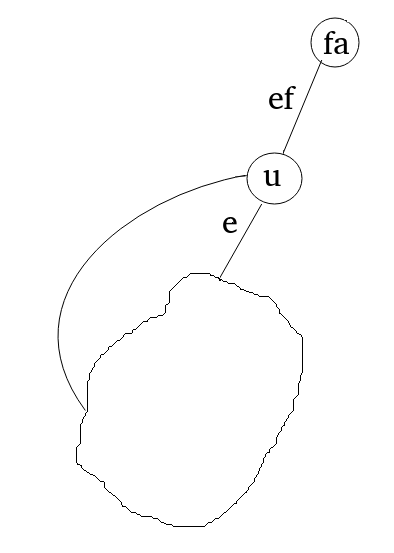
地図上の\（uが\）サブツリーです\（Tは\）が返されますが、\（U \）背面側の、しかし戻らなかった\（U \）の祖先（含まれていません（\ uと\） ）の背面側ので、\（U \）は、ポイントカットが、エッジである\（eは\）ブリッジではありません
定理\（2 \） ：無向グラフで\（G \） 、エッジ\（（u、v）は\ ） ブリッジである\（\ IFF \） \（U \）サブツリーの\（T \）リターンが含まれていない\（U \）祖先（含む\（U \） ）エッジ\（\ IFF \） \（低[V]> DFN [U] \）
表示またはの前に、\（faが\） 、サブツリーはリターンが含まれていないです\（FA \）の祖先（含む\（FA \）ので、）背面側を\（EFは\）ブリッジがあります
可以看出如果一个图\(G\)有桥，它必有割点，因为桥连接的两端必然至少有一个是割点，但反过来不成立
板子
还有点细节：
\(child\)是点\(fa\)的子节点个数，注意\(fa\)的孙子不计算在内
特别的，像：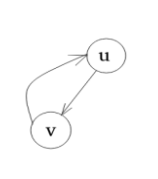
，点\(u\)不是割点，因为去掉它后，这个图的强连通分量的个数并没有增加
void Tarjan(int u, int fa) { // 割点
low[u] = dfn[u] = ++tim;
int sz = g[u].size(), child = 0;
for(int i = 0; i < sz; i++) {
int v = g[u][i];
if(!dfn[v]) {
Tarjan(v, fa);
low[u] = min(low[v], low[u]);
if(low[v] >= dfn[u] && u != fa) iscut[u] = true;
// if(low[v] > dfn[u]) u - v 是桥
if(u == fa) child++;
} else
low[u] = min(low[u], dfn[v]);
}
if(fa == u && child >= 2) iscut[u] = true;
}
//for(int i = 1; i <= n; ++i)
// if(!dfn[i])
// tarjan(i, i);缩点
啥是缩点
就把一个强连通分量(或边双连通分量等，视题目而定)缩成一个点
再看张图YY一下：
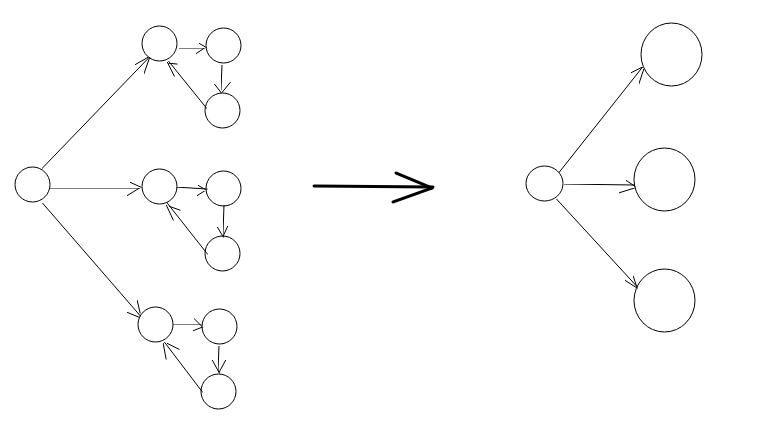
光这么讲，大家肯定还是云里雾里，这缩点到底能干啥？下面我们通过两道例题来看看缩点到底能干啥
例题
-
思路：缩点，把一个强连通分量缩成一个点，新点的权值等于强连通分量里的所有点的点权之和，缩完点就能得到一个有向无环图\((DAG)\)，然后就可以在这个\(DAG\)上跑\(dp\)了，然后就能得到答案
双连通分量
一点性质
- 边双连通分量(e-BCC)满足任意两点间都有至少两条边不重复的路径
- 点双连通分量(BCC)满足任意两点间都有至少两条点不重复路径
- 有桥必有割点，一个点双连通分量必然是边双连通分量，反之，不一定成立
边双连通分量(e-BCC)
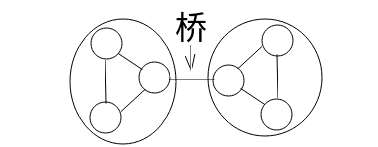
如上图，左右两个用大圈圈出来的分别是两个边双连通分量
求法：
ブリッジは、残りのすべてのコンポーネントがあれば、再びとして、独立した両面接続コンポーネントである削除する\（\ tarjan）がブリッジを見つけるために、再度\（DFS \）エッジを得ることができる連結成分を倍増することができるであろう
ビスポイント通信コンポーネント（BCC）
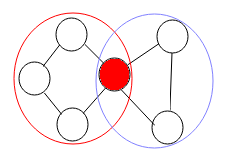
上記のように、円の左側と紫色に赤い円が通信デュアル成分の二点である、赤い点は、全体図のカット点です。
ビス二点多くても1つの共通点コンポーネント間の通信、およびそれがカットポイントである必要があり、二点通信の特定の成分に属していないカット頂点
探しています：
限り分離のカットポイントとして、分離点があろう連結成分を、ビスが、カットポイントが2つの二重点連結成分に属することができ、それは一般的にコンポーネントの出力側で使用され、それが一度横断スタックエッジに保存することができカッティングエッジがBCCに属するの上にポップアップ表示ことがわかりました
例
-
アイデア：質問の意味は、少なくともいくつか尋ねたプラスの側面は、マップ全体が、少なくとも間の全体マップ内の任意の2点を持つことができるエッジの数を増やし、少なくとも頼まれるダブルエッジの接続となり、作ることができる2つの私たちは、非繰り返しのパスの両側従来の両面通信コンポーネントは、ツリーを構成するエンドポイントを縮小、凝縮点であってもよいです。それが完了凝縮点後の図ビス通信ツリー内のいくつかの側面のエッジを追加することが可能となるように、今、被写体が最小となる、無向ツリーの結論は、それは、私たちのダブルエッジ接続グラフになること（+1度1のツリーのポイント数）/ 2追加する辺の数=