绝对值函数
の$ Y = \左| X \右| =
\左\ {\開始{行列}
X、X \ GE 0 \\
-X、X <0
。\端{行列} \右$
自然:
左$ \ | X \権| = X \ Leftrightarrow X \ \左GE 0、| X \権| = -x \ Leftrightarrow X \ル0 $
グラフィックス:

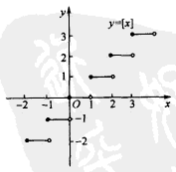
関数丸め
= [X] = $以下$ X $に等しい最大の整数をさ$ yを
区分関数によって表される:[X] = $のY = N、N \ルX <N + 1 $($ N $は整数です。 )
自然:
$ [X] \ルX <[X] + 1、[X] = X \ Leftrightarrow X $整数、$の[X + Y] \ GE [X] + [Y]、[X + N] = [X ] + N $($ N $は整数です)
グラフィック:(ステップカーブ)
符号函数
の$ Y = sgnx =
\左\ {\ {行列}始める
0 \\> X&、1を
0、&x = 0の\\
X <0、-1
右\ \端{行列} $
性质:
$ sgnx = 1 \ Leftrightarrow X> 0、sgnx = -1 \ Leftrightarrow X <0 $
$ SGN(XA)= 1 \ Leftrightarrow X>、SGN(XA)-1 \ Leftrightarrow X <$の=
$ xを= sgnx \ CDOT \左| X \権| X \右| | = sgnx \ CDOTのx $、\左
グラフィックス:

ディリクレ関数
$ Y = D(X)=
\左\ {\開始マトリックス{}
。1、有理数X&\\である
0、Xが無理数となる
右\ \端{行列} $
特性:
ディリクレ関数は、多くの悪い性質を有する
1)は、グラフィックディリクレ関数(NO曲線セグメント)
周期関数の周期で2)nはディリクレ関数は、それは正の最小周期の有理数でありません
3制限なくどこでも)ディリクレ関数ではなく、どこにでも連続的な、常に非導通、任意の間隔で非積分
特定の品質機能を有するトランス構成および実施形態を与えるために使用ディリクレ関数
関数のとして:$ yは= XDの(X) $だけ連続し、原点に他の点で不連続
関数$ Y = X ^ {2} $(x)はD 他の点で間欠的に(したがって、非導電性)だけ原点になってもよいです
注意:
ディリクレ関数は、$ Dの限界(X)= \ lim_ {M \のRIGHTARROW用の\ inftyの} [\ lim_ {N \ RIGHTARROW \ inftyの} COS ^ {N}(\パイM!X)] $として定義することができます