目次
クロスエントロピーの簡単な理解: 実分布と非実分布の交差、完全に対応、エントロピーは 0
クロスエントロピーの簡単な理解: 実分布と非実分布の交差、完全に対応、エントロピーは 0

この式はエントロピーを表すもので、簡単に言えば、最適化戦略に基づいて色を推測するために必要な質問の数を意味します。エントロピーは、確率変数またはシステム全体の不確実性を表し、エントロピーが大きいほど、確率変数またはシステムの不確実性も大きくなります。
エントロピーとは何かを理解したので、クロス エントロピーの意味を説明しましょう。2 番目の例では、以下に示すように、最初の例の戦略を引き続き使用するとします。

確率 1/8 の場合、コインはオレンジ色であり、2 つの質問が必要です。確率 1/2 の場合、青の場合でも、2 つの質問が必要です。つまり、ボールの分布は (1/4, 1/4, 1/ 4、1/4)、この分布は真の分布ではありません。平均して必要な問題数は、1/8×2+1/8×2+1/4×2+1/2×2=2 となります。したがって、例 2 で例 1 の戦略を使用することは、比較的貧弱な戦略です(2 は、このスキームのクロスエントロピーです)。最適解のクロスエントロピーは 1.75 です。
戦略が与えられると、クロスエントロピーは、その戦略に基づいて色を推測するために必要な問題の期待値になります。より一般的には、クロスエントロピーは、特定の実数分布の下で非実数分布によって指定された戦略を使用してシステムの不確実性を排除するコストを測定するために使用されます。
クロスオーバーの文字通りの意味は、実分布と非実分布の交差です。計画があれば、戦略が優れているほど、最終的なクロスエントロピーは低くなります。クロスエントロピーが最も低い戦略が最適な戦略であり、上で定義したエントロピーです。したがって、機械学習では、クロスエントロピーを最小限に抑える必要があります。完全に一致し、エントロピーは 0 です
このうち、p は実確率で、例 2 ではオレンジと緑が 1/8、赤が 1/4、青が 1/2 となります。p^ は誤って仮定された確率です。たとえば、例 2 では、すべての色の確率が 1/4 であると誤って仮定されました。p と p^ は少し混乱するかもしれません。log は戦略に基づいて推測するために必要な質問の数を計算するために使用されるため、log に必要なのは予測確率 p^ であることを覚えておいてください。決定木では、確立された木が最適でない場合、その結果は出力の確率分布の仮定が間違っていることになり、直接的な結果としてクロスエントロピーが高くなります。クロスエントロピーは決定木だけでなく、他の分類問題でも使用されます。
分類問題
二項分類問題では、ラベル y が 1 である尤度はラベル y の予測 y^ であり、同様に、ラベルが 0 である尤度は 1y^ です。尤度関数を最大化する必要があります。二項分類問題の特異性、ベルヌーイ分布によれば、尤度関数は次のように書くことができます。
y=1 の場合、第 2 項は 1 であるため、最適化は y^ となります。
y=0 の場合、最初の項目は 1 で、最適化は 1y^ です。上記の尤度関数の対数を取ると、結果は次のようになります。
尤度関数を最大化するとは、上記の式の負の値を取り、それを最小化することです。これはクロスエントロピーの表現でもあります。クロスエントロピーは、対数損失関数と呼ばれることもあります。上の例との違いは、余分な負の符号があることに注意してください。上の例は不確実性を除去するためのコストであり、負の符号が付いたクロス エントロピーが最終的な目的関数になります。
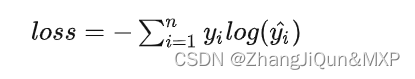
たとえば、正と負の 3 つのコインがあり、1、1、0 と記録されているとします。予測結果は 0.8、0.9、0.3 であるため、クロス エントロピーの平均値は次のようになります。
1/3(1×log0.8+1×log0.9+(10)×log(10.3))
1、1、0 を直接予測する完全なアルゴリズムがあると仮定すると、クロス エントロピーの結果は 0 になります。