前回の記事に引き続き、バッチサイズが 1 なので損失が大きく変動しますが、今回はバッチサイズが 1 より大きい場合について説明します。バッチサイズの数が N の場合、y = wx + by=wx+by=w ×+bの失関数は次のとおりです。
L = ∑ i = 1 N ( wxi ∗ + b − yi ∗ ) 2 = ( wx T + be T − y T ) ( wx + be − y ) \begin{aligned} L&=\sum_ {i=1}^{N}(wx_i^*+b-y_i^*)^2\\ &=(w\boldsymbol{x}^T+b\boldsymbol{e}^T-\boldsymbol{y} ^T)(w\boldsymbol{x}+b\boldsymbol{e}-\boldsymbol{y}) \end{aligned}L=i = 1∑N( w x私∗+b−y私∗)2=( w xT+ありますT−yT )(wx+あります−y )
計算の便宜上、損失関数には極値に影響を与えずに値が乗算され、損失関数は次のようになります。
L = 1 2 ∑ i = 1 N ( wxi ∗ + b − yi ∗ ) 2 L=\frac{ 1} {2}\sum_{i=1}^{N}(wx_i^*+b-y_i^*)^2L=21i = 1∑N( w x私∗+b−y私∗)2
見つけましたwwwとbbbの勾配:
∂ L ∂ w = ∑ i = 1 N ( wxi ∗ + b − yi ∗ ) xi ∗ = ∑ i = 1 N wxi ∗ 2 + ∑ i = 1 N bxi ∗ − ∑ i = 1 N yi ∗ xi ∗ = wx T x + be T x − y T x = ( wx T + be T − y T ) x \begin{aligned} \frac{\partial{L}}{\partial{w}}&=\ sum_{i=1}^{N}(wx_i^*+b-y_i^*)x_i^*\\ &=\sum_{i=1}^{N}wx_i^{*2}+\sum_{i =1}^{N}bx_i^*-\sum_{i=1}^{N}y_i^*x_i^*\\ &=w\boldsymbol{x}^T\boldsymbol{x}+b\boldsymbol{ e}^T\boldsymbol{x}-\boldsymbol{y}^T\boldsymbol{x}\\ &=(w\boldsymbol{x}^T+b\boldsymbol{e}^T-\boldsymbol{y} ^T)\boldsymbol{x} \end{整列}∂w _∂L _=i = 1∑N( w x私∗+b−y私∗) ×私∗=i = 1∑Nw ×私※ 2+i = 1∑Nbx _私∗−i = 1∑Ny私∗バツ私∗=w ×T ×+ありますT ×−yT ×=( w xT+ありますT−yT )x
∂ L ∂ b = ∑ i = 1 N ( wxi ∗ + b − yi ∗ ) = ( wx T + be T − y T ) e \begin{aligned} \frac{\partial{L}}{\partial{b }}&=\sum_{i=1}^{N}(wx_i^*+b-y_i^*)\\ &=(w\boldsymbol{x}^T+b\boldsymbol{e}^T-\ボールドシンボル{y}^T)\ボールドシンボル{e} \end{整列}∂b _∂L _=i = 1∑N( w x私∗+b−y私∗)=( w xT+ありますT−yて)え
ここで、x \boldsymbol{x}xは各バッチのすべてのx ∗ x^*ですバツ∗ はN 次元の列ベクトルy \boldsymbol{y}yは各バッチのすべてy ∗ y^*y∗ , e \boldsymbol{e}で構成される N 次元の列ベクトルeは長さ N の列ベクトルです。 **ベクトル表現を使用すると、numpy を使用して回帰プロセスを簡単に実装できます。**Python を使用すると、次の結果が得られます。
import numpy as np
import random
import matplotlib.pyplot as plt
x = np.array([0.1,1.2,2.1,3.8,4.1,5.4,6.2,7.1,8.2,9.3,10.4,11.2,12.3,13.8,14.9,15.5,16.2,17.1,18.5,19.2])
y = np.array([5.7,8.8,10.8,11.4,13.1,16.6,17.3,19.4,21.8,23.1,25.1,29.2,29.9,31.8,32.3,36.5,39.1,38.4,44.2,43.4])
print(x,y)
plt.scatter(x,y)
plt.show()
散布図は次のとおりです。
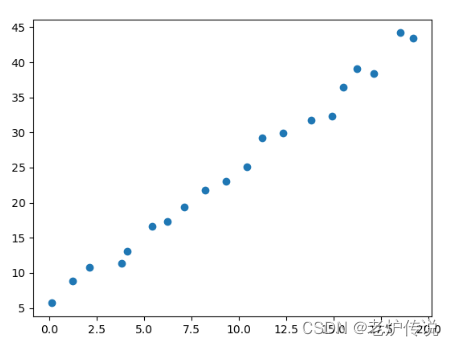
回帰プロセスでは、numpy の行列計算を使用して、上記の損失関数と勾配に従って直接計算します。
# 设定步长
step=0.001
# 存储每轮损失的loss数组
loss_list=[]
# 定义epoch
epoch=500
# 定义batch_size
batch_size=18
# 定义单位列向量e
e=np.ones(batch_size).reshape(batch_size,1)
# 定义参数w和b并初始化
w=0.0
b=0.0
#梯度下降回归
for i in range(epoch) :
#计算当前输入x和标签y的索引,由于x和y数组长度一致,因此通过i整除x的长度即可获得当前索引
index = i % int(len(x)/batch_size)
# 当前轮次的x列向量值为:
cx=x[index*batch_size:(index+1)*batch_size]
cx=cx.reshape(len(cx),1)
# 当前轮次的y列向量值为:
cy=y[index*batch_size:(index+1)*batch_size]
cy=cy.reshape(len(cy),1)
# 计算当前loss
curloss = (w*cx.T+b*e.T-cy.T).dot((w*cx+b*e-cy))
loss_list.append(float(curloss))
# 计算参数w和b的梯度
grad_w = (w*cx.T+b*e.T-cy.T).dot(cx)
grad_b = (w*cx.T+b*e.T-cy.T).dot(e)
# 更新w和b的值
w -= step*grad_w
b -= step*grad_b
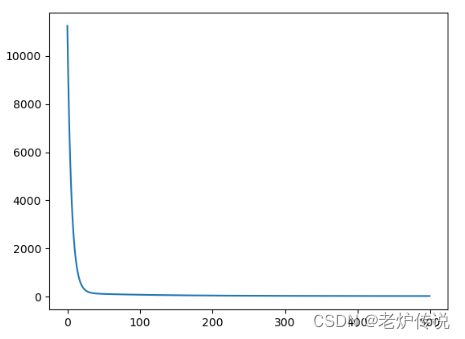
損失関数と最終的なフィッティング結果は次のとおりです。
print(loss_list)
plt.plot(loss_list)
plt.show()
pred_y = w*x+b
plt.scatter(x,y)
plt.plot(x,pred_y.reshape(len(x)),c='r')
plt.show()
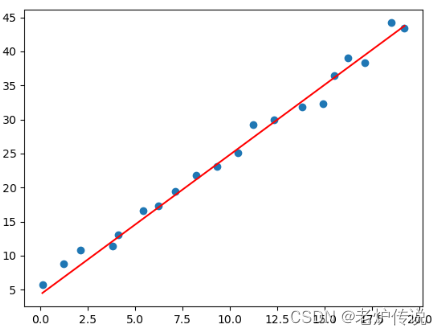
バットサイズを大きくした後、損失関数が比較的安定していることがわかります。