状態推定器

開発 2023-07-02 08:59:33 訪問数: null

記事ディレクトリ

1. 状態空間モデル

  • IMU: 加速度計 + ジャイロスコープ、6 軸データを測定

1.1. 連続状態空間モデル

  • 時間連続の固定長線形システム{ x ˙ ( t ) = A cx ( t ) + B cu ( t ) y ( t ) = C cx ( t ) \left\{\begin{matrix} \dot{ \bm x}(t)={\bm A}_c{\bm x}(t)+{\bm B}_c{\bm u}(t) \\ {\bm y}(t)= {\ bm C}_c{\bm x}(t) \end{行列}\right.{ バツ˙ (t)=あcx (t)+Bcu (t)y (t)=Ccx (t)
    • x ( t ) {\bm x}(t)x (t): システム      \;\; u ( t ) {\bm u}(t)u (t): 制御ベクトル      \;\; y ( t ) {\bm y}(t)y (t): 出力ベクトル
    • A c {\bm A}_cあc: システム行列      \;\; B c {\bm B}_cBc: 入力行列      \;\; C c {\bm C}_cCc: 出力行列
    • 意味: 次の段階におけるシステムの変化 x ˙ ( t ) \dot{\bm x}(t)バツ˙ (t)とシステムの現在の状態x ( t ) {\bm x}(t)x (t)、システムは現在u ( t ) {\bm u}(t)u (t); システム出力y ( t ) {\bm y}(t)y (t)とシステム状態x ( t ) {\bm x}(t)x (t)は以下に関連しています
  • 状態量x \bm xを推定する必要があるx : ワールドシステム {s} におけるロボットの運動状態
    • 機体位置pb {\bm p}_bpb、機体速度vb {\bm v}_bvb、4 つの足の位置p 0 p 1 p 2 p 3 {\bm p_0}\;{\bm p_1}\;{\bm p_2}\;{\bm p_3}p0p1p2p3、すべて 3 次元ベクトルなので、x \bm xxは 18 次元ベクトルです
      • x = [ pbvbp 0 p 1 p 2 p 3 ] x=\begin{bmatrix} {\bm p}_b \\ {\bm v}_b \\ {\bm p_0} \\ {\bm p_1} \\ { \bm p_2} \\ {\bm p_3}\end{bmatrix}バツ= ​pbvbp0p1p2p3​ ​
    • 状態ベクトル ˙ \dot{\bm x} の導関数 x を考えます。バツ˙、4 つの足の端が地面と安定して接触していると仮定すると、各足の端の速度はゼロになります。
      • x ˙ = [ vb R sbab + g 0 3 × 1 0 3 × 1 0 3 × 1 0 3 × 1 ] \dot{x}=\begin{bmatrix} {\bm v}_b \\ {\bm R} _{sb}{\bm a}_b+{\bm g} \\ {\bm 0}_{3\times1} \\ {\bm 0}_{3\times1} \\ {\bm 0}_{ 3\times1} \\ {\bm 0}_{3\times1} \end{bmatrix}バツ˙= ​vbRs bあるb+g03 × 103 × 103 × 103 × 1​ ​
  • 測定可能な出力:
    • IMU によって測定された機体姿勢R sb \bm R_{sb}Rs b, {b}のab , ω b \bm a_b\;,\;\bm\omega_bあるb、おおb;
    • 機体に対する{b}下足の位置pbf B {\bm p}_{bfB} は、各関節エンコーダと順運動学から取得されます。pb f Bそしてpsf B {\bm p}_{sfB} / {s}psfB _ _;
    • {s} の足から体までの速度vsf B \bm v_{sfB}vsfB _ _;
    • 残りの 4 つの足はすべて地面に触れており、高さは 0 です。
  • 出力ベクトルy \bm yy、28 次元ベクトル
    • y = [ psf B 0 psf B 1 psf B 2 psf B 3 vsf B 0 vsf B 1 vsf B 2 vsf B 3 psz 0 psz 1 psz 2 psz 3 ] \bm y=\begin{bmatrix} {\bm p} _{sfB0} \\ {\bm p}_{sfB1} \\ {\bm p}_{sfB2} \\ {\bm p}_{sfB3} \\ {\bm v}_{sfB0} \\ {\bm v}_{sfB1} \\ {\bm v}_{sfB2} \\ {\bm v}_{sfB3} \\ p_{sz0} \\ p_{sz1} \\ p_{sz2} \ \ p_{sz3} \end{bmatrix}y= ​psfB0 _ _ _psfB1 _ _ _psfB2 _ _ _psfB3 _ _ _vsfB0 _ _ _vsfB1 _ _ _vsfB2 _ _ _vsfB3 _ _ _pサイズ0pNo.1 _pNo.2 _pNo.3 _​ ​

1.2. 離散状態空間モデル

  • プログラムは、離散システムと呼ばれる間隔でデータをサンプリングする必要があり、kkで表される、対応する離散状態空間モデルを使用する必要があります。k は k番目の瞬間を意味します
    • { x ˙ ( k ) = A x ( k − 1 ) + B u ( k − 1 ) y ( k ) = C x ( k ) \left\{ \begin{matrix} \dot{\bm x}(k )={\bm A}{\bm x}(k-1)+{\bm B}{\bm u}(k-1) \\ {\bm y}(k)={\bm C}{ \bm x}(k)\end{行列}\right。{ バツ˙ (k)=A × (k−1 )+これは__です−1 )そして(k)=C x (k)

2. 行列微積分

  • 二次形式の偏微分計算
    • ∂ x TA x ∂ x = x TAT + x TA \frac{\partial{\bm x}^{\rm T}\bm A x}{\partial \bm x}=\bm x^{\rm T} \bm A^{\rm T}+\bm x^{\rm T}\bm A∂ ×∂ ×税金__=バツTA _T+バツTA _
      • 対称行列の場合、A = AT \bm A=\bm A^{\rm T}あ=あT有∂ x TA x ∂ x = 2 x TA \frac{\partial{\bm x}^{\rm T}\bm A x}{\partial \bm x}=2\bm x^{\rm T }\bmA∂ ×∂ ×税金__=2倍_TA _
  • 行列ベクトル積の部分導関数
    • ∂ A x ∂ x = A ∂ x TA ∂ x = AT \begin{行列} \frac{\partial\bm A\bm x}{\partial \bm x}=\bm A \\ \frac{\partial\ bm x^{\rm T}\bm A}{\partial \bm x}=\bm A^{\rm T} \end{行列}∂ ×∂Ax _ _=あ∂ ×∂ ×TA _=あT
  • マトリックスの跡
    • ∂ T r ( ABAT ) ∂ A = ABT + AB \frac{ \partial {\rm Tr}(\bm A\bm B\bm A^{\rm T})}{\partial \bm A}=\bm A\bm B^{\rm T}+\bm A\bm B∂A _∂ Tr ( A B Aた）=AB _T+AB _
      • 対称行列の場合、A = AT \bm A=\bm A^{\rm T}あ=あT有∂ T r ( ABAT ) ∂ A = 2 AB \frac{ \partial {\rm Tr}(\bm A\bm B\bm A^{\rm T})}{\partial \bm A}=2 \bm A\bm B∂A _∂ Tr ( A B Aた）=2 AB _

3. 二次プログラミング

  • 二次計画法 (QP) は最適化問題で広く使用されており、カルマン フィルターは最適状態推定の一種です。
    • 对y = ax 2 + bx + cy=ax^2+bx+cy=× _2+bx _+cの最大値を見つけるにはy ˙ = 2 ax + b = 0 \dot{y}=2ax+b=0 とy˙=2 × _+b=0
  • コスト関数 J をスカラーとして定義します。J = x TA x + bx + c J=\bm x^{\rm T}\bm A \bm x+\bm b \bm x + cJ=バツTAX __+bx _+c
    • 设A \bm AAは対称行列、正定行列、偏微分∂ J ∂ x = 2 A x + b = 0 \frac{\partial J}{\partial \bm x}=2\bm A\bm x+\bm b= 0∂ ×∂ J=2A × _+b=0
    • JJのときJ は最小値x = − 1 2 A − 1 b \bm x=-\frac{1}{2}\bm A^{-1}\bm b をバツ=−21あ− 1 b、二次計画法の理論的解

正定行列A \bm AA、ゼロ以外のベクトルv \bm vv , 有v TA v > 0 \bm v^{\rm T}\bm A\bm v>0vTAV __>0

4. 確率論

4.1. 期待と差異

  • 期望 E ( x ) \bm E(x) E (x)またはx ‾ \overline{x}バツ： 平均
    • E ( x + y ) = E ( x ) + E ( y ) E(x+y)=E(x)+E(y)そして( x+y ）=E ( × )+E (および)
  • 分散σ x 2 \sigma_x^2pバツ2確率変数xxを説明してくださいxと予想されるx ‾ \overline{x}バツ分散度
    • σ x 2 = E [ ( x − x ‾ ) 2 ] \sigma_x^2=E[(x-\overline{x})^2]pバツ2=そして[( x−バツ)2 ]
  • 表現: x 〜 ( E ( x ) , σ x 2 ) x\sim (E(x),\sigma_x^2)バツ〜( E ( x ) 、pバツ2)

4.2. 独立したイベント

  • 协方差C xy = E [ ( x − x ‾ ) ( y − y ‾ ) ] C_{xy}=E[(x-\overline{x})(y-\overline{y})]Cｘｙ=そして[( x−バツ) ( y−y​)]
  • 1 つのイベントの発生が別のイベントの確率に影響を及ぼさない場合、2 つのイベントは独立したイベントであり、それらの共分散C xy = 0 C_{xy}=0Cｘｙ=0

4.3. ベクトル確率変数

  • 行列の期待値は、行列の各要素の期待値を個別に見つけることです
  • 確率変数x y \bm x\;\bm yバツ共分散行列C xy = E [ ( x − x ‾ ) ( y − y ‾ ) T ] \bm C_{xy}=E[(\bm x-\overline{\bm x})(\bm y -\上線{\bm y})^{\rm T}]Cｘｙ=そして[( x−バツ) ( y−y​)た]
    • C xy \bm C_{xy}Cｘｙ対称配列
  • 確率変数x \bm xxとその共分散行列C x = E [ ( x − x ‾ ) ( x − x ‾ ) T ] \bm C_{x}=E[(\bm x-\overline{\bm x})(\ bm x-\overline{\bm x})^{\rm T}]C×=そして[( x−バツ) ( ×−バツ)た]
    • C x \bm C_xC×は対称行列、対角要素は確率変数x \bm xxの各項の分散
    • 若x \bm xxの項は互いに独立しているため、共分散行列C x \bm C_xC×は対角行列であり、非対角要素は 0 です。

4.4. ノイズと共分散行列

  • ホワイトノイズ: t 1 t_1t1時間ノイズ ベクトルv ( t 1 ) \bm v(t_1)v ( t1)とt 2 t_2t2時間ノイズ ベクトルv ( t 2 ) \bm v(t_2)v ( t2)は互いに独立しており、いつでもノイズを個別に分析できます。
    • 共分散行列は対角行列であり、各対角要素はv \bm vvの対応する要素の分散値
    • 単一の四足歩行ロボットのノイズの各項は通常、互いに独立していません。

4.5. 条件付き確率

  • 確率変数x \bm xの場合xと確率変数y \bm yy間で独立していないy \bm yy値の下のx \bm xx期望 E ( x ) E(\bm x) E ( x )は異なります
    • 已人= y 1 \bm y=\bm y_1y=y1条件付きx \bm xx はE { x ∣ y 1 } E\{\bm x|\bm y_1\}として表現されることが期待されます。E { x ∣ y1}

5. 最小二乗推定

  • 入力ベクトルy \bm yを測定しますy にはノイズ ベクトルが含まれている必要がありますv \bm vv、设xk \bm x_kバツｋ価値
    • yk = C x + vk \bm y_k=\bm C\bm x+\bm v_kyｋ=C ×+vｋ, v 〜 ( 0 , R ) \bm v\sim(0,\bm R)v〜( 0 ,R ),R = E ( vv T ) \bm R=E(\bm v\bm v^{\rm T})R=E ( v vT )対角行列

5.1. 加重最小二乗推定

  • 変数y = y − C x ^ \bm \epsilon_y=y-\bm C\hat{\bm x}ϵはい=y−Cバツ^
    • 各項目の二次和が最小値となったとき、状態ベクトルの値が最も推定される値x ^ \hat{\bm x}バツ^
    • J = ϵ y 1 2 + ϵ y 2 2 +とします。. . . . . . . . + ϵ yn 2 = ϵ y T ϵ y J=\epsilon_{y1}^2+\epsilon_{y2}^2+...+\epsilon_{yn}^2={\bm \epsilon}_{y} ^{\rm T}{\bm\epsilon}_{y}J=ϵy1 _2+ϵy2 _2+...+ϵn _2=ϵyTϵはい
    • 無限小、単数無限小J = ϵ y 1 2 σ 1 2 + ϵ y 2 2 σ 1 2 + 。. . . . . . . . + ϵ yn 2 σ 1 2 = ϵ y TRT ϵ y = ( y − C x ^ ) TR − 1 ( y − C x ^ ) = y TR − 1 y − y TR − 1 C x ^ − x ^ TCTR − 1 y − x ^ TCTR − 1 C x ^ \begin{行列} J=\frac{\epsilon_{y1}^2}{\sigma_1^2}+\frac{\epsilon_{y2}^2}{\sigma_1 ^2}+...+\frac{\epsilon_{yn}^2}{\sigma_1^2}={\bm \epsilon}_{y}^{\rm T}{\bm R^{\rm T}}{\bm \epsilon}_{y} \\ =(\bm y-\bm C\hat{\bm x})^{\rm T}{\bm R}^{-1}(\ bm y-\bm C\hat{\bm x}) \\= {\bm y^{\rm T}\bm R^{-1}\bm y} - {\bm y^{\rm T} \bm R^{-1}\bm C\hat{\bm x}} - {\hat{\bm x}^{\rm T}\bm C^{\rm T}\bm R^{-1 }\bm y} - {\hat{\bm x}^{\rm T}\bm C^{\rm T}\bm R^{-1}\bm C\hat{\bm x}} \end {マトリックス}J=p12ϵy1 _2​+p12ϵy2 _2​+...+p12ϵn _2​=ϵyTRTϵ _はい=( y−Cバツ^ )T R− 1 (y−Cバツ^ )=yT R− 1年−yT R− 1 ℃バツ^−バツ^TC _T R− 1年−バツ^TC _T R− 1 ℃バツ^
    • 行列R \bm R\;Rは対角行列R − 1 \bm R^{-1}R− 1は対角行列、各項目はR \bm RR対応導関数
    • 二次計画法で計算されるコスト関数の偏導関数は、 0 ∂ J ∂ x ^ = − 2 y TR − 1 C + 2 x ^ TCTR − 1 C = 0 \frac{\partial J}{\partial\hat {\bm x}}=-2{\bm y^{\rm T}\bm R^{-1}\bm C}+{2\hat{\bm x}^{\rm T}\bm C ^{\ rm T}\bm R^{-1}\bm C}=0∂バツ^∂ J=−2年_T R− 1 ℃+2バツ^TC _T R− 1 ℃=0
      • 正しい状態を取得x \bm xxの最適推定結果x ^ = ( CTR − 1 C ) − 1 CTR − 1 y \hat{\bm x}=(\bm C^{\rm T}\bm R^{-1}\bm C )^{-1}\bm C^{\rm T}\bm R^{-1}\bm yバツ^=( CT R−1 ℃） _− 1 ℃T R− 1年

5.2. 再帰的最小二乗推定

  • 上記の最適な推定結果を得るには、一定期間のすべての測定値を使用する必要がありますy の場合、行列は非常に大きくなり、占有メモリが速度に影響するため、再帰的最小二乗推定が使用されます。
  • 状態x \bm xx x ^ \hat{\bm x}の最良推定値バツ^递推公式{ yk = C x + vkx ^ k = x ^ k − 1 + K k ( yk − C x ^ k − 1 ) \left\{ \begin{行列} {\bm y}_k={\ bm C\bm x}+{\bm v}_k\\ \hat{\bm x}_k=\hat{\bm x}_{k-1}+{\bm K}_k(\bm y_k-\ bm C\hat{\bm x}_{k-1})\end{行列} \right。{ yｋ=C ×+vｋバツ^ｋ=バツ^k − 1+Kｋ( yｋ−Cバツ^k − 1)
    • yk \bm y_kyｋ: 状態ベクトルx \bm xを仮定した、現時点での測定結果xは固定定数です
    • vk \bm v_kvｋ: 現時点のノイズベクトル
    • x ^ k − 1 \hat{\bm x}_{k-1}バツ^k − 1: K k ( yk − C x ^ k − 1 ) {\bm K_k}(\bm y_k-\bm C\hat{\bm x}_{k-1}) による最後の瞬間の最適な状態推定値Kｋ( yｋ−Cバツ^k − 1)を修正して、現在の最適な状態推定値x ^ k \hat{\bm x}_kバツ^ｋ
    • K k \bm K_kKｋ: 最適な補正係数行列を求めるには、最適な補正係数行列を解く必要があります。
  • 最適な補正係数行列K k \bm K_kを解くKｋ
    • ｋｋ時刻kにおける状態推定誤差ω k = x − xk ^ = ⋯ = ( I − K k C ) ω k − 1 − K kvk {\bm\omega_k={\bm x}-\hat{\bm x_k} = \dots = (\bm I - \bm K_k\bm C){\bm \omega}_{k-1}-{\bm K}_k{\bm v}_k}おおｋ=バツ−バツｋ^=⋯=(私−KｋC ) ok − 1−Kｋvｋ
    • 二次計画法を使用して、kkとします。時間kにおける各状態推定の誤差分散の合計が最小になります。
      • コスト関数J k = E ( ω k 1 2 + ω k 2 2 + ⋯ + ω kn 2 ) = σ k 1 2 + σ k 2 2 + ⋯ + σ kn 2 = T r ( P k ) \begin{matrix } J_k=E(\omega_{k1}^2+\omega_{k2}^2+\dots+\omega_{kn}^2)\\=\sigma_{k1}^2+\sigma_{k2}^2+ \dots+\sigma_{kn}^2\\=\rm Tr(\bm P_k)\end{行列}Jｋ=E (ああk1 _2+おおk2_ _2+⋯+おお知っている2)=pk1 _2+pk2_ _2+⋯+p知っている2=Tr ( Pｋ)
        • P k = E ( ω k ω k T ) \bm P_k=E(\bm\omega_k\bm\omega_k^{\rm T})Pｋ=E (ああｋおおkT) :ωk\bm\omega_kおおｋKで時間kでの共分散行列は対称行列であり、対角要素は各誤差の分散、つまりJ k J_kJｋT r ( P k ) \rm Tr(\bm P_k)として表すことができます。Tr ( Pｋ)
        • 状態推定誤差ω k − 1 \bm\omega_{k-1} を展開して考察します。おおk − 1および測定ノイズvk − 1 \bm v_{k-1}vk − 1は互いに独立しており、平均ノイズがゼロであるため、共分散漸化式 P k = ( I − K k C ) P k − 1 ( I − K k C ) T + K k RK k T \bm P_k= ( \bm I-\bm K_k\bm C)\bm P_{k-1}(\bm I-\bm K_k\bm C)^{\rm T}+{\bm K}_k{\bm R} { \bm K}_{k}^{\rm T}Pｋ=(私−KｋC ) Pk − 1(私−KｋC )T+KｋR KkT
          • R \bm RR : 測定誤差v \bm vvの共分散kk)時間kにおける推定誤差共分散P k \bm P_kPｋ前の瞬間との共分散P k − 1 \bm P_{k-1}Pk − 1と測定誤差の共分散R \bm RR関連
      • 偏求: ∂ J k ∂ K k = ∂ T r ( P k ) ∂ K k = 0 \frac{\partial J_k}{\partial\bm K_k}=\frac{\partial{\rm Tr} (\bm P_k)}{\partial\bm K_k}=0∂K _ｋ∂ Jｋ​=∂K _ｋ∂ Tr ( Pｋ)=0
      • 得られる最有利K k = P k − 1 CT ( R + CP k − 1 CT ) − 1 \bm K_k={\bm P_{k-1}\bm C^{\rm T}(\bm R+\bm C\bm P_{k-1}\bm C^{\rm T})^{-1}}Kｋ=Pk − 1CT (R+CP _k − 1Cた）− 1
  • 最小二乗推定の計算過程
  • 初期ドリルパイプの最適すぎる推定値を決定しますx ^ 0 \hat{\bm x}_0バツ^0推定値P 0 \bm P_0との共分散P0
    • システム状態x \bm xのときx はまったく理解できません。x0 ^ \hat{\bm x_0}バツ0^任意の値に設定します。P 0 = ∞ I \bm P_0=\infty \bm IP0=∞私(自信が非常に低い)
    • x 0の場合^ \hat{\bm x_0}バツ0^確かに、P 0 = 0 \bm P_0=0とします。P0=0
  • 実行開始時間k = 1 k=1k=1、時間kkk時間
    • K k = P k − 1 CT ( R + CP k − 1 CT ) − 1 x ^ k = x ^ k − 1 + K k ( yk − C x ^ k − 1 ) P k = ( I − K k C ) P k − 1 ( I − K k C ) T + K k RK k T \begin{行列} {\bm K}_k={\bm P}_{k-1}{\bm C}^{\ rm T}(\bm R+{\bm C}{\bm P}_{k-1}{\bm C}^{\rm T})^{-1} \\ \hat{\bm x}_k =\hat{\bm x}_{k-1}+{\bm K}_k(\bm y_k-{\bm C}\hat{x}_{k-1}) \\ {\bm P} _k=(\bm I-\bm K_k\bm C){\bm P}_{k-1}(\bm I-\bm K_k\bm C)^{\rm T}+{\bm K}_k {\bm R}{\bm K}_k^{\rm T} \end{行列}Kｋ=Pk − 1CT (R+CP _k − 1Cた）− 1バツ^ｋ=バツ^k − 1+Kｋ( yｋ−Cバツ^k − 1)Pｋ=(私−KｋC ) Pk − 1(私−KｋC )T+KｋR KkT​
  • k = 2 、 3 、 . 。。k=2,3,...k=2 、3 、...推定器がステップを繰り返すと、推定値x ^ k \hat{\bm x}_kバツ^ｋ現実の状態に近づき続けますx \bm xバツ

5.3. 状態ベクトルと共分散の時間の経過に伴う変化

  • 離散状態空間モデルへのプロセス ノイズwwの追加w :xk = A xk − 1 + B uk − 1 + wk − 1 {\bm x}_k={\bm A\bm x}_{k-1}+{\bm B\bm u}_{k -1}+{\bm w}_{k-1}バツｋ=あ×k − 1+ぶう_k − 1+wk − 1
    • プロセス ノイズはゼロであると予想されます。P k = E ( ω k ω k T ) = [ ( xk − xk ‾ ) ( xk − xk ‾ ) T ] = A x ‾ k − 1 + B uk − 1 {\ bm P_k} =E(\bm \omega_k\bm\omega_k^{\rm T})=[(\bm x_k-\overline{\bm x_k})(\bm x_k-\overline{\bm x_k})^ {\rm T}]={\bm A}\overline{\bm x}_{k-1}+{\bm B}{\bm u}_{k-1}Pｋ=E (ああｋおおkT)=[( xｋ−バツｋ​) ( ×ｋ−バツｋ​)た]=あバツk − 1+ぶう_k − 1
  • P k = AP k − 1 AT + Q \bm P_k=\bm A\bm P_{k-1}\bm A^{\rm T}+\bm QPｋ=ＡＰ_k − 1あT+Q
    • 今の瞬間、kk状態ベクトルの共分散P k \bm P_kPｋそしてP k − 1 \bm P_{k-1}Pk − 1とプロセスノイズの共分散Q \bm QQ関連。
      • Q \bm QQはシステムにのみ関係し、時間には関係しません

6. 離散カルマンフィルター

  • 既知のホワイト ノイズ共分散行列QR \bm Q\bm RQ Rと各瞬間の測定値の条件y \bm yy、現在の k 時点でのシステムの最適な状態ベクトルを推定します。
    • { xk = A xk − 1 + B uk − 1 + wk − 1 yk = C xk + vk \left\{\begin{行列} {\bm x}_k={\bm A}{\bm x}_{ k-1}+{\bm B}{\bm u}_{k-1}+{\bm w}_{k-1} \\ {\bm y}_k={\bm C\bm x} _k+{\bm v}_k \end{行列}\right。{ バツｋ=あ×k − 1+ぶう_k − 1+wk − 1yｋ=C ×ｋ+vｋ​
      • プロセスノイズw \bm wwと測定ノイズv \bm vvはすべてゼロ平均の無相関ホワイト ノイズです。w 〜 ( 0 , Q ) 、 v 〜 ( 0 , R ) {\bm w}\sim(0,\bm Q), {\bm v}\sim(0 , R)w〜( 0 ,問）、v〜( 0 ,R )
  • 事前推定値x ^ k − \hat{\bm x}_{k}^{-}バツ^k−: 1 のみを使用 → ( k − 1 ) 1\rightarrow(k-1)1→( k−1 )測定値y \bm yy はxk \bm x_kを推定しますバツｋ
    • x ^ k − = E { xk ∣ y 1 , y 2 , … , yk − 1 } \hat{\bm x}_{k}^{-}=E\{\bm x_k | \bm y_1,\bm y_2,\dots,\bm y_{k-1}\}バツ^k−=E { xｋ∣ y1、y2、…、yk − 1}
    • 事前共分散P k − = E [ ( xk − x ^ k − ) ( xk − x ^ k − ) ] \bm P_k^{-}=E[({\bm x}_k-\hat{\bm x} _k^{-})(\bm x_k-\hat{\bm x}_k^{-})]Pk−=そして[( xｋ−バツ^k−) ( ×ｋ−バツ^k−)]
  • 事後推定値x ^ k + \hat{\bm x}_{k}^{+}バツ^k+: 用1 → ( k ) 1\rightarrow(k)1→( k )測定値y \bm yy はxk \bm x_kを推定しますバツｋ
    • x ^ k + = E { xk ∣ y 1 , y 2 , … , yk − 1 , yk } \hat{\bm x}_{k}^{+}=E\{\bm x_k | \bm y_1,\bm y_2,\dots,\bm y_{k-1},\bm y_{k}\}バツ^k+=E { xｋ∣ y1、y2、…、yk − 1、yｋ}
    • 事後共分散P k + = E [ ( xk − x ^ k + ) ( xk − x ^ k + ) ] \bm P_k^{+}=E[({\bm x}_k-\hat{\bm x} _k^{+})(\bm x_k-\hat{\bm x}_k^{+})]Pk+=そして[( xｋ−バツ^k+) ( ×ｋ−バツ^k+)]

より多くの測定値が使用されるほど、推定精度は高くなります。事後推定は事前推定よりも状態ベクトルの真の値に近くなります。事後共分散 < ​​事前共分散

  • カルマンフィルター
    • x ^ k − 1 + \hat{\bm x}_{k-1}^{+}よりバツ^k − 1+x ^ k − \hat{\bm x}_{k}^{-}にバツ^k−、時間的に 1 ステップ進みますが、新しい観測はありません。すべて1 → ( k − 1 ) 1\rightarrow(k-1)1→( k−1 )所見
      • { x ^ k − = A x ^ k − 1 + + B uk − 1 P k − = AP k − 1 + AT + Q \left\{\begin{行列} \hat{\bm x}_k^-= \bm A\hat{\bm x}_{k-1}^++{\bm B}{\bm u}_{k-1} \\ {\bm P}_k^-={\bm A }{\bm P}_{k-1}^+{\bm A}^{\rm T}+{\bm Q} \end{行列}\right。{ バツ^k−=あバツ^k − 1++ぶう_k − 1Pk−=ＡＰ_k − 1+あT+Q前の瞬間から前の現在の瞬間を計算します。
    • 新しい観測値が取得された後、事後現在時刻を計算できます。
      • { K k = P k − CT ( R + CP k − CT ) − 1 x ^ k + = x ^ k − + K k ( yk − C x ^ k − ) P k + = ( I − K k C ) P k − ( I − K k C ) T + K k RK k T \left\{\begin{行列} {\bm K}_k={\bm P}_{k}^{-}{\bm C }^{\rm T}(\bm R+{\bm C}{\bm P}_{k}^{-}{\bm C}^{\rm T})^{-1} \\ \hat {\bm x}_k^{+}=\hat{\bm x}_{k}^{-}+{\bm K}_k(\bm y_k-{\bm C}\hat{x}_{ k}^{-}) \\ {\bm P}_k^{+}=(\bm I-\bm K_k\bm C){\bm P}_{k}^{-}(\bm I- \bm K_k\bm C)^{\rm T}+{\bm K}_k{\bm R}{\bm K}_k^{\rm T} \end{行列}\right。⎩ ⎨ ⎧Kｋ=Pk−CT (R+CP _k−Cた）− 1バツ^k+=バツ^k−+Kｋ( yｋ−Cバツ^k−)Pk+=(私−KｋC ) Pk−(私−KｋC )T+KｋR KkT​
        • K k \bm K_kKｋ: カルマン フィルター ゲイン、xk + ^ \hat{\bm x_k^+}バツk+^: 事後推定値は、時刻 k における最適な推定値です。

離散カルマンフィルター計算処理

最小二乗推定に似ています

  • まず初期状態の最適状態推定値x ^ 0 + \hat{\bm x}_0^+ を与えます。バツ^0+共分散ありP 0 + \bm P_0^+P0+（信憑性により判断します）
  • 時間 k=1 まで実行を開始し、最初に事前推定値と事前分散を計算します。
    • { x ^ k − = A x ^ k − 1 + + B uk − 1 P k − = AP k − 1 + AT + Q \left\{\begin{行列} \hat{\bm x}_k^-= \bm A\hat{\bm x}_{k-1}^++{\bm B}{\bm u}_{k-1} \\ {\bm P}_k^-={\bm A }{\bm P}_{k-1}^+{\bm A}^{\rm T}+{\bm Q} \end{行列}\right。{ バツ^k−=あバツ^k − 1++ぶう_k − 1Pk−=ＡＰ_k − 1+あT+Q
  • カルマンフィルターゲインの計算
    • K k = P k − CT ( R + CP k − CT ) − 1 {\bm K}_k={\bm P}_{k}^{-}{\bm C}^{\rm T}(\ bm R+{\bm C}{\bm P}_{k}^{-}{\bm C}^{\rm T})^{-1}Kｋ=Pk−CT (R+CP _k−Cた）− 1
  • 各センサーの測定値を読み取り、行列に取り込んでyk \bm y_kを取得します。yｋ、事後推定値と事後共分散を計算する場合
    • { x ^ k + = x ^ k − + K k ( yk − C x ^ k − ) P k + = ( I − K k C ) P k − ( I − K k C ) T + K k RK k T \left\{\begin{行列} \hat{\bm x}_k^{+}=\hat{\bm x}_{k}^{-}+{\bm K}_k(\bm y_k-{ \bm C}\hat{x}_{k}^{-}) \\ {\bm P}_k^{+}=(\bm I-\bm K_k\bm C){\bm P}_{ k}^{-}(\bm I-\bm K_k\bm C)^{\rm T}+{\bm K}_k{\bm R}{\bm K}_k^{\rm T} \end {マトリックス}\そうです。{ バツ^k+=バツ^k−+Kｋ( yｋ−Cバツ^k−)Pk+=(私−KｋC ) Pk−(私−KｋC )T+KｋR KkT​
  • k = 2 , 3 , … k=2,3,\dotsk=2 、3 、...ステップを繰り返します

7. 共分散の測定

  • 離散カルマン フィルターで決定される: プロセス ノイズ共分散Q \bm QQ、測定ノイズ共分散R \bm RR (各読み取り測定値の共分散、決定が容易)
    • 多数の測定値を保存したい場合、メモリが十分ではないため、平均と共分散を段階的に再帰的に計算する方法が必要です

7.1. 平均値と共分散の漸化式

  • 均值x ‾ n = x ‾ n − 1 + xn − x ‾ n − 1 n \overline{\bm x}_n=\overline{\bm x}_{n-1}+\frac{ {\bm x } _n-\overline{\bm x}_{n-1}}{n}バツん=バツn − 1+nバツん−バツn − 1​
  • 协方差C n = n − 1 n 2 ( xn − x ‾ n − 1 ) ( xn − x ‾ n − 1 ) T + n − 1 n C n {\bm C_n}=\frac{n-1}{ n^2}({\bm x}_n-\overline{\bm x}_{n-1})({\bm x}_n-\overline{\bm x}_{n-1})^{ \rm T}+\frac{n-1}{n}{\bm C}_nCん=n2n − 1( ×ん−バツn − 1) ( ×ん−バツn − 1)T+nn − 1Cん

7.2. 四足センサーの共分散の測定

  • 静止時の測定ノイズv \bm vv共分散R \bm RR = 測定値y \bm yyの共分散 C= 1 n ∑ k = 1 nvkvk T = R \bm C_y=\frac{1}{n}\sum_{k=1}^n{\bm v_k}{\bm v}_k^ {\ rm T}={\bm R}Cはい=n1∑k = 1んvｋvkT=R
  • R \bm Rを取得する再帰的メソッドR和C u \bm C_uCあなた
  • プロセスノイズの共分散Q \bm QQ には入力ボリュームノイズ共分散C u \bm C_uCあなた、入力ノイズのみを考慮
    • xk = A xk − 1 + B uk − 1 + wk − 1 = A xk − 1 + B ( uk − 1 + ok − 1 ) = A xk − 1 + B uk − 1 + B ok − 1 \begin{行列} {\bm x}_k={\bm A}{\bm x}_{k-1}+{\bm B}{\bm u}_{k-1}+{\bm w}_{k -1} \\ ={\bm A}{\bm x}_{k-1}+{\bm B}({\bm u}_{k-1}+{\bm o}_{k- 1}) \\ ={\bm A}{\bm x}_{k-1}+{\bm B}{\bm u}_{k-1}+{\bm B}{\bm o} _{k-1} \end{行列}バツｋ=あ×k − 1+ぶう_k − 1+wk − 1=あ×k − 1+B ( uk − 1+ああk − 1)=あ×k − 1+ぶう_k − 1+ボ_k − 1​
    • Q u = BC u BT \bm Q_u={\bm B}{\bm C_u}{\bm B}^{\rm T}Qあなた=BC _あなたBT

8. 離散カルマンフィルターの調整

8.1. 共分散

  1. プロセスノイズ共分散QQが与えられた場合Q、測定ノイズ共分散RRR、初期最適推定共分散P 0 + P_0^+P0+同じ係数 a を乗算しても、離散ケルマン フィルターの計算結果は変わりません。
    1. 共分散行列は、計算に便利な大きさのオーダーで任意にスケーリングできます。
  2. 離散カルマン フィルターには状態空間モデルが含まれており、これは、独自の状態空間モデルによって推定された状態と、重み Q、R による測定値によって推定された状態の間の「重み付き最小二乗推定」と考えることができます。
    1. Q↓: 状態空間モデルは信頼しないでください。精度が悪いと結果が間違ってしまいます。
    2. Q↑: R↓、測定値を過度に信頼し、測定ノイズが大きい場合、推定にも大きなノイズが発生し、状態ベクトルに高周波振動が発生します。
    3. デバッグ Q: 推定結果に大きな誤差が生じないように、最初は大きな Q を与え、高周波の振動が発生する場合は徐々に Q を下げます。

8.2. 空中とタッチダウン

  1. 状態空間モデルの足端の位置は、飛行中の足端が地面に接触していることを基準とし、 Q → ∞ Q\rightarrow \inftyQ→∞、QQがQ
  2. 可变协方差: 分段関数: σ ( x ) { xwrx < wr 1 wr ≤ x ≤ 1 − wr 1 − xwrx > 1 − wr \sigma (x)\left\{\begin{matrix} \frac{x }{w_r} & x<w_r\\ 1 & w_r\le x\le 1-w_r\\ \frac{1-x}{w_r} & x>1-w_r\end{matrix}\right。σ ( x )⎩ ⎨ ⎧wr×1wr1 − ×​バツ<wrwr≤バツ≤1−wrバツ>1−wr​
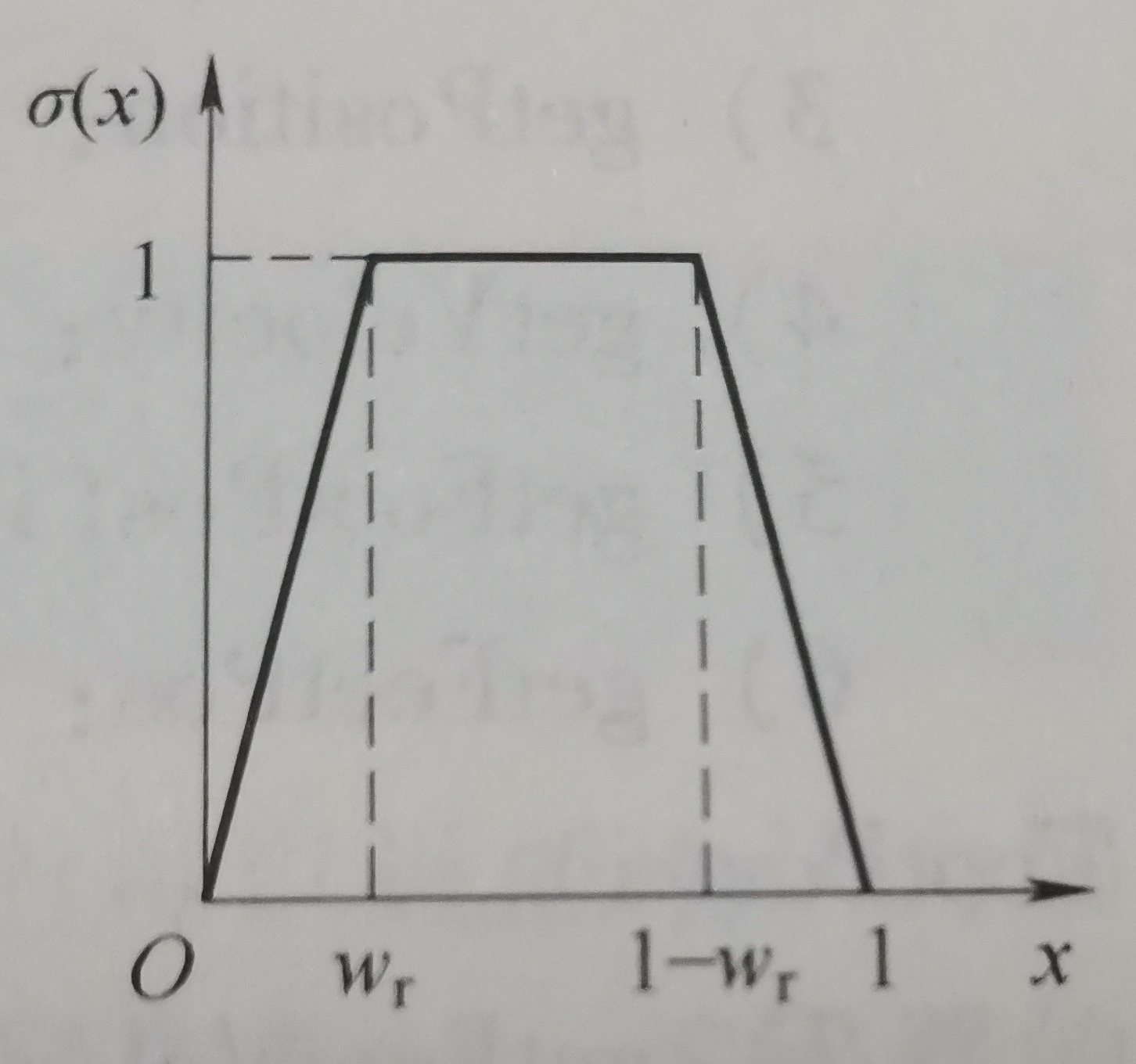
    1. ここに画像の説明を挿入
    2. C スタンス = [ 1 + ( 1 − σ ) L ] C init C_{スタンス}=[1+(1-\sigma)L]C_{init}Cとりあえず_ _ _=[ 1+( 1−s ) L ] C初期化、C init C_{init}C初期化定常タッチダウン時のノイズ共分散行列
  3. 飛行時の位置は順運動学によって計算されます

参照

<四足ロボットの制御アルゴリズム - モデリング、制御、実践>

おすすめ

転載: blog.csdn.net/weixin_46143152/article/details/131343205
おすすめ
オープンソース 1 周年、清語の新バージョンがリリース
ランキング
[Linuxは] centos7接続が必要なIPアドレスのルックアップをxshell
分散システムのCAP理論
四つの基本的なコアSQL文（基礎）
オブザーバーモードの概要
【Uiautomatorviewer】报错：予期しないエラーUI階層java.lang.reflect.InvocationTを得ながら...
JavaのグラフィカルなデザインパターンVisitorパターン
ドライビングレンジのネットワークPATオフ牛 - いくつかのPATがあります
前端面からの質問：どのように配列にカスタムメソッドを追加します
ファイル比較（diff）、置換（sed）
迅速VUEを生成するために、VSCカスタムテンプレート
アーカイブ
もっと
2024-06-01(1)
2024-05-31(1)
2024-05-30(0)
2024-05-29(1)
2024-05-28(0)
2024-05-27(1)
2024-05-26(0)
2024-05-25(1)
2024-05-24(11)
2024-05-23(35)

コードワールド

© 2018 codetd.com