ロボット学習 - 古典的なパス計画について (1)

1. はじめに

• さまざまなタイプの経路計画アルゴリズムを特定する
• 一連のアルゴリズムの内部動作を理解する
• 特定のアプリケーションに対するアルゴリズムの適合性を評価する
• 検索アルゴリズムを実装する

2. 経路計画の例

用語

完全性- アルゴリズムは、開始点と目標の間のパスを見つけることができれば完成します。

最適性- 最適なソリューションを見つけることができれば、アルゴリズムは最適です。

バグアルゴリズム

次の問題は、解決策はあるものの、バグ アルゴリズムが解決策を見つけられない例を示しています。

ロボットは障害物の外壁の周囲を無限に移動しますが、バグ アルゴリズムのいくつかのバリアントでこのエラーを補うことができます。ほとんどの経路計画アルゴリズムは、この記事で紹介する他の原則に依存しています。新しいアルゴリズムを研究する場合、アルゴリズムのタスクへの適用可能性を分析する際に、完全性と最適性の概念を再考します。

3. パス計画方法
パス計画方法
この記事では、3 つの異なるパス計画方法を検討します。1 つ目は、離散 (または組み合わせ) パス プランニングと呼ばれ、3 つの方法の中で最も簡単です。サンプルベースのパス プランニングと確率的パス プランニングと呼ばれる他の 2 つのアプローチは、より広範囲に適用可能なパス プランニング ソリューションを開発するための離散プログラミングに基づいています。

離散プログラミング
離散プログラミングは、ロボットのワークスペースを接続されたグラフに明示的に離散化し、グラフ探索 (グラフ探索) アルゴリズムを適用して最適なパスを計算します。このプロセスは非常に正確で (実際、精度は空間の離散化の細かさを変更することで明示的に調整できます)、ワークスペース全体を離散化するため、非常に徹底的です。その結果、離散プログラミングは計算コストが非常に高くなる可能性があり、大規模なパス計画の問題には法外なコストがかかる可能性があります。
以下の図は、2D ワークスペースに適用される離散パス プランニングの可能な実装の 1 つを示しています。

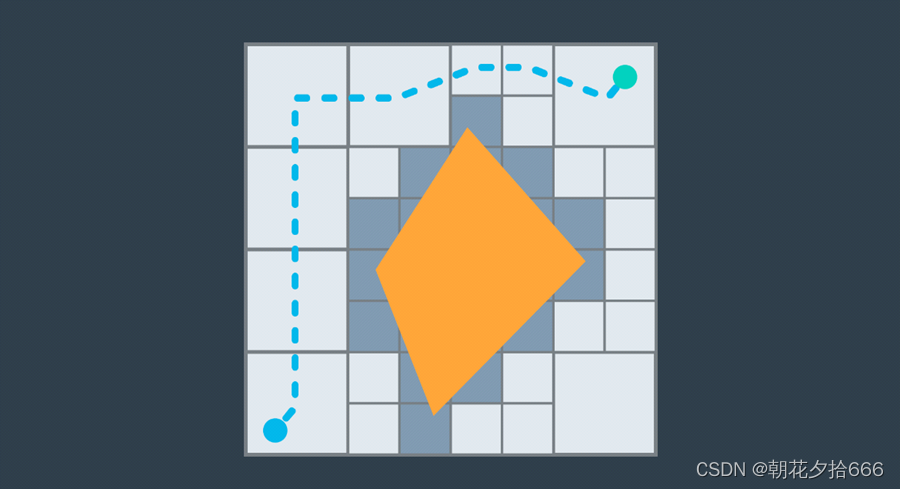
離散パス計画は精度が優れていますが、低次元の問題に最適です。高次元の問題の場合は、サンプルベースのパス計画の方がより適切なアプローチです。
サンプルベースの計画

サンプルベースのパス プランニングでは、ワークスペースを調査して段階的にグラフを構築します。離散ワークスペースの各部分とは異なり、サンプルベースの計画では多くのサンプルを取得し、それらを使用してワークスペースの離散表現を構築します。結果として得られるグラフは、離散プログラミングを使用して作成されたグラフほど正確ではありませんが、使用されるサンプルの数が比較的少ないため、構築がはるかに速くなります。
サンプルベースの計画を使用して生成されたパスは最適ではない可能性がありますが、アプリケーションによっては、最適なパスを生成するために数時間、場合によっては数日待つよりも、実現可能なパスを迅速に生成する方が良い場合があります。

以下の図は、サンプルベースの計画を使用して作成された 2D ワークスペースのグラフィック表現を示しています。

確率的パス プランニング
このモジュールで学習する最後のタイプのパス プランニングは、確率的パス プランニングです。最初の 2 つのアプローチでは、誰が、または何がアクションを実行するかを知らずに、一般的に経路計画の問題を検討しますが、確率的経路計画では、ロボットの動作の不確実性が考慮されます。
これは一部の環境では大きなメリットが得られない場合がありますが、非常に制限された環境や、敏感なエリアやリスクの高いエリアがある環境では特に役立ちます。
以下の図は、危険を含む環境 (右上の湖) に適用された確率的経路計画を示しています。

マルチレッスン マップ
この記事では、いくつかの離散パス計画アルゴリズムとサンプルベースおよび確率計画を学習し、それをパス計画実験に適用し、C++ を使用して検索アルゴリズムを作成します。

4. 連続性表現
ロボットのジオメトリを考慮し、経路計画のタスクを簡素化するために、ワークスペース内の障害物を膨張させて、構成スペース (または C スペース) と呼ばれる新しいスペースを作成できます。障害物のエッジはロボットの半径に応じて拡大し、ロボット本体を点とみなすことができるため、アルゴリズムによる経路の探索が容易になります。C スペースはすべてのロボットのポーズのコレクションであり、C_Free と C_Obs に分解できます。

5. ミンコフスキー和
ミンコフスキー
和 ミンコフスキー和は、特定の障害物とロボットのジオメトリの構成空間を計算するために使用できる数学的特性です。
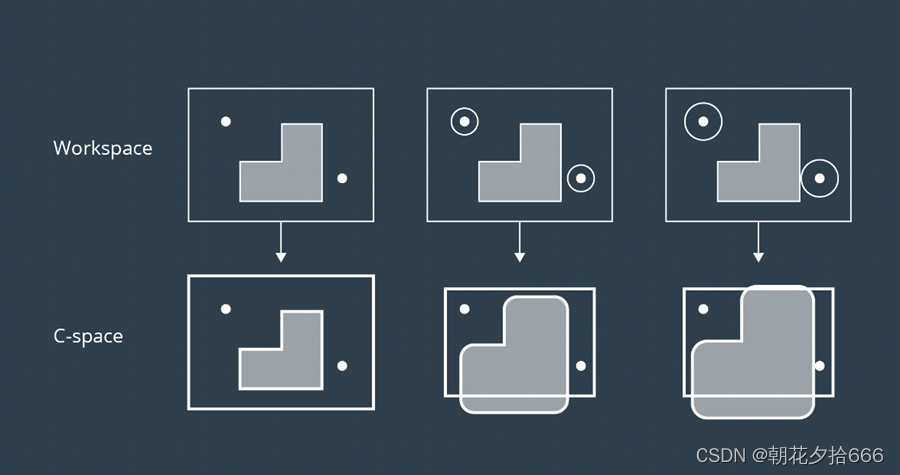
ミンコフスキーの和計算法の直観は、ロボットのような形状のブラシで障害物の外側をペイントすることを想像すると理解できます。ロボットの原点はブラシの先端です。ペイントされた領域は C_obs です。以下の図はこれを示しています。

構成空間を作成するには、ワークスペース内の障害物ごとにミンコフスキー和がこの方法で計算されます。下の画像は、サイズの異なる 3 台のロボットによって 1 つのワークスペースから作成された 3 つの構成スペースを示しています。ご覧のとおり、ロボットが単なる点である場合、ワークスペース内の障害物は C スペースを作成するためにわずかに膨張するだけです。ロボットのサイズが大きくなるにつれて、障害物もどんどん大きくなっていきます。

凸多角形の場合、畳み込みの計算は簡単で線形時間で実行できますが、非凸多角形 (ギャップや穴のある多角形) の場合、計算コストがはるかに高くなります。
ミンコフスキー和をさらに詳しく理解することに興味がある場合は、次のリソースを参照してください。

• ミンコフスキーの和と差に関するブログ投稿、

• ビデオ ゲームで衝突がどのように検出されるかについての興味深い読み物です。

クイズ: ミンコフスキー和

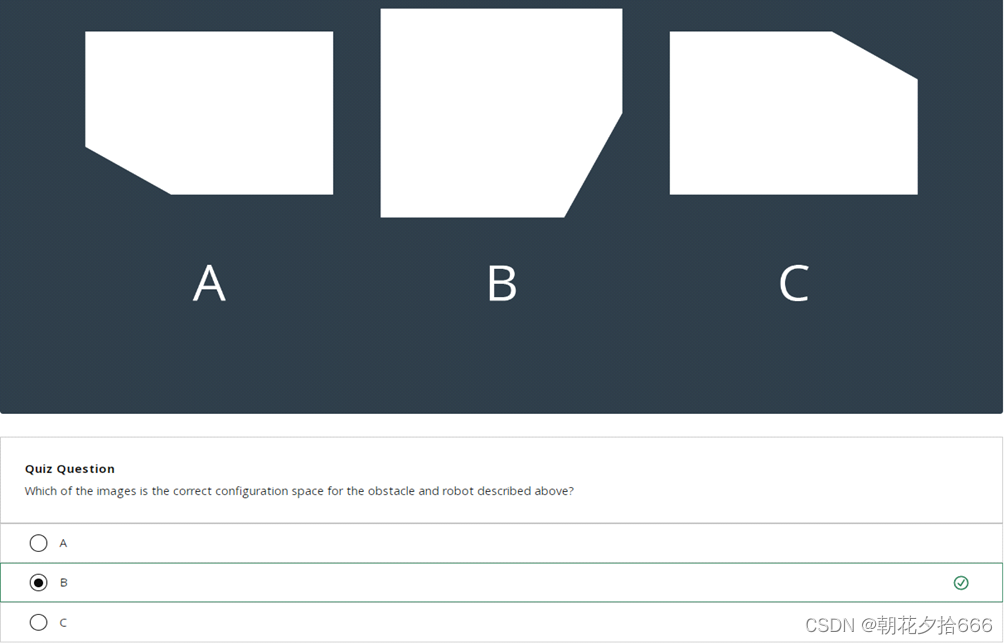
以下に示すように:

上に示したロボット (紫) と障害物 (白) の構成空間を表す画像は次のどれですか? 答え: B

6. ミンコフスキー総和の C++ 実装ミンコフスキー総和を
学習したので、C++ でコードを書いてみてください!図は次のとおりです。 

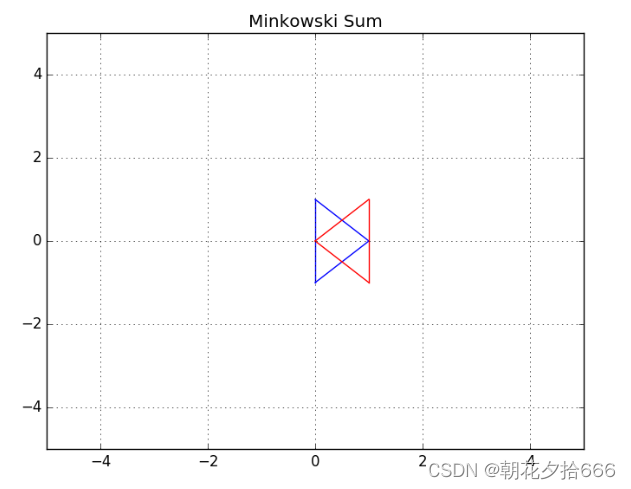
この例では、青と赤の 2 つの三角形が表示されます。ロボットが青い三角形で表され、障害物が赤い三角形で表されるとします。タスクは、ロボット A と障害物 B の構成空間 C を C++ で計算することです。

• ロボット:青い三角形、A で示す
• 障害物:赤い三角形、B で示されます。

 C++ でミンコフスキー和を記述する手順は次のとおりです。

   

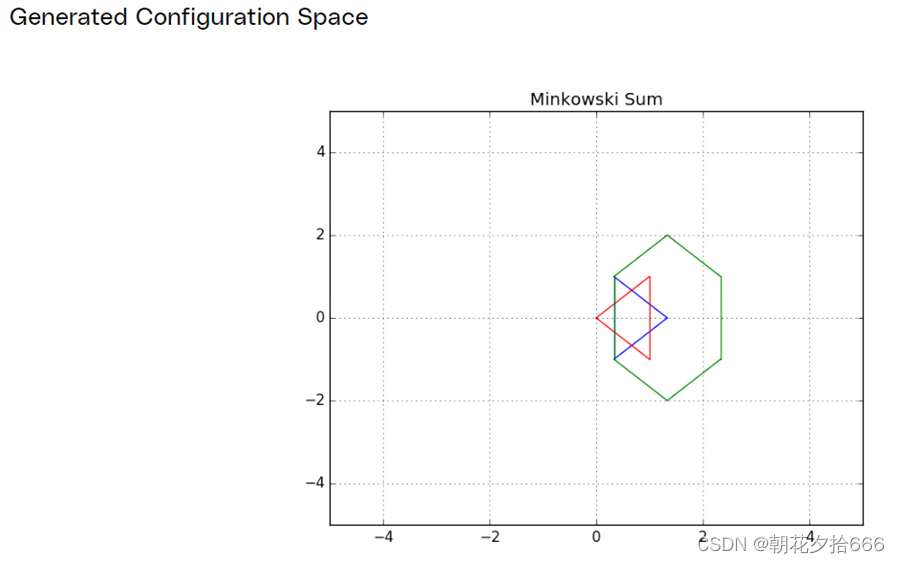
シフトされていない (変換されていない) 凡例
ミンコフスキー加算コードは上記で C++ で記述され、構成空間が生成されました。赤い障害物が完全に膨らんでいないことに注意してください。青いロボットはまだ障害物に当たる可能性があります。これは、構成空間を障害物に転送する必要があるためです。
まずロボットを障害物に変換し、配置空間を計算してロボットと障害物に変換します。
変換された凡例

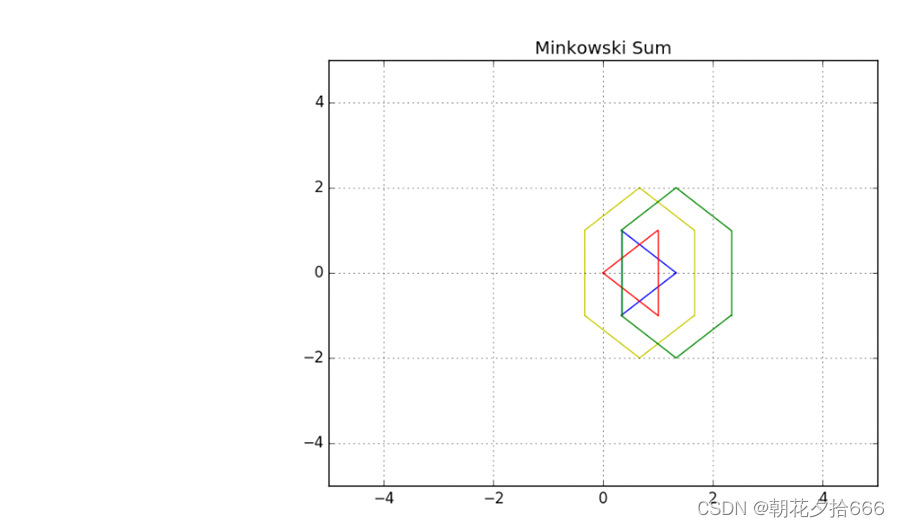
上の画像は変換後の最終画像で、青いロボットと緑の構成空間の両方が変換されています。黄色の塗りつぶしが表示されます。これは、赤い障害物に囲まれた、変換された構成空間を表しています。青いロボットはうまく膨らむため、赤い障害物にぶつかることはなくなります。

完全なコードは次のとおりです: (詳細については、https: //github.com/udacity/RoboND-MinkowskiSumを参照してください)。

#include <iostream>
#include <vector>
#include <algorithm>
#include "../lib/matplotlibcpp.h"
#include <math.h>

using namespace std;
namespace plt = matplotlibcpp;

// Print 2D vectors coordinate values
void print2DVector(vector<vector<double> > vec)
{
    for (int i = 0; i < vec.size(); ++i) {
        cout << "(";
        for (int j = 0; j < vec[0].size(); ++j) {
            if (vec[i][j] >= 0)
                cout << vec[i][j] << "  ";
            else
                cout << "\b" << vec[i][j] << "  ";
        }
        cout << "\b\b)" << endl;
    }
}

// Check for duplicate coordinates inside a 2D vector and delete them
vector<vector<double> > delete_duplicate(vector<vector<double> > C)
{
    // Sort the C vector
    sort(C.begin(), C.end());
    // Initialize a non duplicated vector
    vector<vector<double> > Cn;
    for (int i = 0; i < C.size() - 1; i++) {
        // Check if it's a duplicate coordinate
        if (C[i] != C[i + 1]) {
            Cn.push_back(C[i]);
        }
    }
    Cn.push_back(C[C.size() - 1]);
    return Cn;
}

// Compute the minkowski sum of two vectors
vector<vector<double> > minkowski_sum(vector<vector<double> > A, vector<vector<double> > B)
{
    vector<vector<double> > C;
    for (int i = 0; i < A.size(); i++) {
        for (int j = 0; j < B.size(); j++) {
            // Compute the current sum
            vector<double> Ci = { A[i][0] + B[j][0], A[i][1] + B[j][1] };
            // Push it to the C vector
            C.push_back(Ci);
        }
    }
    C = delete_duplicate(C);
    return C;
}

// Compute the centroid of a polygon
vector<double> compute_centroid(vector<vector<double> > vec)
{
    vector<double> centroid(2);
    double centroid_x=0, centroid_y=0;
    for (int i = 0; i < vec.size(); i++) {
        centroid_x += vec[i][0];
        centroid_y += vec[i][1];
    }
    centroid[0] = centroid_x / vec.size();
    centroid[1] = centroid_y / vec.size();
    return centroid;
}

// Compute the angle of each point with respect to the centroid and append in a new column
// Resulting vector[xi,yi,anglei]
vector<vector<double> > compute_angle(vector<vector<double> > vec)
{
    vector<double> centroid = compute_centroid(vec);
    double prec = 0.0001;
    for (int i = 0; i < vec.size(); i++) {
        double dy = vec[i][1] - centroid[1];
        double dx = vec[i][0] - centroid[0];
        // If the point is the centroid then delete it from the vector
        if (abs(dx) < prec && abs(dy) < prec) {
            vec.erase(vec.begin() + i);
        }
        else {
            // compute the centroid-point angle
            double theta = (atan2(dy, dx) * 180) / M_PI;
            // append it to the vector in a 3rd column
            vec[i].push_back(theta);
        }
    }
    return vec;
}

// Sort the vector in increasing angle (clockwise) for plotting
vector<vector<double> > sort_vector(vector<vector<double> > vec)
{
    vector<vector<double> > sorted_vec = compute_angle(vec);
    // Change the 0 angle to 90 degrees
    for (int i = 0; i < sorted_vec.size(); i++) {
        if (sorted_vec[i][2] == 0)
            sorted_vec[i][2] = 90.0;
    }
    // Sort with respect to the 3rd column(angles)
    sort(sorted_vec.begin(),
        sorted_vec.end(),
        [](const vector<double>& a, const vector<double>& b) {
            return a[2] < b[2];
        });
    return sorted_vec;
}

// Process the shapes and plot them
void plot(vector<vector<double> > vec, string color)
{
    // Sort the vector coordinates in clockwise
    vector<vector<double> > sorted_vec;
    sorted_vec = sort_vector(vec);
    // Add the first element to the end of the vector
    sorted_vec.push_back(sorted_vec[0]);
    // Loop through vector original size
    for (int i = 0; i < sorted_vec.size() - 1; i++) {
        // Connect coordinate point and plot the lines (x1,x2)(y1,y2)
        plt::plot({ sorted_vec[i][0], sorted_vec[i + 1][0] }, { sorted_vec[i][1], sorted_vec[i + 1][1] }, color);
    }
}

// Translate the configuration space toward the obstacle
vector<vector<double> > shift_space(vector<vector<double> > B, vector<vector<double> > C)
{
    // Compute the obstacle and space centroids
    vector<double> centroid_obstacle = compute_centroid(B);
    vector<double> centroid_space = compute_centroid(C);
    // Compute the translations deltas
    double dx = centroid_space[0] - centroid_obstacle[0];
    double dy = centroid_space[1] - centroid_obstacle[1];
    // Translate the space
    for (int i = 0; i < C.size(); i++) {
        C[i][0] = C[i][0] - dx;
        C[i][1] = C[i][1] - dy;
    }
    return C;
}

// Draw A, B and C shapes
void draw_shapes(vector<vector<double> > A, vector<vector<double> > B, vector<vector<double> > C)
{
    //Graph Format
    plt::title("Minkowski Sum");
    plt::xlim(-5, 5);
    plt::ylim(-5, 5);
    plt::grid(true);

    // Draw triangle A
    plot(A, "b-");

    // Draw triangle B
    plot(B, "r-");

    // Draw configuration space C
    // Trasnlate the C space
    vector<vector<double> > shifted_C = shift_space(B, C);
    plot(shifted_C, "y-");
    // Plot the original C shape
    plot(C, "g-");
    
    //Save the image and close the plot
    plt::save("../images/Minkowski_Sum.png");
    plt::clf();
}

int main()
{
    // Define the coordinates of triangle A and B in 2D vectors
    vector<vector<double> > A(3, vector<double>(2));
    // Robot A
    A = {
        { 0, -1 }, { 0, 1 }, { 1, 0 },
    };
    vector<vector<double> > B(3, vector<double>(2));
    // Obstacle B
    B = {
        { 0, 0 }, { 1, 1 }, { 1, -1 },
    };
    
    // Translating Robot toward the obstacle
    A=shift_space(B,A);
    
    // Compute the Minkowski Sum of triangle A and B
    vector<vector<double> > C;
    C = minkowski_sum(A, B);

    // Print the resulting vector
    print2DVector(C);

    // Draw all the shapes
    draw_shapes(A, B, C);
    
    return 0;
}

つまり、任意のポリゴンを生成するには、次の手順に従う必要があります。

1. 各ポリゴンの重心を計算します
2. X 軸に対する各点の重心の角度を計算します。
3. ポイントを角度ごとに昇順 (時計回り) に並べ替えます。
4. 連続する各点の間に線を引く

7. 三次元配置空間

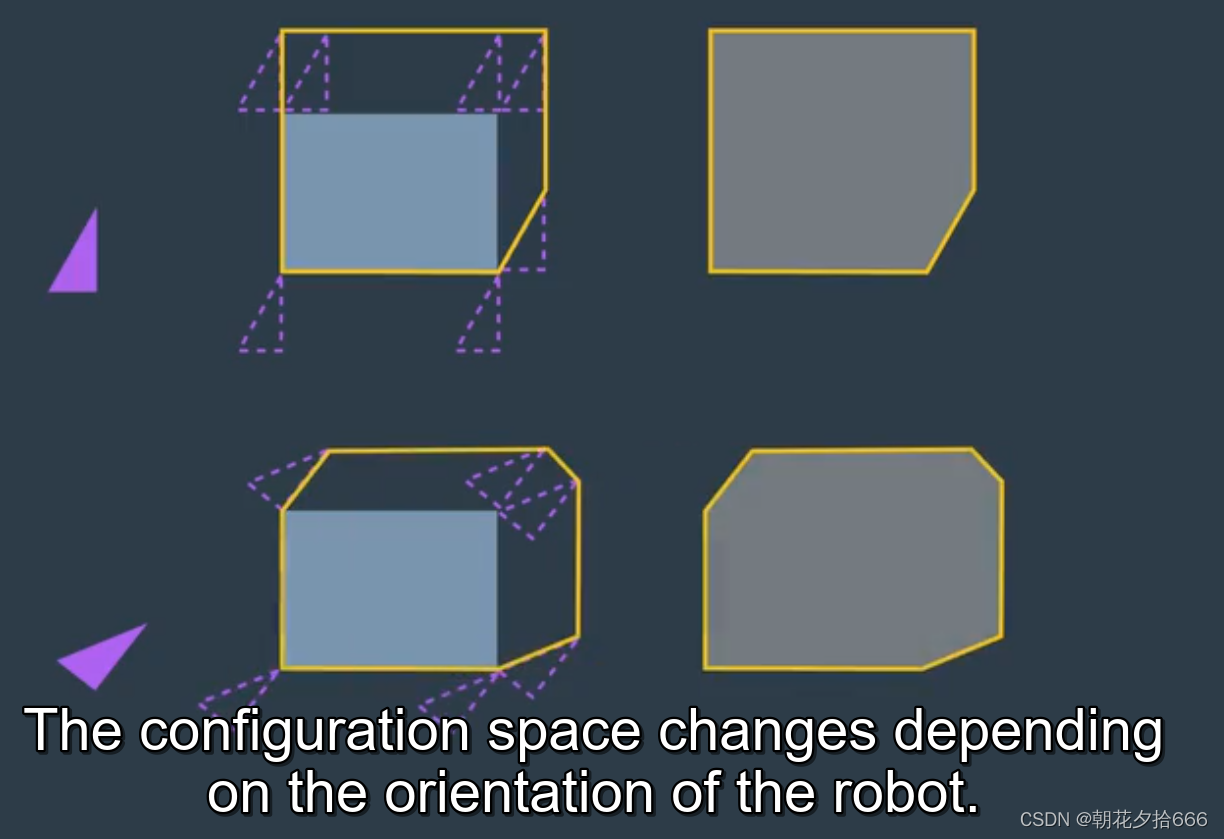
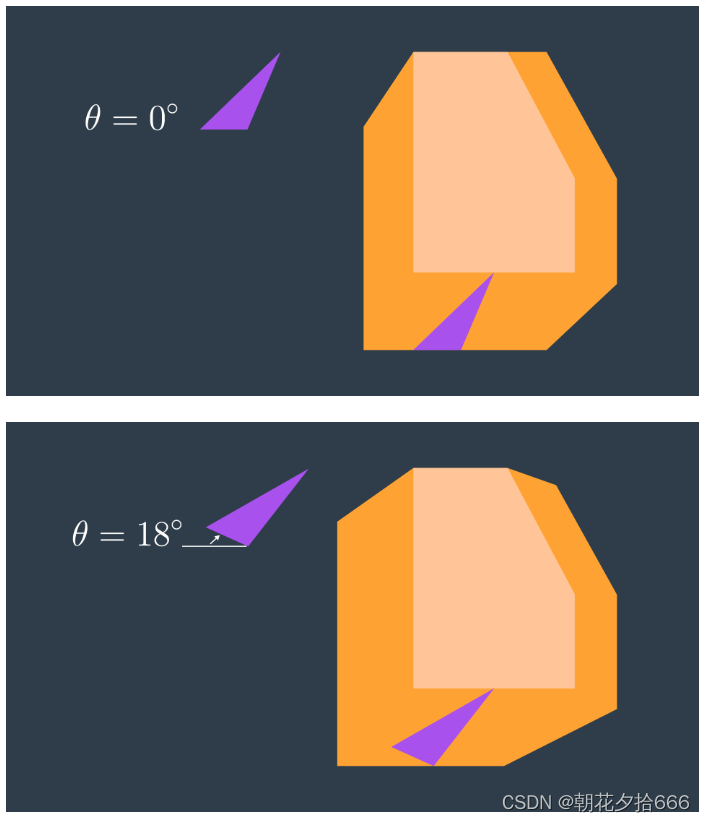
ロボットの構成空間はロボットの回転に依存しており、ロボットを回転させると自由度が増すため、構成空間も複雑になります。構成空間の次元は、ロボットが持つ自由度の数に等しくなります。2 次元の構成空間はロボットの x および y の平行移動を表現できますが、ロボットの回転を表現するには 3 次元が必要です。2 つの異なる回転に対するロボットとそれに対応する構成空間を見てみましょう。最初の角度は 0°、2 番目の角度は 18°です。

次の図に示すように、2 次元の構成空間をレイヤーに積み重ねることによって、3 次元の構成空間を生成できます。

ロボットの微小な回転の構成空間を計算し、それらを積み重ねると、次のようなグラフが得られます。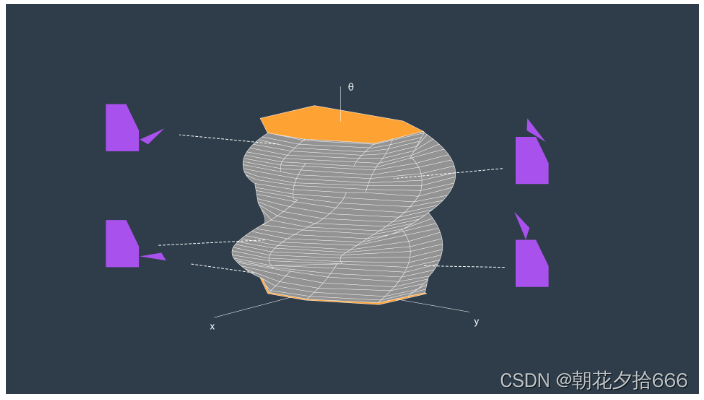 

上図は、2 次元での並進と Z 軸周りの回転が可能な三角形ロボットの配置空間を示しています。この画像は複雑に見えますが、3D 構成スペースを生成し、その周りを移動するために使用できるトリックがいくつかあります。次のビデオはベルリン自由大学によるもので、3D の構成空間を見事に視覚化したものです。このビデオでは、さまざまなタイプの動作を示し、特定のロボットの動作が 3D 構成空間にどのようにマッピングされるかを説明します:構成空間の視覚化 。