- 元のアドレス:Pythonで動的システムをシミュレートするための初心者向けガイド
- 原作者:Christian Hubbs
- 翻訳元:ナゲッツ翻訳プロジェクト
- この記事へのパーマリンク:github.com/xitu/gold-m…
- 翻訳者:Johnie Xu、Wang Ning
- 校正者:PorridgeZero、DylanXie123
Pythonを使用した2次常微分方程式の数値積分
そのような振り子モデルを考えてみましょう。

長さLのロープから質量mの重りが吊り下げられ、ロープが前後に揺れます。
これは基本的に私たちが手に入れることができる最も単純なシステムですが、興味深い動的システムを作成するので、その明白な単純さにだまされるべきではありません。これを出発点として使用して、いくつかの基本的な制御理論を紹介し、継続的な制御強化学習と対比します。その前に、下振り子のモーションモデルとそのモーションをシミュレートする方法を理解する必要があります。
概要
振り子システムの動的モデルを導出し、Pythonのアンサンブルパッケージとオイラー法をそれぞれ使用して2つのシミュレーションモデルを作成しました。機械制御システムの多くの関節やシステムは、単純な振り子でモデル化できるため、ここでのシミュレーションモデルは、複雑なシステムを分析するための基礎として役立ちます。
元のテキストは、記事の数式表示によりわかりやすくなっています。ここをクリックして読むことができます。
振り子ダイナミクス
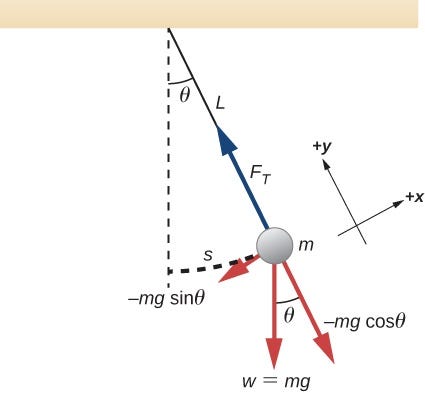
振り子システムをシミュレートするには、最初に振り子のダイナミクスを理解する必要があります。まず、振り子系の力解析図を描きます。振り子ロープの長さ、ボールの質量、重力、およびこのシステムに作用するその他の力を次の図に示します。
绘制受力分析图有助于明确所有作用力,确保我们不会有所遗漏。接下来就可以使用牛顿第二运动定律来分析其动力学。牛顿第二运动定律的形式为 F = ma,我们使用其变体——转动定律表达如下:

在这种情况下,τ 是关于原点的扭矩,I 是旋转惯性,α 是角加速度。扭矩由施加在重物上的力的垂直分量 (关于原点的力矩) 给出,旋转惯性即为 I = mL²,角加速度是 θ 的二阶导数。我们可以将这些值代入到上面的牛顿第二定律,可以得到:

为了完整性,我们还可以考虑单摆上的摩擦,这样就得到:

首先要注意的是,由于方程中存在二阶导数 (θ),所以这是一个二阶常微分方程(ODE)。我们希望能将其简化为一阶系统以便对其进行积分和模拟。但这是以复杂度为代价的,因为我们要把单个二阶系统分解成两个一阶方程。在我们现在分析的这种情况下,复杂度的成本并不大,但是对于更复杂的模型,这样处理可能会适得其反。
为此,我们需要引入两个新变量,分别命名为 θ_1 和 θ_2,并将它们定义为:

我们定义 θ˙_2=θ¨ 来简化上述等式
于是可以得出:
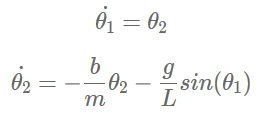
上面的方程式已经准备好了,下面将通过编码来对其进行建模。
模拟单摆动力学
首先导入相关库。
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
复制代码需要先定义一些常量,让质量和长度分别为 1kg 和 1m,至少现在,我们会暂且忽略摩擦,假设 b=0 。我们将模拟单摆从 π/2 (向右升高90度) 的位置开始摆动,并在没有初始速度的情况下释放。我们可以用 0.02s 作为间隔(Δt)来离散化 10s 的时间段。
# 定义常量
m = 1 # 质量 (kg)
L = 1 # 长度 (m)
b = 0 # 摩擦因素 (kg/m^2-s)
g = 9.81 # 重力加速度 (m/s^2)
delta_t = 0.02 # 时间间隔 (s)
t_max = 10 # 最大模拟时长 (s)
theta1_0 = np.pi/2 # 初始角度 (rad)
theta2_0 = 0 # 初始角加速度 (rad/s)
theta_init = (theta1_0, theta2_0)
# 时间序列
t = np.linspace(0, t_max, t_max/delta_t)
复制代码我们将演示两种模拟方法,首先使用 scipy 库进行数值积分,然后再使用欧拉方法。
Scipy 数值积分
使用 scipy 进行数值积分方法,我们需要为模型构建一个积分函数,称为 int_pendulum_sim。该模型将采用 θ_1 和 θ_2 的初始值 (代码中记为 theta_init) 对时间间隔(Δt)进行积分,然后返回对应的 theta 值。这个函数正好就是我们上面推导出的 θ˙_1 和 θ˙_2 的两个方程。
def int_pendulum_sim(theta_init, t, L=1, m=1, b=0, g=9.81):
theta_dot_1 = theta_init[1]
theta_dot_2 = -b/m*theta_init[1] - g/L*np.sin(theta_init[0])
return theta_dot_1, theta_dot_2
复制代码我们可以通过上述将函数作为参数传递给 scipy.integrate.odeint 来对我们的系统进行模拟。并且,还需要给出初始值和模拟时长。
theta_vals_int = integrate.odeint(int_pendulum_sim, theta_init, t)
复制代码函数 odeint 将传入的参数与 θ˙ 进行积分运算,计算结果又作为初始值传入该函数自身以进行下一个时间间隔(Δt)的迭代运算,如此迭代直至所有时间间隔集合被遍历完成。
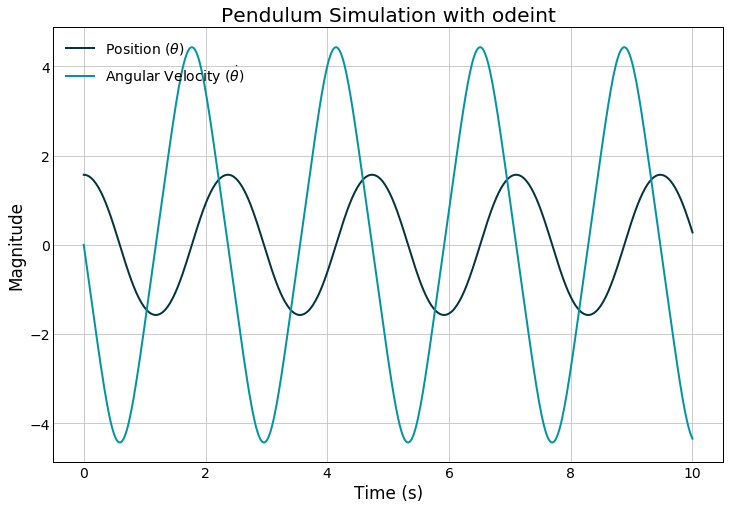
θ 和 θ˙ 随时间变化可以绘制成如下图。
我们的模型中是没有考虑摩擦力或其他力的,所以单摆只会在 -π/2 和 π/2 之间往复地来回摆动。如果增加初始速度,比如:10 rad/s,会看到单摆的运动位置会随着往复来回摆动不断增加。
半隐式欧拉法
通过数值积分来分析这类模型比较简单,但是积分计算的成本相对较大,尤其是处理较大的模型。如果我们想看到模型的长期动态图,我们可以使用欧拉法代替数值积分法来进行模拟。欧拉法也是在 OpenAI 中解决像 Card-Pole 这类控制问题的方法,它能解决强化学习(RL)中的控制问题。
首先需要得到上述常微分方程的泰勒级数展开式。这种计算方法是一种近似法,因此展开式项越多得出的结果也越准确。考虑到当我们当前的场景,只需要扩展到一阶导数并截去高阶项。
首先,需要注意的是我们需要一个关于 θ(t) 的函数。如果我们将 θ(t) 和 t-t_0 代入到泰勒级数展开式(TSE)中,将得到:

其中 O(t²) 表示我们的高阶项,可以在不失去太多准确度的情况下将其删除。请注意,这仅遵循泰勒展开式(TSE)通用公式。有了这个方程,我们可以参考上面的常微分方程代换式,即:

借此,可以将泰勒展开式与常微分方程关联起来:

这样我们就得到了一种更方便的方法,可以在每个时间间隔中更新模型以获取 θ_1(t) 的最新值。重复 θ˙(t) 的展开和替换,可以得到以下结果:

在模拟中遍历的过程中,我们将更新 t_0 作为上一个时间步,并逐步向前移动模型。另外,请注意,这是半隐式欧拉方法 ,这意味着在我们的第二个方程中,我们使用的是最新的 θ_1(t) 而非 θ_1(t_0) 带入到泰勒展开式(TSE)中。我们做出这种微妙的替代是因为,如果没有它,我们的模型将会发散。本质上,我们使用泰勒展开式(TSE)进行的近似计算有一些误差(还记得,前面提到丢弃了那些高阶项)。在这个应用中,这些错误将新能量引入到了的单摆上 —— 这显然违反了热力学第一定律。进行这种替换可以解决所有这些问题。
def euler_pendulum_sim(theta_init, t, L=1, g=9.81):
theta1 = [theta_init[0]]
theta2 = [theta_init[1]]
dt = t[1] - t[0]
for i, t_ in enumerate(t[:-1]):
next_theta1 = theta1[-1] + theta2[-1] * dt
next_theta2 = theta2[-1] - (b/(m*L**2) * theta2[-1] - g/L *
np.sin(next_theta1)) * dt
theta1.append(next_theta1)
theta2.append(next_theta2)
return np.stack([theta1, theta2]).T
复制代码接着运行这个新函数:
theta_vals_euler = euler_pendulum_sim(theta_init, t)
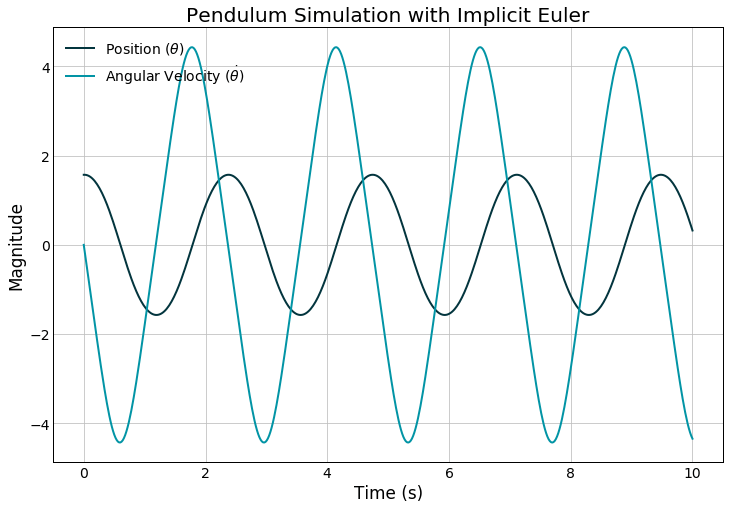
复制代码绘制的图看起来还不错,让我们看下是否和之前方法一的结果相符合。
mse_pos = np.power(
theta_vals_int[:,0] - theta_vals_euler[:,0], 2).mean()
mse_vel = np.power(
theta_vals_int[:,1] - theta_vals_euler[:,1], 2).mean()
print("MSE Position:\t{:.4f}".format(mse_pos))
print("MSE Velocity:\t{:.4f}".format(mse_vel))
MSE Position: 0.0009
MSE Velocity: 0.0000
复制代码不同方法之间的均方误差非常接近,这说明我们得到了一个很好的近似值。
我们使用了两种不同的方法,分别为常微分方程法和欧拉法,其中欧拉法要比常微分方程法 odeint 求解速度快。下面我们来测试并验证一下是否真的速度要快些。
%timeit euler_pendulum_sim(theta_init, t)
2.1 ms ± 82.8 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%timeit integrate.odeint(int_pendulum_sim, theta_init, t)
5.21 ms ± 45.5 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
复制代码与常微分方程的数值积分相比,欧拉方法的速度提高了约 2 倍。
通过以上这些,我们学会了如何使用微积分的第一法则建立和模拟动态模型,并将其应用于一个简单的无摩擦单摆系统。
このような力学系は、自然科学を理解するのに非常に役立ちます。私は最近、同じ手法を使用して、集団内でのウイルスの爆発的な拡散をモデル化する方法を示す記事を書きました。常微分方程式(ODE)は、ロボット工学や工学におけるフィードバック制御やその他の関連アプリケーションにも適しているため、基本的な数値積分の原則を習得する必要があります。
翻訳やその他の改善が必要な分野でエラーを見つけた場合は、ナゲッツ翻訳を修正およびPRしてください。また、対応する報酬ポイントを獲得することもできます。記事の冒頭にあるこの記事への永続的なリンクは、GitHub上のこの記事へのMarkDownリンクです。
ナゲッツ翻訳プロジェクトは、高品質のインターネット技術記事を翻訳するコミュニティです。記事のソースは、ナゲッツに関する英語の共有記事です。コンテンツには、 Android、iOS、フロントエンド、バックエンド、ブロックチェーン、製品、デザイン、人工知能などの分野が含まれます。より高品質の翻訳をご覧になりたい場合は、引き続きNuggetsください。Weibo、およびZhihu列。