1. Théorie des nombres
1.1 nombres premiers
Définition : Tous les nombres naturels supérieurs à 1 sont appelés nombres premiers (nombres premiers) s'ils ne contiennent que deux diviseurs de 1 et de lui-même.
Jugement des nombres premiers : division de première instance
bool is_prime(int n)
{
if(n < 2) return false;
for(int i = 2;i <= n / i;i ++)
{
if(n % i == 0)
return false;
}
return true;
}le premier facteur
Idée de base : énumérer tous les diviseurs de n de petit à grand.
void divide(int n)
{
for(int i = 2;i <= n;i ++)
{
if(n % i == 0)
{
int s = 0;
while(n % i == 0)
{
n /= i;
s ++;
}
printf("%d %d\n",i,s)
}
}
}Méthode du tamis
#include<iostream>
#include<algorithm>
using namespace std;
int primes[N],cnt;
bool st[N];
void get_prime(int n)
{
for(int i = 2;i <= n;i ++)
{
if(!st[i])
{
primes[cnt ++] = n;
for(int j = i + i;j <= n;j += i) st[j] = true;
}
}
}tamis linéaire
Il est garanti que chaque nombre est éliminé par son plus petit facteur premier
#include<iostream>
#include<algorithm>
using namespace std;
int primes[N],cnt;
bool st[N];
void get_primes(int n)
{
for(int i = 2;i<= n;i ++)
{
if(!st[i]) primes[cnt ++] = i;
for(int j = 0;primes[j] <= n / i;j ++)
{
st[primes[j] * i = true;
if(i % primes[j] == 0) break; //primes[j]一定是i的最小质因子
}
}
}1.2 approximation
méthode de division de première instance
vector<int> get_divisors(int n)
{
vector<int> res;
for(int i = 1;i <= n / i;i ++)
if(n % i == 0)
{
res.push_back(i);
if(i != n / i) res.push_back(n / i);
}
sort(res.begin(),res.end());
return res;
}somme des diviseurs et des diviseurs
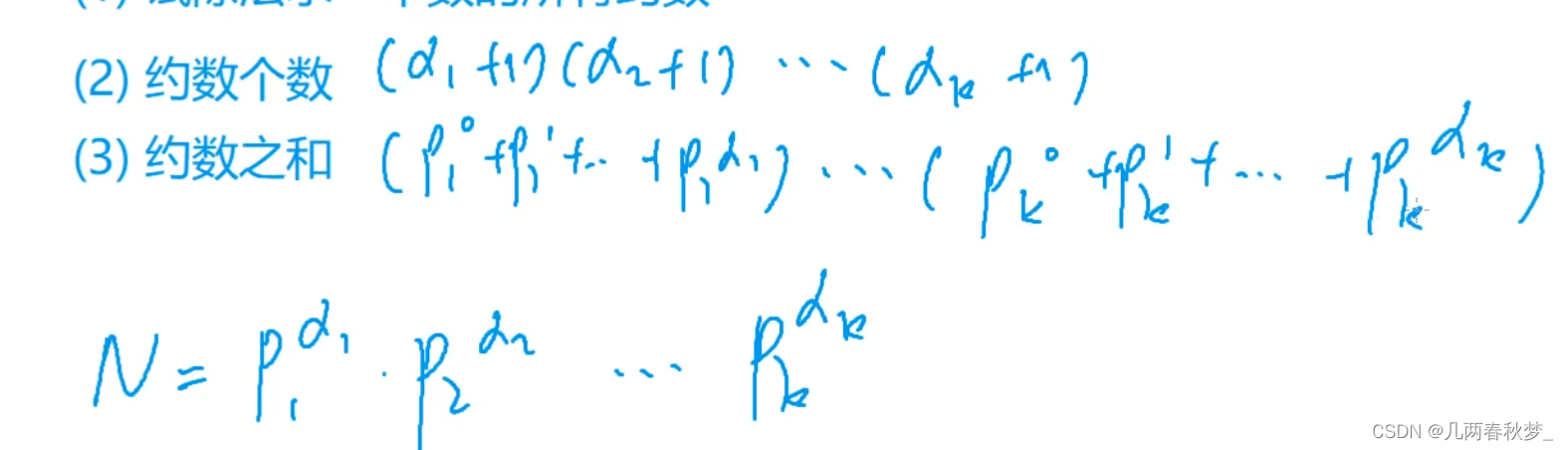
Algorithme euclidien
//返回a与b的最大公约数
int gcd(int a,int b)
{
return b ? gcd(b,(a % b) : a);
}
2. Théorème d'Euler
2.1 Fonction d'Euler
Définition : X(n) représente le nombre de 1~n qui est premier par rapport à n
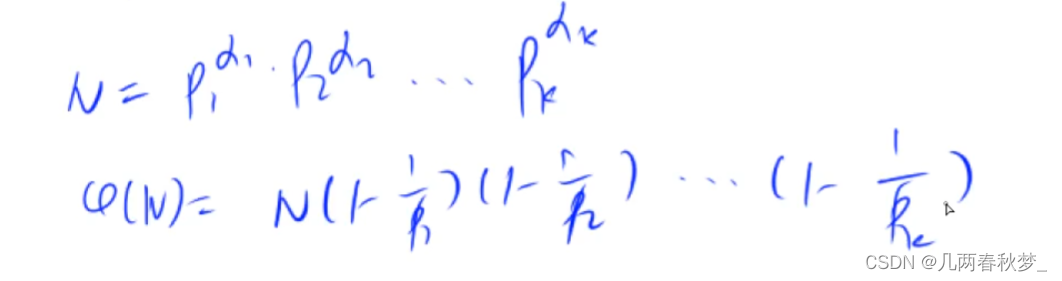
Étapes de l'algorithme :
- Supprimer les multiples de p1,p2,...,pk de 1~N
- plus tous les multiples de Pi*Pj
- Soustraire tous les multiples de Pi*Pj*Pk
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int main()
{
int n;
cin>>n;
while(n --)
{
int a;
cin>>a;
int res = a;
//分解质因数
for(int i = 2 ;i <= a;i ++)
{
if(a % i == 0)
{
res = res / i * (i - 1);
while (a % i == 0) a /= i;
}
}
if(a > 1) res = res / a * (a - 1);
cout<<res<<endl;
}
return 0;
}
puissance rapide
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
//求a^k % p
int main(int a,int k,int p)
{
int res = 1;
while(k)
{
//如果当前k的末位为1,则
if( k & 1) res = (LL)res * a % p;
//删除k的末位
k >>= 1;
//把a平方
a = (LL) a * a % p;
}
return res;
}
int main()
{
int n;
scanf("%d",&n);
while(n --)
{
int a,k,p;
scanf("%d%d%d",&a,&k,&p);
printf("%d\n",qmi(a,k,p));
}
return 0;
}