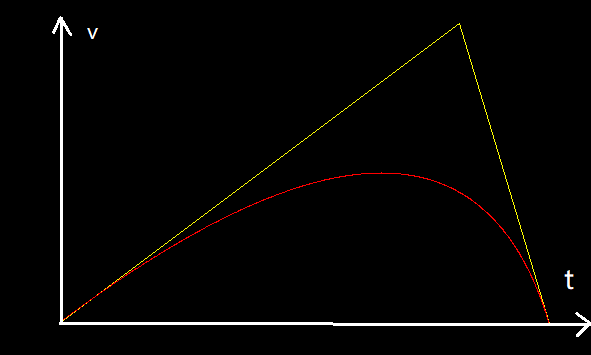
L'animation non linéaire est largement utilisée dans les programmes, les jeux et les animations, alors comment devrions-nous l'implémenter ?
Les points de l'animation non linéaire sont non linéaires sur la ère image, c'est-à-dire qu'il ne s'agit pas d'une fonction linéaire, mais d'une courbe continue partout
Pour que cette courbe puisse être simulée, on utilise ici la courbe de Bézier
1. Introduction de base
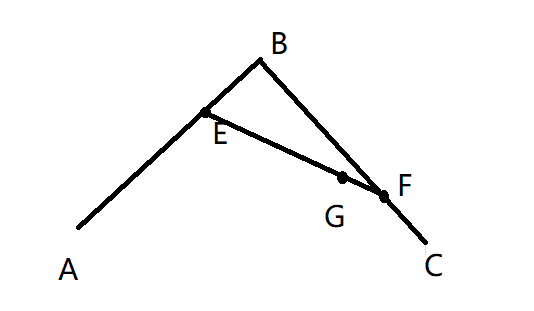
A un certain instant ts, AE/AB=BF/BC=EG/EF
Imaginez qu'il y a des points A, B, C dans le plan, et qu'il y a des points mobiles E, F sur les segments de droite AB, CB respectivement, et la distance entre E, F et son point de départ (A, B) représente la même proportion du segment de droite dans un certain laps de temps, sur la droite Il y a un point G sur le segment EF, son mécanisme est le même que celui de E et F, et il est concevable que la trajectoire de mouvement du point G forme une courbe
C'est la courbe de Bézier quadratique
Deuxième interpolation linéaire
Ok, vous avez déjà une compréhension de base de ce que nous faisons, qui consiste à simuler la trajectoire du point G pour compléter la simulation de la courbe
Pour terminer cette tâche, il faut obtenir la trajectoire du point G. Nous avons besoin d'une fonction qui décrit le mouvement d'une seule puce :
fonction lerp
Il y a deux points fixes AB dans le plan du repère cartésien yOx, le point E est le point mobile se déplaçant sur le segment de droite AB
Si w=AE/AB, w∈[0, 1.0]
Facile à obtenir le vecteur OE=OA+AE
∵AE=wAB
∴OE=OA+wAB
Autrement dit, pour la structure Point E=A+w(BA)=A-wA+wB=(1-w)A+wB
Il existe une fonction f(A, B, w)=(1-w)A+wB
Cette fonction décrit le mouvement du point mobile E sur le segment de droite AB en 1s (w est le temps, w∈[0, 1.0])
Cette fonction est appelée interpolation linéaire, notée lerp(A, B, t)
Troisièmement, trouvez la trajectoire du point G
Nous avons essentiellement terminé la fonction universelle décrivant l'état de mouvement d'un point d'interpolation linéaire, et maintenant nous l'utilisons pour compléter la trajectoire de mouvement du point G
E=lerp(A, B, t) , F=lerp(B ,C, t)
t est le temps pour décrire le mouvement, entre 0-1s, et il peut également être considéré comme le w (poids de poids pour chaque point d'interpolation linéaire, qui est AE/AB=BF/BC=EG/EF), donc nous garantissons Égalité de mouvement pour chaque point d'insertion de segment de ligne ---- se déplacer en même temps à t = 0 et s'arrêter en même temps à t = 1
De même, G=lerp(E, F, t)
Donc la trajectoire du point G est prête à sortir :
E=lerp(A, B, t)
F=lerp(B ,C, t)
G=lerp(E, F, t)
G=lerp(lerp(A, B, t) , lerp(B ,C, t), t)
=> G=lerp((1-t)A+tB, (1-t)B+tC, t)
=(1-t)[(1-t)A+tB]+t[(1-t)B+tC]
=(1-t)^2 A+2t(1-t)B+t^2 C
C'est l'équation quadratique de la courbe de Bézier , et de même pour la cubique
Simulons-le en C++ :
code afficher comme ci-dessous:
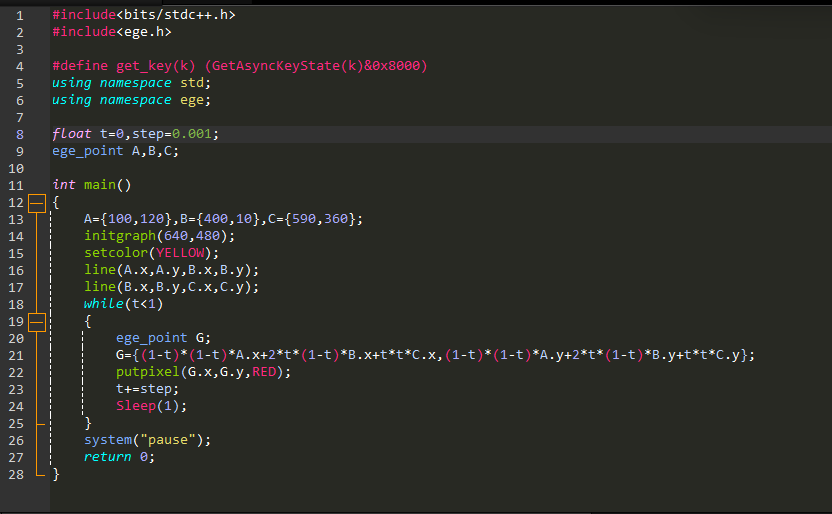
La trajectoire du point G est sur la ligne 21, l'IDE est Red Panda C++, l'environnement est Win11 et la bibliothèque de dessin est EGE
Effet:
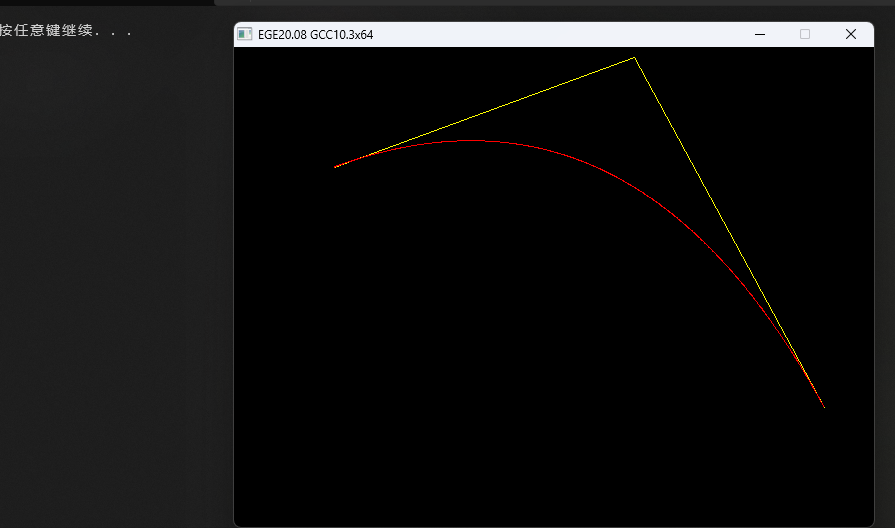
Eh bien, d'une manière générale, l'effet n'est pas mauvais.
Ensuite, avec l'équation de la courbe, nous pouvons commencer à faire de la non-linéarité
Quatre animations non linéaires
Ici, nous prenons la courbe de Bézier quadratique comme exemple
Si vous voulez obtenir un effet non linéaire, vous devez rendre la vitesse de déplacement du personnage non linéaire (non-sens)
Même si la vitesse de l'objet change avec le temps (l'accélération change) : v/t=a≠C
Mettez la courbe de Bézier sur le système de coordonnées vt avec A comme origine, laissez Ay = Cy, évidemment c'est un film non linéaire
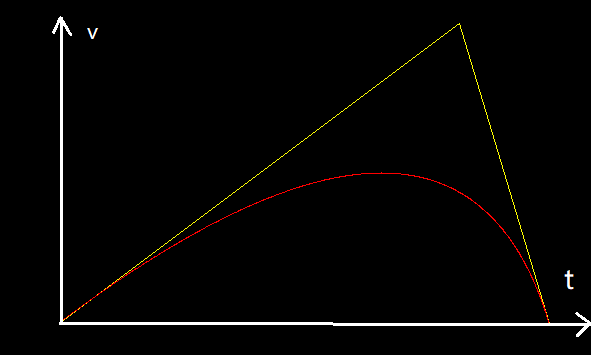
La ligne rouge est la trajectoire du point G obtenue
Étiquetez la ligne rouge comme la fonction g(t)
On peut alors savoir à partir d'une simple connaissance différentielle
Accélération du mouvement des caractères a=v/t=lim(Δt→0) g(t+Δt)/Δt
Comme la taille du pas est limitée, et que l'animation n'a pas besoin d'être trop précise, on prend ici Δt=step (taille du pas, je l'ai mis à 0.001 dans le programme)
Alors l'accélération a=(Gy-G'y)/(Gx-G'.x)
G' fait ici référence à la position de G dans l'étape précédente (la dernière unité est souvent dans l'étape)
De cette façon, nous avons complété le changement d' accélération par la courbe de Bézier quadratique
Cela signifie que nous pouvons l'utiliser pour modifier la vitesse instantanée à laquelle un objet se déplace (accélération), de sorte que la vitesse de l'objet change continuellement au fil du temps à mesure qu'il se déplace.
De cette façon, nous n'avons qu'à ajouter l'accélération de la vitesse de mouvement de l'objet à chaque rafraîchissement pour obtenir la non-linéarité :
L'effet n'est pas affiché
code afficher comme ci-dessous:

Essayez de le copier vous-même :
#include<bits/stdc++.h>
#include<ege.h>
#define get_key(k) (GetAsyncKeyState(k)&0x8000)
using namespace std;
using namespace ege;
float t = 0, step = 0.01;
ege_point A, B, C;
ege_point G = {0.0, 0.0}, nG = {100000, 1};
float v = 0.0, x = 1280, y = 240, r = 10;
float wt = 1, wv = 0.1; //wt偏移调整加速度和曲线相关性 wv速度缩放值
int main() {
A = {0, 480}, B = {240, 0}, C = {480, 480};
initgraph(2560, 480);
getch();
setcolor(YELLOW);
while (t < 1) {
G = {(1 - t)*(1 - t)*A.x + 2 * t*(1 - t)*B.x + t*t * C.x, (1 - t)*(1 - t)*A.y + 2 * t*(1 - t)*B.y + t*t * C.y};
float delta = (G.y - nG.y) / (G.x - nG.x);
nG = G;
t += step;
Sleep(0);
cleardevice();
circle(x, y, r);
v += (wt * delta);
x += (v * wv);
cout << "delta_v " << v << endl;
}
system("pause");
return 0;
}Cinq, conclusion
Dans ce didacticiel, nous avons suivi le processus de découverte de problèmes → problèmes abstraits → construction de modèles → résolution de problèmes → applications pratiques . C'est notre progrès commun
Nous utilisons également la connaissance de l'accélération, des fonctions, des dérivées, des équations, etc. pour traiter des problèmes. C'est un saut important dans notre capacité à appliquer et à résoudre des problèmes de manière globale !