Annuaire d'articles
Introduction de base aux graphiques
Une table linéaire est limitée à une relation entre un prédécesseur direct et un successeur direct, et un arbre ne peut avoir qu'un prédécesseur direct, c'est-à-dire un nœud parent. Lorsque nous devons représenter une relation plusieurs à plusieurs, nous utilisons ici un graphe.
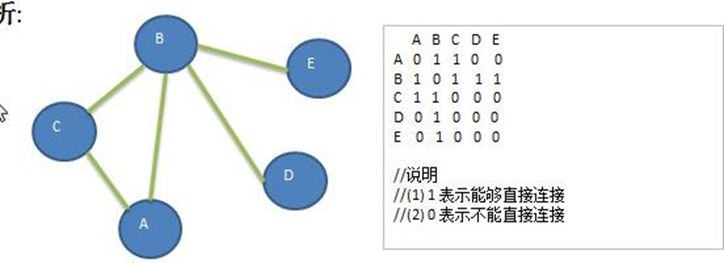
Un graphe est une structure de données dans laquelle un nœud peut avoir zéro ou plusieurs éléments adjacents. Une connexion entre deux nœuds est appelée une arête. Les nœuds peuvent également être appelés sommets. Comme indiqué sur l'image :
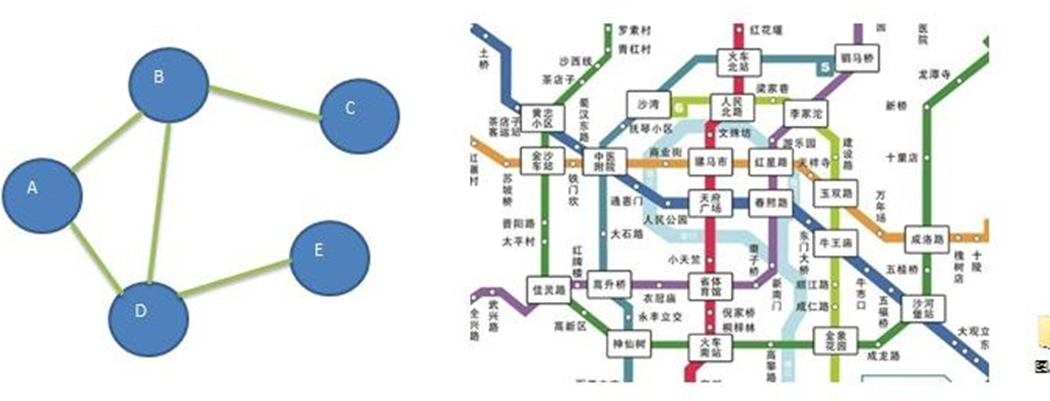
En termes simples, un graphe est un ensemble constitué d'un ensemble fini non vide de sommets et d'arêtes entre eux. Habituellement exprimé sous la forme : G(V,E), où G représente un graphe, V représente une collection de sommets et E représente une collection d'arêtes.
Ensuite, nous parlons de certains concepts communs dans la figure :
-
节点(Vertex): L'élément de base dans le diagramme, utilisé pour représenter une entité. -
边(Edge): un segment de ligne reliant deux nœuds, utilisé pour représenter la relation entre les nœuds. -
度(Degree): Le degré indique le nombre d'arêtes que contient un sommet. Dans un graphe orienté, il est également divisé en degrés sortants et degrés entrants. Le degré sortant indique le nombre d'arêtes sortant du sommet, et le degré entrant indique le nombre d'arêtes entrant dans le sommet. -
有向图和无向图: Le fait que l'arête ait une direction détermine si le graphe est dirigé ou non. L'arête dirigée indique le point de départ et le point d'arrivée de l'arête, et les deux nœuds de l'arête non dirigée n'ont aucune distinction entre le point de départ et le point d'arrivée.
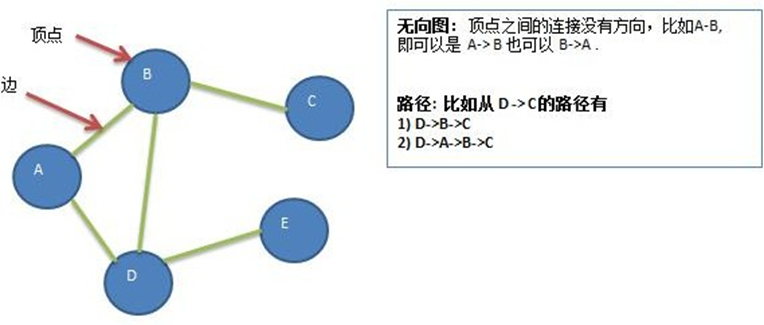
-
带权图和无权图: Le fait que l'arête ait une valeur de poids détermine si le graphique est un graphique pondéré ou un graphique non pondéré. L'arête pondérée a une valeur qui représente le poids de l'arête, et le poids de l'arête non pondérée est considéré comme 1.
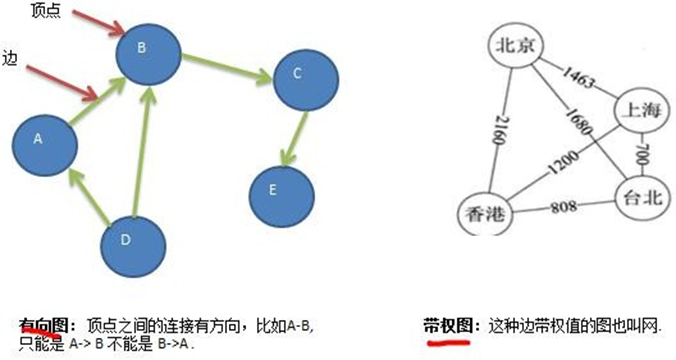
-
路径: Une séquence d'arêtes entre une série de sommets dans un graphe est appelée un chemin. -
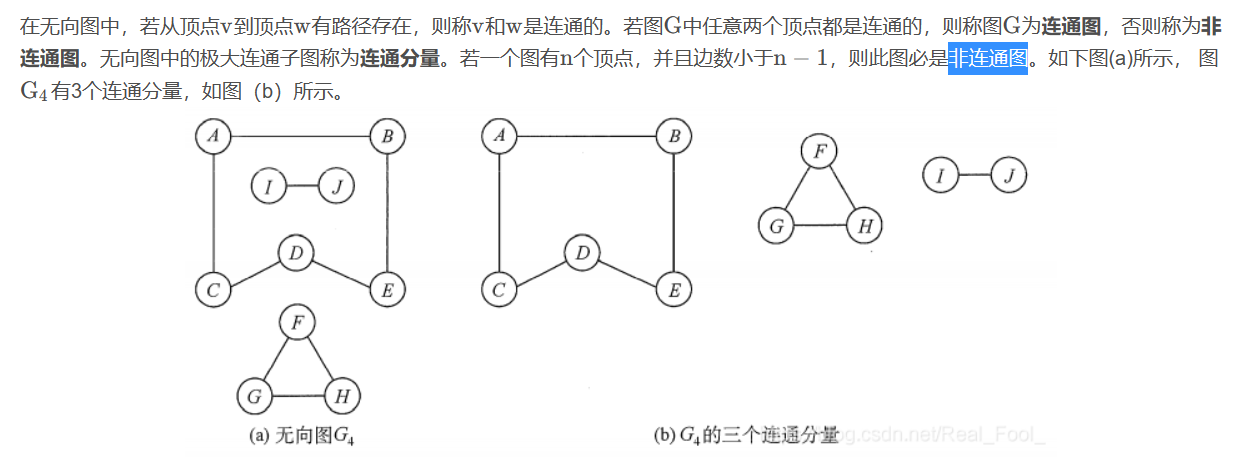
连通性: Un graphe est connexe s'il existe un chemin entre deux nœuds quelconques. Sinon, c'est un graphique déconnecté. -
海量图: Le nombre de nœuds et d'arêtes est énorme, bien au-delà de la taille de la mémoire de l'ordinateur, et nécessite des algorithmes et des structures de stockage spéciaux pour traiter les graphes.
représentation graphique
Il existe deux manières de représenter les graphiques :
- Représentation de tableau à deux dimensions (matrice d'adjacence)
- Représentation en liste chaînée (liste de contiguïté)
matrice de contiguïté
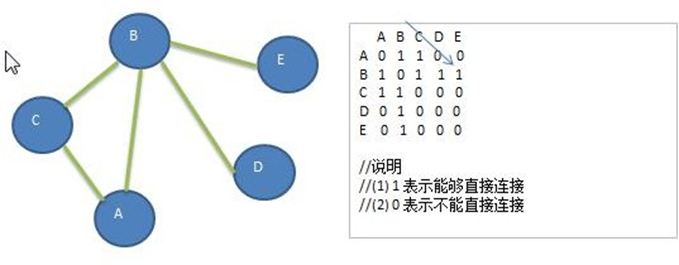
La matrice d'adjacence est une structure de stockage de graphe, qui utilise un tableau à deux dimensions pour représenter les arêtes entre les nœuds du graphe.
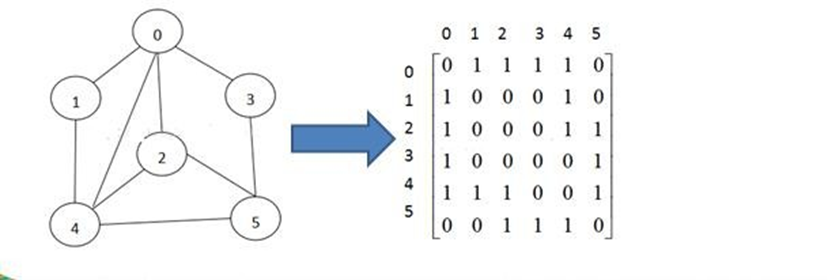
Spécifiquement:
- Le nombre de lignes et de colonnes de la matrice d'adjacence est le nombre n de nœuds dans le graphe.
- Chaque élément de la matrice représente une arête. S'il y a une arête entre le nœud i et le nœud j, l'élément de la ligne i et de la colonne j de la matrice est 1, sinon il est 0.
- Pour les graphiques pondérés, les éléments de la matrice sont les poids correspondants, et non 1.
- Les éléments sur la diagonale principale de la matrice sont tous 0, car le nœud ne sera pas connecté à lui-même.
- La matrice d'adjacence est adaptée pour représenter des graphes denses, et la complexité spatiale est O(n2). Si le graphique est clairsemé, l'utilisation de l'espace est relativement faible.
Les avantages d'une matrice d'adjacence sont :
- Il peut être déterminé en un temps O(1) s'il y a un bord entre deux nœuds quelconques.
- Il est pratique d'implémenter certains algorithmes, tels que la recherche en largeur d'abord, la recherche en profondeur d'abord, etc.
Les inconvénients d'une matrice d'adjacence sont :
- La complexité de l'espace est élevée et si le graphe est clairsemé, cela entraînera un gaspillage d'espace.
- Il est difficile de représenter un graphe dynamique. Si des arêtes sont fréquemment ajoutées et supprimées, la matrice d'adjacence doit être fréquemment reconstruite.
liste de contiguïté
La liste d'adjacence est une autre structure de stockage du graphe, qui utilise une liste chaînée pour stocker les nœuds adjacents de chaque nœud.
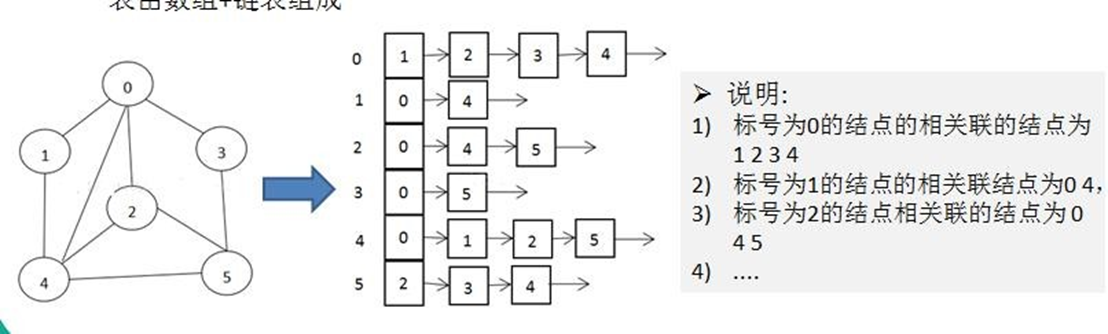
Spécifiquement:
- Les listes de contiguïté sont composées de tableaux et de listes chaînées. Chaque élément du tableau est une liste chaînée, qui représente la liste des nœuds adjacents du nœud correspondant.
- L'indice du tableau est le numéro de série du nœud et la taille du tableau est le nombre de nœuds n.
- Si le nœud i a une arête avec le nœud j, ajouter j à la liste chaînée correspondant à i.
- Pour les graphes pondérés, les éléments de chaque nœud de la liste chaînée ne stockent plus seulement le numéro de série du nœud adjacent, mais stockent une structure, incluant le numéro de série du nœud adjacent et le poids correspondant.
- La liste d'adjacence convient aux graphes clairsemés et la complexité spatiale est O(n+e), où e est le nombre d'arêtes. Pour les graphes denses, le taux d'utilisation de l'espace sera plus élevé.
Les avantages de la liste d'adjacence sont les suivants :
6. La complexité spatiale est faible et convient à la représentation de graphes creux.
7. Il est facile de réaliser l'opération d'ajout et de suppression de graphiques dynamiques.
Les inconvénients de la liste d'adjacence sont :
8. Il est difficile de juger s'il y a un bord entre deux nœuds quelconques en temps O(1), et la liste chaînée doit être parcourue.
9. Il n'est pas pratique d'implémenter certains algorithmes, tels que la recherche en largeur d'abord et la recherche en profondeur d'abord.
Parcours en profondeur (DFS) des graphes
Le soi-disant parcours de graphe est l'accès aux nœuds. Un graphe a tellement de nœuds, comment parcourir ces nœuds nécessite une stratégie spécifique, généralement il y a deux stratégies d'accès :
深度优先遍历(DFS)广度优先遍历(BFS)
aperçu
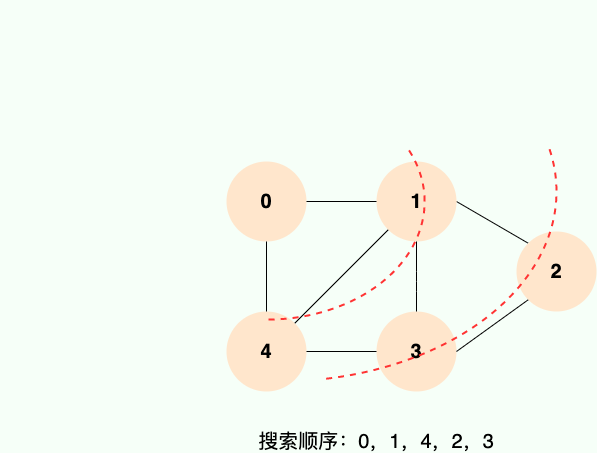
Traversée en profondeur d'abord, à partir du nœud d'accès initial, le nœud d'accès initial peut avoir plusieurs nœuds adjacents, la stratégie de traversée en profondeur d'abord consiste à visiter d'abord le premier nœud adjacent, puis à utiliser le nœud adjacent visité comme nœud initial pour visiter son premier nœud adjacent.
Cela peut être compris comme suit : chaque fois après avoir visité le nœud courant, visitez d'abord le premier nœud adjacent du nœud courant. Nous pouvons voir qu'une telle stratégie d'accès consiste à creuser plus profondément verticalement au lieu d'accéder horizontalement à tous les nœuds adjacents d'un nœud. De toute évidence, la recherche en profondeur est un processus récursif
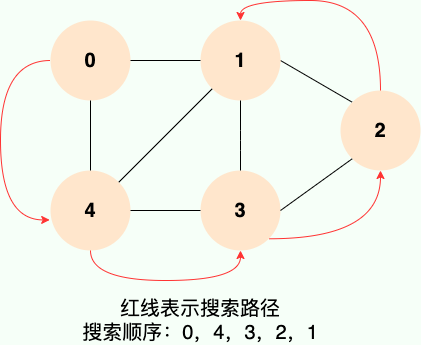
En général : Depth-First Search (Depth-First Search) est un algorithme de parcours de graphe. Il commence à partir d'un certain nœud et recherche aussi profondément que possible jusqu'à ce que tous les nœuds du chemin actuel soient traversés. Revenez ensuite en arrière, en continuant à chercher le chemin suivant le plus profondément possible .
La principale application de la recherche en profondeur estVérification de la connectivité des graphes, tri topologique, résolution du nombre de coupes et résolution du nombre maximal de correspondances de graphes bipartis, etc.。
Étapes de mise en œuvre
Le processus de recherche en profondeur peut être mis en œuvre de manière récursive. Les principales étapes sont les suivantes :
- À partir d'un nœud v dans le graphe cible, visitez le nœud.
- Si le nœud voisin w de v n'a pas été visité, visitez récursivement w.
- Si w a été visité, retournez au nœud v et visitez un autre nœud adjacent non visité de v.
- Si tous les nœuds adjacents de v ont été visités, revenir au nœud précédent de v.
- Répétez les étapes 3 et 4 jusqu'à ce que tous les nœuds soient visités.
Puisque la récursivité est utilisée, nous pouvons certainement utiliser l'idée de pile pour comprendre :
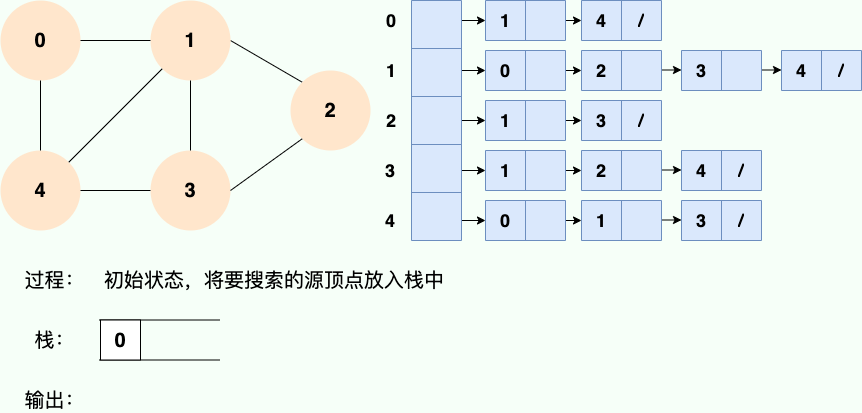
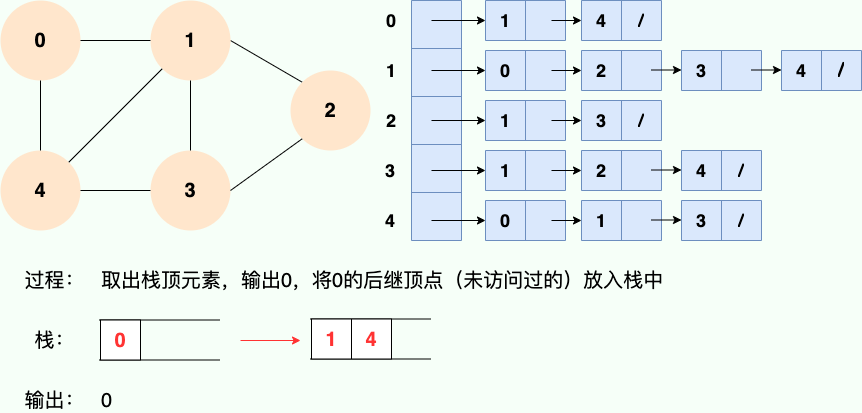
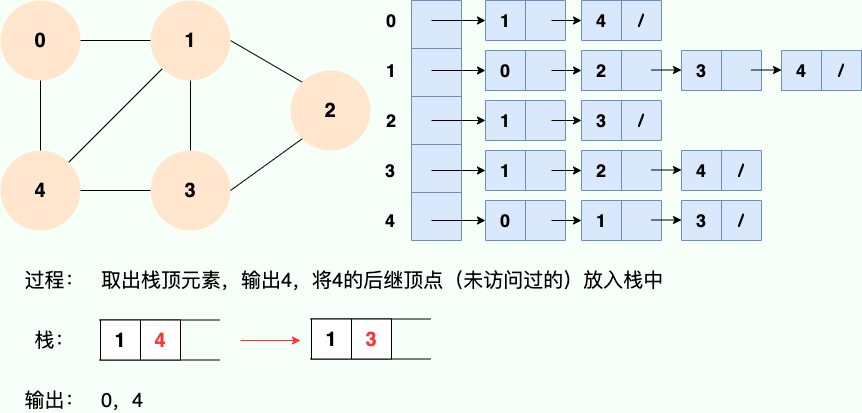
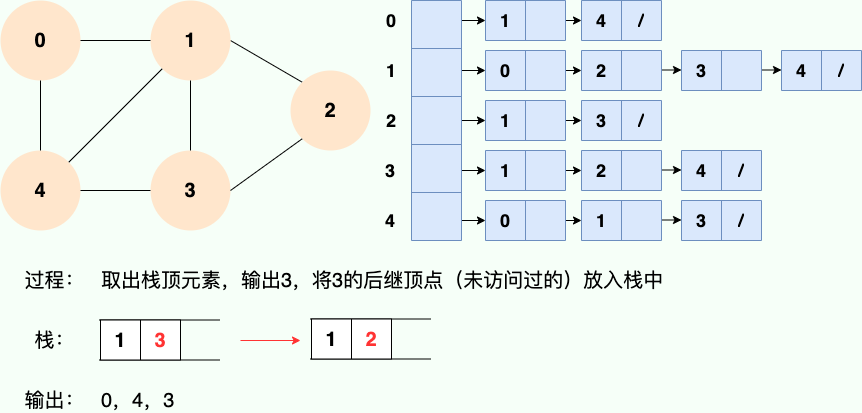
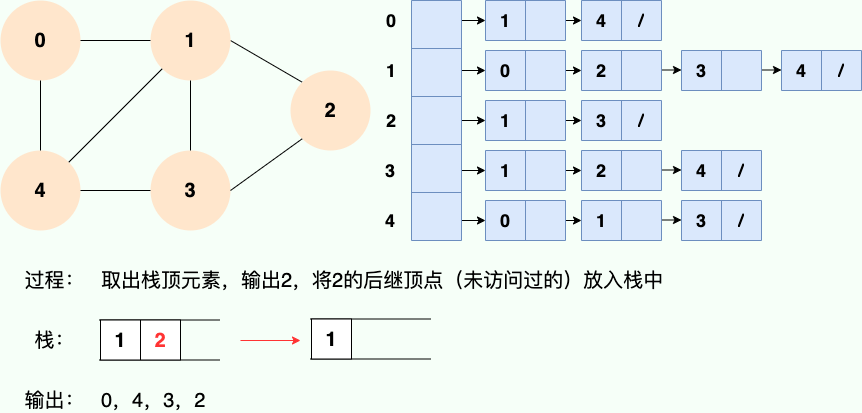
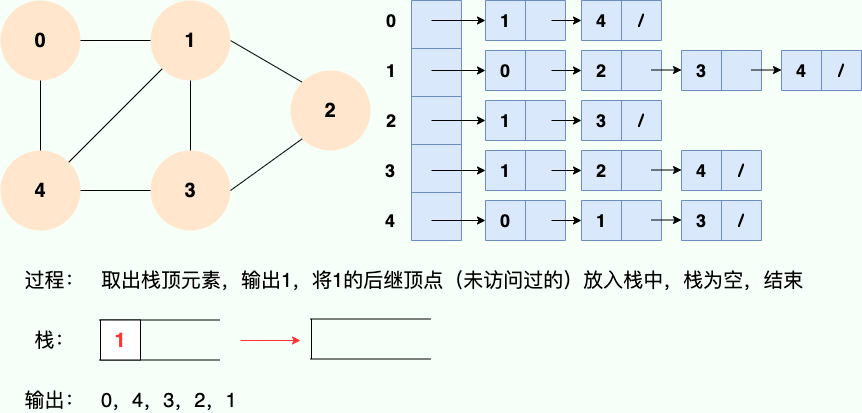
Code
public class Graph {
//存储顶点集合
private ArrayList<String> vertexList;
//存储图对应的邻结矩阵
private int[][] edges;
//表示边的数目
private int numOfEdges;
//定义给数组 boolean[], 记录某个结点是否被访问
private boolean[] isVisited;
//dfs部分
public void dfs(){
//初始化访问数组
isVisited = new boolean[vertexList.size()];
for (int i = 0;i < isVisited.length;i++) {
if (!isVisited[i]) {
dfs(i);
}
}
}
public void dfs(int index){
//打印出当前节点
System.out.print(getValueByIndex(index) + " -> ");
//设置当前节点已被访问
isVisited[index] = true;
//找出该节点的第一个邻接点
int firstNeighbor = getFirstNeighbor(index);
//说明存在第一个临界点
if (firstNeighbor != -1) {
dfs(firstNeighbor);
}
}
/**
* 找到index节点的第一个临界点,如果没有返回-1
* @param index
* @return
*/
public int getFirstNeighbor(int index) {
for (int i = 0; i < edges.length; i++) {
if (edges[index][i] == 1 && !isVisited[i]) {
return i;
}
}
return -1;
}
//返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C"
public String getValueByIndex(int i) {
return vertexList.get(i);
}
}
Avis:
- Dans notre méthode getFirstNeighbor, le j ici doit commencer à partir de 0, et certaines personnes ont tendance à commencer par index+1, ce qui ne tient pas compte de la situation où le parcours ne commence pas à partir de A.
- La raison de traverser notre liste de nœuds est qu'il peut s'agir d'un graphe déconnecté, et traverser à partir d'un nœud peut ne pas traverser tous les nœuds du graphe entier pour
Parcours en largeur d'abord (BFS) des graphes
aperçu
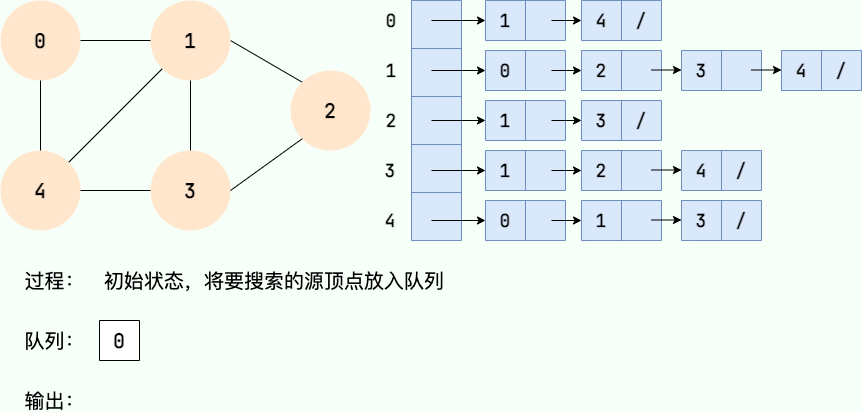
La recherche en largeur d'abord est un algorithme de parcours de graphe. À partir d'un certain nœud, il visite d'abord tous les nœuds adjacents au nœud, puis visite les nœuds adjacents du nœud adjacent, et ainsi de suite, jusqu'à ce que tous les nœuds soient traversés.
La recherche en largeur d'abord s'étend vers l'extérieur couche par couche comme des ondulations sur l'eau :
Par rapport à la recherche en profondeur d'abord, les caractéristiques de la recherche en largeur d'abord sont :
- Les nœuds les plus proches du nœud de départ seront visités en premier. La recherche en profondeur d'abord effectuera une recherche aussi profonde que possible, éventuellement plus loin du point de départ.
- Implémenté à l'aide d'une file d'attente, la complexité de l'espace est élevée. La recherche en profondeur utilise une pile récursive avec une faible complexité spatiale.
La recherche en largeur est principalement utilisée pourLe problème du plus court chemin dans les graphes, tri topologiqueattendez.
Étapes de mise en œuvre
Le processus de recherche en largeur peut être mis en œuvre avec une file d'attente. Les principales étapes sont les suivantes :
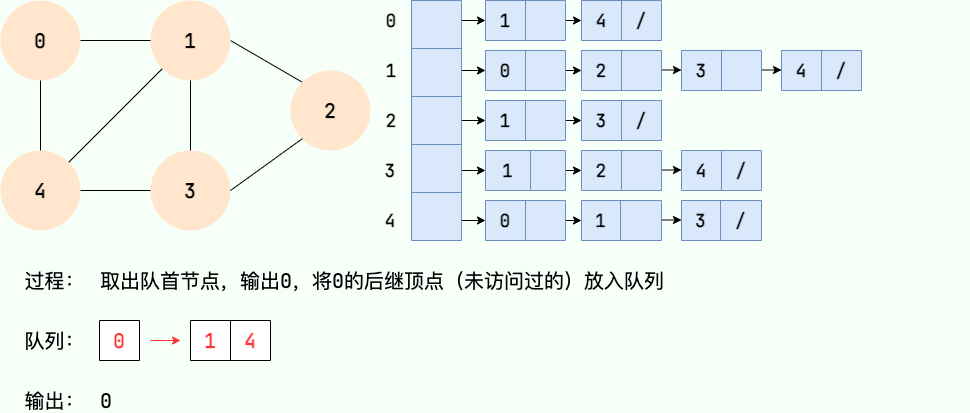
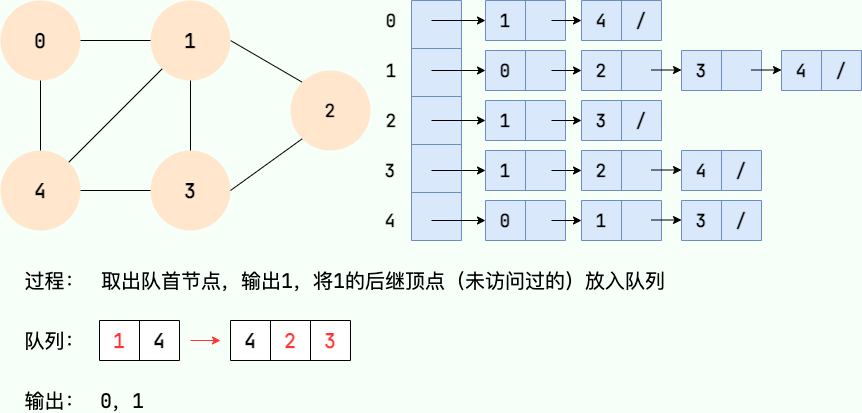
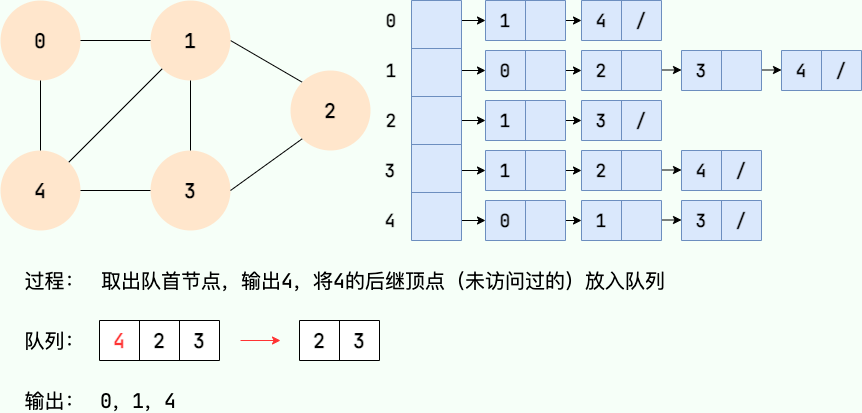
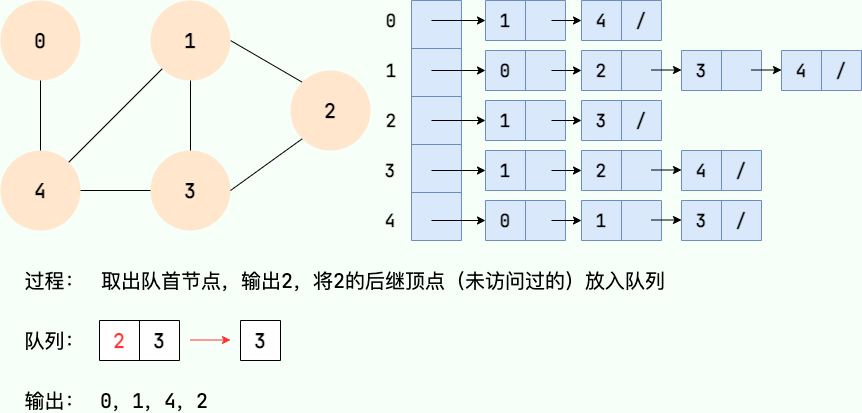
- À partir d'un certain nœud v dans le graphe, visitez le nœud et mettez-le en file d'attente.
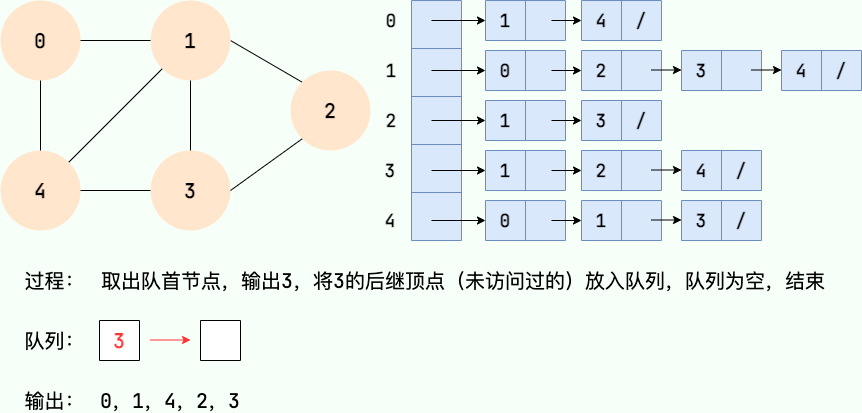
- Sortez le nœud principal de l'équipe, visitez tous les nœuds adjacents non visités de ce nœud et mettez les nœuds adjacents en file d'attente.
- Répétez l'étape 2 jusqu'à ce que la file d'attente soit vide.
- S'il y a des nœuds non visités dans le graphique, commencez par l'un des nœuds non visités et répétez les étapes 1 à 3.
Code
public class Graph {
//存储顶点集合
private ArrayList<String> vertexList;
//存储图对应的邻结矩阵
private int[][] edges;
//表示边的数目
private int numOfEdges;
//定义给数组 boolean[], 记录某个结点是否被访问
private boolean[] isVisited;
/**
* 在bfs中负责找到指定节点的所有未遍历节点
* @param index
*/
public void getNeighbors(int index, Queue<Integer> queue){
for (int i = 0; i < edges.length; i++) {
if (edges[index][i] == 1 && !isVisited[i]) {
queue.add(i);
//将入队节点标为已访问
isVisited[i] = true;
}
}
}
public void bfs(){
//初始化访问数组
isVisited = new boolean[vertexList.size()];
for (int i = 0;i < isVisited.length;i++) {
if (!isVisited[i]) {
bfs(i);
}
}
}
public void bfs(int index) {
//创建队列
Queue<Integer> queue = new LinkedList<>();
//首先将起始节点加入队列,并设为已访问
queue.add(index);
isVisited[index] = true;
//每次弹出的队头
Integer head;
while (!queue.isEmpty()) {
//弹出头节点
head = queue.poll();
//并将其临界点全部放入队列
getNeighbors(head,queue);
//打印该节点
System.out.print(getValueByIndex(head) + " -> ");
}
}
//返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C"
public String getValueByIndex(int i) {
return vertexList.get(i);
}
//返回结点的个数
public int getNumOfVertex() {
return vertexList.size();
}
}
Résumé des codes communs pour les graphiques
public class Graph {
private ArrayList<String> vertexList; //存储顶点集合
private int[][] edges; //存储图对应的邻结矩阵
private int numOfEdges; //表示边的数目
private boolean[] isVisited; //记录某个结点是否被访问
public static void main(String[] args) {
//测试一把图是否创建ok
int n = 8; //结点的个数
//String Vertexs[] = {"A", "B", "C", "D", "E"};
String Vertexs[] = {
"1", "2", "3", "4", "5", "6", "7", "8"};
//创建图对象
Graph graph = new Graph(n);
//循环的添加顶点
for(String vertex: Vertexs) {
graph.insertVertex(vertex);
}
//添加边
//A-B A-C B-C B-D B-E
// graph.insertEdge(0, 1, 1); // A-B
// graph.insertEdge(0, 2, 1); //
// graph.insertEdge(1, 2, 1); //
// graph.insertEdge(1, 3, 1); //
// graph.insertEdge(1, 4, 1); //
//更新边的关系
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 1);
graph.insertEdge(1, 3, 1);
graph.insertEdge(1, 4, 1);
graph.insertEdge(3, 7, 1);
graph.insertEdge(4, 7, 1);
graph.insertEdge(2, 5, 1);
graph.insertEdge(2, 6, 1);
graph.insertEdge(5, 6, 1);
//显示一把邻结矩阵
graph.showGraph();
//测试一把,我们的dfs遍历是否ok
System.out.println("深度遍历");
graph.dfs(); // A->B->C->D->E [1->2->4->8->5->3->6->7]
// System.out.println();
System.out.println("广度优先!");
graph.bfs(); // A->B->C->D-E [1->2->3->4->5->6->7->8]
}
//构造器
public Graph(int n) {
//初始化矩阵和vertexList
edges = new int[n][n];
vertexList = new ArrayList<String>(n);
numOfEdges = 0;
}
//得到第一个邻接结点的下标 w
/**
*
* @param index
* @return 如果存在就返回对应的下标,否则返回-1
*/
public int getFirstNeighbor(int index) {
for(int j = 0; j < vertexList.size(); j++) {
if(edges[index][j] > 0) {
return j;
}
}
return -1;
}
//根据前一个邻接结点的下标来获取下一个邻接结点
public int getNextNeighbor(int v1, int v2) {
for(int j = v2 + 1; j < vertexList.size(); j++) {
if(edges[v1][j] > 0) {
return j;
}
}
return -1;
}
//深度优先遍历算法
//i 第一次就是 0
private void dfs(boolean[] isVisited, int i) {
//首先我们访问该结点,输出
System.out.print(getValueByIndex(i) + "->");
//将结点设置为已经访问
isVisited[i] = true;
//查找结点i的第一个邻接结点w
int w = getFirstNeighbor(i);
while(w != -1) {
//说明有
if(!isVisited[w]) {
dfs(isVisited, w);
}
//如果w结点已经被访问过
w = getNextNeighbor(i, w);
}
}
//对dfs 进行一个重载, 遍历我们所有的结点,并进行 dfs
public void dfs() {
isVisited = new boolean[vertexList.size()];
//遍历所有的结点,进行dfs[回溯]
for(int i = 0; i < getNumOfVertex(); i++) {
if(!isVisited[i]) {
dfs(isVisited, i);
}
}
}
//对一个结点进行广度优先遍历的方法
private void bfs(boolean[] isVisited, int i) {
int u ; // 表示队列的头结点对应下标
int w ; // 邻接结点w
//队列,记录结点访问的顺序
LinkedList queue = new LinkedList();
//访问结点,输出结点信息
System.out.print(getValueByIndex(i) + "=>");
//标记为已访问
isVisited[i] = true;
//将结点加入队列
queue.addLast(i);
while( !queue.isEmpty()) {
//取出队列的头结点下标
u = (Integer)queue.removeFirst();
//得到第一个邻接结点的下标 w
w = getFirstNeighbor(u);
while(w != -1) {
//找到
//是否访问过
if(!isVisited[w]) {
System.out.print(getValueByIndex(w) + "=>");
//标记已经访问
isVisited[w] = true;
//入队
queue.addLast(w);
}
//以u为前驱点,找w后面的下一个邻结点
w = getNextNeighbor(u, w); //体现出我们的广度优先
}
}
}
//遍历所有的结点,都进行广度优先搜索
public void bfs() {
isVisited = new boolean[vertexList.size()];
for(int i = 0; i < getNumOfVertex(); i++) {
if(!isVisited[i]) {
bfs(isVisited, i);
}
}
}
//图中常用的方法
//返回结点的个数
public int getNumOfVertex() {
return vertexList.size();
}
//显示图对应的矩阵
public void showGraph() {
for(int[] link : edges) {
System.err.println(Arrays.toString(link));
}
}
//得到边的数目
public int getNumOfEdges() {
return numOfEdges;
}
//返回结点i(下标)对应的数据 0->"A" 1->"B" 2->"C"
public String getValueByIndex(int i) {
return vertexList.get(i);
}
//返回v1和v2的权值
public int getWeight(int v1, int v2) {
return edges[v1][v2];
}
//插入结点
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
//添加边
/**
*
* @param v1 表示点的下标即使第几个顶点 "A"-"B" "A"->0 "B"->1
* @param v2 第二个顶点对应的下标
* @param weight 表示
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}
}
Algorithme Spanning Tree minimal
L'arbre couvrant minimum est un concept très important dans la théorie des graphes.Il fait référence à un arbre reliant tous les nœuds du graphe, et la somme des poids de toutes les arêtes de cet arbre est la plus petite。
Un arbre couvrant minimum a plusieurs propriétés importantes :
- Il contient tous les nœuds du graphe, il n'y a pas de points isolés.
- C'est un arbre, sans cernes.
- Sa somme de poids est la plus petite.
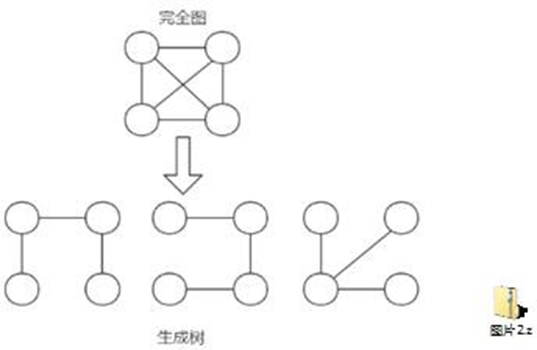
Les algorithmes d'arbre couvrant minimum courants sont :
4. Prim算法: Commencer à partir d'un nœud et ajouter continuellement de nouveaux nœuds et arêtes à l'arbre couvrant jusqu'à ce que tous les nœuds soient inclus. Chaque nouvelle arête ajoutée est l'arête la plus courte d'un nœud dans l'arbre.
5.Kruskal算法 : Sélectionnez l'arête en fonction du poids de l'arête de petit à grand. Tant que cette arête ne forme pas un anneau, elle sera ajoutée à l'arbre couvrant minimum.
6. Dijkstra算法: Utilisez l'algorithme de chemin le plus court de Dijkstra pour trouver le chemin le plus court de chaque nœud à tous les autres nœuds, et l'arbre couvrant minimum est formé par ces chemins les plus courts.
L'arbre couvrant minimum a de nombreuses applications pratiques, telles que la connectivité réseau, le câblage de circuits, etc. Il apporte une solution efficace à ces problèmes pratiques.
En bref, l'arbre couvrant minimum est un concept très classique et important en théorie des graphes, et les algorithmes associés sont également importants, et il vaut la peine de le comprendre et de le maîtriser.
Démonstration de l'animation de l'algorithme Minimum Spanning Tree (Kruskal (Kruskal) et Prim (Prim))
Algorithme de Prim
L'algorithme de Prim est l'un des algorithmes classiques d'arbre couvrant minimum. Son idée de base est :
- À partir de n'importe quel nœud du graphe, ajoutez des arêtes et des nœuds étape par étape pour former un arbre couvrant minimum. Chaque nouvelle arête ajoutée doit connecter des nœuds dans l'arbre et des nœuds hors de l'arbre, et cette nouvelle arête doit être celle qui a le plus petit poids parmi toutes les arêtes candidates.
Les étapes de l'algorithme de Prim sont les suivantes :
- Sélectionnez n'importe quel nœud du graphique comme nœud de départ et marquez que ce nœud a été visité.
- Trouvez une arête avec le plus petit poids parmi tous les nœuds non visités connectés aux nœuds visités. Les nœuds non visités connectés par cette arête sont marqués comme visités.
- Répétez l'étape 2 jusqu'à ce que tous les nœuds soient visités.
- L'ensemble d'arêtes formé est l'arbre couvrant minimum.
Ou vous pouvez vous référer à la vidéo suivante qui l'explique très clairement :
Diagramme d'algorithme :

La complexité temporelle de l'algorithme de Prim est O(n2), et elle peut être réduite à O(nlogn) s'il est implémenté avec une file d'attente prioritaire.
L'algorithme de Prim n'est applicable qu'aux graphes connectés non orientés pondérés. Si le graphe est orienté ou déconnecté, l'algorithme de Prim ne peut pas obtenir l'arbre couvrant minimum.
pratique de l'algorithme
Code:
import java.util.*;
public class PrimAlgorithm {
private static final int INF = Integer.MAX_VALUE;
public static int prim(int[][] graph) {
int n = graph.length;
//创建距离表,代表索引对应节点距离最小生成树的距离
int[] dist = new int[n];
//记录每个节点是否被添加,未添加记为false
boolean[] visited = new boolean[n];
//先将距离表都初始化为最大值
Arrays.fill(dist, INF);
//从0节点开始遍历,将距离更新一下
dist[0] = 0;
//记录要返回的最小权值
int res = 0;
for (int i = 0; i < n; i++) {
//u代表要添加的节点(距离最近且未访问)
int u = -1;
for (int j = 0; j < n; j++) {
if (!visited[j] && (u == -1 || dist[j] < dist[u])) {
u = j;
}
}
//将要添加的节点标为已访问
visited[u] = true;
//记录权值
res += dist[u];
//更新距离表
for (int v = 0; v < n; v++) {
if (!visited[v] && graph[u][v] != INF && graph[u][v] < dist[v]) {
dist[v] = graph[u][v];
}
}
}
return res;
}
public static void main(String[] args) {
int[][] graph = new int[][]{
{
0, 2, INF, 6, INF},
{
2, 0, 3, 8, 5},
{
INF, 3, 0, INF, 7},
{
6, 8, INF, 0, 9},
{
INF, 5, 7, 9, 0}
};
int res = prim(graph);
System.out.println(res);
}
}
Dans cette implémentation, nous initialisons d'abord le tableau de distance dist et le tableau d'indicateurs de visite visités, et initialisons tous les éléments du tableau de distance à l'infini (représentant les nœuds qui n'ont pas été visités).
Ensuite, nous parcourons tous les nœuds à partir du nœud 0, en sélectionnant à chaque fois la plus petite valeur du tableau de distance comme prochain nœud à visiter. Ensuite, nous marquons ce nœud comme visité et mettons à jour sa distance par rapport aux nœuds non encore visités dans le tableau de distance. Enfin, nous renvoyons la somme de tous les poids des arêtes comme poids minimal de l'arbre couvrant.
La complexité temporelle de cette implémentation est O(n^2), où n est le nombre de nœuds.
Algorithme de Kruskal
L'algorithme de Kruskal est un autre algorithme classique pour l'arbre couvrant minimum. Son idée de base est la suivante :
trier toutes les arêtes du graphe en fonction de leur poids, du plus petit au plus grand. Sélectionnez l'arête avec le plus petit poids et ajoutez-la à l'arbre couvrant minimum tant que l'arête ne forme pas de cycle. Répétez cette étape jusqu'à ce que l'arbre couvrant minimum contienne tous les nœuds du graphe.
Les étapes de l'algorithme de Kruskal sont les suivantes :
- Triez toutes les arêtes du graphique par ordre croissant de poids.
- Sélectionnez l'arête avec le plus petit poids pour déterminer si un anneau est formé. S'il ne forme pas de cycle, il est ajouté à l'arbre couvrant minimum.
- Répétez l'étape 2 jusqu'à ce que l'arbre couvrant minimum contienne tous les sommets du graphe.
- Générer un arbre couvrant minimum.
La complexité temporelle de l'algorithme de Kruskal est O(ElogE), où E est le nombre d'arêtes dans le graphe.
L'implémentation de l'algorithme de Kruskal doit utiliser l'ensemble de recherche d'union pour déterminer si l'arête sélectionnée formera un anneau . Le contrôle d'union peut juger si deux éléments appartiennent au même ensemble en temps O (1), ce qui est la clé pour réaliser l'algorithme de Kruskal.
Comparé à l'algorithme de Prim, l'algorithme de Kruskal convient aux graphes creux avec plus d'arêtes, car sa complexité temporelle ne dépend pas du nombre de nœuds, mais uniquement du nombre d'arêtes. Mais l'algorithme de Kruskal doit trier toutes les arêtes à l'avance, ce qui augmente la complexité de l'espace.
Illustration:
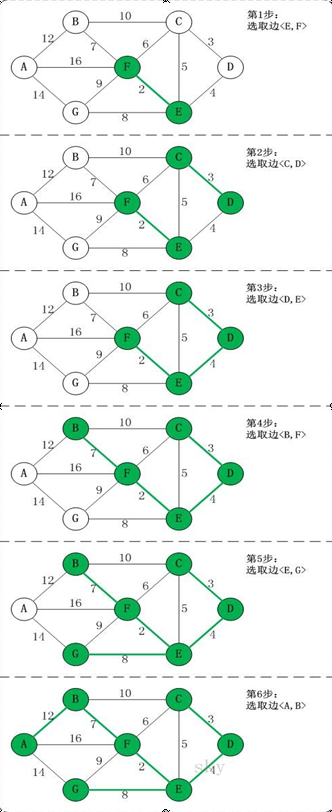
Et rechercher
L'ensemble de contrôle d'union est une structure de données de type arborescent, qui est utilisée pour traiter les problèmes de fusion et de requête de certains ensembles disjoints .
Il prend en charge trois opérations :
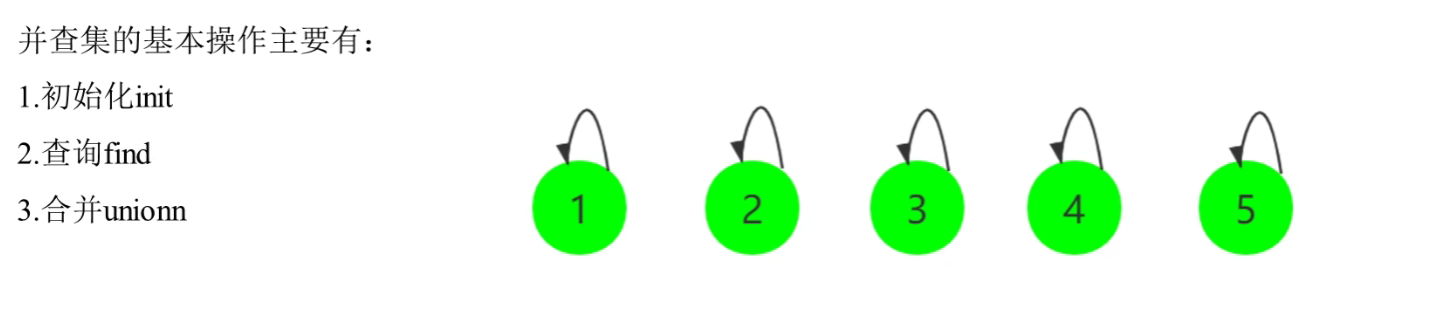
- initialiser init
union(x, y): fusionne la collection où se trouvent l'élément x et l'élément y.find(x): Trouver le représentant de l'ensemble où se trouve l'élément x, et le représentant de l'ensemble est le premier élément ajouté à l'ensemble.
La recherche d'union met en œuvre une sorte de connectivité dynamique. Au début, chaque élément forme un ensemble par lui-même, et les ensembles sont continuellement fusionnés par l'opération d'union, et finalement plusieurs grands ensembles disjoints sont formés.
L'application typique de la recherche d'union consiste à résoudre le problème de requête hors ligne dans la théorie des graphes, par exemple en demandant si deux nœuds se trouvent dans le même graphe connexe dans un graphe non orienté.
Il existe deux manières courantes d'implémenter le contrôle d'union :
- Recherche rapide : à l'aide d'une structure arborescente, l'opération de recherche doit traverser le nœud racine et la complexité temporelle est O(n).
- Fusion rapide avec compression de chemin : pendant le processus de parcours de l'opération de recherche, pointez le nœud directement vers le nœud racine pour obtenir une compression de chemin et réduire la profondeur de l'arborescence. Après équilibrage, la complexité temporelle peut atteindre O(1).

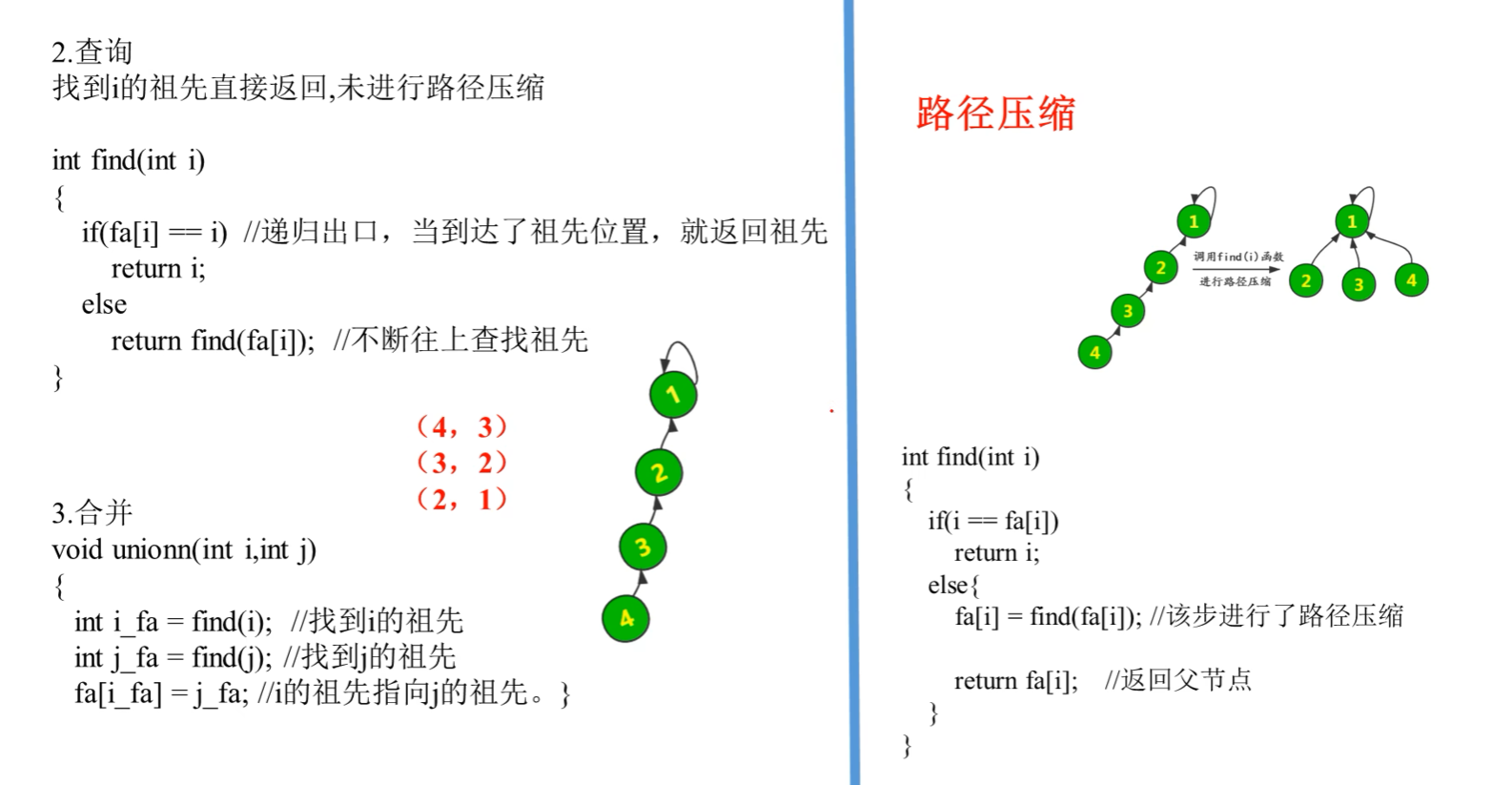
pratique de l'algorithme
import java.util.*;
public class KruskalAlgorithm {
private static class Edge implements Comparable<Edge> {
int u, v, w;
public Edge(int u, int v, int w) {
this.u = u;
this.v = v;
this.w = w;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(this.w, o.w);
}
}
public static int kruskal(int[][] graph) {
int n = graph.length;
List<Edge> edges = new ArrayList<>();
for (int u = 0; u < n; u++) {
for (int v = u + 1; v < n; v++) {
if (graph[u][v] != 0) {
edges.add(new Edge(u, v, graph[u][v]));
}
}
}
Collections.sort(edges);
int[] parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
int res = 0;
for (Edge edge : edges) {
int u = edge.u;
int v = edge.v;
int w = edge.w;
int pu = find(parent, u);
int pv = find(parent, v);
if (pu != pv) {
parent[pu] = pv;
res += w;
}
}
return res;
}
private static int find(int[] parent, int x) {
if (parent[x] != x) {
parent[x] = find(parent, parent[x]);
}
return parent[x];
}
public static void main(String[] args) {
int[][] graph = new int[][]{
{
0, 2, 0, 6, 0},
{
2, 0, 3, 8, 5},
{
0, 3, 0, 0, 7},
{
6, 8, 0, 0, 9},
{
0, 5, 7, 9, 0}
};
int res = kruskal(graph);
System.out.println(res);
}
}
Dans cette implémentation, nous stockons d'abord toutes les arêtes du graphe dans une liste et les trions par ordre croissant de poids. Ensuite, nous initialisons une recherche d'union, en initialisant le parent de chaque nœud à lui-même.
Ensuite, nous parcourons la liste des arêtes triées.Pour chaque arête, si ses deux extrémités ne sont pas dans le même bloc connecté, fusionnez-les dans le même bloc connecté, et ajoutez le poids de cette arête au poids de l'arbre couvrant minimum.
La complexité temporelle de cette implémentation est O(m log m), où m est le nombre d'arêtes.
algorithme du plus court chemin
Démonstration d'animation de l'algorithme de la plus courte distance (chemin le plus court) de la théorie des graphes - Dijkstra (Dijkstra) et Floyd (Floyd)
Algorithme de Dijkstra
L'algorithme de Dijkstra est un algorithme de chemin le plus court typique, qui est utilisé pour calculer le chemin le plus court d'un nœud à d'autres nœuds. Sa principale caractéristique est de s'étendre du point de départ à la couche externe (idée de recherche en largeur d'abord) jusqu'à ce qu'elle atteigne la fin.
L'algorithme de Dijkstra est un algorithme permettant de trouver le chemin le plus court à source unique. Son idée de base est :
- Sélectionnez un nœud comme nœud de départ et calculez le chemin le plus court du nœud de départ aux autres nœuds.
- Parcourez tous les nœuds accessibles à partir du nœud de départ et mettez à jour le chemin le plus court. Sélectionnez le nœud suivant pour continuer à traverser jusqu'à ce que tous les nœuds soient traversés.
- Répétez les étapes ci-dessus jusqu'à ce que le chemin le plus court du nœud de départ à tous les nœuds soit finalement obtenu.
Les étapes de l'algorithme de Dijkstra sont les suivantes :
- Sélectionnez la source du nœud de départ, définissez sa distance sur 0 et définissez la distance des autres nœuds sur l'infini.
- Trouvez le nœud u qui n'est pas dans l'ensemble S et qui a la plus petite distance, et sa distance est dist[u].
- Ajoutez u à l'ensemble S, indiquant que u a été visité.
- En prenant u comme nœud intermédiaire, mettez à jour la distance à son nœud adjacent v. dist[v] = min(dist[v], dist[u] + poids(u, v)).
- Répétez les étapes 2, 3 et 4 jusqu'à ce que S contienne tous les nœuds.
- Générez le chemin le plus court et la distance de chaque nœud.
L'algorithme de Dijkstra utilise un tableau dist pour enregistrer la longueur de chemin la plus courte de chaque nœud et utilise la petite file d'attente prioritaire du tas racine pour trouver le nœud avec la plus petite distance. Les complexités temporelle et spatiale sont respectivement O(nlogn) et O(n).
pratique de l'algorithme
import java.util.*;
public class DijkstraAlgorithm {
private static final int INF = Integer.MAX_VALUE;
public static int[] dijkstra(int[][] graph, int start) {
int n = graph.length;
int[] dist = new int[n];
boolean[] visited = new boolean[n];
Arrays.fill(dist, INF);
dist[start] = 0;
for (int i = 0; i < n; i++) {
int u = -1;
for (int j = 0; j < n; j++) {
if (!visited[j] && (u == -1 || dist[j] < dist[u])) {
u = j;
}
}
visited[u] = true;
for (int v = 0; v < n; v++) {
if (!visited[v] && graph[u][v] != INF && dist[u] + graph[u][v] < dist[v]) {
dist[v] = dist[u] + graph[u][v];
}
}
}
return dist;
}
public static void main(String[] args) {
int[][] graph = new int[][]{
{
0, 2, INF, 6, INF},
{
2, 0, 3, 8, 5},
{
INF, 3, 0, INF, 7},
{
6, 8, INF, 0, 9},
{
INF, 5, 7, 9, 0}
};
int start = 0;
int[] dist = dijkstra(graph, start);
System.out.println(Arrays.toString(dist));
}
}
Dans cette implémentation, nous initialisons d'abord le tableau de distance dist et le tableau d'indicateurs de visite visités, et initialisons tous les éléments du tableau de distance à l'infini (représentant les nœuds qui n'ont pas été visités). Ensuite, nous parcourons tous les nœuds à partir du point de départ, en sélectionnant à chaque fois la plus petite valeur du tableau de distance comme prochain nœud à visiter. Ensuite, nous marquons ce nœud comme visité et mettons à jour sa distance par rapport aux nœuds non encore visités dans le tableau de distance. Enfin, nous renvoyons le tableau de distance.
La complexité temporelle de cette implémentation est O(n^2), où n est le nombre de nœuds. Si la file d'attente prioritaire est utilisée pour optimiser, la complexité temporelle peut être réduite à O(m log n), où m est le nombre d'arêtes.
Algorithme de Floyd
L'algorithme de Floyd est un algorithme permettant de trouver le chemin le plus court entre toutes les paires de nœuds. Son idée de base est :
trouver le chemin le plus court de chaque nœud à tous les autres nœuds par récursivité.
Les étapes de l'algorithme de Floyd sont les suivantes :
- Initialisez le tableau dist,
dist[i][j]représentant la longueur du chemin le plus court du nœud i au nœud j. A ce momenti==j,dist[i][j] = 0; lorsqu'il y a un chemin direct entre le nœud i et le nœud j,dist[i][j]c'est la longueur du chemin ; sinondist[i][j] = ∞. - En traversant chaque nœud intermédiaire k, mettre à jour le tableau dist :
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
cela signifie que le chemin le plus court du nœud i au nœud j peut passer par le nœud k. - Répétez l'étape 2 jusqu'à ce que tous les nœuds intermédiaires aient été traversés.
- Le résultat final du tableau dist est la longueur de chemin la plus courte entre chaque paire de nœuds.
La complexité temporelle et la complexité spatiale de l'algorithme de Floyd sont toutes deux O(n3), où n est le nombre de nœuds.
L'algorithme de Floyd convient pour résoudre le chemin le plus court entre deux nœuds et peut résoudre le problème du chemin le plus court du graphe orienté et du graphe pondéré.
L'algorithme de Dijkstra et l'algorithme de Floyd sont tous deux des algorithmes classiques pour résoudre le problème du plus court chemin, mais ils présentent les principales différences suivantes :
- Types de diagrammes applicables :
- L'algorithme de Dijkstra ne peut être utilisé que pour trouver le chemin le plus court à source unique de graphes orientés ou non orientés, et ne peut pas trouver le chemin le plus court entre deux points.
- L'algorithme de Floyd peut être utilisé pour trouver le chemin le plus court entre deux points quelconques dans un graphe orienté ou non orienté.
- Type de chemin le plus court :
- L'algorithme de Dijkstra trouve un arbre de chemin le plus court et ne peut obtenir que le chemin le plus court d'un point source unique à d'autres points.
- L'algorithme de Floyd calcule le chemin le plus court entre tous les nœuds en même temps et obtient une matrice de chemin le plus court.
- complexité temporelle :
- L'algorithme de Dijkstra est implémenté en utilisant une file d'attente prioritaire et la complexité temporelle est O (nlogn).
- La complexité temporelle de l'algorithme de Floyd est O(n3).
- Lorsque le nombre de nœuds dans le graphe est grand mais que le nombre d'arêtes est petit, l'algorithme de Dijkstra est plus efficace. Lorsque le nombre de nœuds et d'arêtes du graphe est grand, l'algorithme de Floyd est plus efficace.
- Complexité spatiale :
- L'algorithme de Dijkstra ne nécessite que l'espace O(n).
- L'algorithme de Floyd nécessite un espace O(n2) pour stocker la matrice du plus court chemin.
- Un nœud intermédiaire est-il requis :
- L'algorithme de Dijkstra ne prend en compte que le chemin le plus court du point de départ au point final lors de la mise à jour du chemin le plus court, sans informations sur les nœuds intermédiaires.
- L'algorithme de Floyd a besoin d'informations sur les nœuds intermédiaires lors de la mise à jour du chemin le plus court, et le chemin le plus court ne peut être mis à jour que par des sauts de nœuds intermédiaires.
pratique de l'algorithme
import java.util.*;
public class FloydAlgorithm {
private static final int INF = Integer.MAX_VALUE;
public static int[][] floyd(int[][] graph) {
int n = graph.length;
int[][] dist = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dist[i][j] = graph[i][j];
}
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
return dist;
}
public static void main(String[] args) {
int[][] graph = new int[][]{
{
0, 2, INF, 6, INF},
{
2, 0, 3, INF, INF},
{
INF, 3, 0, 4, INF},
{
6, INF, 4, 0, 8},
{
INF, INF, INF, 8, 0}
};
int[][] dist = floyd(graph);
for (int i = 0; i < dist.length; i++) {
System.out.println(Arrays.toString(dist[i]));
}
}
}
Dans cette implémentation, nous copions d'abord la matrice d'adjacence du graphe dans la matrice de distance. Ensuite, nous parcourons toutes les paires de nœuds (i,j), en essayant de raccourcir la distance entre (i,j) et le nœud k. Si la distance peut être raccourcie en passant par le nœud k, mettez à jour l'élément (i, j) dans la matrice de distance.
La complexité temporelle de cette implémentation est O(n^3), où n est le nombre de nœuds.