Question : Dans le système de coordonnées planes bidimensionnelles, pour tout polygone, les coordonnées de chaque sommet sont connues et l'aire du polygone est calculée.
Quand j'ai vu les mots "coordinates" et "area", la première chose à laquelle j'ai pensé a été le contenu du dernier blog que je viens d'écrire : le produit extérieur des vecteurs. Ensuite, nous essayons de partir du produit extérieur du vecteur pour voir si nous pouvons répondre au problème du calcul de l'aire.
Définition du produit extérieur vectoriel :
Si deux vecteurs
Alors =
Afin de faciliter le calcul et la dérivation, nous faisons encore évoluer la formule de définition du produit extérieur, comme suit :
=
=
=
Réduction de la dimensionnalité à un plan bidimensionnel, on pose , on obtient
=
=
, qui
représentent respectivement les vecteurs unitaires des axes x, y et z.
Parce que dans la troisième colonne, à l'exception de la première ligne, toutes les autres lignes sont 0, nous développons donc en fonction de la troisième colonne du déterminant et obtenons
=
=
=
, qui
représente
le cofacteur algébrique.
Ainsi, lorsque nous calculons le produit extérieur de deux vecteurs dans un plan bidimensionnel, nous pouvons l'évaluer en calculant le déterminant du tableau ordonné des coordonnées des deux vecteurs. Dans le blog précédent, nous avons vérifié que la valeur absolue du produit extérieur de deux vecteurs est égale à deux fois l'aire du triangle délimité par l'origine et les trois points.
Avec cette fondation en place, revenons à la question.
Le problème décrit un polygone. Commençons par le polygone le plus simple : un triangle, comme le montre la figure ci-dessous :
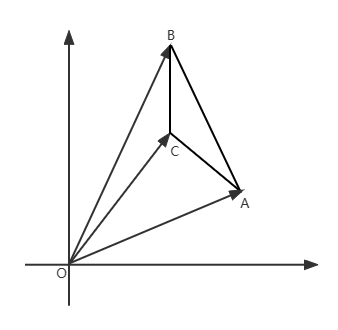
L'aire du triangle dans la figure ci-dessus est égale à
Nous utilisons le produit extérieur vectoriel pour amener l'aire de chaque triangle dans la formule ci-dessus, nous pouvons obtenir
=
Remarque : lorsque les vecteurs sont multipliés par croisement, le résultat sera positif ou négatif, et le positif et le négatif représentent la direction qui satisfait la règle de la main droite.
Après avoir calculé les triangles, nous passons aux quadrilatères.
Le quadrilatère devient un peu plus compliqué, car le quadrilatère a des côtés dits convexes et concaves Essayons de voir si les deux scénarios peuvent avoir la même idée de calcul, c'est-à-dire pas de sensation de bosses. Nous calculons d'abord les deux graphiques séparément.
Forme convexe :
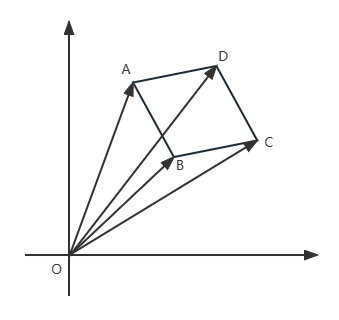
=
=
Forme concave :
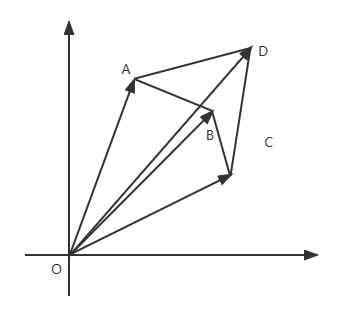
=
=
On constate que les formules des résultats supérieur et inférieur sont unifiées, c'est-à-dire les côtés convexe et concave du quadrilatère.Lorsque vous utilisez le produit extérieur vectoriel pour le calcul de l'aire, la formule de calcul est cohérente et il n'y a aucune sensation de bosses .
Maintenant, nous avons vérifié une méthode de résolution de problèmes des triangles aux quadrilatères, qui est :
Les vecteurs composés de chaque sommet et de l'origine du polygone, dans le sens inverse des aiguilles d'une montre (ou dans le sens des aiguilles d'une montre, peuvent également être utilisés), et les deux vecteurs avant et après sont multipliés pour trouver le produit extérieur, et les vecteurs de queue et de tête sont également multipliés de manière croisée (en d'autres termes, c'est-à-dire que les deux extrémités connectées par chaque arête du graphique doivent être multipliées de manière croisée par tête-à-queue ), puis la valeur absolue de la moitié de la somme obtenue en ajoutant tous les produits extérieurs sont l'aire du polygone. Tout de suite
=
Cette méthode de calcul peut-elle être appliquée à tous les polygones ? Prouvons-le par induction mathématique.
En supposant que lorsqu'il y a n côtés, =
est vrai, alors ajoutez un point sur cette base à ce moment
pour devenir n + 1 côtés
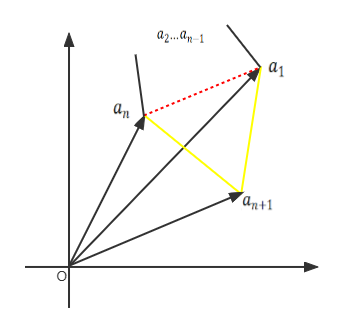
Comme le montre la figure ci-dessus, nous devons ajouter deux arêtes (la partie jaune sur la figure) et supprimer
cette arête (la ligne pointillée rouge sur la figure), puis
= +
= +
(Remarque : cela correspond à ajouter deux côtés et à supprimer un côté)
=
Le résultat final satisfait aux règles de calcul que nous avons résumées ci-dessus. Jusqu'à présent, nous avons théoriquement obtenu la solution de l'aire du polygone.
Ensuite, ensuite, nous devons transplanter cette méthode de calcul sur l'ordinateur et laisser l'ordinateur effectuer le calcul pour nous, nous devons donc continuer à faire évoluer la formule de calcul dans une forme qui convient à l'ordinateur pour calculer.
=
=
=
=
Parmi eux, à cette époque ,
c'est-à-dire
Enfin, nous avons obtenu la formule ci-dessus, qui est le célèbre théorème des lacets Shoelace Theorem .
Quelles sont ses caractéristiques ? Empruntons des images à Internet, comme suit:
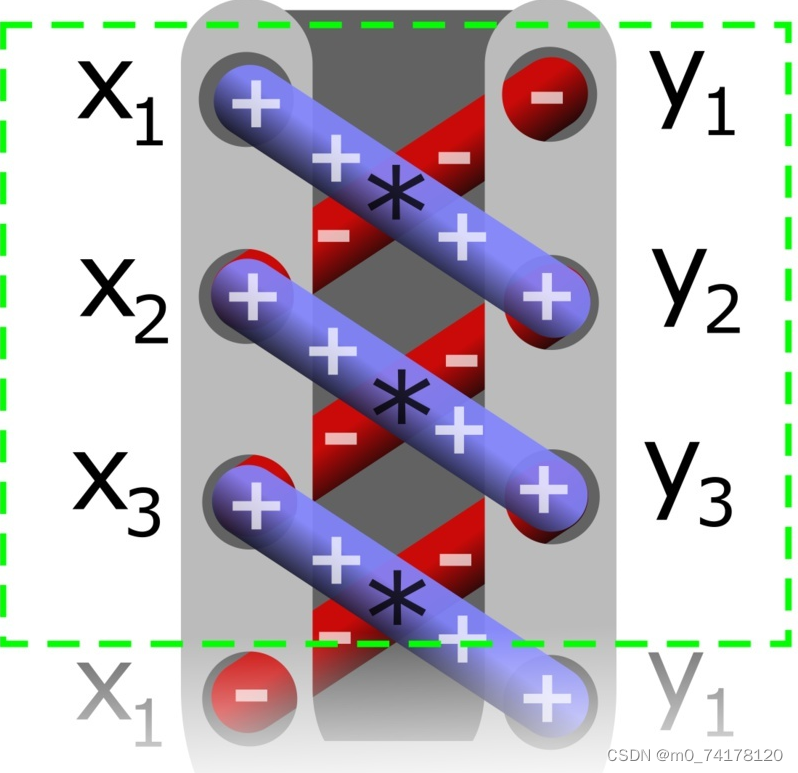
Parce que cette formule fonctionne comme un lacet, on l'appelle le théorème du lacet.
Avec le théorème du lacet, nous pouvons facilement le porter dans le code.
struct Point2d
{
double x;
double y;
Point2d(double xx, double yy): x(xx), y(yy){}
};
//计算任意多边形的面积,顶点按照顺时针或者逆时针方向排列
double ComputePolygonArea(const vector<Point2d> &points)
{
int point_num = points.size();
if(point_num < 3)return 0.0;
double s = 0;
for(int i = 0; i < point_num; ++i)
s += points[i].x * points[(i+1)%point_num].y - points[i].y * points[(i+1)%point_num].x;
return fabs(s/2.0);
}