Les modèles de transformateurs sont à la base des systèmes d'IA. Il existe déjà d'innombrables diagrammes de la structure de base de "comment Transformer fonctionne".
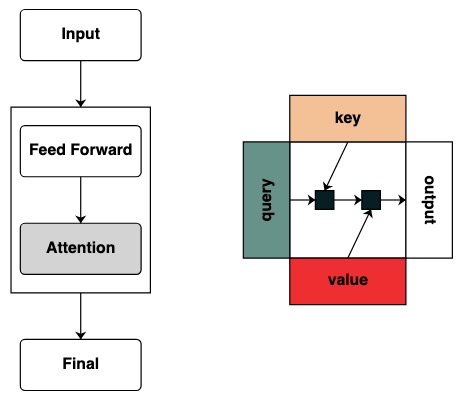
Mais ces diagrammes ne fournissent aucune représentation intuitive du cadre de calcul de ce modèle. Lorsqu'un chercheur s'intéresse au fonctionnement d'un transformateur, il devient très utile d'avoir une intuition sur son fonctionnement.
Dans l'article Thinking Like Transformers , un cadre informatique de la classe Transformer est proposé, qui calcule et imite directement les calculs Transformer. En utilisant le langage de programmation RASP , chaque programme est compilé dans un transformateur spécial.
Dans cet article de blog, j'ai reproduit une variante de RASP (RASPy) en Python. La langue est à peu près la même que l'original, mais avec quelques modifications supplémentaires que je trouve intéressantes. Avec ces langages, le travail de l'auteur Gail Weiss offre un ensemble stimulant de moyens intéressants et corrects pour aider à comprendre leur fonctionnement.
!pip install git+https://github.com/srush/RASPy
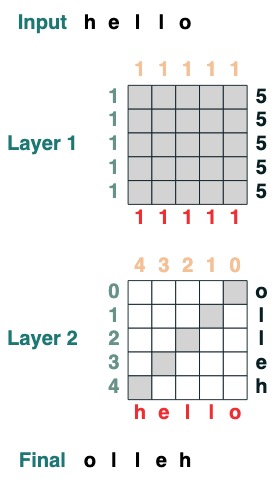
Avant de parler du langage lui-même, regardons un exemple de ce à quoi ressemble le codage avec Transformers. Voici un code qui calcule un retournement, c'est-à-dire inverse la séquence d'entrée. Le code lui-même utilise deux couches Transformer pour appliquer l'attention et des calculs mathématiques pour arriver à ce résultat.
def flip():
length = (key(1) == query(1)).value(1)
flip = (key(length - indices - 1) == query(indices)).value(tokens)
return flip
flip()
Annuaire d'articles
- Partie 1 : Transformers as code
- Partie II : Écrire des programmes avec des transformateurs
Transformateurs en tant que code
Notre objectif est de définir un ensemble de formes de calcul qui minimisent la représentation des transformateurs. Nous décrirons chaque construction de langage et sa contrepartie dans Transformers par analogie. (Pour la spécification de la langue officielle, veuillez consulter le lien vers le texte intégral du document au bas de cet article).
L'unité de base du langage est l'opération de séquence qui transforme une séquence en une autre séquence de même longueur. Je les appellerai transformations plus tard.
entrer
Dans un Transformer, la couche de base est une entrée en aval d'un modèle. Cette entrée contient généralement des informations brutes sur le jeton et l'emplacement.
Dans le code, les caractéristiques des jetons représentent la transformation la plus simple, qui renvoie les jetons après le modèle, et la séquence d'entrée par défaut est "hello":
tokens

Si nous voulons changer l'entrée dans la transformation, nous utilisons la méthode d'entrée pour transmettre la valeur.
tokens.input([5, 2, 4, 5, 2, 2])

En tant que Transformers, nous ne pouvons pas accepter directement les positions de ces séquences. Mais pour simuler les plongements de localisation, nous pouvons obtenir l'index de la localisation :
indices

sop = indices
sop.input("goodbye")

réseau d'anticipation
Après avoir traversé la couche d'entrée, nous atteignons la couche réseau feedforward. Dans Transformer, cette étape applique des opérations mathématiques indépendamment à chaque élément de la séquence.
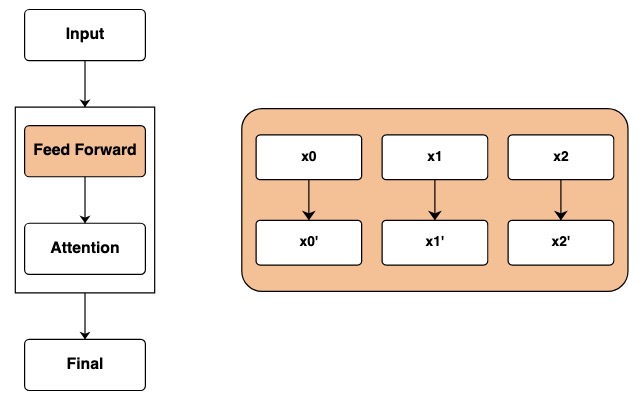
Dans le code, nous représentons cette étape en calculant sur les transformées. Des opérations mathématiques indépendantes sont effectuées sur chaque élément de la séquence.
tokens == "l"

Le résultat est une nouvelle transformée qui est calculée comme refactorisée une fois la nouvelle entrée reconstruite :
model = tokens * 2 - 1
model.input([1, 2, 3, 5, 2])

Cette opération peut combiner plusieurs transformations. Par exemple, prenez le jeton et les indices mentionnés ci-dessus comme exemple, ici vous pouvez classer Transformer pour suivre plusieurs informations :
model = tokens - 5 + indices
model.input([1, 2, 3, 5, 2])

(tokens == "l") | (indices == 1)

Nous fournissons quelques fonctions d'assistance pour faciliter l'écriture des transformations, par exemple, wherepour fournir une structure avec ifdes fonctionnalités .
where((tokens == "h") | (tokens == "l"), tokens, "q")

mapNous permet de définir nos propres opérations, telles que intla conversion . (Les utilisateurs doivent être prudents avec les opérations calculées par des réseaux de neurones simples qui peuvent être utilisés)
atoi = tokens.map(lambda x: ord(x) - ord('0'))
atoi.input("31234")

Les fonctions (fonctions) peuvent facilement décrire la cascade de ces transformations. Par exemple, voici l'opération où et atoi sont appliqués et 2 est ajouté
def atoi(seq=tokens):
return seq.map(lambda x: ord(x) - ord('0'))
op = (atoi(where(tokens == "-", "0", tokens)) + 2)
op.input("02-13")

filtre d'attention
Les choses commencent à devenir intéressantes lorsque vous commencez à appliquer le mécanisme de l'attention. Cela permettra l'échange d'informations entre les différents éléments de la séquence.
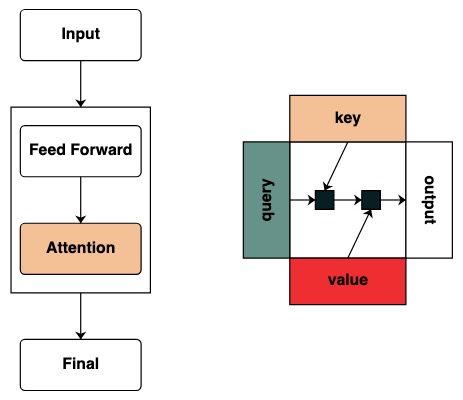
Nous commençons à définir le concept de clé et de requête, les clés et les requêtes peuvent être créées directement à partir des transformations ci-dessus. Par exemple, si nous voulons définir une clé, nous l'appelons key.
key(tokens)

querypareil pour
query(tokens)

Les scalaires peuvent keyêtre queryutilisés comme ou , et ils diffusent sur la longueur de la séquence sous-jacente.
query(1)

Nous créons des filtres pour appliquer des opérations entre la clé et la requête. Cela correspond à une matrice binaire indiquant sur quelle clé chaque requête est concernée. Contrairement aux transformateurs, aucun poids n'est ajouté à cette matrice d'attention.
eq = (key(tokens) == query(tokens))
eq
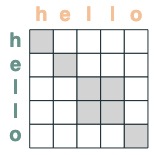
Quelques exemples:
- La position de correspondance du sélecteur est décalée de 1 :
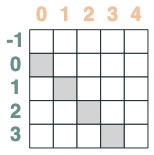
offset = (key(indices) == query(indices - 1))
offset
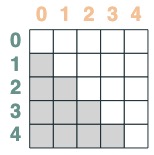
- Un sélecteur dont la clé est antérieure à la requête :
before = key(indices) < query(indices)
before
- Un sélecteur dont la clé est postérieure à la requête :
after = key(indices) > query(indices)
after
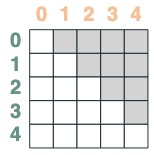
Les sélecteurs peuvent être combinés via des opérations booléennes. Par exemple, ce sélecteur combine before et eq, et nous le montrons en incluant une paire clé/valeur dans la matrice.
before & eq
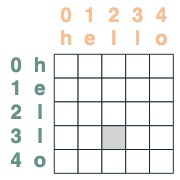
utiliser le mécanisme de l'attention
Étant donné un sélecteur d'attention, nous pouvons fournir une séquence de valeurs pour l'agrégation. On agrège en accumulant les valeurs de vérité sélectionnées par ces sélecteurs.
(Remarque : dans l'article d'origine, ils utilisent une opération d'agrégation moyenne et montrent une structure intelligente dans laquelle l'agrégation moyenne peut représenter le calcul de la somme. RASPy utilise l'accumulation par défaut pour le garder simple et éviter la fragmentation. En fait, cela signifie que raspy peut sous-estimer le nombre de couches nécessaires. Les modèles basés sur la moyenne peuvent nécessiter le double de ce nombre de couches)
Notez que les opérations d'agrégation nous permettent de calculer des caractéristiques comme des histogrammes.
(key(tokens) == query(tokens)).value(1)
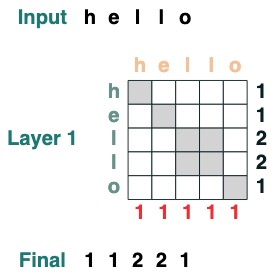
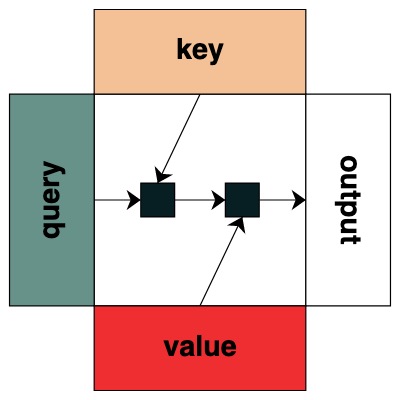
Visuellement, nous suivons la structure du graphique avec la requête à gauche, la clé en haut, la valeur en bas et la sortie à droite
Certaines opérations du mécanisme d'attention ne nécessitent même pas de jeton d'entrée. Par exemple, pour calculer la longueur de la séquence, nous créons un filtre d'attention "tout sélectionner" et lui attribuons une valeur.
length = (key(1) == query(1)).value(1)
length = length.name("length")
length
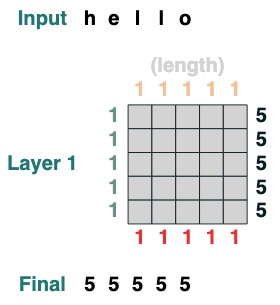
Voici des exemples plus complexes, présentés étape par étape ci-dessous. (C'est un peu comme faire une interview)
On veut calculer la somme des valeurs adjacentes d'une séquence, d'abord on tronque vers l'avant :
WINDOW=3
s1 = (key(indices) >= query(indices - WINDOW + 1))
s1
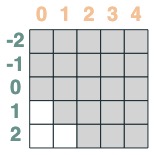
Puis on tronque vers l'arrière :
s2 = (key(indices) <= query(indices))
s2
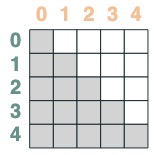
Les deux se croisent :
sel = s1 & s2
sel
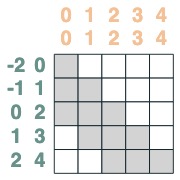
Agrégation finale :
sum2 = sel.value(tokens)
sum2.input([1,3,2,2,2])
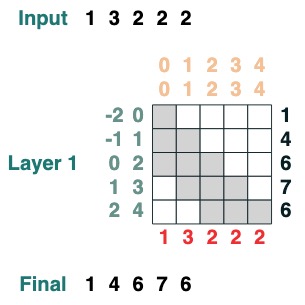
Voici un exemple qui permet de calculer la somme cumulée. Ici, nous introduisons la possibilité de nommer la transformation pour vous aider à déboguer.
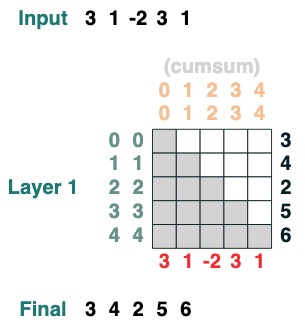
def cumsum(seq=tokens):
x = (before | (key(indices) == query(indices))).value(seq)
return x.name("cumsum")
cumsum().input([3, 1, -2, 3, 1])
couche
Le langage prend en charge la compilation de transformations plus complexes. Il calcule également les couches en gardant une trace de chaque opération.
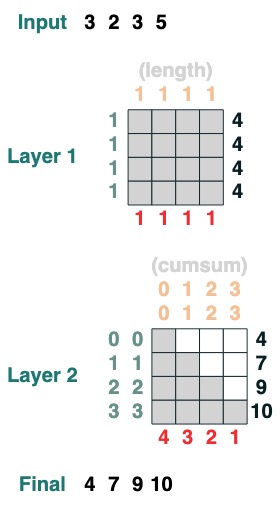
Voici un exemple de transformée à 2 couches, la première correspondant au calcul de la longueur et la seconde correspondant à la somme cumulée.
x = cumsum(length - indices)
x.input([3, 2, 3, 5])
Programmation avec transformateurs
En utilisant cette bibliothèque, nous pouvons écrire une tâche complexe. Gail Weiss m'a posé une question extrêmement difficile pour décomposer cette étape : Pouvons-nous charger un transformateur qui ajoute des nombres de n'importe quelle longueur ?
Par exemple : étant donné une chaîne "19492+23919", pouvons-nous charger la sortie correcte ?
Si vous voulez l'essayer vous-même, nous fournissons une version vous pouvez essayer vous-même.
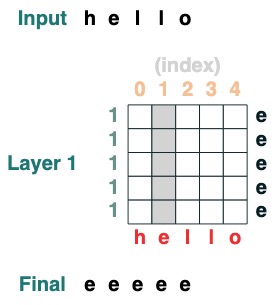
Défi 1 : Choisir un index donné
charge une séquence avec tous les éléments ià
def index(i, seq=tokens):
x = (key(indices) == query(i)).value(seq)
return x.name("index")
index(1)
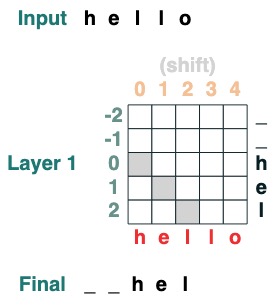
Deuxième défi : Conversion
Déplacez tous les jetons vers la droite par iposition .
def shift(i=1, default="_", seq=tokens):
x = (key(indices) == query(indices-i)).value(seq, default)
return x.name("shift")
shift(2)
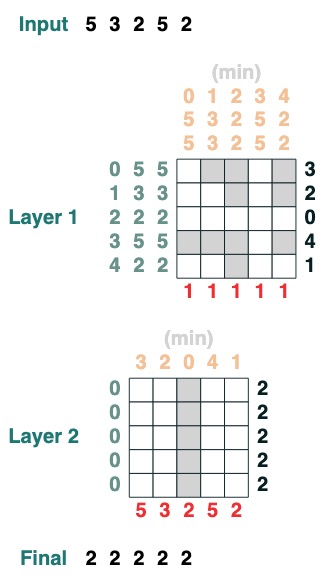
Défi 3 : Minimiser
Calcule la valeur minimale d'une séquence. (Cette étape devient difficile, notre version utilise un mécanisme d'attention à 2 couches)
def minimum(seq=tokens):
sel1 = before & (key(seq) == query(seq))
sel2 = key(seq) < query(seq)
less = (sel1 | sel2).value(1)
x = (key(less) == query(0)).value(seq)
return x.name("min")
minimum()([5,3,2,5,2])
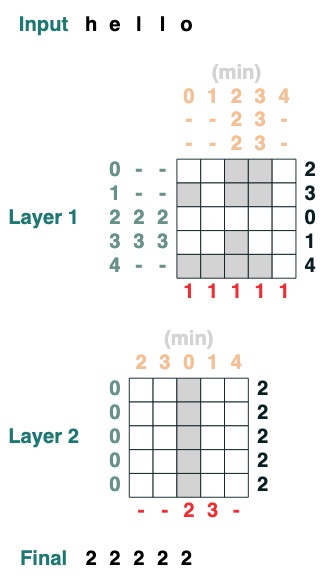
Défi quatre : premier index
Calculer le premier indice avec le jeton q (2 couches)
def first(q, seq=tokens):
return minimum(where(seq == q, indices, 99))
first("l")
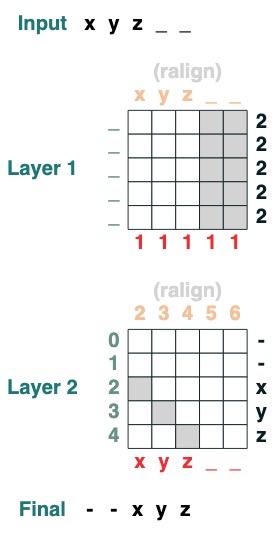
Cinquième défi : Alignement correct
Aligne à droite une séquence de remplissage. Exemple : " ralign().inputs('xyz___') ='—xyz'" (2 couches)
def ralign(default="-", sop=tokens):
c = (key(sop) == query("_")).value(1)
x = (key(indices + c) == query(indices)).value(sop, default)
return x.name("ralign")
ralign()("xyz__")
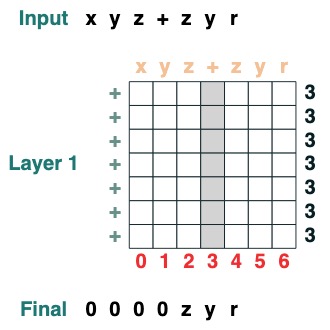
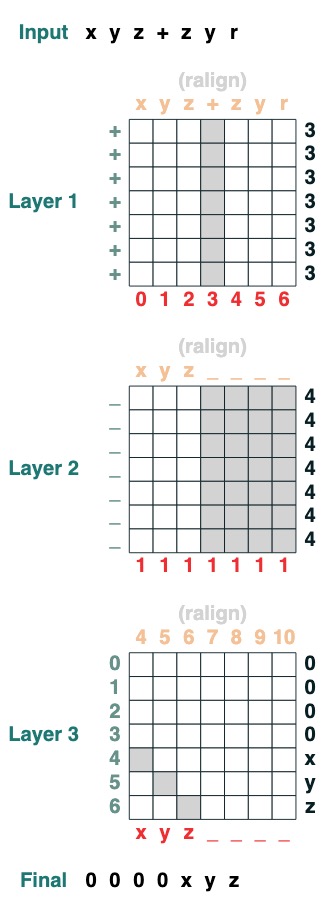
Sixième défi : Séparation
Diviser une séquence en deux parties au jeton "v" et aligner à droite (2 couches) :
def split(v, i, sop=tokens):
mid = (key(sop) == query(v)).value(indices)
if i == 0:
x = ralign("0", where(indices < mid, sop, "_"))
return x
else:
x = where(indices > mid, sop, "0")
return x
split("+", 1)("xyz+zyr")
split("+", 0)("xyz+zyr")
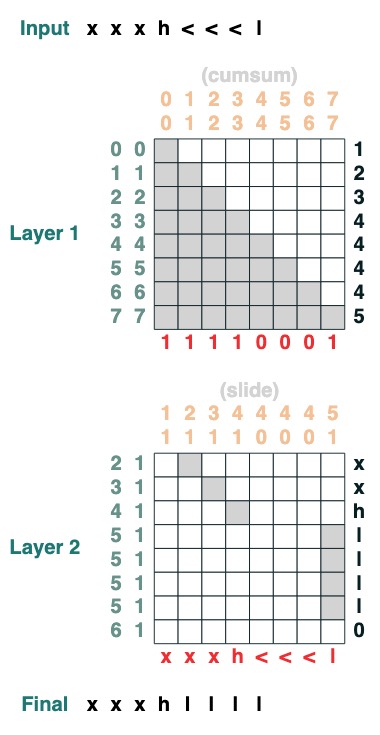
Défi 7 : Swipe
Remplacez le jeton spécial "<" par la valeur "<" la plus proche (2 niveaux) :
def slide(match, seq=tokens):
x = cumsum(match)
y = ((key(x) == query(x + 1)) & (key(match) == query(True))).value(seq)
seq = where(match, seq, y)
return seq.name("slide")
slide(tokens != "<").input("xxxh<<<l")
Huitième défi : Augmenter
Vous souhaitez effectuer l'addition de deux nombres. Voici les étapes.
add().input("683+345")
- Diviser en deux parties. Convertir en plastique. se joindre à
"683+345" => [0, 0, 0, 9, 12, 8]
- Calculez la clause de retenue. Trois possibilités : 1 porte, 0 ne porte pas, < peut-être porte.
[0, 0, 0, 9, 12, 8] => "00<100"
- Coefficient de portage coulissant
"00<100" => 001100"
- ajout complet
Ce sont 1 ligne de code. Le système complet est composé de 6 mécanismes d'attention. (Bien que Gail dise que vous pouvez le faire en 5 si vous faites assez attention !).
def add(sop=tokens):
# 0) Parse and add
x = atoi(split("+", 0, sop)) + atoi(split("+", 1, sop))
# 1) Check for carries
carry = shift(-1, "0", where(x > 9, "1", where(x == 9, "<", "0")))
# 2) In parallel, slide carries to their column
carries = atoi(slide(carry != "<", carry))
# 3) Add in carries.
return (x + carries) % 10
add()("683+345")
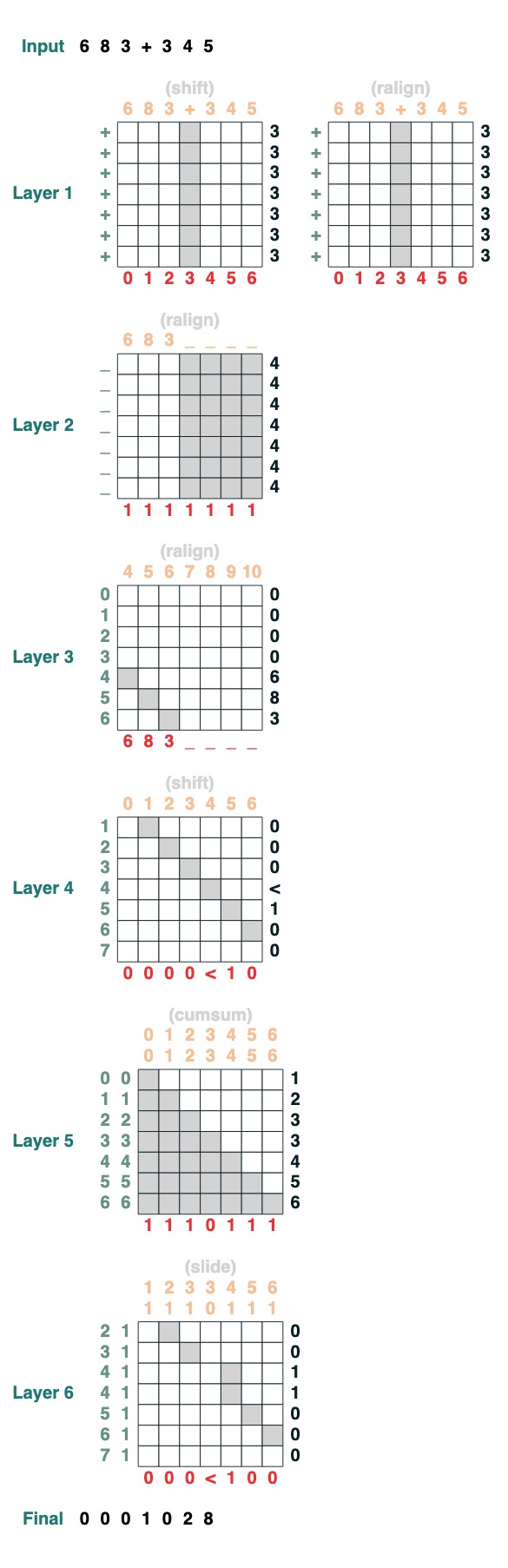
683 + 345
1028
Fait parfaitement !
Références et liens dans le texte :
- Si ce sujet vous intéresse et que vous souhaitez en savoir plus, consultez l'article : Penser comme des transformateurs
- et apprenez-en plus sur le langage RASP
- Si vous êtes intéressé par "Langages formels et réseaux de neurones" (FLaNN) ou connaissez quelqu'un qui est intéressé, n'hésitez pas à l'inviter à rejoindre notre communauté en ligne !
- Cet article de blog contient le contenu de la bibliothèque, du bloc-notes et de l'article de blog
- Ce billet de blog a été co-écrit par Sasha Rush et Gail Weiss
<h>
Texte original en anglais : Thinking Like Transformers
Traducteur : innovation64 (Li Yang)