1. Définition:
dansGraphique non dirigé connectéG(V,E)Trouvez un Esous-ensemble acyclique d' arêtes dans T, afin qu'il puisse connecter tous les nœuds et avoir le plus petit poids.
une)Puisque T est acyclique, il peut être considéré comme un arbre;
B)Puisqu'il est généré par le graphe G, il est appelé (graphe G) arbre couvrant;
C)Puisque T a le poids le plus petit, on l'appelle l'arbre couvrant minimum.
Puisque T est acyclique, les sommets V doivent avoir des arêtes V-1.
2. Stratégie gourmande:
chaque fois qu'une arête de l'arbre couvrant minimum est développée, des cycles V-1 sont exécutés pour terminer la construction de l'arbre. Les bords de croissance doivent être des bords légers (poids minimum) et ne pas former un anneau.
Méthode: algorithme de Kruskal (Kruskal) ou algorithme prim (premier)
3. Algorithme Prim (prime):
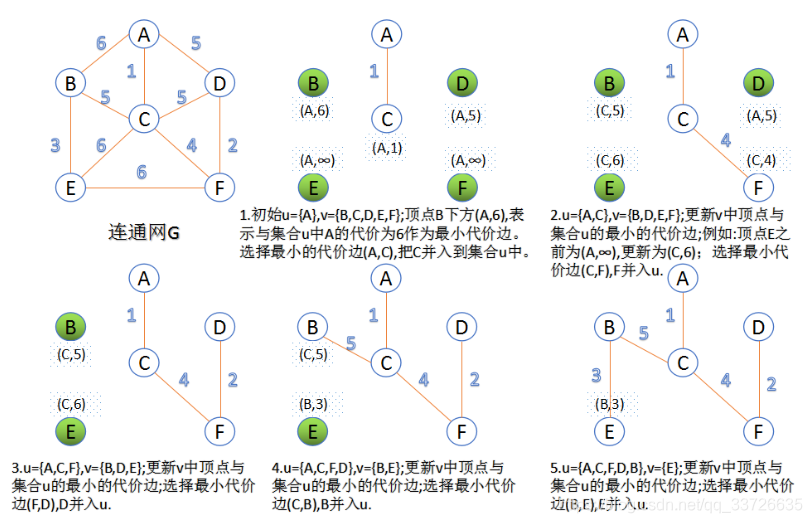
Cet algorithme peut être appelé la méthode d'addition de points . Chaque itération sélectionne le point correspondant à l'arête la moins coûteuse et l'ajoute à l'arbre couvrant minimum. L'algorithme part de n'importe quel sommet s et se développe progressivement pour couvrir tous les sommets de tout le graphe connecté.
3.1. Flux et graphique de l'algorithme:
entrée: graphique G(V,E)et tout nœud ucomme point de départ; sortie: jeu d'arêtes P
- Le nœud
urejoint la collection de nœudsU; - Sélectionnez l'
Uarête la moins coûteuse connectée aux nœuds de l' ensemble pour joindre l'ensembleP(comme les arêtes<u,v>) etvjoignez les nœuds connectés (tels que ) à l'ensembleU;
(S'il y a plusieurs arêtes avec le même poids, vous pouvez en choisir une à volonté); - Répétez l'étape 2 jusqu'à ce que tous les nœuds rejoignent l'ensemble
U.
3.2. Code C ++:
#include <queue>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct edge {
// 边的定义
int start;
int end;
int weight;
edge(int x, int y, int z) :start(x), end(y), weight(z) {
}
bool operator< (const edge& tmp) const {
//用于优先队列的比较函数
return weight > tmp.weight;
}
};
const int NUM = 6;
int G[NUM][NUM]; //假设图已经定义好了,如G[0][2] = 5; 5为权重
void MiniSpanTree_prim(int(*G)[NUM], int root)
{
vector<int> V; //记录MST已经包含的点;
V.push_back(root);
priority_queue<edge> edge_all; // 放入权重边,自动排序
for (int i = 0; i < NUM; i++) {
// 放入与起点连接的边
if (G[root][i] != 0) {
// 0 代表没有路
edge tmp(root, i, G[root][i]);
edge_all.push(tmp);
}
}
cout << "Prim :" << endl;
for (int i = 0; i < NUM - 1; i++) {
//共N-1条边
edge curr = edge_all.top(); //取得代价最小边
edge_all.pop();
while (find(V.begin(), V.end(), curr.end) != V.end()) {
//边终点若已包含,则丢弃后换一条边
curr = edge_all.top();
edge_all.pop();
}
V.push_back(curr.end); //放入这条边的终点v
cout << curr.start << " --> " << curr.end << " " << curr.weight << endl; // 输出MST的边
for (int j = 0; j < NUM; j++) {
// 加入终点v连接的边
if (G[curr.end][j] != 0 && find(V.begin(), V.end(), j) == V.end()) {
edge tmp(curr.end, j, G[curr.end][j]);
edge_all.push(tmp);
}
}
}
}
4. Algorithme de Kruskal (Kruskal):
Cet algorithme peut être appelé la méthode de l'arête additive , le numéro d'arête de l'arbre couvrant minimum initial est 0, et chaque itération sélectionne une arête de coût minimum qui répond à la condition et l'ajoute à l'ensemble d'arêtes de l'arbre couvrant minimum. dans.
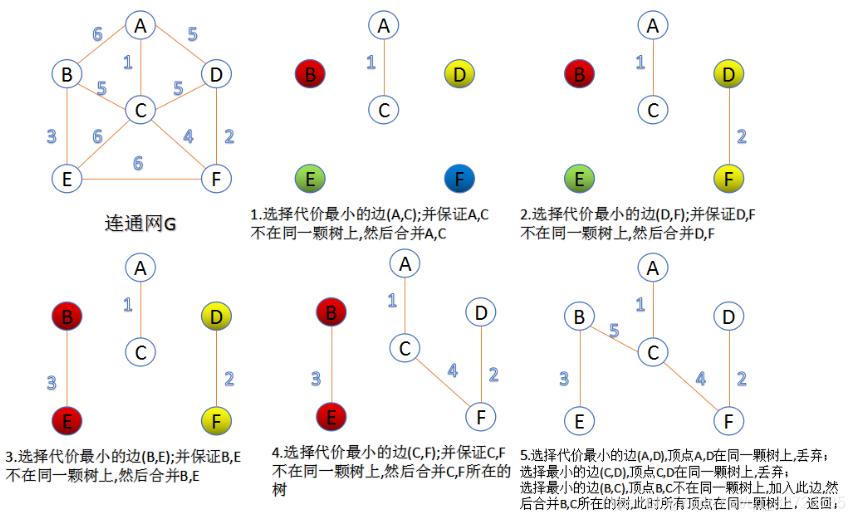
4.1. Flux et diagramme de l'algorithme:
entrée: graphique G(V,E); sortie: jeu d'arêtes P.
- Trier toutes les arêtes du graphique du plus petit au plus grand coût;
- Considérons les n sommets du graphe comme une forêt de n arbres indépendants;
- Sélectionnez les arêtes du plus petit au plus grand poids,
u,vSi les deux sommets de l'arête sélectionnée appartiennent à deux arbres différents, ils deviennent une arête de l'arbre couvrant minimum et les deux arbres sont fusionnés en un seul arbre en même temps. Sinon, prenez le bord avec le plus petit poids et réessayez. - Répétez (3) jusqu'à ce que tous les sommets soient dans un arbre ou qu'il y ait n-1 arêtes.
4.2. Code C ++:
#include <queue>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct edge {
// 边的定义
int start;
int end;
int weight;
edge(int x, int y, int z) :start(x), end(y), weight(z) {
}
bool operator< (const edge& tmp) const {
//用于优先队列的比较函数
return weight > tmp.weight;
}
};
const int NUM = 6;
int G[NUM][NUM]; //假设图已经定义好了,如G[0][2] = 5; 5为权重
void MiniSpanTree_kruskal(int(*G)[NUM])
{
int node_coll[NUM] = {
0 }; //判断节点是否属于一棵树
int count = 1; // 用于不同树的标记
priority_queue<edge> edge_all; // 放入权重边,自动排序
for (int i = 0; i<NUM; i++) {
//放入所有边,并自动排序
for (int j = 0; j<NUM; j++) {
if (G[i][j] != 0) {
edge tmp(i, j, G[i][j]);
edge_all.push(tmp);
}
}
}
for (int i = 0; i<NUM - 1; i++) {
//共N-1条边
edge tmp = edge_all.top(); // 取代价最小边
edge_all.pop();
while (node_coll[tmp.start] == node_coll[tmp.end] && node_coll[tmp.start] != 0 && node_coll[tmp.end] != 0) {
// 找到属于不同树的边
tmp = edge_all.top();
edge_all.pop();
}
cout << tmp.start << " --> " << tmp.end << " " << tmp.weight << endl; // 输出MST的边
if (node_coll[tmp.start] == 0 && node_coll[tmp.end] == 0) {
//不同树的边的情况1
node_coll[tmp.start] = count;
node_coll[tmp.end] = count;
count++;
}
else if (node_coll[tmp.start] == 0 && node_coll[tmp.end] != 0) {
//不同树的边的情况2
node_coll[tmp.start] = count;
node_coll[tmp.start] = node_coll[tmp.end];
}
else if (node_coll[tmp.start] != 0 && node_coll[tmp.end] == 0) {
//不同树的边的情况3
node_coll[tmp.start] = count;
node_coll[tmp.end] = node_coll[tmp.start];
}
else if (node_coll[tmp.start] != 0 && node_coll[tmp.end] != 0) {
//不同树的边的情况4
node_coll[tmp.start] = count;
for (int i = 0; i<NUM; i++) {
if (node_coll[i] = node_coll[tmp.end]) {
node_coll[i] = node_coll[tmp.start];
}
}
}
}
}
Matériel de référence: Deux méthodes d'arbre couvrant minimum (algorithme Kruskal et algorithme Prim)
Introduction à l'algorithme 23.2 Algorithme Kruskal et algorithme Prim
Pour résumer:
1. L'algorithme kruskal est la méthode d'addition, l'algorithme prim est la méthode d'addition et l'idée de l'algorithme de mémoire est bonne.