Compréhension de l'algorithme de Bresenham

Bresenham

Avertissement: L'auteur de ce blog est le même que ce blog https://blog.csdn.net/cjw_soledad/article/details/78886117, car la fonction "Suppression de blog" n'est pas efficace et doit être republiée

L'algorithme de bresenham est un algorithme conçu pour la caractéristique de "l'affichage (écran ou imprimante) est composé de pixels" en infographie, de sorte que tous les points dans le processus de recherche de lignes droites sont calculés avec des nombres entiers, améliorant ainsi considérablement la vitesse de calcul .

Code d'implémentation

Cet article explique principalement le code suivant. Si vous pouvez comprendre le code suivant, vous pouvez ignorer cet article.

// 来源:https://rosettacode.org/wiki/Bitmap/Bresenham%27s_line_algorithm#C

void line(int x0, int y0, int x1, int y1) {
 
  int dx = abs(x1-x0), sx = x0<x1 ? 1 : -1;
  int dy = abs(y1-y0), sy = y0<y1 ? 1 : -1; 
  int err = (dx>dy ? dx : -dy)/2, e2;
 
  for(;;){
    setPixel(x0,y0);
    if (x0==x1 && y0==y1) break;
    e2 = err;
    if (e2 >-dx) { err -= dy; x0 += sx; }
    if (e2 < dy) { err += dx; y0 += sy; }
  }
}

Équation en ligne droite

Comme nous le savons tous, l'équation en ligne droite la plus élémentaire avec l'ordonnée à l'origine de pente est \ (y = kx + b (k est la pente, b est l'ordonnée à l'origine) \) . L'inconvénient de cette équation est qu'elle ne peut pas représenter la droite \ (x = \ alpha \) , donc une nouvelle équation est utilisée à la place de \ (Ax + By + C = 0 \) .

Bresenham

L'étape principale de l'algorithme de Bresenham pour tracer des lignes droites consiste à déterminer la position du point suivant. Il y a une image dans Wikipedia pour comparer l'image

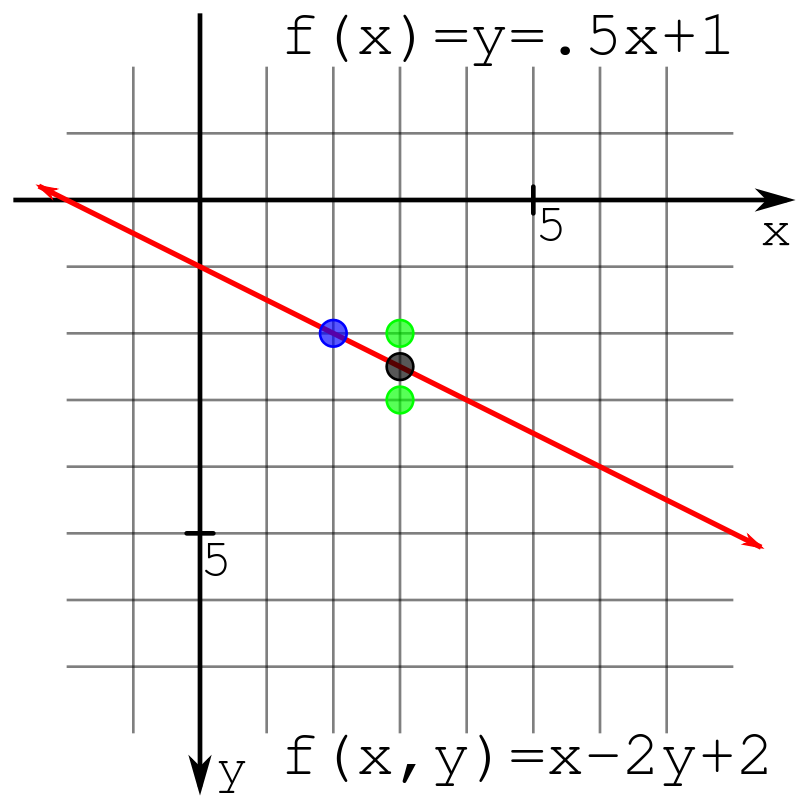
. Dans l'image, chaque point représente un pixel . Supposons que nous ayons une ligne droite \ (f (x, y) \) et la coordonnée actuelle est \ ((x, y) \) . Les étapes de la coordonnée de l'axe y d'un point sont (similaires si vous voulez déterminer la coordonnée de l'axe x):

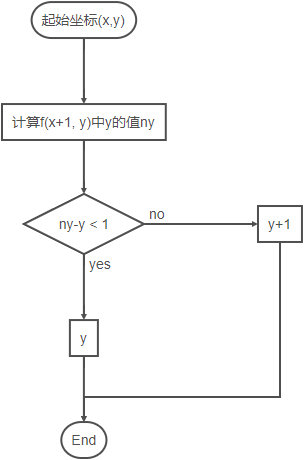
Compréhension du code

Comme mentionné ci-dessus, nous pouvons maintenant déterminer que le pixel suivant de la ligne est là, mais les avantages de l'algorithme de Bresenham ne se sont pas encore manifestés: nous devons encore calculer les nombres à virgule flottante. Afin d'éviter les calculs en virgule flottante, nous devons découvrir la règle du soulignement plus profondément.

Ici, nous ne considérons que le cas de \ (x_1 <x_2 \) et \ (y_1 <y_2 \) , en fait, nous avons seulement besoin de considérer cette situation, comme écrit dans le code précédent sx, sy, à travers ces deux variables, nous pouvons contrôler la La direction de la ligne tracée est correcte.

• L'entrée de Bresenham est de deux points \ ((x_1, y_1), (x_2, y_2) \) . Sur la base de ces deux points, nous pouvons calculer la "distance" entre les deux points. La distance ici est une valeur absolue, correspondant au code dx, dy.

\ [\ Delta x = | x_1-x_2 | \\ \ Delta y = | y_1-y_2 | \]

Selon la forme tronquée \ (y = kx + b \) , nous avons \ (y = \ frac {\ Delta y} {\ Delta x} x + b \) , puis

\ [\ Delta y x- \ Delta x y + C = 0 \]

Dans cette formule:

\ [x + 1 \ Rightarrow y + \ frac {\ Delta y} {\ Delta x} \\ y + 1 \ Rightarrow x + \ frac {\ Delta x} {\ Delta y} \]

• En fait, \ (\ frac {\ Delta y} {\ Delta x} \) et \ (\ frac {\ Delta x} {\ Delta y} \) sont utilisés pour juger de la position du point suivant . L'objectif fondamental de ces deux changements de valeur est de rendre l'équation ci-dessus vraie. Selon cela, nous introduisons directement une variable \ (err \) pour éviter l'arithmétique à virgule flottante (correspondant à la errsomme dans le code e2)

\ [\ Delta y x- \ Delta x y + C + err = 0 \\ x + 1 \ Rightarrow err- \ Delta y \\ y + 1 \ Rightarrow err + \ Delta x \]

• Maintenant , nous avons pu \ (err \) et \ (x, y \) lien, mais il est est pas résolu une question très importante: pour déterminer les augmentations ou augmenter l'axe des x coordonnées y coordonnons
  première hypothèse que nous commençons à coordonnées \ ((x, y) \) , le \ (err \) actuel est également correct, maintenant nous devons juger les coordonnées du point suivant.
  Selon l'algorithme traditionnel de Bresenham:

\ [(x + \ frac {\ Delta x} {\ Delta y}) - (x + 1)> 0 \ Rightarrow \ Delta x- \ Delta y> 0 \ Rightarrow x + 1 \\ (y + \ frac {\ Delta y} {\ Delta x}) - (y + 1)> 0 \ Rightarrow \ Delta y- \ Delta x> 0 \ Rightarrow y + 1 \]

Nous prêtons plus d'attention à la partie médiane, et la transformons avec la relation de \ (err \) et \ (\ Delta x, \ Delta y \) mentionnée au point précédent.

\ [\ Delta x- \ Delta y> 0 \ Rightarrow - \ Delta y> - \ Delta x \\ \ Delta y- \ Delta x> 0 \ Rightarrow + \ Delta x <\ Delta y \]

• D'après la formule ci-dessus, il semble que cela ait quelque chose à voir avec \ (err \) , mais ce n'est pas clair, c'est parce que notre poussée est basée sur le point de départ, si la base n'est pas le point de départ, alors la formule doit être

\ [\ Delta x- \ Delta y> 0 \ Rightarrow \ varepsilon - \ Delta y> - \ Delta x \\ \ Delta y- \ Delta x> 0 \ Rightarrow \ varepsilon + \ Delta x <\ Delta y \]

\ (\ varepsilon \) est une valeur cumulée, sa source est liée à la position relative du point actuel \ ((x, y) \) et du point de départ \ ((x_0, y_0) \) , la compréhension personnelle est: à chaque fois \ ( x + 1 \) ou \ (y + 1 \) entraînera la traduction de la ligne droite d'origine. Cette traduction provoquera une erreur et cette erreur continuera de s'accumuler au fur et à mesure que le programme progresse et cette valeur cumulée correspond à \ err \)

• Nous avons maintenant la possibilité de connecter \ (err \) au programme err.
  ifCette dernière condition correspond à la formule ci-dessus, mais est errdifférente de \ (\ varepsilon \) . La différence est: elle errest déjà calculée \ (\ varepsilon- \ Delta y \) et \ (\ varepsilon + \ Delta x \) . Nous pouvons y penser de cette façon: à un certain point \ ((x, y) \) , nous avons calculé le bon \ (err \) qui peut être utilisé pour le jugement . Lorsque nous choisissons le point suivant, nous pouvons nous arrêter Le point suivant \ (err \) est calculé , ce que le code err -= dy; err += dx;implique.

if (e2 >-dx) { err -= dy; x0 += sx; }
if (e2 < dy) { err += dx; y0 += sy; }

• À propos de l' errinitialisation en 2020

Nous avons remarqué que le code a été errinitialisé. Devant notre dérivation elle donnait sur une partie: le point de départ \ ((x 1, y_1) \ ) Le \ (ERR \) . À partir de la formule \ (Ax + By + C + err = 0 \) , le point de départ de \ (err \) doit être \ (0 \) , mais le code a été initialisé avec une valeur étrange. Il semble que les deux soient contradictoires, mais errl'initialisation est en fait une autre astuce.

int err = (dx>dy ? dx : -dy)/2

En regardant l'image mentionnée plus haut, le point bleu est le point de départ. Si le jugement est fait manuellement, nous déciderons où le prochain point est basé sur l'emplacement du point noir . Lorsque \ (noir> 0,5 \) , nous choisirons le point vert ci-dessous, sinon choisissez le point vert ci-dessus.

Cependant, l' 0.5arithmétique en virgule flottante sera introduite ici . Nous avons une autre option: déplacer le point de départ \ ((x_1, y_1) \) vers le haut d'une demi-unité (ici seulement \ (\ Delta x> \ Delta y \) est considéré , le reste est le même). Comme le point de départ est décalé du premier pixel, une erreur \ (err \) est introduite . Selon la dérivation précédente de \ (err \) :

\ [x_1 + 0,5 \ Rightarrow err- \ Delta y / 2 \\ y_1 + 0,5 \ Rightarrow err + \ Delta x / 2 \]

Cela peut expliquer errle problème de la valeur initiale et cela est cohérent avec notre dérivation précédente.

• À ce stade, l'algorithme de Bresenham est compris.