【Aprendizaje en línea】 Algoritmo de aprendizaje en línea

motivación

Los problemas del entrenamiento completo incluyen un gran tamaño de muestra, un largo tiempo de entrenamiento, un gran volumen de funciones, un largo tiempo de sincronización, un entrenamiento completo todos los días, un alto costo y un efecto retardado.
Los beneficios de la capacitación incremental, la capacitación incremental es de bajo costo y efectiva

desarrollar

OGD $\flecha correcta$ FOBOS $\flecha correcta$ RDA $\flecha correcta$ FTRL $\flecha correcta$ FTML

Todo el código: https://github.com/YEN-GitHub/OnlineLearning_BasicAlgorithm

A continuación se utiliza la regresión logística como ejemplo para implementar cada tipo de aprendizaje en línea.

Regresión logística

1. La función objetivo es la entropía cruzada, $-ylog\widehat{y}-(1-y)log(1-\widehat{y})$

2. La salida prevista es $1/(1+e^{-w^{T}x})$

3. La fórmula de actualización del gradiente es $\theta _{j}=\theta _{j}-(h_{\theta }(x^{(i)})-y^{(i)})x^{_{j}^{(i) }}$

El código se muestra a continuación:

class LR(object):

    @staticmethod
    def fn(w, x):
        ''' sigmod function '''
        return 1.0 / (1.0 + np.exp(-w.dot(x)))

    @staticmethod
    def loss(y, y_hat):
        '''cross-entropy loss function'''
        return np.sum(np.nan_to_num(-y * np.log(y_hat) - (1-y)*np.log(1-y_hat)))

    @staticmethod
    def grad(y, y_hat, x):
        '''gradient function'''
        return (y_hat - y) * x

OGD

La fórmula de actualización es: $W^{(t+1)}=W^{(t)}-\eta ^{(t+1)}G^{(t)}$

El código se muestra a continuación:

class OGD(object):

    def __init__(self,alpha,decisionFunc=LR):
        self.alpha = alpha
        self.w = np.zeros(4)
        self.decisionFunc = decisionFunc

    def predict(self, x):
        return self.decisionFunc.fn(self.w, x)

    def update(self, x, y,step):
        y_hat = self.predict(x)
        g = self.decisionFunc.grad(y, y_hat, x)
        learning_rate = self.alpha / np.sqrt(step + 1)  # damping step size
        # SGD Update rule theta = theta - learning_rate * gradient
        self.w = self.w - learning_rate * g
        return self.decisionFunc.loss(y,y_hat)

TG

El método SGD no puede garantizar la escasez de soluciones, y los conjuntos de datos a gran escala y las características de alta dimensión requieren soluciones escasas. El método más intuitivo es el método de truncamiento de gradiente. Cuando el parámetro es menor que el umbral, se le asigna 0, o da un paso hacia 0, lo cual se puede hacer cada k pasos. Realizar un truncamiento

El código se muestra a continuación:

    def update(self, x, y, step):
        y_hat = self.predict(x)
        g = self.decisionFunc.grad(y, y_hat, x)

        if step % self.K == 0:

           learning_rate = self.alpha / np.sqrt(step+1) # damping step size

           temp_lambda = self.K * self.lambda_

           for i in range(4):
              w_e_g = self.w[i] -learning_rate * g[i]
              if (0< w_e_g <self.theta) :
                  self.w[i] = max(0, w_e_g - learning_rate * temp_lambda)
              elif (-self.theta< w_e_g <0) :
                  self.w[i] = min(0, w_e_g + learning_rate * temp_lambda)
              else:
                  self.w[i] = w_e_g
        else:
            # SGD Update rule theta = theta - learning_rate * gradient
            self.w = self.w - self.alpha * g

        return self.decisionFunc.loss(y,y_hat)

FOBOS

L1-fobos puede considerarse un caso especial de TG. Cuando $\theta =\infty , k=1$ L1-FOBOS es equivalente a TG, también da un paso en la dirección del gradiente y un paso en la dirección de 0 cada vez. En comparación con TG, FOBOS tiene un marco teórico de optimización y la actualización de pesos se divide en los dos pasos siguientes:

Consulte el blog para conocer el proceso de solución: https://zr9558.com/2016/01/12/forward-backward-splitting-fobos/

Obtenga la fórmula de actualización del algoritmo:

Traducido al código:

    def update(self, x, y, step):
        y_hat = self.predict(x)
        g = self.decisionFunc.grad(y, y_hat, x)
        learning_rate = self.alpha / np.sqrt(step + 1)  # damping step size
        learning_rate_p = self.alpha / np.sqrt(step + 2)  # damping step size
        for i in range(len(x)):
            w_e_g = self.w[i] - learning_rate * g[i]
            self.w[i] = np.sign(w_e_g)  *  max(0.,np.abs(w_e_g)-learning_rate_p * self.lambda_)
        return self.decisionFunc.loss(y,y_hat)

CDR

La diferencia entre L1-RDA y L1-FOBOS es que considera el valor promedio del gradiente acumulado, por lo que es más fácil generar soluciones dispersas. Para una introducción detallada al algoritmo, consulte el blog:

https://zr9558.com/2016/01/12/regularized-dual-averaging-algorithm-rda/

optimizar el objetivo:

Actualización del algoritmo:

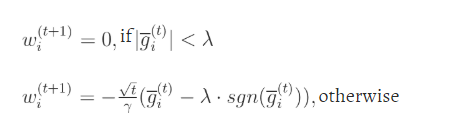
Código:

    def update(self, x, y, step):
        y_hat = self.predict(x)
        g = self.decisionFunc.grad(y, y_hat, x)
        self.g = (step-1)/step * self.g + (1/step) * g
        for i in range(len(x)):
            if (abs(self.g[i])<self.lambda_):
                self.w[i] = 0
            else:
                self.w[i] = -1* (np.sqrt(step)/self.gamma)*(self.g[i] - self.lambda_ * np.sign(self.g[i]))

        return self.decisionFunc.loss(y,y_hat)

FTRL

ftrl considera exhaustivamente los métodos de gradiente y regularización de RDA y FOBOS, teniendo en cuenta no solo todos los gradientes anteriores, sino también la regularidad L1 y la regularidad L2. Los objetivos de optimización son los siguientes:

        self.w = np.array([0 if np.abs(self.z[i]) <= self.l1
                             else (np.sign(self.z[i] * self.l1) * self.l1 - self.z[i]) / (self.l2 + (self.beta + np.sqrt(self.q[i]))/self.alpha)
                             for i in range(self.dim)])

        y_hat = self.predict(x)
        g = self.decisionFunc.grad(y, y_hat, x)
        sigma = (np.sqrt(self.q + g*g) - np.sqrt(self.q)) / self.alpha
        self.z += g - sigma * self.w
        self.q += g*g
        return self.decisionFunc.loss(y,y_hat)