[Planificación de movimiento de robot móvil] 04 - Generación de trayectoria

prefacio

Parte del contenido de este artículo se refiere a la planificación del movimiento del robot móvil de Deep Blue Academy , y toma notas y arreglos pertinentes en consecuencia.

Acabado de código relacionado:

1. https://gitee.com/lxyclara/motion-plan-homework/
2. https://github.com/KailinTong/Motion-Planning-for-Mobile-Robots/blob/master
3. https://gitee.com/aries-wu/Motion-plan/blob/main/
4. Enlace: https://pan.baidu.com/s/1UtVHRxDq771LfSGK_21wgQ?pwd=rhtp Código de extracción: rhtp

introducir

Las trayectorias experimentadas por robots y vehículos no tripulados deben satisfacer características suaves y al mismo tiempo cumplir con las restricciones dinámicas correspondientes. La ruta académica tradicional obviamente necesita generar una trayectoria optimizada después de generar el camino para ajustarse a las características de la kinodinámica; mientras que la ruta que ha sido kinodinámica necesita optimizar aún más la trayectoria para mejorar la calidad de la ruta.

La generación de trayectorias suaves generalmente debe cumplir con las siguientes características:

1. Condiciones de contorno: ubicación del punto de inicio, punto final (dirección, etc.)
2. Condiciones intermedias: posición, dirección del nodo repetidor...
3. Criterios de juicio para una trayectoria suave: la función de evaluación debe ser razonable (como $\begin{array}{r}\underset{x\to x_0^{}}{}f(x\end{array}=\begin{array}{r}\underset{x\to x_0^{}}{}f(x\end{array}$）

Optimización mínima de instantáneas

Planitud diferencial

Documento: Generación y control de trayectoria mínima de ajuste para quadrotores, Daniel Mellinger y Vijay Kumar
serán un problema de espacio de estado de dimensión completa $X$ va al espacio plano$\sigma$ para la investigación. State Space XX

para UAV Quadrotor$X$ consta de posición, dirección, velocidad lineal y velocidad angular:
$$X=[X,y,z,\varphi ,yo,pd,\dot{X},y,\dot{z},{Vaya}_{},{Vaya}_{},{Vaya}_{}{]}^{La\; velocidad\; angular\; T}$$ se observa en el propio sistema de coordenadas del UAV.

Los estados y entradas del quadrotor se pueden expresar como funciones algebraicas de las variables de salida y sus derivadas en cuatro espacios planos.
Cualquier trayectoria suave (con derivadas razonablemente acotadas) en un espacio plano puede ser rastreada por un quadrotor subactuado.

Elija 4 dimensiones como un espacio plano en el espacio de estado de 12 dimensiones: $pag=[X,y,z,\psi {]}^T$
在$T_{}\to T_{}$tiempo, la trayectoria en el espacio plano se define como: $R^3\times SO\left(2\right)$ ($R^3$ es$x,y,z,$$SO\left(2\right)$ ψ \$\psi$ )

La dinámica de un dron quadrotor se muestra a continuación, dividida en dos fórmulas:

$z_{}$Representa $eje\; z$ ,$z_{}$Representa z \mathbf{z} en el sistema de coordenadas del Cuerpo$eje\; z$ .
De la ecuación de movimiento:$$z_{}=\frac{}{\Vert t\Vert },t=[{\ddot{pag}}_{},{\ddot{pag}}_{},{\ddot{pag}}_{}+g{]}^T$$${pag}_{},{pag}_{},{pag}_{}$Para $x,y,z$ , entonces$t$ representa la dirección de la aceleración resultante del UAV. Por lo tanto, representa$z_{}$es $La\; combinación\; algebraica\; variable\; de\; \sigma$ . La actitud del dron se puede usar$X_{},y_{},z_{}$Para expresar, si $X_{},y_{},z_{}$Por combinación algebraica, entonces $\varphi ,yo,\psi$ también se puede determinar.

A continuación, defina un sistema de coordenadas intermedio $C$ , solo una diferencia de ángulo de guiñada del sistema mundial. $$X_{}=[\mathrm{porque}{pag}_{},\mathrm{pecado}{pag}_{},0{]}^T$$

用$X_{}$también $z_{}$también $y_{}$
$$y_{}=\frac{z_{}\times X_{}}{\Vert z{\_}_{}\times X_{}\Vert },X_{}=y_{}\times z_{}{R}_{}=\left[\begin{array}{ccc}{X}_{}& y_{}& z_{}\end{array}\right]$$

En este punto, solo queda la velocidad angular.
Para $metropag=-metrogramo{z}_{}+{tu}_{}{z}_{}$求导，得$metro\dot{a}={\dot{tu}}_{}{z}_{}+\left({ay}_B\right)\times {tu}_{}{z}_{}$(Esto implica cierto conocimiento de la cinemática de cuerpos rígidos) $BW$ :Velocidad angular del cuerpo
vista en el marco mundial
Debido a que el dron solo se empuja en la dirección vertical, entonces${\dot{tu}}_{}=z_{}\cdot metro\stackrel{\dot{}Define}{a}$
a$h_{}$, $h_{}={Vaya}_B\times z_{}=\frac{}{{tu}_{}}(\dot{a}-(z_{}\cdot \dot{a}\left)z_{}\right)$。$h_{}$Las cantidades en se pueden expresar en espacio plano.
Sabemos que ${Vaya}_B={Vaya}_{}{X}_{}+{Vaya}_{}{y}_{}+{Vaya}_{}{z}_{}$
沿$y_{}$、$X_{}$Da la siguiente solución: ${Vaya}_{}=-h_{}\cdot y_{},{Vaya}_{}=h_{}\cdot X_{}$

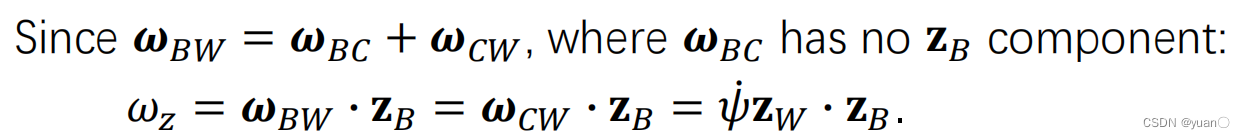
Resumen

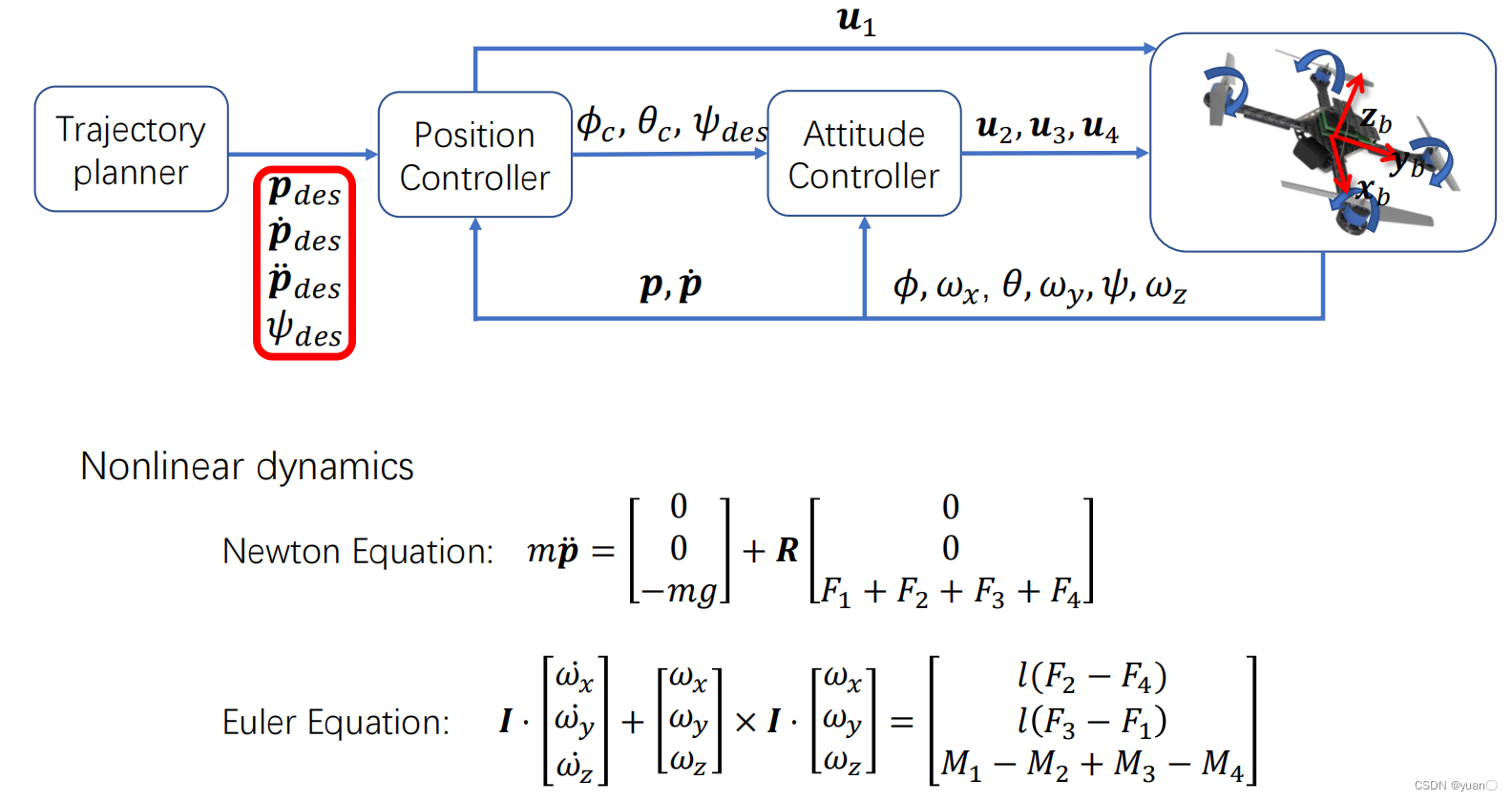
La trayectoria generada es un polinomio, que tiene las siguientes ventajas:
• Fácil determinación de los criterios de suavidad utilizando el orden polinomial
• Cálculo simple de forma cerrada de derivadas
• Generación de trayectorias tridimensionales desacopladas

complemento mínimo

Trayectoria 1D suave

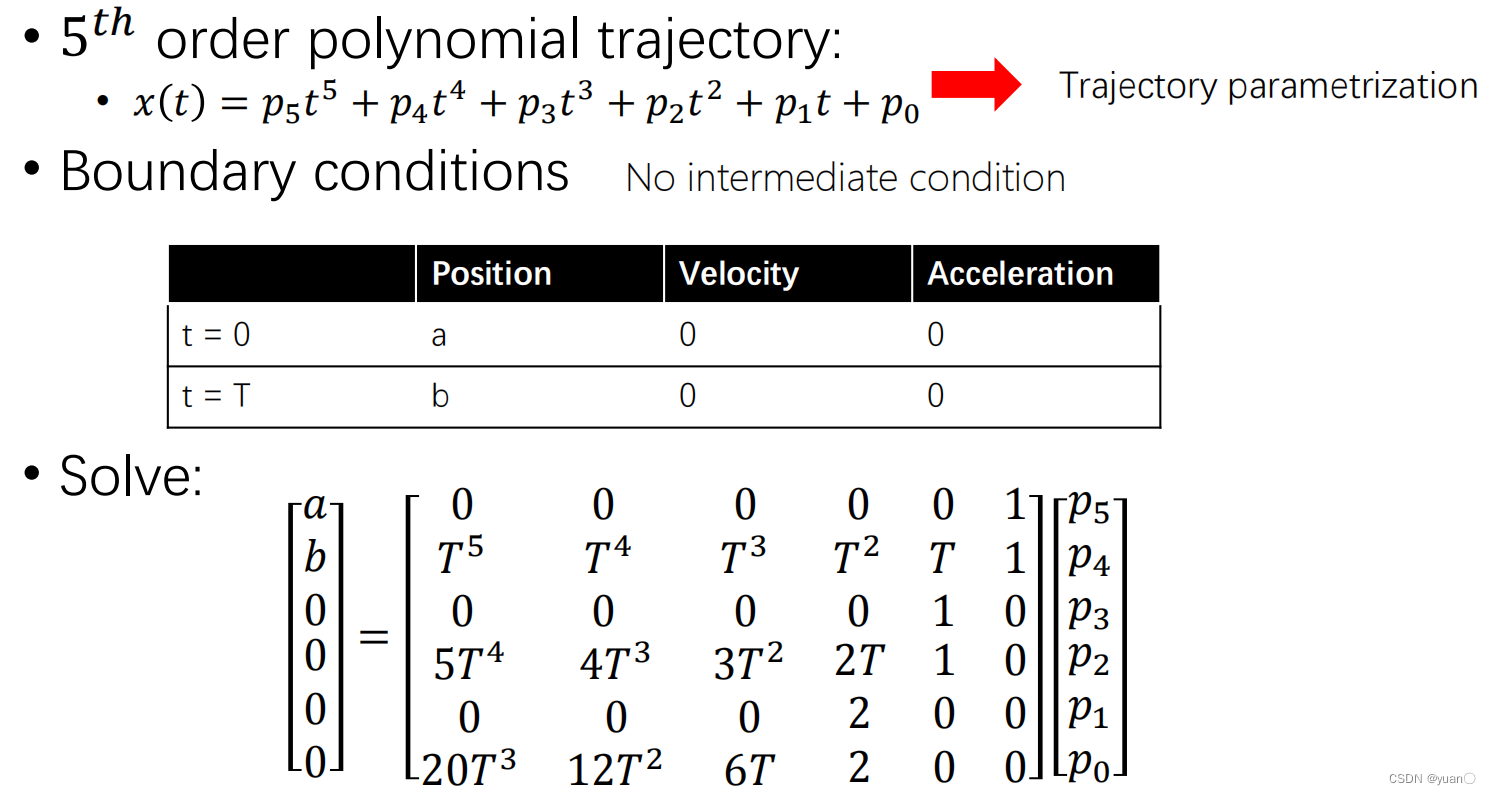
Trayectoria suave de varios segmentos

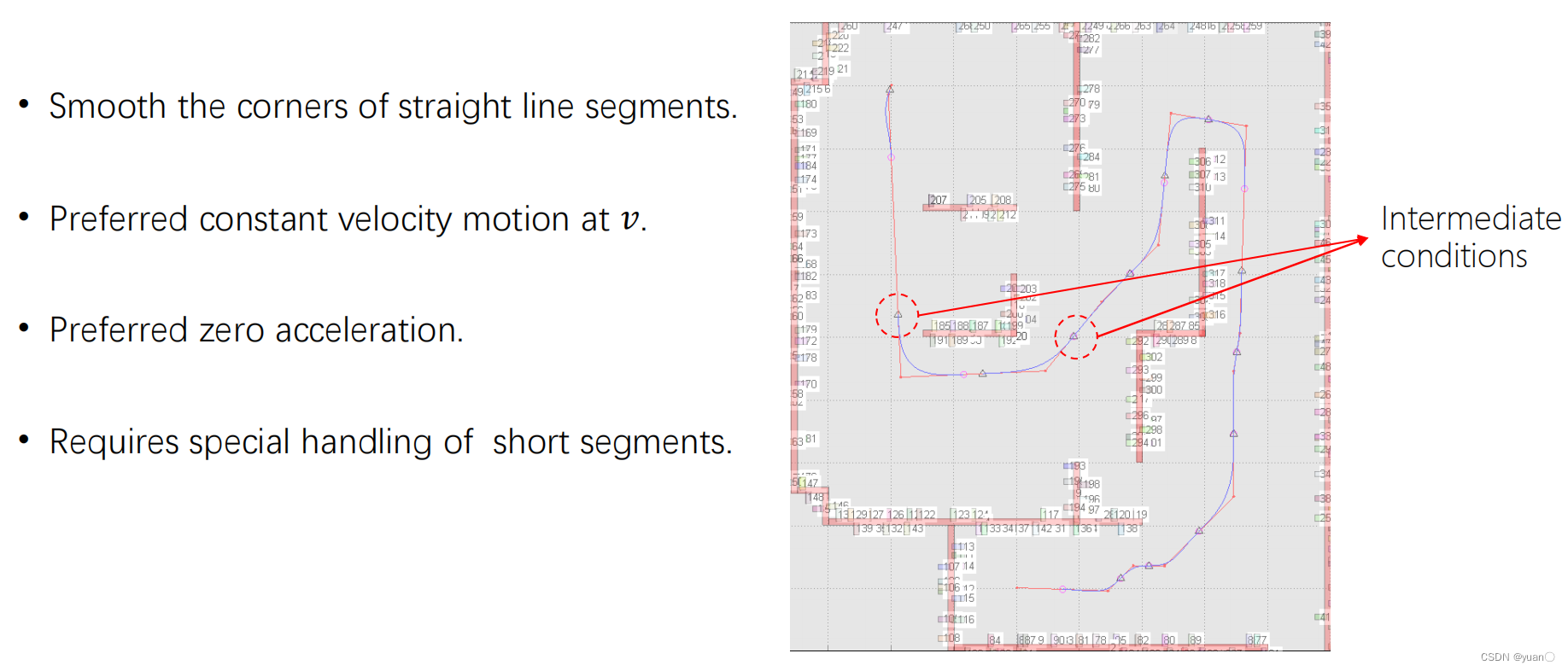
Las velocidades y aceleraciones para alcanzar estos puntos no son realmente fáciles de especificar.

Generación de trayectoria basada en optimización

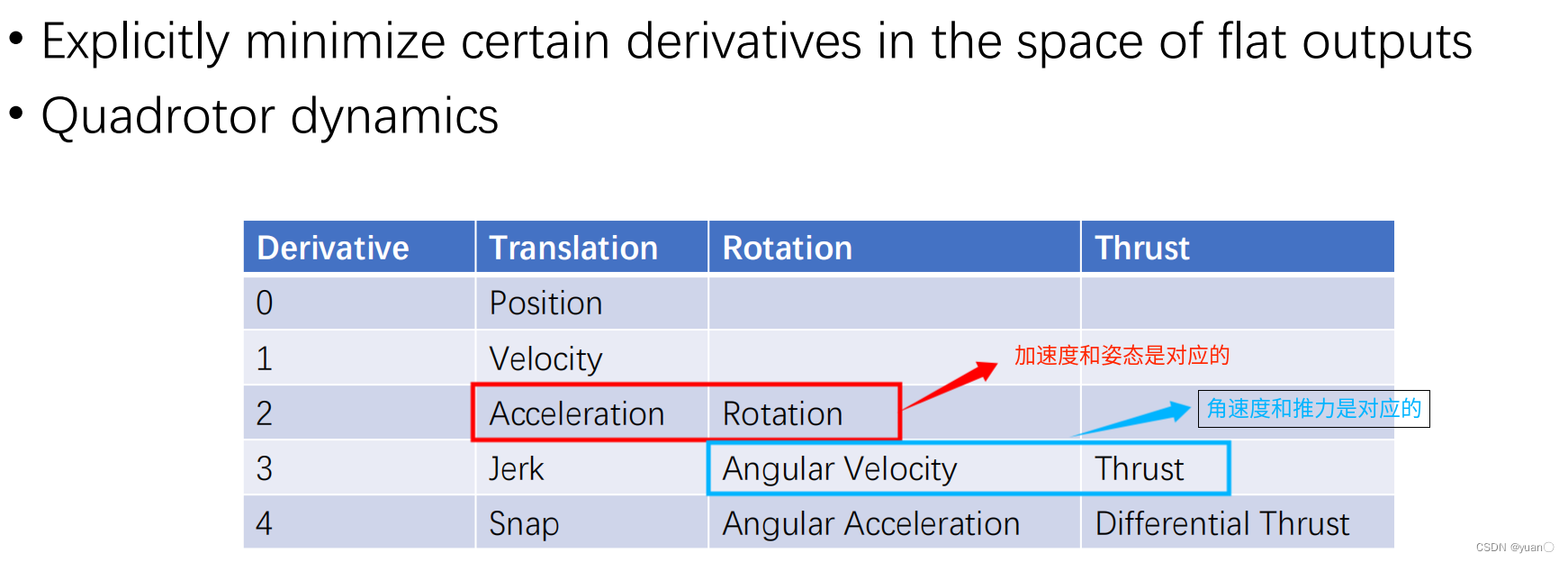
Minimizar el tirón es equivalente a la velocidad angular mínima, lo que puede obtener un mejor campo de visión de seguimiento visual
Minimizar el chasquido puede ahorrar energía

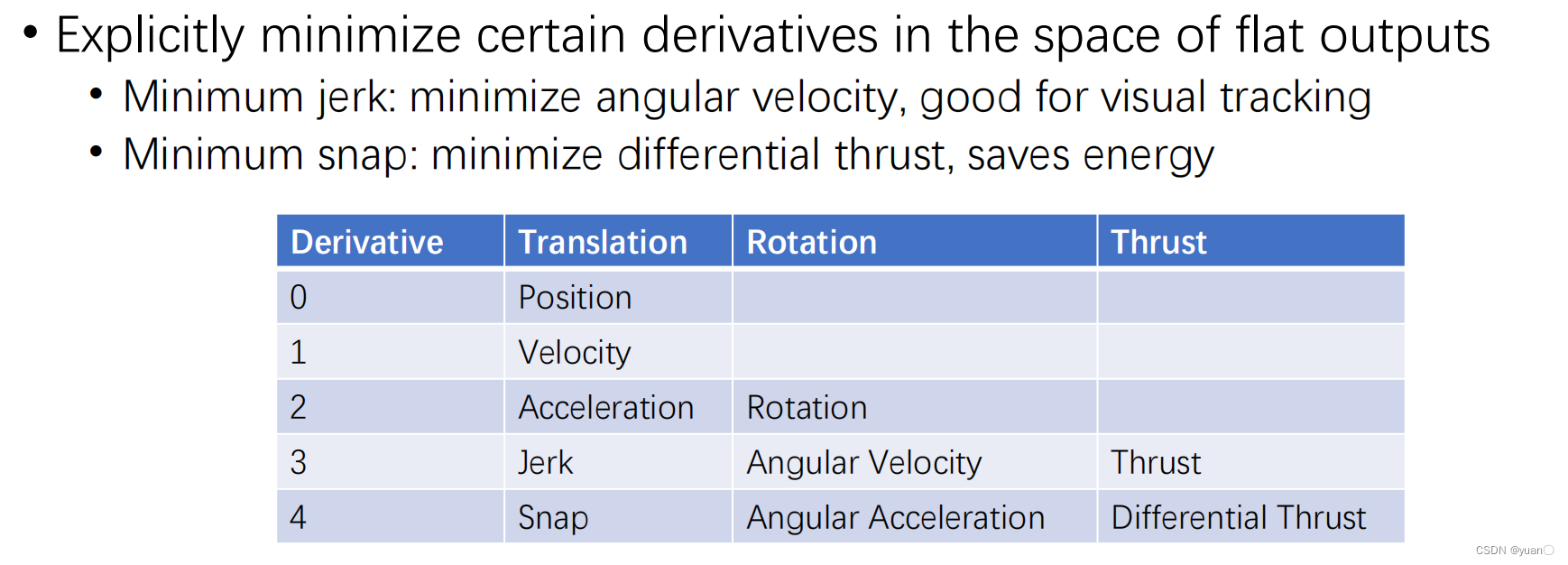
得到以下公式
f ( t ) = { F 1 ( t ) ≐ ∑ yo = 0 norte pags 1 , iti T 0 ≤ t ≤ T 1 F 2 ( t ) ≐ ∑ yo = 0 norte pags 2 , iti T 1 ≤ t ≤ T 2 ⋮ ⋮ F METRO ( t ) ≐ ∑ yo = 0 norte pags METRO , iti TM - 1 ≤ t ≤ TM f(t)=\begin{cases}f_1(t)\doteq\sum_{i=0} ^Np_{1,i}t^i&\quad T_0\leq t\leq T_1\\f_2(t)\doteq\sum_{i=0}^Np_{2,i}t^i&\quad T_1\leq t \leq T_2\\\vdots&\quad\vdots\\f_M(t)\doteq\sum_{i=0}^Np_{M,i}t^i&\quad T_{M-1}\leq t\leq T_M \end{casos}f ( t )=⎩ ⎨ ⎧F1( t )≐∑yo = 0nortepag1 , yotiF2( t )≐∑yo = 0nortepag2 , yoti⋮Fm( t )≐∑yo = 0nortepagM , yotyoT0≤t≤T1T1≤t≤T2⋮TMETRO - 1≤t≤Tm​

• cada segmento es un polinomio
• No se requiere necesariamente que el orden de cada trayectoria sea el mismo, pero el mismo puede simplificar el problema.
• El tiempo de cada trayectoria necesita ser conocido

Restricciones :

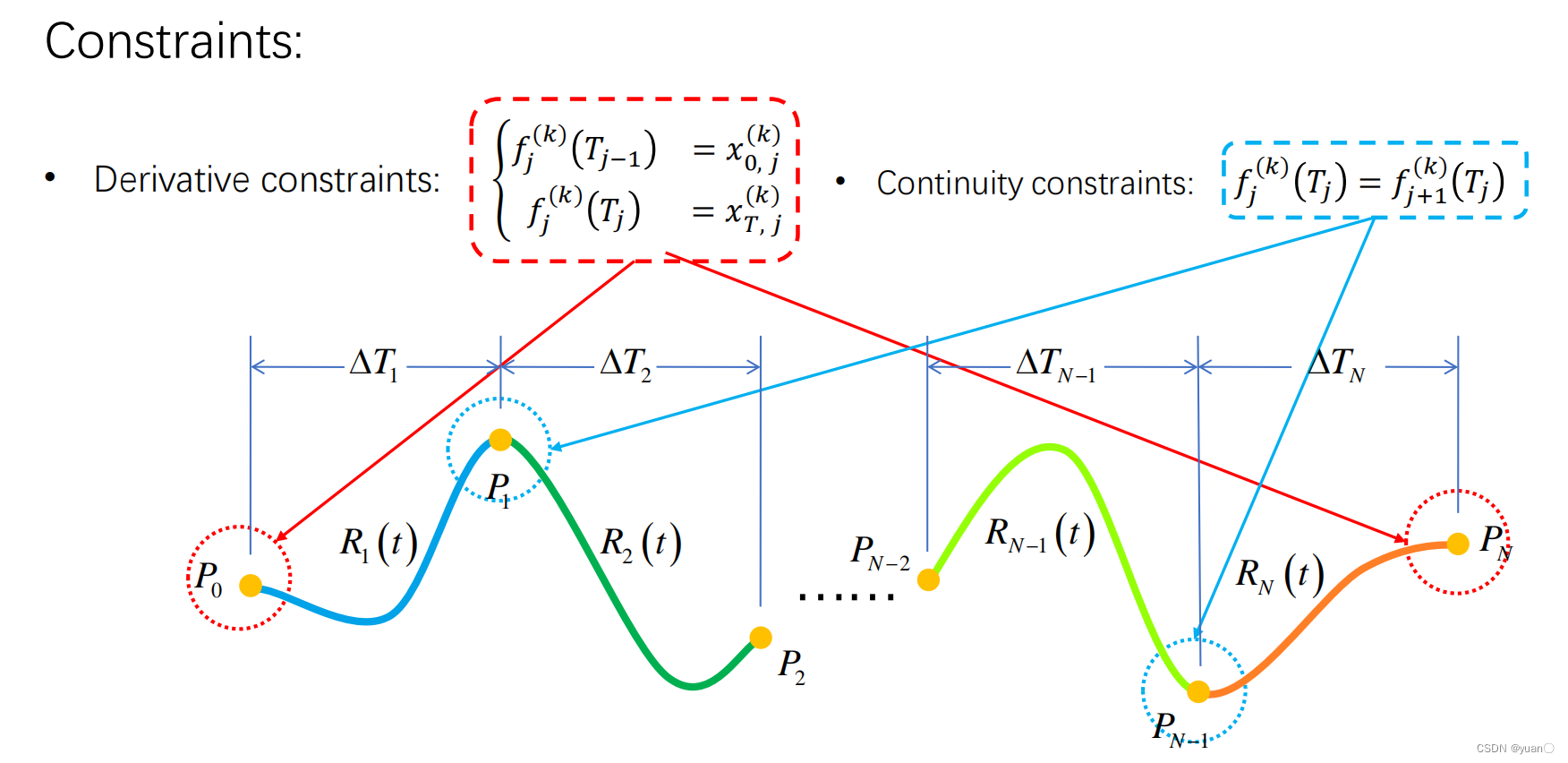
la suavidad de la trayectoria, la continuidad y la minimización de la entrada de control son independientes entre sí

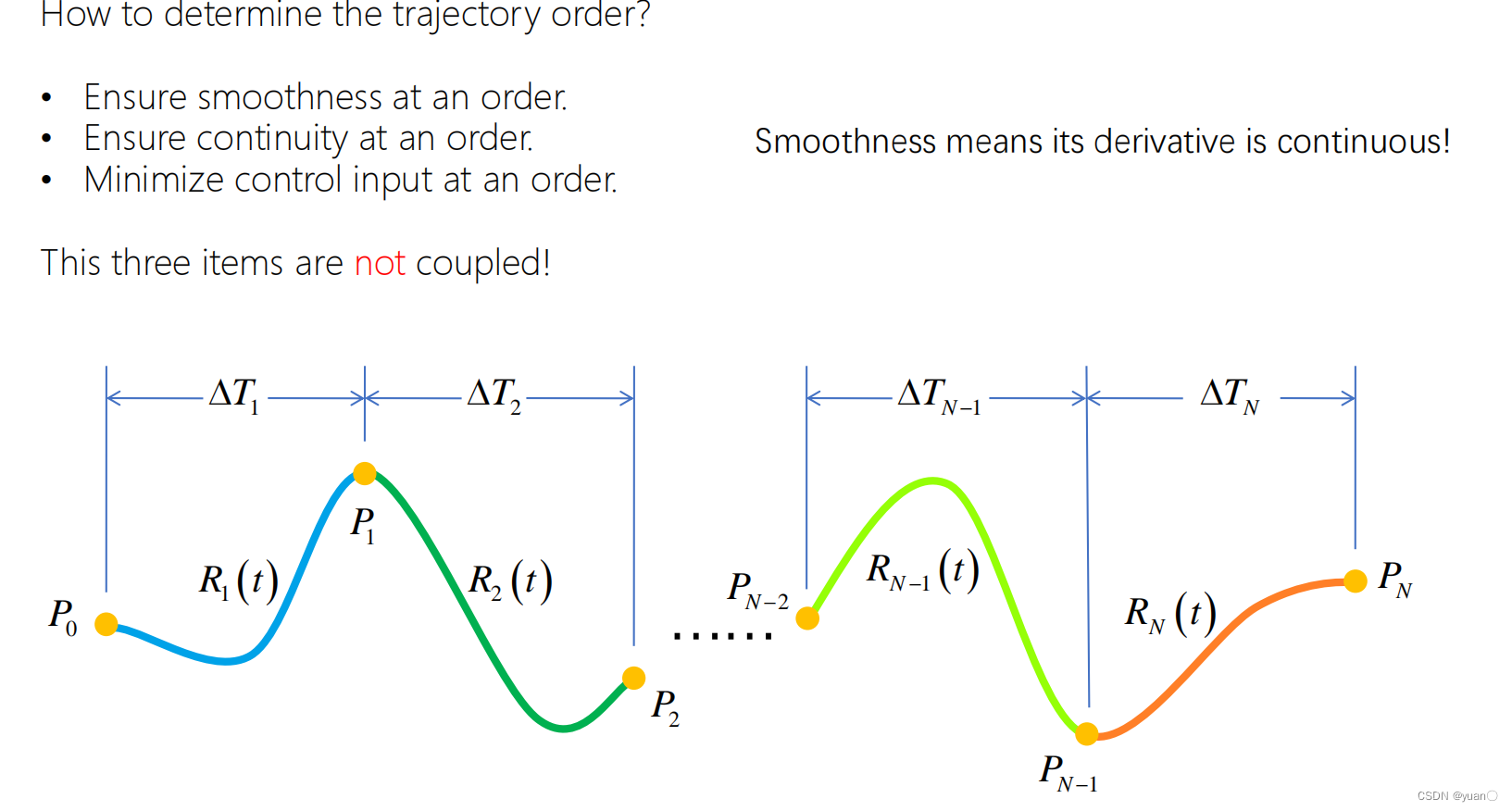
Minimizar el tirón requiere cinco trayectorias (una sección de trayectoria)
y minimizar el chasquido requiere siete trayectorias (una sección de trayectoria)

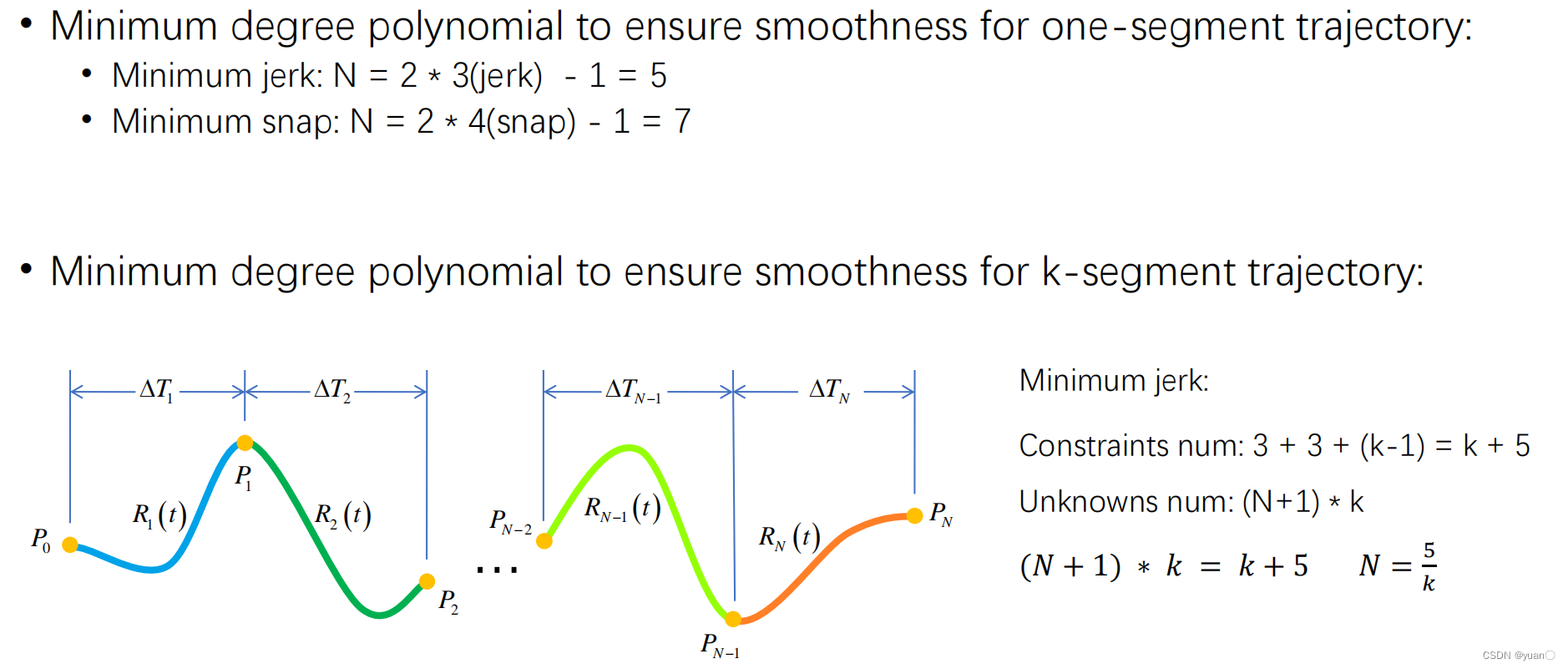
Configuración de la línea de tiempo

Una función objetivo de trayectoria

Restricciones diferenciales, k = 0, 1, 2, 3 para el punto inicial y el punto final, es decir, se requieren p, v, a, j; para el punto de ruta, generalmente se requiere k = 0, es decir, solo se requiere p , ambos casos se pueden escribir como una matriz Restricciones formales de igualdad

Restricciones de continuidad, aunque no se requieren v, a, j para el punto de ruta, pero se requiere que las derivadas de las trayectorias izquierda y derecha en el punto de ruta sean iguales

Optimizacion convexa

Cursos relacionados con la optimización convexa:

1. Clase abierta de Boyd Stanford
2. HKUST https://github.com/KellyHwong/convex-hkust
3. Recomendación y arreglo de libros de texto y cursos introductorios de optimización convexa

Funciones convexas y conjuntos convexos

La definición matemática de una función convexa es: si $f\left(x\right)$ en el intervalo$I$ enlace superior,$I$ es un intervalo en el conjunto de números reales, y para cualquier$x,y\in Sumo$ cualquier$yo\in [0,1]$ , tenemos$$f(\lambda x+(1-l\left)y\right)\le \lambda f\left(x\right)+(1-\lambda )f\left(y\right)$$则$f\left(x\right)$ en el intervalo$I$ es una función convexa. Entre ellos,$\lambda$ se llama el peso o relación de mezcla. Esta definición es en sentido geométrico, es decir, para dos puntos cualesquiera de la función, el valor de la función en cada punto del segmento de línea entre estos dos puntos no excede el valor de la función lineal correspondiente al punto. Una función convexa también se puede definir en forma de segunda derivada como$F^{\prime \prime }\left(x\right)\ge 0$ _
Definición matemática de conjunto convexo: En el espacio euclidiano, un conjunto$S$ es un conjunto convexo si y solo si para cualquier$x,y\in S$和$0\le yo\le 1$ ,都有
$$\lambda x+(1-l)y\in S$$ entre ellos,$\lambda$ es un número real, que representa$X_{}$y $X_{}$coeficiente de relación entre. En otras palabras, si el segmento de línea formado por dos puntos en cualquier conjunto está en el conjunto, entonces es un conjunto convexo.

La forma estándar de un problema de optimización convexo

$$\begin{array}{rl}minimizar& F_{}\left(X\right)\\ sujetoa& F_{}\left(X\right)\le 0i=1,\dots ,metro\\ & unax=\end{array}$$
donde la función objetivo $F_{}$y la función de restricción de desigualdad $F_{}\left(x\right)$ son funciones convexas,$unax=se\; requiere\; que\; b$ sea afín,xxSi el dominio de$x\; es\; un\; conjunto\; convexo$

Programación Lineal (LP): problemas de programación lineal

$$\begin{array}{rl}\underset{X}{}& C^{TX}\_+d\\ \text{sujeto a}& Gx\le h\\ & unax=\end{array}$$

Programación cuadrática (QP): problema de programación cuadrática

$$\begin{array}{rl}\underset{X}{}& \frac{}{2}{X}^{T}Px+q^{TX}\_+r\\ \text{sujeto a}& Gx\le h\\ & unax=\end{array}$$

QP con restricciones cuadráticas (QCQP): un problema de programación cuadrática con restricciones cuadráticas

QCQP (Programa cuadrático restringido cuadráticamente) se puede expresar de la siguiente forma:

$ $\begin{array}{rl}\underset{X}{}& (1/2){\times }^{TP}{\_}_{}X+q_0^{}X+r_{}\\ sujetoa& (1/2){\times }^{TP}{\_}_{}X+q_i^{}X+r_{}\le 0i=1,\dots ,metro\\ & unax=\end{array}$Las funciones de restricción también son funciones convexas.

donde $X\in R^n$ es la variable de optimización,${PAG}_{}\in S^{norte}$ ,${PAG}_{}\in S^{norte}$ ,$q_{},q_{}\in R^{norte}$ ,$b_{}\in R$ ,$A\in R^{p\times norte}$ ,$b\in R^{pags}$ ,$yo,tu\in R^n$ , y${yo}_{}\le {tu}_{}$。

donde, $S^n$ significa todos$norte\times$Una colección de matrices simétricas reales de$n\; .$$\frac{}{2}{X}^{TP}{\_}_{}X+q_i^{}X\le b_{}$expresar sobre xxRestricciones de desigualdad cuadrática en$x$$unax=b$ representa restricciones de igualdad lineal,${yo}_{}\le X_{}\le {tu}_{}$Representa las restricciones de los límites superior e inferior de las variables. El objetivo es minimizar la función objetivo $\frac{}{2}{X}^{TP}{\_}_{}X+q_0^{}x$ _

Programación de cono de segundo orden (SOCP): problema de optimización de segundo orden

SOCP es la abreviatura de programación de cono de segundo orden. La programación de conos cuadráticos se refiere a una clase de problemas de optimización convexos en los que las restricciones del problema de optimización consisten en conos cuadráticos.

La forma general de programación de cono cuadrático es:

$$\begin{array}{rl}\text{minimizar}& C^{TX}\_\\ \text{sujeto a}& ||A_{}X+b_{}|{|}_{}\le C_i^{}X+d_{},i=1,...,metro\\ & Fx=\end{array}$$

Entre ellos, $x$ es la variable de optimización,$c$ es un vector,$A_{}$es la matriz, $b_{}$es un vector, $d_{}$y $g$ es un escalar.

La restricción principal es la restricción del cono cuadrático, donde $||A_{}X+b_{}|{|}_{}\le C_i^{}X+d_{}$Representa el vector $A_{}X+b_{}$con el vector $C_i^{}X+d_{}$El producto interior en el espacio euclidiano es menor o igual a 0. Esta restricción se puede escribir en la forma transformada, a saber

$$\begin{array}{r}t\ge ||A_{}X+b_{}|{|}_{}\\ C_i^{}X+d_{}-t\le \end{array}$$

donde $t$ es una variable auxiliar utilizada para asegurar que el producto interno sea menor o igual a 0.

SOCP puede verse como un problema de PL directamente extendido. Por lo tanto, se puede resolver utilizando la optimización convexa, como el método de punto interior y el método de ramificación y límite. En comparación con la programación cuadrática, los problemas SOCP tienen mejor convexidad.

Programación Semidefinida（SDP）

SDP (Programación Semidefinida) se puede expresar de la siguiente forma:

$$\begin{array}{rl}\underset{X}{}& C^{TX}\_\\ s.t.& F_{}+\sum _{yo=1}{X}_{}{F}_{}⪰0\\ & X_{}⪰0,i=1,2,\dots ,\end{array}$$

其中，$X_{}\in S^{{norte}_{}}$es una matriz semidefinida positiva simétrica, $C\in R^n$ es un vector constante,$F_{}\in S^{{norte}_{}}$es una matriz simétrica constante, $F_{}\in S^{{norte}_{}}$es una matriz simétrica constante, $⪰0$ significa una matriz semidefinida positiva. El objetivo es minimizar la función objetivo$C^{T}x$, satisface la restricción de desigualdad matricial$F_{}+{\sum }_{yo=1}^{}{X}_{}{F}_{}⪰0$ y restricciones semidefinidas positivas$X_{}⪰0,i=1,2,\dots ,norte$ _

No es difícil ver que SDP puede considerarse como un problema de optimización convexo cuyas restricciones son matrices semidefinidas positivas simétricas. Las restricciones de desigualdad matricial garantizan que el problema es convexo.

Solución de forma cerrada para ajuste mínimo

Paper: Polynomial Trayectory Planning for Aggressive Quadrotor Flight in Dense Indoor Environments, Charles Richter, Adam Bry y Nicholas Roy
usan el solucionador QP para resolver la solución numérica del problema de ajuste mínimo. Otra solución es encontrar el ajuste mínimo directamente del álgebra. La solución analítica del problema, es decir, la solución de forma cerrada del problema de Snap Mínimo.

asignación de variables de decisión asignación de variables

Tomemos la ecuación:
$$j={\left[\begin{array}{c}{pag}_{}\\ ⋮\\ {pag}_{}\end{array}\right]}^T\left[\begin{array}{ccc}{q}_{}& 0& 0\\ 0& \ddots & 0\\ & & q_{}\end{array}\right]\left[\begin{array}{c}{pag}_{}\\ ⋮\\ {pag}_{}\end{array}\right]$$
Se puede observar que las variables optimizadas son los coeficientes del polinomio de trayectoria ${pag}_{},{pag}_{},...,{pag}_{}$, el coeficiente no tiene un significado físico real, como ${pag}_{}{t}^{10}$ en punto cuando$Cuando\; t$ es grande,${pag}_{}$Puede ser muy pequeño, lo que provocará inestabilidad numérica en problemas de planificación de trayectorias. Por lo tanto, necesitamos transformar el problema de los coeficientes en la optimización de la trayectoria en restricciones derivadas de los puntos de la trayectoria (es decir, $pag,v,a$ , tiene un significado físico). A través de la matriz de mapeo${METRO}_{}$La variable pj p_j a resolver${pag}_{}$Restricciones derivadas $d_{}$，即${METRO}_{}{pag}_{}=d_{}$。

Nueva función objetivo:

$$j={\left[\begin{array}{c}{d}_{}\\ ⋮\\ d_{}\end{array}\right]}^T{\left[\begin{array}{ccc}{METRO}_{}& 0& 0\\ 0& ⋮& 0\\ & & {METRO}_{}\end{array}\right]}^{-T}\left[\begin{array}{ccc}{q}_{}& 0& 0\\ 0& ⋮& 0\\ & & q_{}\end{array}\right]{\left[\begin{array}{ccc}{METRO}_{}& 0& 0\\ 0& ⋮& 0\\ & & {METRO}_{}\end{array}\right]}^{-1}\left[\begin{array}{c}{d}_{}\\ ⋮\\ d_{}\end{array}\right]$$

轨迹方程如下：
$$\begin{array}{rl}& x\left(t\right)={pag}_{}{t}^5+{pag}_{}{t}^4+{pag}_{}{t}^3+{pag}_{}{t}^2+{pag}_{}t+{pag}_{}\\ & X^{\prime }\left(t\right)=17:00{\_}_{}{t}^4+4p{\_}_{}{t}^3+3p{\_}_{}{t}^2+2p{\_}_{}t+{pag}_{}\\ & \begin{array}{r}{X}^{\prime \prime }\left(t\right)=20p{\_}_{}{t}^3+12{pags}_{}{t}^2+18:00{\_}_{}t+2p{\_}_{}\end{array}\end{array}$$

Razón:
$$METRO=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 2& 0& 0\\ T^5& T^4& T^3& T^2& T& 1\\ 5{toneladas}^4& 4{toneladas}^3& 3T{\_}^2& 2T\_& 1& 0\\ 20T{\_}^{}& 12{toneladas}^{}& 6& & & \end{array}\right]$$Para que quede más claro, $Las\; tres\; primeras\; filas\; de\; la\; matriz\; M$ serán$t=$Sustituya el valor en$0$$t=DenoteM$ pi = [ 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 2 0 0 T 5 T 4 T 3 T 2 T 1 5 T 4 4 T 3 3 T 2 2 T 1 0 20 T$$MP{\_}_{}=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 2& 0& 0\\ T^5& T^4& T^3& T^2& T& 1\\ 5{toneladas}^4& 4{toneladas}^3& 3T{\_}^2& 2T\_& 1& 0\\ 20T{\_}^{}& 12{toneladas}^{}& 6& & & \end{array}\right]\left[\begin{array}{c}{pag}_{}\\ {pag}_{}\\ {pag}_{}\\ {pag}_{}\\ {pag}_{}\\ {pag}_{}\end{array}\right]$$

Separación variable fija y variable libre Descomposición variable fija y variable libre

Las variables de estado del punto inicial y final en la trayectoria ( $pag,v,un,j$ ), se determina la posición del punto medio (waypoints)$\left(p\right)$ es determinista, por lo que al elegir la matriz$C$ para separar variables libres (gratis)$d_{}$Y la variable fija (restringida) $d_{}$. Por lo tanto, se puede obtener la siguiente relación de mapeo:
$$C^T\left[\begin{array}{c}{d}_{}\\ d_{}\end{array}\right]=\left[\begin{array}{c}{d}_{}\\ ⋮\\ d_{}\end{array}\right]$$Establezcamos las condiciones de contorno de la siguiente manera: $$j={\left[\begin{array}{c}{d}_{}\\ d_{}\end{array}\right]}^T\underset{R}{\underbrace{CM{\_}^{-T}Q{M}^{-1}{C}^T[\begin{array}{c}{d}_{}\\ d_{}\end{array}}}={\left[\begin{array}{c}{d}_{}\\ d_{}\end{array}\right]}^T\left[\begin{array}{cc}{R}_{}& R_{}\\ R_{}& R_{}\end{array}\right]\left[\begin{array}{c}{d}_{}\\ d_{}\end{array}\right]$$ Entonces, la función objetivo se convierte en un problema de programación cuadrática sin restricciones, que se puede resolver en forma cerrada$$\begin{array}{r}j=d_F^{}{R}_{}{d}_{}+d_F^{}{R}_{}{d}_{}+d_{PAG}^{}{R}_{}{d}_{}+d_{PAG}^{}{R}_{}{d}_{}\\ d_{PAG}^{}=-R_{PÁGINAS}^{-}{R}_{FP}^{}{d}_{}\end{array}$$
PD: ¿Por qué se ha ido la restricción de continuidad? Porque la matriz $C$ mapea una variable en$En\; las\; dos\; variables\; de\; d$ , se cumple la restricción de continuidad

CCdiseño de$c$

Enfoque jerárquico

Use RRT* para obtener waypoints, luego ajuste mínimo para generar trayectoria

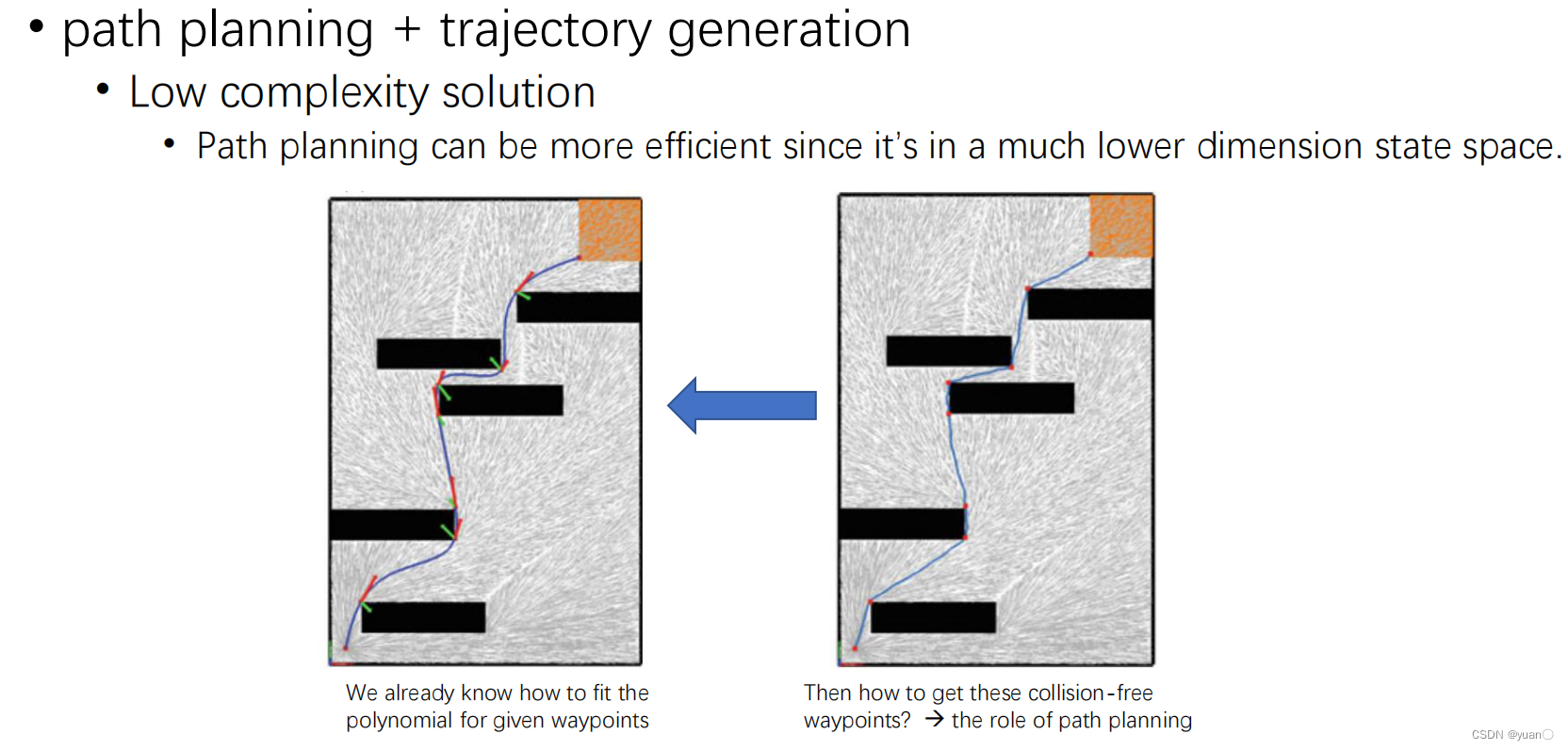
Problema: problema de seguridad

La ruta encontrada por RRT está libre de colisiones, pero se producirá un exceso después de la optimización de la trayectoria.

Solución: agregue un punto de ruta a la parte de colisión y regenere la trayectoria. Si todavía hay una colisión, continúe insertando puntos de ruta y genere en casos extremos. la trayectoria de estará infinitamente cerca de la ruta absolutamente segura de la planificación de la ruta

mejor solución?

Aumente el cuadro delimitador y realice la optimización de la trayectoria bajo restricciones estrictas (la próxima lección lo explicará en detalle).

Detalles de implementacion

Solucionadores convexos

solucionador	DIRECCIÓN	Ventajas y desventajas
CVX	http://cvxr.com/cvx/	Basado en la implementación de MATLAB, más lento
por Moisés	https://www.mosek.com/	Muy robusto, pero solo se ejecuta en arquitectura x86
OOQP	http://pages.cs.wisc.edu/~swright/ooqp/	Código rápido, de código abierto, robusto, pero antiguo, mala legibilidad
GLPK	https://www.gnu.org/software/glpk/	Código abierto, robusto, rápido, tiene ventajas en la solución de LP

Estabilidad numérica

Otras cosas de ingeniería

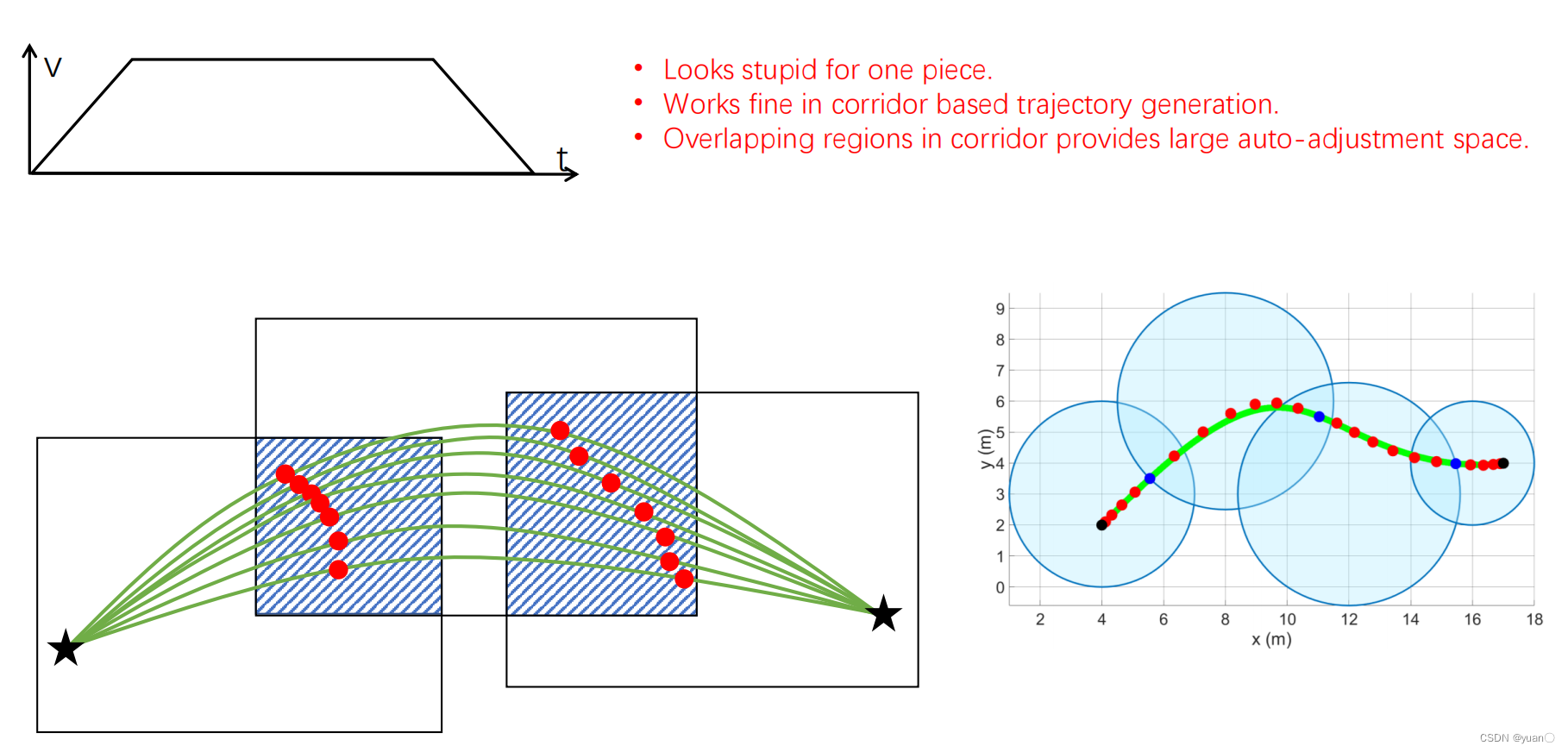
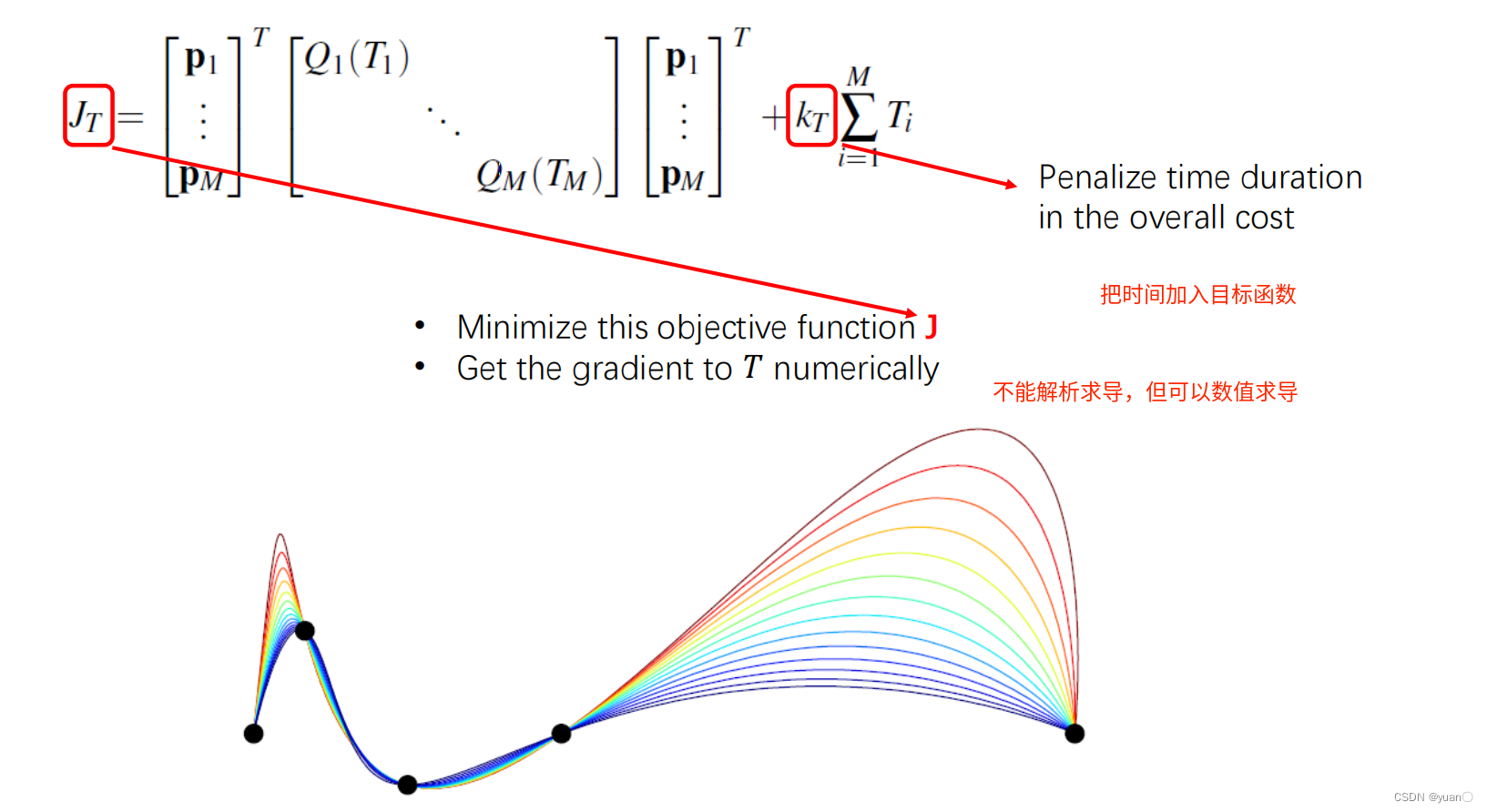
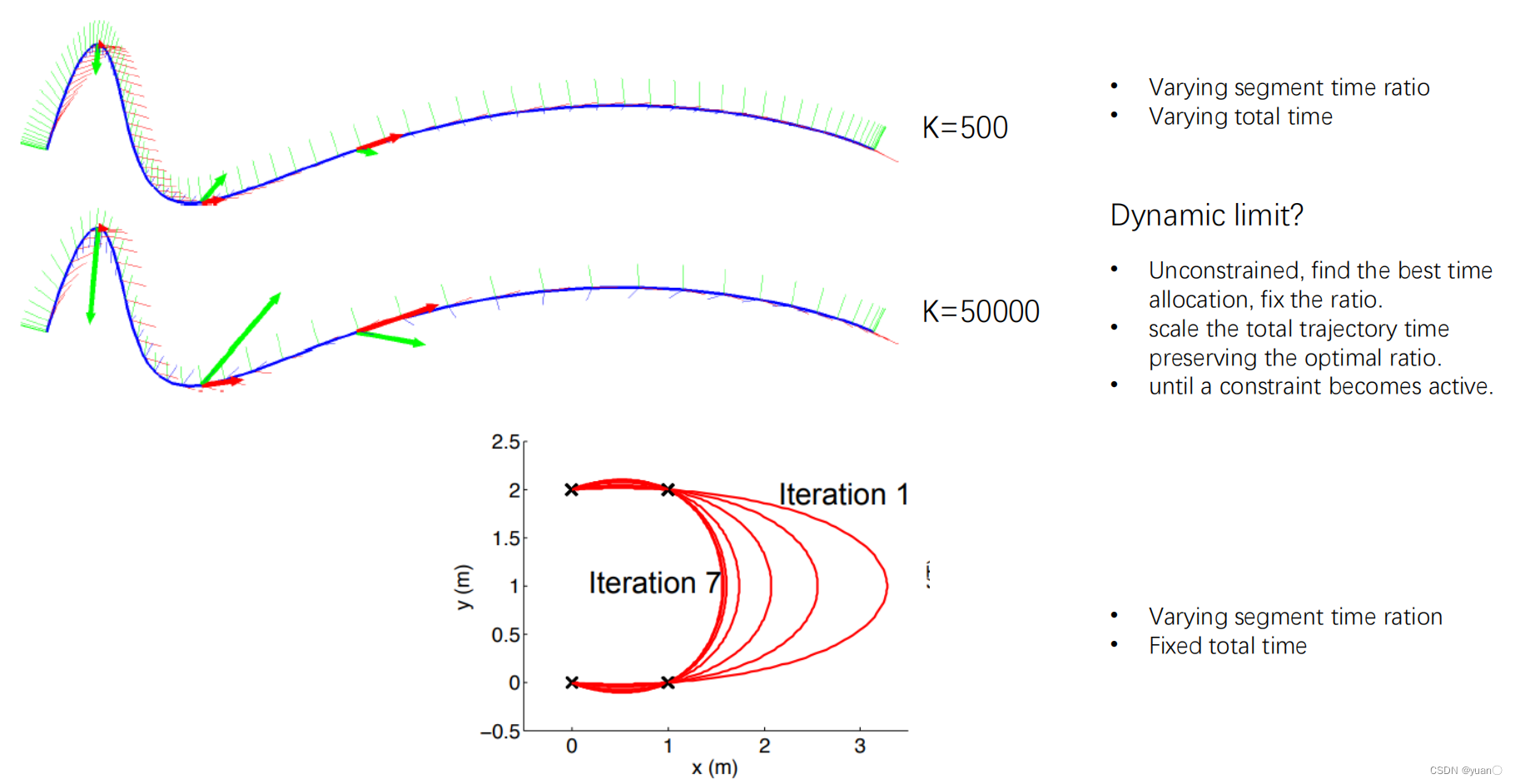
Asignación de tiempo asignación de tiempo

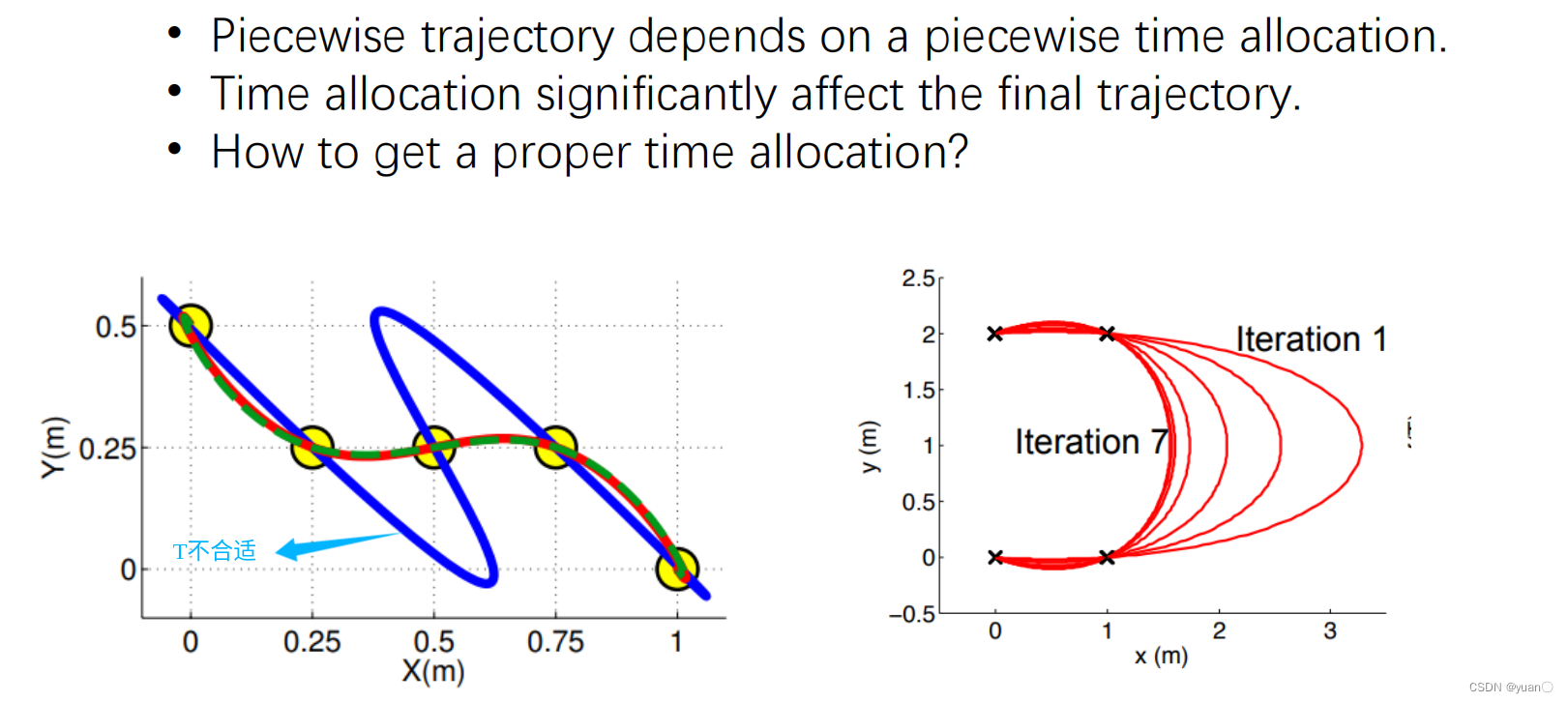
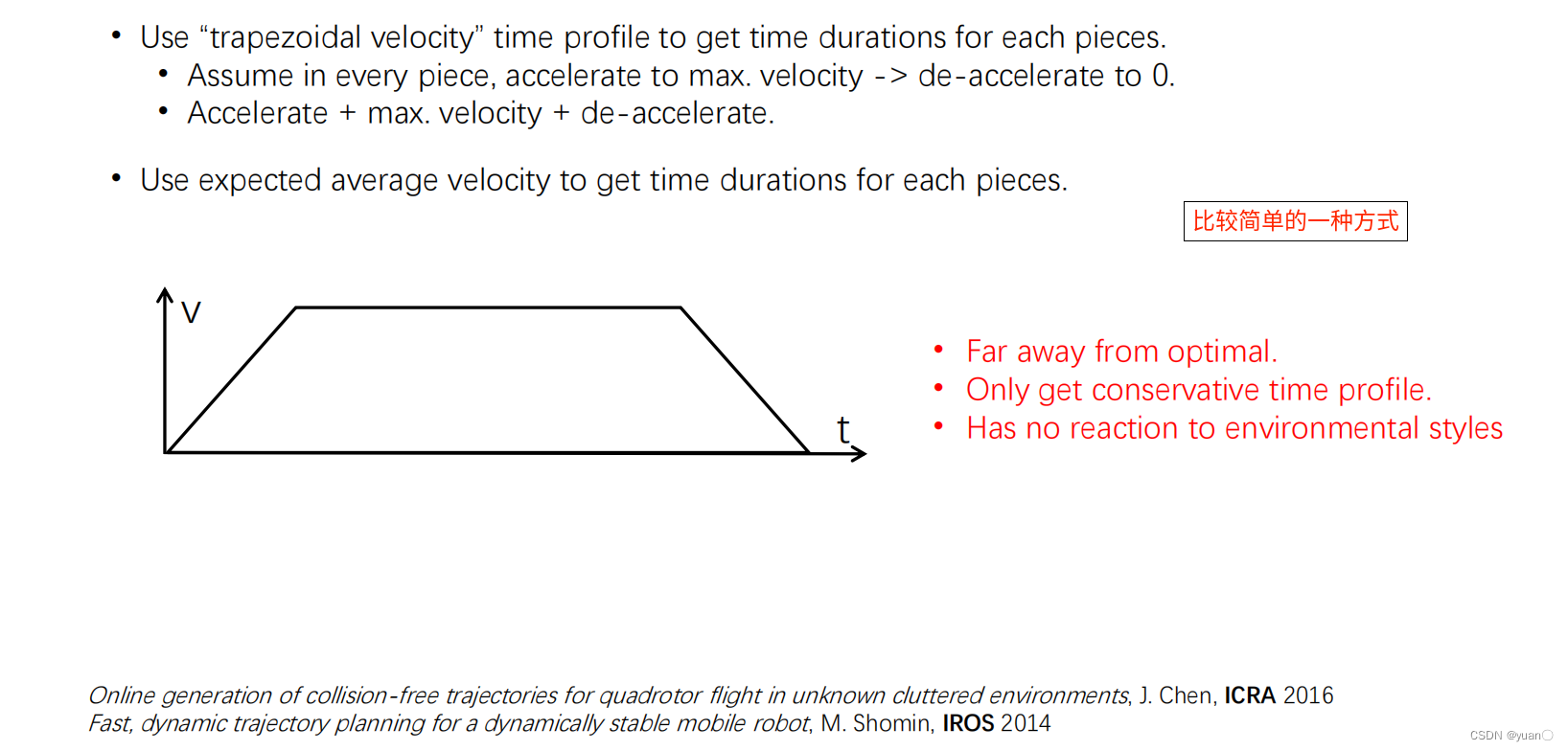
referencia

[1] Generación y control de trayectoria mínima instantánea para quadrotores, Daniel Mellinger y Vijay Kumar
[2] Planificación de trayectoria polinomial para vuelo agresivo de quadrotor en entornos interiores densos, Charles Richter, Adam Bry y Nicholas Roy

Consejos de codificación

Tome dos pistas como ejemplo:

solución cerrada

ROS:
solución cerrada