Análisis discriminante de Fisher con núcleos
Cuenta oficial: EDPJ
Tabla de contenido
0. Resumen
2. Discriminante lineal de Fisher
3. Fisher discriminante en el espacio de características
0. Resumen
Se propone una técnica de clasificación no lineal basada en el discriminante de Fisher. El ingrediente principal es el truco del núcleo, que permite el cálculo eficiente del discriminante de Fisher en el espacio de características. Una clasificación lineal en el espacio de características corresponde a una función de decisión no lineal (fuerte) en el espacio de entrada. Las simulaciones a gran escala demuestran la competitividad de nuestro método.
1. Análisis Discriminante
En la clasificación y otras tareas de análisis de datos, a menudo es necesario preprocesar los datos antes de aplicar el algoritmo en cuestión y, por lo general, primero extraer las características adecuadas para la tarea a resolver.
La extracción de características para la clasificación es muy diferente de la extracción de características para describir datos. Por ejemplo, PCA encuentra la dirección con el menor error de reconstrucción describiendo la mayor cantidad posible de variación de datos utilizando direcciones ortogonales. Consideran la primera dirección y no necesitan (de hecho, a menudo no lo hacen) revelar la estructura de clases que necesitamos para una clasificación correcta. El análisis discriminante aborda la siguiente pregunta: dado un conjunto de datos que contiene dos clases, digamos, ¿cuál es la mejor característica o conjunto de características (lineales o no lineales) para distinguir las dos clases? Los enfoques clásicos resuelven este problema utilizando (teóricamente) clasificadores bayesianos óptimos (suponiendo una distribución normal de clases) y algoritmos estándar (como el análisis discriminante cuadrático o lineal), que incluyen el famoso discriminante de Fisher. Por supuesto, se puede asumir cualquier otro modelo que no sea el modelo gaussiano para la distribución de clases, sin embargo, esto generalmente se logra a expensas de soluciones simples de forma cerrada.
En este trabajo, proponemos definir una generalización del discriminante no lineal de Fisher usando ideas de kernel originalmente aplicadas a máquinas de vectores de soporte (SVM), kernel PCA y otros algoritmos basados en kernel. Nuestro enfoque utiliza espacios de características del kernel para producir algoritmos altamente flexibles que resultan ser competitivos con las SVM.
Tenga en cuenta que existe una variedad de métodos llamados Análisis Discriminante del Kernel. La mayoría de ellos tienen como objetivo reemplazar las estimaciones paramétricas de las distribuciones condicionales de clase con estimaciones no paramétricas del kernel. Aunque nuestro método puede verse como tal, es importante señalar que va un paso más allá al interpretar el núcleo como un producto escalar en otro espacio. Esto permite interpretaciones teóricamente plausibles así como atractivas soluciones de forma cerrada.
A continuación, primero revisaremos el discriminante de Fisher, aplicaremos la técnica del núcleo, luego informaremos los resultados de la clasificación y finalmente daremos nuestras conclusiones. En este artículo, solo nos centraremos en problemas de clasificación binaria y discriminantes lineales en el espacio de características.
2. Discriminante lineal de Fisher
![]()
muestras de dos clases diferentes, y usa la notación
![]()


![]()
S_B y S_W son las matrices de dispersión entre clases y dentro de clases, respectivamente. La intuición detrás de maximizar J(w) es encontrar la dirección que maximiza la media de clase proyectada (numerador) mientras minimiza la varianza de clase (denominador) en esa dirección. Pero también existe un método estadístico bien conocido para motivar la ecuación (1):
Contacto Clasificador bayesiano lineal óptimo : un clasificador bayesiano óptimo compara las probabilidades posteriores de todas las clases y asigna un patrón a la clase con la mayor probabilidad. Sin embargo, la probabilidad posterior generalmente se desconoce y debe estimarse a partir de una muestra finita. Para las distribuciones de la mayoría de las clases, esta es una tarea abrumadora y, a menudo, es imposible obtener estimaciones de forma cerrada. Sin embargo, al suponer que todas las clases siguen una distribución normal, se puede derivar un análisis discriminante cuadrático (que esencialmente mide la distancia de Mahalanobis de un modo al centro de la clase). Simplificando aún más el problema y asumiendo la misma estructura de covarianza para todas las clases, el análisis discriminante cuadrático se vuelve lineal. Para problemas de clasificación binaria, es fácil mostrar que el vector w que maximiza la ecuación (1) está en la misma dirección que el discriminante en el clasificador óptimo bayesiano correspondiente. Aunque se basa en fuertes suposiciones que no son ciertas en muchas aplicaciones, el discriminante lineal de Fisher ha demostrado ser muy poderoso. Una razón es, por supuesto, que los modelos lineales son bastante resistentes al ruido y es probable que no se sobreajusten. Sin embargo, es crucial la estimación de la matriz de dispersión, que puede estar muy sesgada. Cuando el tamaño de la muestra es pequeño en comparación con la dimensionalidad, el uso de estimaciones "complementarias" simples en la ecuación (2) dará como resultado una alta variabilidad. Se han propuesto diferentes formas de afrontar esta situación a través de la regularización, volveremos sobre este tema más adelante.
3. Fisher discriminante en el espacio de características
Claramente, los discriminantes lineales no son lo suficientemente complejos para la mayoría de los datos del mundo real. Para aumentar la expresividad del discriminante, podemos intentar modelar un clasificador bayesiano óptimo con una distribución más compleja, o buscar direcciones no lineales (o ambas). Como se mencionó anteriormente, asumir una distribución general puede causar problemas. Aquí restringimos nuestra búsqueda de direcciones no lineales asignando primero de forma no lineal los datos a algún espacio de características F y calculando allí el discriminante lineal de Fisher, produciendo así implícitamente un discriminante no lineal en el espacio de entrada.
Sea Φ una aplicación no lineal a algún espacio de características F. Para encontrar el discriminante lineal en F, necesitamos maximizar


![]()
donde ω ∈ F, S^Φ_B y S^Φ_W son las matrices correspondientes en F.
Introducción a la función kernel : Obviamente, si la dimensión de F es muy alta, incluso infinita, no se puede resolver directamente. Para superar esta limitación, usamos el mismo truco que en kernel PCA o máquinas de vectores de soporte. En lugar de mapear los datos explícitamente, buscamos un algoritmo que use solo el producto escalar (Φ(x) · Φ(y)) de los patrones de entrenamiento. Dado que podemos calcular de manera eficiente estos productos escalares, podemos resolver el problema original sin un mapeo explícito a F. Esto se puede lograr utilizando los núcleos de Mercer: estos núcleos k(x, y) calculan el producto escalar en algún espacio de características F, es decir, k(x,y) = (Φ(x) · Φ(y)). Las posibles opciones para k han resultado útiles, por ejemplo, en máquinas de vectores de soporte o kernel PCA es un RBF gaussiano
![]()
o núcleo polinomial, k(x, y) = (x · y)^d, donde c y d son constantes positivas.
Para encontrar el discriminante de Fisher en el espacio de características F, primero debemos formular la Ecuación (4) en términos del producto escalar de los patrones de entrada, que luego reemplazamos por alguna función kernel. De la teoría del kernel recurrente sabemos que cualquier solución ω ∈ F debe estar dentro del rango de todas las muestras de entrenamiento en F. Así podemos encontrar la expansión de w:

Usando la expansión (5) y la definición de m^Φ_i, tenemos
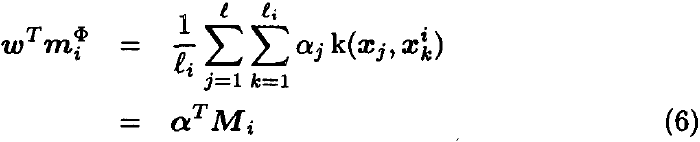
![]()
Ahora considere el numerador de la ecuación (4). Usando la definición de S^Φ_B y la ecuación (6), esto se puede reescribir como
![]()
![]()
Considerando el denominador de la ecuación (4), tenemos
![]()
![]()
![]()
![]()
![]()
I es la matriz identidad (Identidad).
Combinando las ecuaciones (7) y (8), podemos encontrar el discriminante lineal de Fisher en F maximizando la ecuación (9)

Este problema se puede resolver encontrando (N^(-1))M vectores propios principales (similar al algoritmo en el espacio de entrada). A este enfoque lo llamamos Kernel Fisher Discriminant (no lineal) (KFD). La proyección del nuevo patrón x sobre w viene dada por
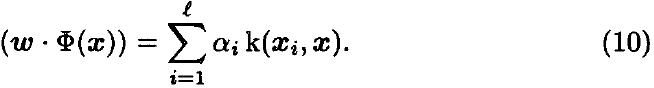
Cuestiones numéricas y regularización : Claramente, la configuración propuesta está mal condicionada: estamos estimando una estructura de covarianza L-dimensional a partir de t muestras. Además de los problemas numéricos que hacen que la matriz N sea no positiva, también necesitamos control de capacidad en F. Para hacer esto, simplemente sumamos múltiplos de la matriz identidad a N, es decir, reemplazamos N con
![]()
Esto se puede ver de diferentes maneras: (i) claramente hace que el problema sea más estable numéricamente, ya que N_μ se convierte en definido positivo para p lo suficientemente grande; (ii) reduce el sesgo en las estimaciones de valores propios basadas en muestras; (iii) impone un regularización en ||α||^2 (recuerde que estamos maximizando la ecuación (9)), favoreciendo soluciones con coeficientes de expansión pequeños. Si bien el verdadero impacto de esta configuración de regularización no se comprende completamente, muestra conexiones con las que se usan en las máquinas de vectores de soporte. Además, se podrían usar otros tipos de adiciones de regularización a N, por ejemplo, similar a la penalización de SVM ||ω||^2 (agregando la matriz de kernel completa K_ij = k(x_i, x_j)).
4. Experimenta

La figura 1 muestra las características encontradas por KFD en comparación con la primera y la segunda características (no lineales) encontradas por Kernel PCA en el conjunto de datos de juguetes. Para ambos, se utiliza un kernel polinomial de segundo orden, y para KFD, el diagrama de dispersión dentro de la clase se regulariza con μ = 10^(-3). Representa dos clases (cruces y puntos), valores de características (representados por niveles de gris) y líneas de contorno de las mismas características. Cada categoría consta de dos formas parabólicas ruidosas reflejadas en el eje x y el eje y respectivamente. Vemos que las características de KFD discriminan las dos clases de una manera casi óptima, mientras que las características de Kernel PCA, aunque describen propiedades interesantes del conjunto de datos, no lo hacen tan bien (aunque las características de Kernel PCA de orden superior también pueden ser discriminatorias).
Para evaluar el rendimiento de nuestro nuevo método, realizamos extensas comparaciones con otros clasificadores de última generación. Comparamos el discriminante Kernel Fisher con AdaBoost, AdaBoost regularizado y máquinas de vectores de soporte (con núcleos gaussianos). Para KFD, también usamos un núcleo gaussiano para regularizar la dispersión dentro de la clase. Después de encontrar la mejor dirección ω ∈ F, calculamos su proyección usando la Ecuación (10). Para estimar el umbral óptimo para extraer características, se puede utilizar cualquier técnica de clasificación, por ejemplo, tan simple como ajustar un sigmoide. Aquí usamos un SVM lineal (optimizado por descenso de gradiente ya que solo tenemos muestras 1D). Sin embargo, una desventaja de esto es que tenemos otro parámetro para controlar, la constante de regularización en el SVM.
Utilizamos 13 conjuntos de datos artificiales y del mundo real (excepto bananas) de los repositorios de referencia UCI, DELVE y STATLOG. Los problemas no binarios se dividen en dos tipos de problemas. Luego genere 100 particiones para probar y entrenar conjuntos (aproximadamente 60%:40%). En cada uno de estos conjuntos de datos, entrenamos y probamos todos los clasificadores. Los resultados de la Tabla 1 muestran el error de prueba medio y la desviación estándar para estas 100 ejecuciones. Para estimar los parámetros necesarios, realizamos una validación cruzada de 5 veces en las primeras cinco realizaciones del conjunto de entrenamiento y usamos los parámetros del modelo como la mediana de las cinco estimaciones.

Además, en nuestros experimentos preliminares usando KFD en el conjunto de datos de dígitos escritos a mano de USPS, restringimos la expansión de w en la Ecuación (5) para que solo se ejecute en las primeras 3000 muestras de entrenamiento. Logramos un error de 10 categorías del 3,7 % con un kernel gaussiano de 0,3 x 256 de ancho, que es ligeramente mejor que SVM con un kernel gaussiano (4,2 %).
Resultados experimentales : los experimentos muestran que el discriminante de Kernel Fisher (más las máquinas de vectores de soporte para estimar el umbral) es competitivo en casi todos los conjuntos de datos (excepto imágenes) o, en algunos casos, incluso supera a otros algoritmos. Curiosamente, tanto SVM como KFD construyen un hiperplano óptimo (en cierto sentido) en F, mientras que notamos que la solución de KFD w da un hiperplano que suele ser mejor que la solución SVM.
5. Discusión y conclusiones
El discriminante de Fisher es una de las técnicas lineales estándar en el análisis de datos estadísticos. Sin embargo, los métodos lineales a menudo son demasiado limitados y en el pasado se han utilizado varios métodos para derivar criterios de separabilidad de clases más generales. Sin embargo, nuestro enfoque tiene mucho de este espíritu, dado que calculamos la función discriminante en algún espacio de características F (no linealmente relacionado con el espacio de entrada), todavía podemos encontrar soluciones de forma cerrada y preservar la belleza teórica de Fisher. análisis discriminante. Además, los diferentes núcleos permiten un alto grado de flexibilidad debido a la amplia gama de posibles no linealidades.
Nuestros experimentos muestran que KFD es competitivo con otras técnicas de clasificación de última generación. Además, dado que el análisis discriminante lineal es un campo bien estudiado y muchas ideas desarrolladas previamente en el espacio de entrada se pueden transferir al espacio de características, todavía hay mucho espacio para la expansión y la teoría adicional.
Tenga en cuenta que, si bien la complejidad de SVM aumenta con la cantidad de vectores de soporte, KFD no tiene un concepto de SV y su complejidad aumenta con la cantidad de imágenes de entrenamiento. Por otro lado, especulamos que parte del rendimiento de KFD sobre SVM puede estar relacionado con el hecho de que KFD usa todas las muestras de entrenamiento en la solución, no solo las duras, es decir, los vectores de soporte.
El trabajo futuro se dedicará a encontrar esquemas de aproximación y algoritmos numéricos adecuados para obtener los vectores propios principales de matrices grandes. Otras áreas de investigación incluirán la construcción de discriminantes multiclase, el análisis teórico de los límites de error de generalización de KFD y la investigación del vínculo entre KFD y las máquinas de vectores de soporte.
referencia
Mika S, Ratsch G, Weston J, et al. Análisis discriminante de Fisher con núcleos[C]//Redes neuronales para el procesamiento de señales IX: Actas del taller de la sociedad de procesamiento de señales IEEE de 1999 (cat. n.º 98th8468). iee, 1999: 41-48.
S. Resumen
S.1 Idea principal
Para la mayoría de las clasificaciones de datos del mundo real, el discriminante lineal no es lo suficientemente complejo. Para aumentar la expresividad discriminativa, se pueden usar distribuciones más complejas para modelar clasificadores bayesianos óptimos o para encontrar direcciones no lineales (o ambas).
El modelo lineal es bastante resistente al ruido y es probable que no se sobreajuste, pero la estimación de la matriz de dispersión crucial puede estar muy sesgada, especialmente cuando el tamaño de la muestra es pequeño en comparación con la dimensionalidad.
Método S.2
Los datos primero se asignan de forma no lineal a algún espacio de características F, y el discriminante lineal de Fisher se calcula allí para encontrar la dirección no lineal, produciendo así implícitamente un discriminante no lineal en el espacio de entrada.
En lugar de mapear explícitamente los datos, los autores buscan un algoritmo que use solo el producto escalar del patrón de entrenamiento (Φ(x) · Φ(y)), donde Φ es un mapeo no lineal a algún espacio de características F. Dado que estos productos punto se pueden calcular de manera eficiente, el problema original se puede resolver sin un mapeo explícito a F. Esto se puede lograr utilizando los núcleos de Mercer: estos núcleos k(x, y) calculan el producto escalar en algún espacio de características F, es decir, k(x,y) = (Φ(x) · Φ(y)).
Función de kernel k, por ejemplo, Gaussian RBF en SVM o Kernel PCA
![]()
o núcleo polinomial, k(x, y) = (x · y)^d, donde c y d son constantes positivas.