Tabla de contenido

En el diseño de hardware, la multiplicación es mucho mayor que la suma en términos del uso de recursos lógicos y el retraso de la lógica combinacional . Desde la perspectiva del hardware, estamos más inclinados a convertir la multiplicación en desplazamiento y suma, por ejemplo, multiplicar por 8 se puede convertir en un desplazamiento a la izquierda de 3 bits. A*15 se puede convertir a (A<<4) - A, y la multiplicación se puede convertir en otras operaciones para reducir el consumo de recursos y el retraso de la lógica combinacional.

Pero a veces, cuando el valor multiplicado no es un valor fijo, es difícil para nosotros convertir la multiplicación en cambio y suma en el hardware, por lo que cuando no se puede evitar la multiplicación, es muy importante cómo reducir el número de multiplicaciones.

Algoritmo de Gauss

Multiplicación óptima del algoritmo de Gauss

$(a+bi)*(c+di) = (ac -bd) + (bc + ad )i$

Al calcular (a+bi)*(c+di), el número total de multiplicaciones involucradas es cuatro multiplicaciones y tres sumas.

Optimizado usando el algoritmo de Gauss:

$\begin{c} \\k_{1} = c * (a+b) \\ k_{2} = a*(dc) \\k_{3} =b*(c+d)\\ \\Real_ {1} = k_{1}-k_{3} \\Imaginario_2 = k_1+ k_2 \end{c}$

Después de ser optimizado por el algoritmo de Gauss, la parte real es $Real$ , y la parte imaginaria es $Imaginar$ . La cantidad total del cálculo ha cambiado de las 4 multiplicaciones + 3 sumas originales a 3 multiplicaciones + 5 sumas, lo que reduce el número de multiplicaciones.

Algoritmo de Strassen

La multiplicación de matrices anterior usa un total de 8 multiplicaciones + 4 sumas.

El algoritmo de Strassen es muy similar al algoritmo de Gauss, y el método de optimización es el siguiente:

$\\P_1=a(fh),\ P_2=(a+b)h,\ P_3=(c+d)e\ P_4=d(ge) \\P_5=(a+d)(e+h), \ P_6=(bd)(g+h),\ P_7=(ac)(e+f)$

$resultados: AB=\begin{bmatrix} P_5+P_4-P_2+P_6&P_1+P_2 \\ P_3+P_4&P_1+P_5-P_3-P_7 \end{bmatrix}$

El algoritmo de Strassen aplicado a la multiplicación de matrices 2X2 puede convertir 8 multiplicaciones + 4 sumas en 7 multiplicaciones + 18 sumas.

Si la matriz B es una constante, como una matriz de peso. Entonces el algoritmo de Strassen puede convertir 8 multiplicaciones + 4 sumas en 7 multiplicaciones + 13 sumas , reduciendo el número de multiplicaciones .

El algoritmo de Strassen reduce la complejidad de la multiplicación de matrices de Θ(N 3 ) a Θ(N 2.807 ) al reducir el número de multiplicaciones. El costo de reducir el número de cálculos es que se requiere más memoria.

Algoritmo de Winograd

Winograd es un algoritmo rápido para calcular circunvoluciones cortas.

La operación de convolución unidimensional se define como F( m,r ) , m es Tamaño de salida , r es Tamaño de filtro, luego la longitud de la señal de entrada es m+r−1:

La operación de convolución consiste en multiplicar las posiciones correspondientes y luego sumarlas. Cada posición de la señal de entrada debe participar en al menos una multiplicación, por lo que el número de multiplicaciones es al menos igual a la longitud de la señal de entrada, que se registra como:

$\\u(F(m,r)) = m + r-1$

Realice operaciones de convolución unidimensional en las filas y columnas respectivamente para obtener una convolución bidimensional, que se registra como F( m×n,r×s ) , la salida es m×n y el kernel de convolución es r×s , entonces la señal de entrada es ( m+r−1)(n+s−1), el número de multiplicaciones es al menos μ(F(m×n,r×s))=μ(F(m,r)) μ(F(n,s)) =(m+r−1)(n+s−1).

Vid 1D

La señal de entrada es $d = [d_0\ d_1\ d_2\ d_3]^T$ , el kernel de convolución es $g =[g_0\ g_1\ g_2]^T$ , la entrada es una matriz de 1 * 4 y el kernel de convolución es una matriz de 1 * 3. El resultado de la convolución de los dos obtendrá dos valores. El proceso de convolución anterior se puede escribir como siguiente forma $F(2,3)=\begin{bmatriz} d_0 &d_1 &d_2 \\ d_1&d_2 &d_3 \end{bmatriz} \begin{bmatriz} g_0\\g_1 \\ g_2 \end{bmatriz}=\begin{bmatriz} r_0\\ r_1 \end{bmatriz}$

Si es una multiplicación general de matrices, se requieren 6 multiplicaciones y 4 sumas , y el proceso es el siguiente:

$\\r_0=(d_0*g_0)+(d_1*g_1)+(d_2*g_2)\\ r_1 =(d_1*g_0)+(d_2*g_1)+(d_3*g_2)$

El algoritmo de Winograd es una operación orientada a la convolución en lugar de una multiplicación de matriz normal:

$F(2,3)=\begin{bmatriz} d_0 &d_1 &d_2 \\ d_1&d_2 &d_3 \end{bmatriz} \begin{bmatriz} g_0\\g_1 \\ g_2 \end{bmatriz}=\begin{bmatriz} m_1+m_2 +m_3 \\ m_2-m_3-m_4 \end{bmatriz}$

en:

$\\m_1=(d_0-d_2)g_0\ \ \ \ \ m_2=(d_1+d_2)\frac{g_2+g_1+g_2}{2}\\ m_4=(d_1-d_3)g_2\ \ \ \ \ m_3 =(d_2-d_1)\frac{g_0-g_1+g_2}{2}$

El cálculo de Winograd requiere 4 multiplicaciones + 12 sumas + 2 turnos . Si el filtro del kernel de convolución $soldado americano$ es una constante, por ejemplo, el filtro es una matriz de peso fijo, el cálculo de Winograd requiere 4 multiplicaciones + 8 adiciones .

Por conveniencia, Winograd 1D se puede expresar como:

$Y=A^T [(Gg)\odot (B^T d)]$

donde $\odot$ está el producto escalar, que es la multiplicación de bits. $B^T$ Es una matriz de transformación de entrada con un tamaño de $(m+r-1)\veces(m+r-1)$ , G es una matriz de transformación de filtro con un tamaño de $(m+r-1)\veces r$ r $A^T$ y una matriz de transformación de salida con un tamaño de $m\veces(m+r-1)$ :

$B^T=\begin{bmatrix} 1&0 &-1 &0 \\ 0&1 &1 &0 \\ 0& -1 & 1 &0 \\ 0& 1 &0 &-1 \end{bmatrix} ,\ G=\begin{bmatrix} 1& 0 &0 \\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2} \\ \frac{1}{2}& -\frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 1 \end{bmatrix}, \ A^T=\begin{bmatrix} 1 &1 & 1 & 0\\ 0& 1& -1& -1 \end{bmatrix }$

gNúcleo de convolución: $g=\begin{bmatriz} g_0&g_1 &g_2 \end{bmatriz}^T$ ;dSeñal de entrada: $d=\begin{bmatriz} d_0 &d_1 &d_2 &d_3 \end{bmatriz}^T$ , trayendo estas matrices a la ecuación Y, se puede derivar el mismo resultado que el F(2,3) anterior.

Vid 2D

De acuerdo con la fórmula Winograd 1D, se puede simplificar de la siguiente manera:

$Y=A^T [(Gg)\odot (B^T d)]=A^T [(GgG^T)\odot (B^T dB)]A$

Para la convolución bidimensional, como se muestra en la figura de la derecha, se utiliza un núcleo de convolución de 3 x 3 para convolucionar un área de 4 x 4 y se realizarán un total de cuatro convoluciones. en uno La matriz de 9*1, el área de 4*4 se expande en una matriz de 4*9 de acuerdo con el método de multiplicación con el núcleo de convolución, de modo que el producto de la matriz de expansión de área de 4*9 y el núcleo de convolución de 9*1 matriz de expansión Todavía igual al resultado de la convolución:

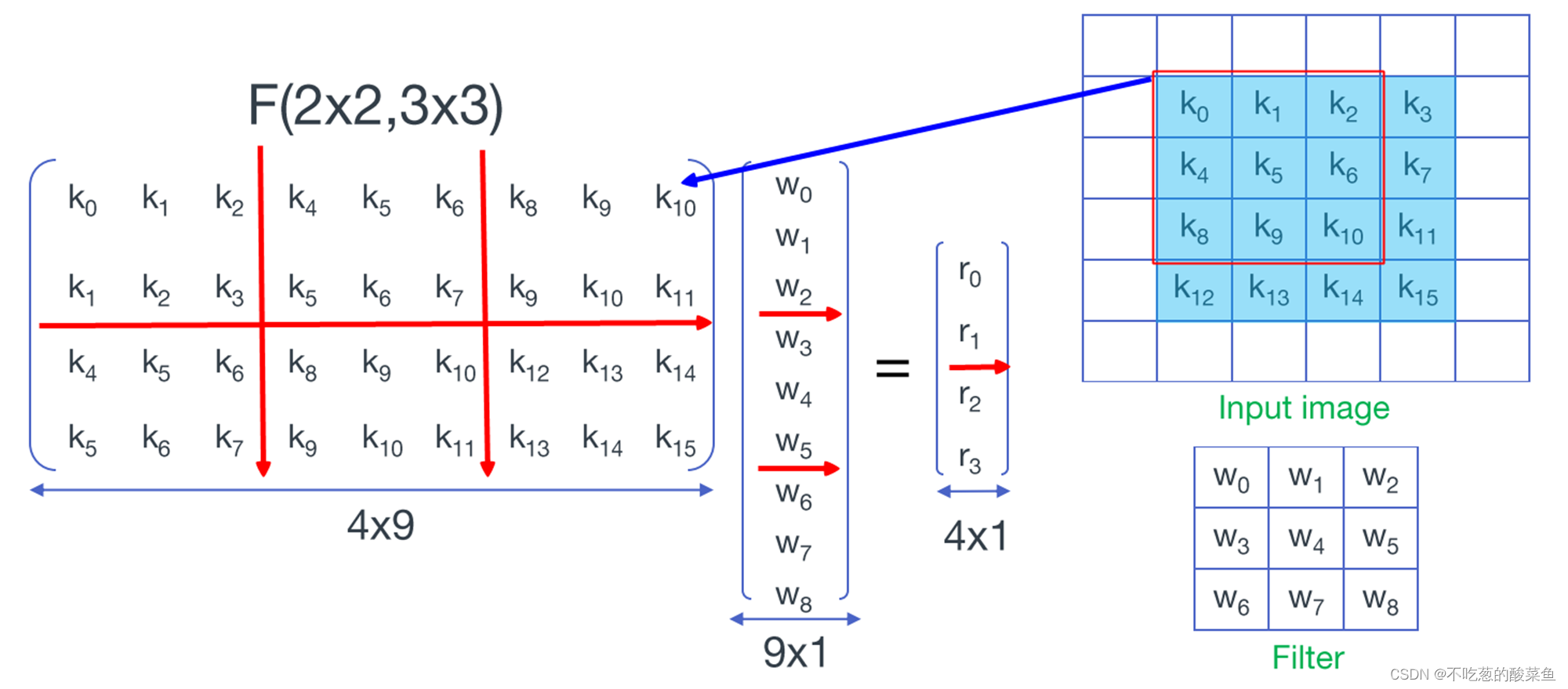
A través de la optimización de la manera anterior, convertimos con éxito la convolución 2D en multiplicación 1D, y luego podemos usar la fórmula de simplificación de Winograd 1D para optimizar la multiplicación de convolución.

La posición de los elementos repetidos en cada submatriz es la misma que en unidimensional, y la submatriz repetida también es la misma que en unidimensional

Podemos reutilizar el módulo de multiplicación de Winograd 1D a 2D:

$F(2,3)=\begin{bmatriz} d_0 &d_1 &d_2 \\ d_1&d_2 &d_3 \end{bmatriz} \begin{bmatriz} g_0\\g_1 \\ g_2 \end{bmatriz}=\begin{bmatriz} r_0\\ r_1 \end{bmatriz}$

Orden , es decir, el elemento de fila 0 en la ventana , significa la fila 1 , 2 , 3, por lo que podemos deducir los siguientes resultados: $D_0=[k_0,k_1,k_2,k_3]^T$ $D_1, D_2, D_3$ $W_0=[w_0,w_1,w_2]^T$

En términos simples, 1D Winograd está anidado en 2D Winograd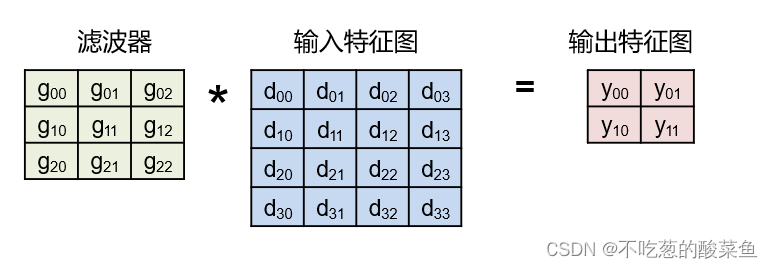

Para la multiplicación anterior, la convolución directa realizará 36 multiplicaciones (4 * 9). Usando el algoritmo de Winograd, el número de multiplicaciones se puede reducir a 16 veces, lo que se reduce en 2,25 veces, lo que tiene un efecto significativo en la convolución optimizada. algoritmo.

Algoritmos optimizados para reducir el número de multiplicaciones (Gauss, Strassen, Winograd)

Algoritmo de Gauss

Algoritmo de Strassen

Algoritmo de Winograd

Vid 1D

Vid 2D

Supongo que te gusta