数据结构与算法之美总结（数组、链表、栈、队列、递归、排序及二分）

---

title: 数据结构与算法之美总结（数组、链表、栈、队列、递归、排序及二分）
date: 2023-04-15 01:41:26
tags:

• 数据结构
• 算法
  categories:
• 数据结构与算法
  cover: https://cover.png
  feature: false

---

1. 前言

1、什么是数据结构？什么是算法？

• 从广义上讲，数据结构就是指一组数据的存储结构。算法就是操作数据的一组方法
• 从狭义上讲，是指某些著名的数据结构和算法，比如队列、栈、堆、二分查找、动态规划等。这些都是前人智慧的结晶，可以直接拿来用。这些经典数据结构和算法，都是前人从很多实际操作场景中抽象出来的，经过非常多的求证和检验，可以高效地帮助我们解决很多实际的开发问题

2、数据结构和算法有什么关系呢？

数据结构是为算法服务的，算法要作用在特定的数据结构之上。 因此，我们无法孤立数据结构来讲算法，也无法孤立算法来讲数据结构

比如，因为数组具有随机访问的特点，常用的二分查找算法需要用数组来存储数据。但如果选择链表这种数据结构，二分查找算法就无法工作了，因为链表并不支持随机访问

数据结构是静态的，它只是组织数据的一种方式。如果不在它的基础上操作、构建算法，孤立存在的数据结构就是没用的

大部分数据结构和算法知识点如下图所示：

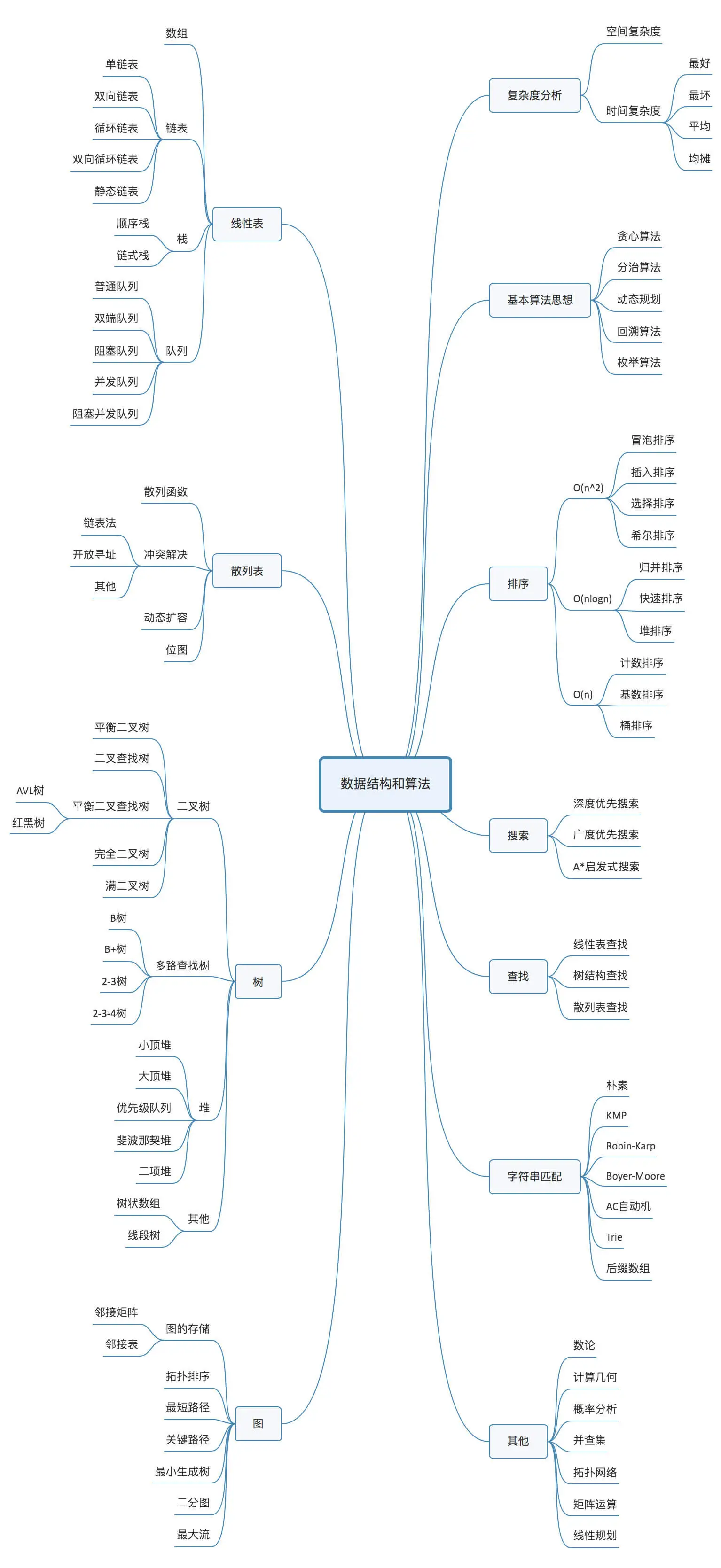
这里面有

• 10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
• 10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法

掌握了这些基础的数据结构和算法，再学更加复杂的数据结构和算法，就会非常容易、非常快

2. 复杂度分析

La estructura de datos y el algoritmo en sí resuelven el problema de "rápido" y "ahorro", es decir, cómo hacer que el código se ejecute más rápido y cómo hacer que el código ahorre espacio de almacenamiento. Por lo tanto, la eficiencia de ejecución es una consideración muy importante para el algoritmo. Entonces, ¿cómo medir la eficiencia de ejecución del código del algoritmo que escribe? Aquí se utiliza el análisis de complejidad de tiempo y espacio.

2.1 ¿Por qué es necesario el análisis de complejidad?

Puede estar un poco confundido, ejecute el código una vez y, a través de estadísticas y monitoreo, puede obtener el tiempo de ejecución del algoritmo y el tamaño de memoria que ocupa. ¿Por qué hacer análisis de complejidad de tiempo y espacio? ¿Puede este método de análisis ser más preciso que los datos obtenidos al volver a ejecutarlo?

En primer lugar, es seguro decir que este método de evaluación de la eficiencia de la ejecución del algoritmo es correcto. Muchos libros de estructuras de datos y algoritmos también le dieron un nombre a este método, llamado estadísticas post hoc . Sin embargo, este método estadístico tiene limitaciones muy grandes.

1. Los resultados de la prueba dependen mucho del entorno de prueba.

La diferencia de hardware en el entorno de prueba tendrá un gran impacto en los resultados de la prueba. Por ejemplo, tome el mismo fragmento de código y ejecútelo con un procesador Intel Core i9 y un procesador Intel Core i3. No hace falta decir que el procesador i9 se ejecuta mucho más rápido que el procesador i3. Además, por ejemplo, la velocidad de ejecución del código a en esta máquina es más rápida que la del código b, y cuando se cambia a otra máquina, puede haber resultados completamente opuestos.

2. Los resultados de las pruebas se ven muy afectados por el tamaño de los datos

Para el mismo algoritmo de ordenación, el grado de ordenación de los datos a ordenar es diferente y el tiempo de ejecución de la ordenación será muy diferente. En casos extremos, si los datos ya están en orden, el algoritmo de clasificación no necesita hacer nada y el tiempo de ejecución será muy corto. Además, si la escala de datos de prueba es demasiado pequeña, es posible que los resultados de la prueba no reflejen realmente el rendimiento del algoritmo. Por ejemplo, para la clasificación de datos a pequeña escala, la clasificación por inserción puede ser más rápida que la clasificación rápida.

Por lo tanto, necesitamos un método que pueda estimar aproximadamente la eficiencia de ejecución del algoritmo sin usar datos de prueba específicos para probar . Este es el método de análisis de complejidad de tiempo y espacio.

2.2 Notación de complejidad Big O

La eficiencia de ejecución de un algoritmo, en términos generales, es el tiempo de ejecución del código del algoritmo. Pero, ¿cómo obtener el tiempo de ejecución de un código a simple vista sin ejecutar el código?

Aquí hay un código muy simple para encontrar $1,2,3,4...\; La\; suma\; acumulada\; den$ , ahora, calculemos el tiempo de ejecución de este código

int cal(int n) {
    
    
    int sum = 0;
    int i = 1;
    for (; i <= n; ++i) {
    
    
        sum = sum + i;
    }
    return sum;
}

Desde la perspectiva de la CPU, cada línea de este código realiza una operación similar: leer datos-operar-escribir datos. Aunque el número de ejecuciones de CPU y el tiempo de ejecución correspondiente a cada línea de código son diferentes, esto es solo una estimación aproximada, por lo que se puede suponer que el tiempo de ejecución de cada línea de código es el mismo, que es unit_time. Según esta suposición, ¿cuál es el tiempo total de ejecución de este código?

Las líneas de código 2 y 3 requieren 1 tiempo de ejecución unit_time respectivamente, y las líneas 4 y 5 se ejecutan n veces, por lo que se necesitan $2norte\ast unit\_time$ tiempo de ejecución, por lo que el tiempo total de ejecución de este código es$(2norte+2)\ast unit\_time$ .$\_$$\_$$\_$Se puede ver que el tiempo de ejecución de todos los códigos es$T_{(n}$Proporcional al número de ejecuciones por línea de código

De acuerdo con esta idea de análisis, mire este código nuevamente

int cal(int n) {
    
    
    int sum = 0;
    int i = 1;
    int j = 1;
    for (; i <= n; ++i) {
    
    
        j = 1;
        for (; j <= n; ++j) {
    
    
            sum = sum + i * j;
        }
    }
}

Todavía se supone que el tiempo de ejecución de cada declaración es unit_time. Entonces el tiempo total de ejecución de este código $T_{(n}$¿Cuánto cuesta?

Cada una de las líneas de código 2, 3 y 4 requiere 1 unidad de tiempo para ejecutarse, y las líneas de código 5 y 6 se ejecutan n veces, lo que requiere $2norte\ast El\; tiempo\; de\; ejecución\; de\; unit\_time$ , las líneas 7 y 8 del bucle de código ejecutado$n$${norte}^2$ veces, entonces necesitamos$2{norte}^2\ast unit\_timetiempodeejecución$ .$\_$Por lo tanto, el tiempo total de ejecución de todo el código$T_{(n}=(2{norte}^2+2norte+3)\ast unit\_tiempo\_\_$

Aunque no se conoce el valor específico de unit_time, se puede obtener una regla muy importante mediante el proceso de derivación del tiempo de ejecución de estos dos códigos, es decir, el tiempo de ejecución T(n) de todos los códigos es proporcional a los tiempos de ejecución n de cada línea de código

Resume esta ley en una fórmula: $T_{(n}=O\left(f_{(n}\right)$

Entre ellos, $T_{\left(n \right)} $ representa el tiempo de ejecución del código; n representa el tamaño de la escala de datos; f ( n ) f_{\left(n \right $F_{(n}$Indica la suma del número de veces que se ejecuta cada línea de código. Como esta es una fórmula, usa $F_{(n}$Representar. O en la fórmula significa el tiempo de ejecución del código $T_{\left(n \right)} $ y $F_{(n}$La expresión es proporcional a

Entonces, T ( n ) = O ( 2 n + 2 ) T_{\left(n \right)} = O{(2n+2)} en el primer ejemplo$T_{(n}=O(2n\_+2)$ , T ( n ) = O ( 2 n 2 + 2 n + 3 ) T_{\left(n \right)} = O{(2n^2 + 2n + 3)} en el segundoejemplo$T_{(n}=O(2n{\_}^2+2norte+3)$ . Esta es la notación de complejidad de tiempo de Big O. La complejidad temporal de Big O en realidad no representa específicamente el tiempo de ejecución real del código, pero representa la tendencia de cambio del tiempo de ejecución del código con el crecimiento de la escala de datos, por lo que también se denomina complejidad temporal asintótica o complejidad temporal para abreviar.

Cuando n es grande, puedes considerarlo como 10000, 100000. Sin embargo, las partes de bajo nivel, constante y coeficiente de la fórmula no afectan la tendencia de crecimiento, por lo que pueden ignorarse. Solo necesita registrar una magnitud máxima. Si usa la notación O grande para expresar la complejidad temporal de las dos piezas de código que acabamos de mencionar, se puede registrar como: T ( n ) = O ( n ) T_{\left(n \right)} = O(n $T_{(n}=O\left(norte\right)$；$T_{(n}=O\left(n^2\right)$

2.3 Análisis de la Complejidad del Tiempo

El origen y la representación de la complejidad temporal de Big O se introdujeron anteriormente. Ahora veamos, ¿cómo analizar la complejidad temporal de una pieza de código?

1. Solo preste atención al código con la mayor cantidad de tiempos de ejecución de bucle

El método de representación de complejidad de Big O es solo una tendencia de cambio. Por lo general, las constantes, el orden bajo y los coeficientes en la fórmula se ignoran y solo se necesita registrar la magnitud del orden más grande. Por lo tanto, al analizar la complejidad temporal de un algoritmo o una pieza de código, solo preste atención a la pieza de código con la mayor cantidad de tiempos de ejecución de bucle. La magnitud de n en la cantidad de veces que se ejecuta este código central es la complejidad temporal de todo el código que se analizará

Como el ejemplo anterior:

int cal(int n) {
    
    
    int sum = 0;
    int i = 1;
    for (; i <= n; ++i) {
    
    
        sum = sum + i;
    }
    return sum;
}

La segunda y tercera líneas de código son tiempo de ejecución de nivel constante, que no tiene nada que ver con el tamaño de n, por lo que no tiene efecto sobre la complejidad. Los códigos en las líneas 4 y 5 son los que tienen más tiempos de ejecución de bucle, por lo que este fragmento de código debe analizarse enfáticamente. Estas dos líneas de código se ejecutan n veces, por lo que la complejidad de tiempo total es $O\left(n\right)$

2. Regla de la suma: la complejidad total es igual a la complejidad del código de mayor magnitud

Por ejemplo:

int cal(int n) {
    
    
    int sum_1 = 0;
    int p = 1;
    for (; p < 100; ++p) {
    
    
        sum_1 = sum_1 + p;
    }
    int sum_2 = 0;
    int q = 1;
    for (; q < n; ++q) {
    
    
        sum_2 = sum_2 + q;
    }
    int sum_3 = 0;
    int i = 1;
    int j = 1;
    for (; i <= n; ++i) {
    
    
        j = 1;
        for (; j <= n; ++j) {
    
    
            sum_3 = sum_3 + i * j;
        }
    }
    return sum_1 + sum_2 + sum_3;
}

Este código se divide en tres partes, a saber, sum_1, sum_2, sum_3. Puede analizar la complejidad temporal de cada parte por separado, luego juntarlas y luego tomar la de mayor magnitud como la complejidad de todo el código.

¿Cuál es la complejidad temporal del primer período? Este bucle de código se ejecuta 100 veces, por lo que es un tiempo de ejecución constante, que no tiene nada que ver con el tamaño de n

Aquí nuevamente, incluso si este código se repite 10 000 o 100 000 veces, siempre que sea un número conocido, independientemente de n, sigue siendo un tiempo de ejecución constante. Cuando n es infinito, se puede ignorar. Aunque tendrá un gran impacto en el tiempo de ejecución del código, volviendo al concepto de complejidad del tiempo, representa la tendencia de cambio de la eficiencia de ejecución de un algoritmo y el crecimiento de la escala de datos, por lo que no importa cuánto tiempo sea el tiempo de ejecución constante, puede ignorarse. Porque no tiene ningún efecto sobre la tendencia de crecimiento por sí mismo.

¿Cuál es la complejidad temporal de la segunda pieza de código y la tercera pieza de código? La respuesta es $O\left(n\right)$ Suma$O\left(n^2\right)$, debería ser fácil de analizar, se combina la complejidad temporal de estas tres piezas de código y se toma el orden de magnitud más grande. Por lo tanto, la complejidad temporal de todo el código es$O\left(n\right)$ . Es decir: la complejidad temporal total es igual a la complejidad temporal del código de mayor magnitud. Luego abstraiga esta regla en una fórmula:

如果$T{1}_{(n}=O(f_{(n})$，$T{2}_{\left(n\right)}=O(g_{\left(n\right)})$。那么 $T_{\left(n\right)}=T{1}_{\left(n\right)}+T{2}_{\left(n\right)}=max(O(f_{\left(n\right)}),O(g_{\left(n\right)})=O(max(O(f_{\left(n\right)}),O(g_{\left(n\right)})))$

3、乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

类比上面的加法法则，如果 $T{1}_{\left(n\right)}=O(f_{\left(n\right)})$，$T{2}_{\left(n\right)}=O(g_{\left(n\right)})$。那么 $T_{\left(n\right)}=T{1}_{\left(n\right)}\ast T{2}_{\left(n\right)}=O(f_{\left(n\right)})\ast O(g_{\left(n\right)})=O(f_{\left(n\right)}\ast g_{\left(n\right)})$

也就是说，假设如果 $T{1}_{\left(n\right)}=O\left(norte\right)$ ,$T2{\_}_{(n}=O\left(n^2\right)$，则$T{1}_{(n}\ast T2{\_}_{(n}=O\left(n^3\right)$

Para implementar el código específico, la regla de multiplicación se puede considerar como un bucle anidado, como en el siguiente ejemplo:

int cal(int n) {
    
    
    int ret = 0;
    int i = 1;
    for (; i < n; ++i) {
    
    
        ret = ret + f(i);
    }
}
int f(int n) {
    
    
    int sum = 0;
    int i = 1;
    for (; i < n; ++i) {
    
    
        sum = sum + i;
    }
    return sum;
}

Véase cal()función sola. Asumiendo que f()es solo una operación ordinaria, la complejidad temporal de las líneas 4~6 es, $T{1}_{(n}=O\left(n\right)$ . Perof()la función en sí no es una operación simple, su complejidad temporal es$T2{\_}_{(n}=O\left(n\right)$ , entonces,cal()la complejidad temporal de toda la función es,$T{1}_{(n}\ast T2{\_}_{(n}=O\left(n\right)\ast O\left(n\right)=O\left(n^2\right)$

2.4 Análisis de varios ejemplos comunes de complejidad de tiempo

Las escalas de complejidad comunes son las siguientes:

• Orden constante: $O\left(1\right)$
• Orden logarítmico: $O\left(iniciarsesión\right)\_\_$
• Orden lineal: $O\left(n\right)$
• Orden logarítmico lineal: $O\left(nlogn\right)\_\_$
• Orden cuadrático: $O\left(n^2\right)$
• Orden cúbico: $O\left(n^3\right)$
• orden k: $O\left(n^k\right)$
• Orden exponencial: $O\left(2^{norte}\right)$
• Paso factorial: $O(n!)$

Para la escala compleja enumerada anteriormente, se puede dividir aproximadamente en dos categorías, escala polinómica y escala no polinómica. Entre ellos, solo hay dos magnitudes no polinómicas: $O\left(2^n\right)$suma$O(n!)$

Cuando el tamaño de los datos n aumenta, el tiempo de ejecución de los algoritmos de nivel no polinomial aumentará considerablemente y el tiempo de ejecución de la resolución de problemas aumentará infinitamente. Por lo tanto, los algoritmos con complejidad temporal no polinomial son en realidad algoritmos muy ineficientes.

1, $O\left(1\right)$

Primero se debe aclarar un concepto, $O\left(1\right)$ es solo una representación de la complejidad de tiempo de nivel constante, no que solo se ejecute una línea de código. Por ejemplo, este código, incluso con 3 líneas, su complejidad temporal es$O\left(1\right)$ en lugar de$O\left(3\right)$

int i = 8;
int j = 6;
int sum = i + j;

Siempre que el tiempo de ejecución del código no aumente con el aumento de n, la complejidad temporal del código se registra como $O\left(1\right)$ . En otras palabras, en general, siempre que no haya declaraciones de bucle o recursivas en el algoritmo, incluso si hay miles de líneas de código, la complejidad del tiempo es$O\left(1\right)$

2、$O\left(iniciarsesión\right)、$ O (iniciar sesión) O (iniciar$sesión$ )$O\left(nlogn\right)\_\_$

La complejidad de tiempo logarítmica es muy común, y también es la complejidad de tiempo más difícil de analizar, como en el siguiente ejemplo:

i = 1;
while (i <= n) {
    
    
    i = i * 2;
}

De acuerdo con el método de análisis de complejidad mencionado anteriormente, la tercera línea de código es el ciclo que se ejecuta con mayor frecuencia. Por lo tanto, siempre que pueda calcular cuántas veces se ejecuta esta línea de código, puede conocer la complejidad temporal de todo el código.

Se puede ver en el código que el valor de la variable i comienza desde 1 y se multiplica por 2 en cada ciclo. Cuando es mayor que n, el ciclo termina. De hecho, el valor de la variable i es una sucesión geométrica. Si los enumera uno por uno, debería verse así: $2^{0}2{}^{1}2{}^2...2{}^X=norte$

Entonces, siempre que conozca el valor de x, sabrá la cantidad de veces que se ejecuta esta línea de código. por $2^X=n$ Resolviendo x Este problema se debe aprender en la escuela secundaria,$X=registro\_{\_}_{}n$ , por lo que la complejidad temporal de este código es$O(log\_{\_}_{}norte)$

Ahora, cambie un poco el código y vea, ¿cuál es la complejidad temporal de este código?

i = 1;
while (i <= n) {
    
    
    i = i * 3;
}

De acuerdo con la idea que acabamos de mencionar, es fácil ver que la complejidad temporal de este código es $O(log\_{\_}_{}norte)$

De hecho, independientemente de la base 2, la base 3 o la base 10, la complejidad temporal de todos los órdenes logarítmicos se puede registrar como $O(iniciar\; sesiónn)$ .$\_$$\_$¿por qué?

Los logaritmos se pueden convertir entre sí, según la fórmula:

$$registro\_{\_}_{}b=\frac{registro\_{\_}_{}}{registro\_{\_}_{}a}$$

Disponible $registro\_{\_}_{}norte=\frac{registro\_{\_}_{}}{registro\_{\_}_{}2}$. Entonces $registro\_{\_}_{}n$ es igual a$registro\_{\_}_{}2\ast registro\_{\_}_{}n$ , porque$O(log\_{\_}_{}norte)=O(C\ast registro\_{\_}_{}n)$ , donde$C=registro\_{\_}_{}2$ es una constante. Basado en una teoría anterior: Al usar O grande para marcar la complejidad, se puede ignorar el coeficiente, es decir,$O\left(C{f}_{(n}\right)=O\left(f_{(n}\right)$ . Entonces,$O(log\_{\_}_{}n)$ es igual a$O(log\_{\_}_{}n)$ . Por lo tanto, en el método de expresión de la complejidad del tiempo logarítmico, la "base" del logaritmo se ignora y se expresa uniformemente como$O\left(iniciarsesión\right)\_\_$

Si entiende el O (logn) O (log n) mencionado anteriormente$O\left(iniciarsesión\right),$ NO$(iniciar\; sesión)\; O\; ($$O\left(nlogn\right)es$ fácil de entender$.$Si la complejidad temporal de un fragmento de código es$O\left(logn\right)$ , ejecuta el ciclo n veces, la complejidad del tiempo es$O$$($$nlogn$$O\left(nlogn\right)también$ .$\_$Además,$O\left(nlogn\right)es\; también\; una\; complejidadde\; tiempo$ de algoritmo muy común . Por ejemplo, la complejidad temporal de la ordenación por fusión y la ordenación rápida es$O\left(nlogn\right)\_\_$

3、$O(m+norte)$、$O(m\ast norte)$

Hablamos de una complejidad temporal diferente a la anterior, la complejidad del código está determinada por el tamaño de los dos datos, como se muestra en el siguiente ejemplo:

int cal(int m, int n) {
    
    
    int sum_1 = 0;
    int i = 1;
    for (; i < m; ++i) {
    
    
        sum_1 = sum_1 + i;
    }
    int sum_2 = 0;
    int j = 1;
    for (; j < n; ++j) {
    
    
        sum_2 = sum_2 + j;
    }
    return sum_1 + sum_2;
}

Como puede verse en el código, m y n representan dos escalas de datos. Es imposible evaluar de antemano cuál de m y n tiene una magnitud mayor, por lo que al expresar complejidad, uno no puede simplemente usar la regla de la suma y omitir uno de ellos. Entonces, la complejidad temporal del código anterior es $O(m+norte)$

En este caso, la regla de la suma original es incorrecta y la regla de la suma debe cambiarse a: $T{1}_{(m}+T2{\_}_{(n}=O(f_{(n}+{gramo}_{(n})$ . Pero la regla de la multiplicación continúa:$T{1}_{(m}\ast T2{\_}_{(n}=O(f_{(n}\ast {gramo}_{(n})$

2.5 Análisis de la complejidad del espacio

Después de comprender el análisis de la complejidad del tiempo mencionado anteriormente, el método de análisis de la complejidad del espacio es muy sencillo de aprender.

El nombre completo de complejidad temporal es complejidad temporal asintótica, lo que significa la relación de crecimiento entre el tiempo de ejecución del algoritmo y el tamaño de los datos . Por analogía, el nombre completo de complejidad espacial es complejidad espacial asintótica (complejidad espacial asintótica), que representa la relación de crecimiento entre el espacio de almacenamiento del algoritmo y la escala de datos.

El siguiente ejemplo (generalmente nadie escribirá así, aquí es para facilitar la explicación)

void print(int n) {
    
    
    int i = 0;
    int[] a = new int[n];
    for (i; i < n; ++i) {
    
    
        a[i] = i * i;
    }
    for (i = n - 1; i >= 0; --i) {
    
    
        print out a[i]
    }
}

Similar al análisis de la complejidad del tiempo, podemos ver que en la segunda línea de código, se aplica una variable de almacenamiento de espacio i, pero es de orden constante y no tiene nada que ver con el tamaño de los datos n, por lo que puede ignorarse. La línea 3 aplica para una matriz de tipo int con tamaño n, aparte de eso, el resto del código no ocupa más espacio, por lo que la complejidad espacial de todo el código es O ( n ) O(n $O\left(n\right)$

La complejidad del espacio común es $O\left(1\right)$、$O\left(norte\right)$ ,$O\left(n^2\right)$, la imagen$O\left(iniciarsesión\right)、$ O (iniciar sesión) O (iniciar$sesión$ )$La\; complejidad\; logarítmica$ como$O$$($$n$$log$$n$$)\; generalmente$$no\; se\; usa.$Además, el análisis de la complejidad del espacio es mucho más simple que el análisis de la complejidad del tiempo.

2.6 Complejidad de tiempo de caso promedio mejor, peor y promedio

Veamos primero un ejemplo:

// n 表示数组 array 的长度
int find(int[] array, int n, int x) {
    
    
    int i = 0;
    int pos = -1;
    for (; i < n; ++i) {
    
    
        if (array[i] == x) pos = i;
    }
    return pos;
}

La función de este código es encontrar la posición donde aparece la variable x en un arreglo desordenado (array). Si no se encuentra, se devuelve -1. Según el método de análisis mencionado anteriormente, la complejidad de este código es $O\left(n\right)$ donde n es la longitud de la matriz

Para encontrar una parte de los datos en una matriz, no es necesario recorrer toda la matriz cada vez, porque es posible finalizar el bucle antes de tiempo si se encuentra a la mitad. Sin embargo, este código no está escrito de manera suficientemente eficiente. Puede optimizar este código de búsqueda de esta manera:

// n 表示数组 array 的长度
int find(int[] array, int n, int x) {
    
    
    int i = 0;
    int pos = -1;
    for (; i < n; ++i) {
    
    
        if (array[i] == x) {
    
    
            pos = i;
            break;
        }
    }
    return pos;
}

这个时候，问题就来了。优化完之后，这段代码的时间复杂度还是 $O(n)$ 吗？很显然，前面讲的分析方法，解决不了这个问题

因为，要查找的变量 x 可能出现在数组的任意位置。如果数组中第一个元素正好是要查找的变量 x，那就不需要继续遍历剩下的 n-1 个数据了，那时间复杂度就是 $O(1)$。但如果数组中不存在变量 x，那就需要把整个数组都遍历一遍，时间复杂度就成了 $O(n)$。所以，不同的情况下，这段代码的时间复杂度是不一样的

为了表示代码在不同情况下的不同时间复杂度，需要引入三个概念：最好情况时间复杂度（best case time complexity）、最坏情况时间复杂度（worst case time complexity）和平均情况时间复杂度（average case time complexity）

• 顾名思义，最好情况时间复杂度就是，在最理想的情况下，执行这段代码的时间复杂度。就像刚刚讲到的，在最理想的情况下，要查找的变量 x 正好是数组的第一个元素，这个时候对应的时间复杂度就是最好情况时间复杂度
• 同理，最坏情况时间复杂度就是，在最糟糕的情况下，执行这段代码的时间复杂度。就像刚举的那个例子，如果数组中没有要查找的变量 x，需要把整个数组都遍历一遍才行，所以这种最糟糕情况下对应的时间复杂度就是最坏情况时间复杂度

La complejidad de tiempo del mejor de los casos y la complejidad del tiempo del peor de los casos corresponden a la complejidad del código en casos extremos, y la probabilidad de ocurrencia en realidad no es alta. Para representar mejor la complejidad del caso promedio, es necesario introducir otro concepto: la complejidad temporal promedio del caso, en lo sucesivo denominada complejidad temporal promedio.

¿Cómo analizar la complejidad del tiempo promedio? Todavía usando el ejemplo de encontrar la variable x justo ahora

La posición de la variable x que se encuentra en el arreglo tiene n+1 casos: está en la posición 0～n-1 del arreglo y no está en el arreglo. En cada caso, sume el número de elementos que se deben recorrer y luego divida por n+1 para obtener el número promedio de elementos que se deben recorrer. La fórmula es la siguiente (la suma de la secuencia aritmética es igual al primer elemento más el último elemento multiplicado por el número de elementos dividido por 2):

$$\frac{1+2+3+...+norte+}{norte+1}=\frac{(1+norte)\times \frac{}{2}+}{norte+1}=\frac{\frac{norte+{norte}^2+2n}{2}}{norte+1}=\frac{norte\_\_+3}{2(n+1)}$$

En la notación O grande de la complejidad del tiempo, se pueden omitir los coeficientes, los órdenes bajos y las constantes. Por lo tanto, después de simplificar la fórmula anterior, la complejidad del tiempo promedio obtenida es O ( n ) O(n $O\left(n\right)$

Aunque esta conclusión es correcta, el proceso de cálculo es ligeramente problemático. ¿Cuál es el problema? Las n+1 situaciones mencionadas anteriormente tienen diferentes probabilidades

La variable x que se va a buscar está en la matriz o no está en la matriz. La probabilidad correspondiente a estas dos situaciones es engorrosa de contar. Para facilitar la comprensión, se supone que la probabilidad de estar en el arreglo y no estar en el arreglo es 1/2. Además, la probabilidad de que los datos a buscar aparezcan en las n posiciones de 0 a n-1 es la misma, que es 1/n. Por lo tanto, según la regla de la multiplicación de probabilidades, la probabilidad de que los datos a buscar aparezcan en cualquier posición entre 0 y n-1 es $\frac{}{2norte}$

Por lo tanto, el mayor problema en el proceso de derivación anterior es que no se tiene en cuenta la probabilidad de ocurrencia de varias situaciones. Si además se tiene en cuenta la probabilidad de ocurrencia de cada situación, el proceso de cálculo de la complejidad temporal media queda así:

$$1\times \frac{}{2norte}+2\times \frac{}{2norte}+3\times \frac{}{2norte}+...+norte\times \frac{}{2norte}+norte\times \frac{}{2}=((1+norte)\times \frac{}{2})\times \frac{}{2norte}+\frac{}{2}=\frac{norte+{norte}^{}}{4norte}+\frac{}{2}=\frac{3norte+}{4}$$

Este valor es el promedio ponderado en la teoría de la probabilidad , también conocido como valor esperado , por lo que el nombre completo de complejidad de tiempo promedio debe llamarse complejidad de tiempo promedio ponderado o complejidad de tiempo esperado

Después de introducir la probabilidad, el promedio ponderado del código anterior es $\frac{3n+}{4}$. Expresado en notación O grande, la complejidad temporal media ponderada de este código sigue siendo $O\left(n\right)$

De hecho, en la mayoría de los casos, no hay necesidad de distinguir entre las complejidades de tiempo del caso mejor, peor y promedio. En muchos casos, el uso de una complejidad puede satisfacer las necesidades. Solo cuando la misma pieza de código tiene una diferencia de orden de magnitud en la complejidad del tiempo en diferentes circunstancias, estas tres representaciones de complejidad se utilizarán para distinguir

2.7 Complejidad del tiempo amortizado

Complejidad de tiempo, suena un poco como la complejidad de tiempo promedio. Como se mencionó anteriormente, en la mayoría de los casos, no es necesario distinguir entre la mejor, la peor y la complejidad promedio. La complejidad promedio solo se usa en algunos casos especiales, y los escenarios de aplicación de la complejidad del tiempo amortizado son más especiales y más limitados que ella, como en el siguiente ejemplo (solo por conveniencia de explicación, generalmente nadie lo escribirá así):

// array 表示一个长度为 n 的数组
// 代码中的 array.length 就等于 n
int[] array = new int[n];
int count = 0;
void insert(int val) {
    
    
    if (count == array.length) {
    
    
        int sum = 0;
        for (int i = 0; i < array.length; ++i) {
    
    
            sum = sum + array[i];
        }
        array[0] = sum;
        count = 1;
    }
    array[count] = val;
    ++count;
}

Este código implementa una función para insertar datos en una matriz. Cuando la matriz está llena, es decir, en el código count == array.length, use el ciclo for para atravesar la matriz para sumar y borrar la matriz, coloque el valor de la suma después de la suma en la primera posición de la matriz y luego inserte nuevos datos. Pero si la matriz tiene espacio libre al principio, inserte los datos directamente en la matriz.

¿Cuál es la complejidad temporal de este código?

En el caso más ideal, hay espacio libre en la matriz, y solo es necesario insertar los datos en la posición donde se cuenta el subíndice de la matriz, por lo que la complejidad del tiempo es $ O(1) $ en el mejor de los casos. En el peor de los casos, no hay espacio libre en la matriz, y la matriz debe recorrerse y sumarse primero, y luego se insertan los datos, por lo que la complejidad del tiempo en el peor de los casos es O ( n ) O(n $O\left(n\right)$

¿Cuál es la complejidad del tiempo promedio? La respuesta es $O\left(1\right)$ . Todavía se puede analizar a través del método de la teoría de la probabilidad mencionado anteriormente.

Suponiendo que la longitud de la matriz es n, según la posición de inserción de datos, se puede dividir en n casos, y la complejidad temporal de cada caso es O ( 1 ) $O\left(1\right)$ . Además, existe una situación "extra", que consiste en insertar un dato cuando no hay espacio libre en la matriz. La complejidad temporal en este momento es$O\left(n\right)$ . Además, la probabilidad de estas n+1 situaciones es la misma, todas son$\frac{}{norte+1}$. Por tanto, según el método de cálculo de la media ponderada, la complejidad temporal media obtenida es:

$$1\times \frac{}{norte+1}+1\times \frac{}{norte+1}+...+norte\times \frac{}{norte+1}=O\left(1\right)$$

Pero el análisis de complejidad promedio en este ejemplo no necesita ser tan complicado y no necesita introducir el conocimiento de la teoría de la probabilidad. ¿Por qué es esto? Primero comparemos este insert()ejemplo con el ejemplo anterior find(), encontrará que hay una gran diferencia entre los dos.

• En primer lugar, find()la complejidad de la función es $O\left(1\right)$ . Peroinsert()en la mayoría de los casos, la complejidad del tiempo es$O\left(1\right)$ . Solo en unos pocos casos, la complejidad es relativamente alta,$O\left(n\right)$
• Para insert()la función, $O\left(1\right)$ complejidad de tiempo para inserción y$La\; inserción\; de\; la\; complejidad\; del\; tiempo\; O\left(n\right)$ , la frecuencia de ocurrencia es muy regular, y existe una cierta relación de tiempo antes y después, generalmente un$Inserción\; O\left(n\right)$ seguida de n-1$O\left(1\right)$ operación de inserción, itera una y otra vez

Por lo tanto, para el análisis de complejidad de una escena tan especial, no es necesario averiguar todas las situaciones de entrada y las probabilidades de ocurrencia correspondientes como en el método de análisis de complejidad promedio anterior, y luego calcular el promedio ponderado

Para este escenario especial, se introduce un método de análisis más simple: el método de análisis amortizado La complejidad temporal obtenida a través del análisis amortizado se denomina complejidad temporal amortizada

Entonces, ¿cómo utilizar el método de análisis amortizado para analizar la complejidad del tiempo amortizado del algoritmo?

Mire el ejemplo anterior de insertar datos en la matriz, cada vez que $Las\; operaciones\; de\; inserción\; O\left(n\right)$ serán seguidas por n-1 veces$O\left(1\right)$ operación de inserción, por lo que la operación que consume más tiempo se distribuye uniformemente a las siguientes n-1 operaciones que consumen menos tiempo, y la complejidad de tiempo promedio de este grupo de operaciones continuas es O ( 1 ) O(1$O\left(1\right)$ . Esta es la idea general del análisis amortizado

Los escenarios de aplicación de la complejidad del tiempo amortizado y el análisis amortizado son relativamente especiales, por lo que no se utilizan con frecuencia.

En un grupo de operaciones continuas en una estructura de datos, la complejidad de tiempo es muy baja en la mayoría de los casos. Solo en algunos casos, la complejidad de tiempo es relativamente alta, y existe una relación de tiempo coherente entre estas operaciones. En este momento, este grupo de operaciones se puede analizar en conjunto para ver si el consumo de tiempo de la operación con mayor complejidad de tiempo se puede amortizar con otras operaciones con menor complejidad de tiempo. Además, cuando se puede aplicar el análisis de la complejidad del tiempo amortizado, la complejidad del tiempo amortizado general es igual a la complejidad del tiempo en el mejor de los casos.

Aunque muchos libros de estructura de datos y algoritmos se han esforzado mucho en distinguir entre la complejidad de tiempo promedio y la complejidad de tiempo amortizado, de hecho, personalmente creo que la complejidad de tiempo amortizado es una complejidad de tiempo promedio especial, y no hay necesidad de esforzarse demasiado para distinguirlos. Lo más importante a dominar es su método de análisis, análisis de amortización. En cuanto a si el resultado del análisis se llama promedio o se comparte equitativamente, esto es solo una forma de decir que no es importante.

3. Matrices

3.1 ¿Cómo lograr el acceso aleatorio?

Array (Array) es una estructura de datos de tabla lineal. Utiliza un conjunto de espacios de memoria contiguos para almacenar un conjunto de datos del mismo tipo.

Hay varias palabras clave en esta definición Después de entender estas palabras clave, básicamente puede comprender el concepto de matrices a fondo.

1. Lista lineal

Como su nombre lo indica, una tabla lineal es una estructura en la que los datos se organizan como una línea. Los datos de cada tabla lineal tienen como máximo dos direcciones, adelante y atrás. De hecho, además de las matrices, las listas enlazadas, las colas, las pilas, etc. también son estructuras de tablas lineales.

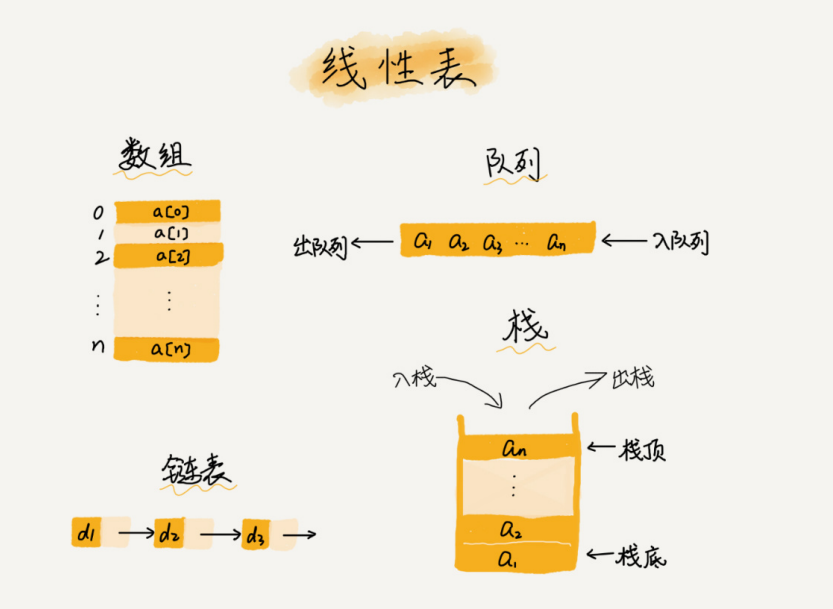
El concepto opuesto es una tabla no lineal, como un árbol binario, un montón, un gráfico, etc. La razón por la que se llama no lineal es que en una tabla no lineal, no hay un contexto simple entre los datos

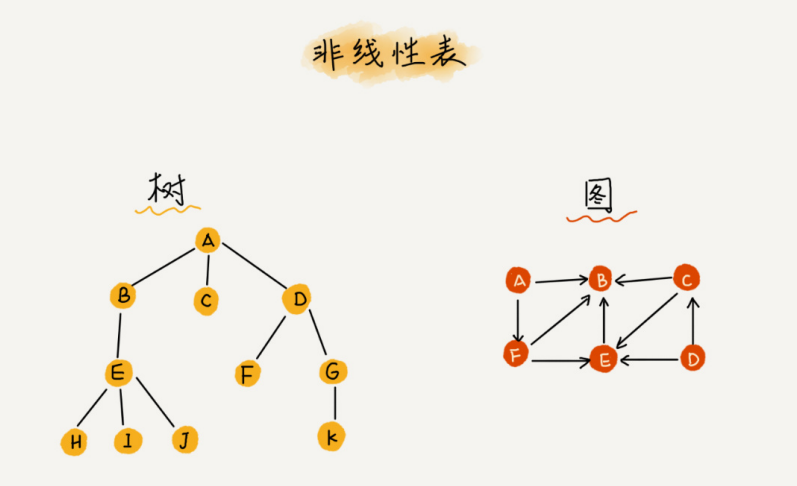
2. Espacio de memoria contiguo y el mismo tipo de datos

Es precisamente por estas dos limitaciones que tiene una función llamada "killer": "acceso aleatorio". Pero hay ventajas y desventajas. Estas dos limitaciones también hacen que muchas operaciones en la matriz sean muy ineficientes. Por ejemplo, si desea eliminar o insertar una parte de los datos en la matriz, para garantizar la continuidad, necesita mover una gran cantidad de datos.

¿Cómo implementa la matriz el acceso aleatorio a los elementos de la matriz en función de los subíndices?

Tome una matriz de tipo int con una longitud de 10 int[] a = new int[10]como ejemplo. En la figura a continuación, la computadora asigna un espacio de memoria continuo de 1000 a 1039 para la matriz a[10], donde la primera dirección del bloque de memoria es base_address = 1000

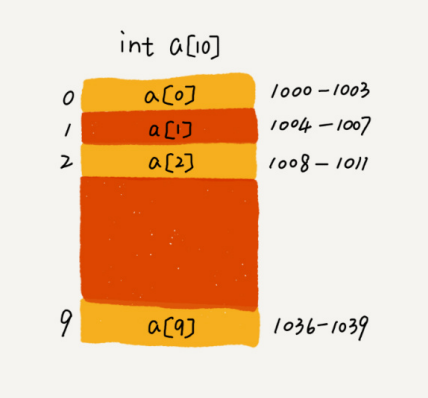
La computadora asigna una dirección a cada unidad de memoria, y la computadora usa la dirección para acceder a los datos en la memoria. Cuando la computadora necesita acceder aleatoriamente a un elemento en la matriz, primero calculará la dirección de memoria del elemento a través de la siguiente fórmula de direccionamiento:

a[i]_dirección = dirección_base + i * tamaño_tipo_datos

Donde data_type_size representa el tamaño de cada elemento en la matriz. En el ejemplo anterior, los datos de tipo int se almacenan en la matriz, por lo que data_type_size es bytes 4. Esta fórmula es muy simple, por lo que no introduciré demasiado aquí

Hay un "error" que corregir aquí. Durante las entrevistas, a menudo se pregunta la diferencia entre matrices y listas vinculadas, y muchas personas responden: "Las listas vinculadas son adecuadas para la inserción y eliminación, y la complejidad del tiempo es O ( 1 ) $O\left(1\right)$ ; la matriz es adecuada para la búsqueda, la complejidad del tiempo de búsqueda es$O\left(1\right)$ ”

De hecho, esta representación es inexacta. Las matrices son adecuadas para las operaciones de búsqueda, pero la complejidad temporal de la búsqueda no es $O\left(1\right)$ . Incluso para arreglos ordenados, usando búsqueda binaria, la complejidad del tiempo es$O(iniciar\; sesiónn)$ .$\_$$\_$Por lo tanto, la expresión correcta debería ser que la matriz admita el acceso aleatorio, y la complejidad temporal del acceso aleatorio según el subíndice es$O\left(1\right)$

3.2 "insertar" y "eliminar" ineficientes

Como se mencionó anteriormente, para mantener la continuidad de los datos de la memoria en la matriz, las dos operaciones de inserción y eliminación serán relativamente ineficientes. Ahora, ¿por qué exactamente esto está causando la ineficiencia? ¿Cuáles son las formas de mejorarlo?

Primer vistazo a la operación de inserción

Suponiendo que la longitud de la matriz es n, ahora, si es necesario insertar un dato en la posición k-ésima de la matriz. Para liberar la k-ésima posición para los nuevos datos, es necesario mover los elementos de la k-ésima a la n-ésima parte hacia atrás secuencialmente. ¿Cuál es la complejidad temporal de la operación de inserción?

Si inserta elementos al final de la matriz, no es necesario mover los datos y la complejidad del tiempo es $O\left(1\right)$ . Pero si inserta un elemento al comienzo de la matriz, todos los datos deben moverse hacia atrás uno por uno, por lo que la peor complejidad de tiempo es$O\left(n\right)$ . Debido a que la probabilidad de insertar un elemento en cada posición es la misma, la complejidad de tiempo de caso promedio es$\frac{1+2+...}{norte}=O\left(n\right)$

Si los datos en la matriz están ordenados, cuando se inserta un nuevo elemento en una determinada posición, los datos después de k deben moverse de acuerdo con el método de ahora. Sin embargo, si los datos almacenados en la matriz no tienen reglas, la matriz solo se considera una colección de datos almacenados. En este caso, si desea insertar una matriz en la posición k-ésima, para evitar el movimiento de datos a gran escala, existe otra forma sencilla de mover directamente el bit de datos k-ésimo al final del elemento de la matriz y colocar el nuevo elemento directamente en la posición k-ésima.

Por ejemplo, los siguientes 5 elementos se almacenan en la matriz a[10]: a, b, c, d, e. Ahora el elemento x debe insertarse en la tercera posición. Simplemente coloque c en a[5] y asigne a[2] a x. Finalmente, los elementos de la matriz son los siguientes: a, b, x, d, e, c

Utilizando esta técnica de procesamiento, en un escenario específico, la complejidad temporal de insertar un elemento en la posición k-ésima se reducirá a $O\left(1\right)$ . Esta idea de procesamiento también se utilizará en la clasificación rápida

Veamos la operación de eliminación.

Similar a la inserción de datos, si desea eliminar los datos en la k-ésima posición, también debe mover los datos para la continuidad de la memoria; de lo contrario, habrá un agujero en el medio y la memoria no será continua.

Similar a la inserción, si elimina los datos al final de la matriz, la complejidad de tiempo del mejor de los casos es $O\left(1\right)$ ; si elimina los datos al principio, la complejidad de tiempo en el peor de los casos es$O\left(n\right)$ ; la complejidad del tiempo de caso promedio también es$O\left(n\right)$

De hecho, en algunos escenarios especiales, no es necesario buscar la continuidad de los datos en la matriz. Si se realizan varias operaciones de eliminación juntas, ¿se mejorará mucho la eficiencia de la eliminación?

Por ejemplo, se almacenan 8 elementos en la matriz a[10]: a, b, c, d, e, f, g, h. Ahora, para eliminar a, b, c tres elementos a la vez

Para evitar que los datos de d, e, f, g y h se muevan tres veces, primero puede grabar los datos eliminados. Cada operación de eliminación en realidad no mueve los datos, sino que solo registra que los datos se han eliminado. Cuando la matriz no tiene más espacio para almacenar datos, se activa una operación de eliminación real, lo que reduce en gran medida el movimiento de datos causado por la operación de eliminación.

Si comprende la JVM, encontrará que esta es la idea central del algoritmo de recolección de basura de barrido de marcas de JVM. Este es el encanto de las estructuras de datos y los algoritmos. En muchos casos, no se trata de memorizar una determinada estructura de datos o algoritmo de memoria, sino aprender las habilidades de pensamiento y procesamiento que hay detrás. Estas cosas son las más valiosas. Si presta atención, ya sea en el desarrollo de software o en el diseño de la arquitectura, siempre puede encontrar la sombra de ciertos algoritmos y estructuras de datos.

3.3 Tenga cuidado con el acceso a la matriz fuera de los límites

Primero, analicemos los resultados de ejecución de este código de lenguaje C:

int main(int argc, char * argv[]) {
    
    
    int i = 0;
    int arr[3] = {
    
    0};
    for(; i <= 3; i++) {
    
    
        arr[i] = 0;
        printf("hello world\n");
    }
    return 0;
}

El resultado de este código no es imprimir tres líneas de "hola palabra", sino imprimir "hola mundo" infinitamente.¿Por qué?

Debido a que el tamaño de la matriz es 3, a[0], a[1], a[2], y el código está mal escrito, la condición final del bucle for está mal escrita como i<=3 en lugar de i<3, por lo que cuando i=3, el acceso de la matriz a[3] está fuera de los límites

En el lenguaje C, todos los espacios de memoria son de libre acceso siempre que no sean memoria de acceso restringido. De acuerdo con la fórmula de direccionamiento de matriz mencionada anteriormente, a[3] también se ubicará en una dirección de memoria que no pertenece a la matriz, y esta dirección resulta ser la dirección de memoria donde se almacena la variable i, entonces a[3]=0 es equivalente a i=0, por lo que conducirá a un bucle infinito de código

La matriz fuera de los límites es un comportamiento pendiente en el lenguaje C, y no existe una regulación sobre cómo el compilador debe manejar el acceso a la matriz fuera de los límites. Debido a que la esencia de acceder a una matriz es acceder a una parte de la memoria continua, siempre que la dirección de memoria obtenida al calcular el desplazamiento de la matriz esté disponible, es posible que el programa no informe ningún error.

En este caso, generalmente se producirán errores lógicos inexplicables.Al igual que en el ejemplo anterior, la depuración es muy difícil. Además, muchos virus informáticos también usan las lagunas en el código para acceder a direcciones ilegales cuando la matriz está fuera de los límites para atacar el sistema, por lo que al escribir código, debe tener cuidado con la matriz fuera de los límites.

Pero no todos los lenguajes son como C, lo que deja el trabajo de las comprobaciones fuera de los límites de la matriz a los programadores, ya que Java mismo hará comprobaciones fuera de los límites, como las siguientes líneas de código Java, arrojarájava.lang.ArrayIndexOutOfBoundsException

int[] a = new int[3];
a[3] = 10;

3.4 ¿Pueden los contenedores reemplazar completamente los arreglos?

Para los tipos de matrices, muchos lenguajes ofrecen clases de contenedor, como ArrayList en Java y vector en C++ STL. En el desarrollo de proyectos, ¿cuándo es apropiado usar arreglos y cuándo es apropiado usar contenedores?

Tome el lenguaje Java como ejemplo. Si es ingeniero de Java y usa ArrayList casi todos los días, debe estar muy familiarizado con él. Entonces, ¿qué ventajas tiene sobre las matrices?

Personalmente, la mayor ventaja de ArrayList es que puede encapsular los detalles de muchas operaciones de matriz. Por ejemplo, al insertar y eliminar datos en la matriz mencionada anteriormente, es necesario mover otros datos. Además, tiene otra ventaja, es decir, admite la expansión dinámica.

La matriz en sí necesita especificar el tamaño por adelantado cuando se define, porque necesita asignar espacio de memoria continuo. Si solicita una matriz con un tamaño de 10, cuando los datos 11 deben almacenarse en la matriz, debe reasignar un espacio más grande, copiar los datos originales y luego insertar los nuevos datos.

Si usa ArrayList, no necesita preocuparse en absoluto por la lógica de expansión subyacente, ya que ArrayList ya se ha implementado. Cada vez que el espacio de almacenamiento no sea suficiente, expandirá automáticamente el espacio a 1,5 veces el tamaño

Sin embargo, debe prestar atención aquí, porque la operación de expansión implica la aplicación de memoria y el movimiento de datos, lo que lleva mucho tiempo. Por lo tanto, si el tamaño de los datos que se almacenarán se puede determinar de antemano, es mejor especificar el tamaño de los datos de antemano al crear ArrayList.

Por ejemplo, desea extraer 10 000 datos de la base de datos y colocarlos en ArrayList. Mire las siguientes líneas de código. Por el contrario, especificar el tamaño de los datos por adelantado puede ahorrar una gran cantidad de aplicaciones de memoria y operaciones de movimiento de datos.

ArrayList<User> users = new ArrayList(10000);
for (int i = 0; i < 10000; ++i) {
    
    
 users.add(xxx);
}

Entonces, ¿la matriz es inútil? Por supuesto que no, a veces es más apropiado usar una matriz

1. Java ArrayList no puede almacenar tipos básicos, como int y long, y debe empaquetarse como clases Integer y Long, mientras que Autoboxing y Unboxing consumirán una cierta cantidad de rendimiento, por lo que si presta especial atención al rendimiento o desea usar tipos básicos, puede usar matrices
2. Si el tamaño de los datos se conoce de antemano y la operación en los datos es muy simple, la mayoría de los métodos proporcionados por ArrayList no se usan y la matriz también se puede usar directamente.
3. Otra es que cuando se van a representar arreglos multidimensionales, a menudo es más intuitivo usar arreglos. Por ejemplo Object[][] array, si usa un contenedor, debe definirlo así:ArrayList<ArrayList> array

Para el desarrollo comercial, basta con utilizar el contenedor directamente, ahorrando tiempo y esfuerzo. Después de todo, una pérdida de rendimiento no afectará en absoluto al rendimiento general del sistema. Pero si está realizando un desarrollo de muy bajo nivel, como el desarrollo de un marco de red, la optimización del rendimiento debe ser extrema.En este momento, los arreglos serán mejores que los contenedores y se convertirán en la primera opción.

3.5 ¿Por qué las matrices comienzan a numerarse desde 0 en lugar de 1 en la mayoría de los lenguajes de programación?

Desde el modelo de memoria de almacenamiento en matriz, la definición más precisa de "subíndice" debería ser "compensación". Como se mencionó anteriormente, si a se usa para representar la primera dirección de la matriz, a[0] es la posición con un desplazamiento de 0, es decir, la primera dirección, y a[k] representa el desplazamiento de posición por k type_size, por lo que solo necesita usar esta fórmula para calcular la dirección de memoria de a[k]:

a[k]_dirección = base_dirección + k * tipo_tamaño

Sin embargo, si la matriz comienza a contar desde 1, entonces la dirección de memoria para calcular el elemento de la matriz a[k] se convierte en:

a[k]_dirección = base_dirección + (k - 1) * tipo_tamaño

Comparando las dos fórmulas, no es difícil encontrar que comenzando la numeración desde 1, cada acceso aleatorio a un elemento de la matriz requiere una operación de resta más.Para la CPU, es una instrucción de resta más.

Los arreglos son una estructura de datos muy básica, y el acceso aleatorio a los elementos del arreglo a través de subíndices es una operación de programación muy básica. La optimización de la eficiencia debe ser lo más extrema posible. Entonces, para reducir una operación de resta, la matriz elige comenzar a numerar desde 0 en lugar de 1

Sin embargo, no importa cuántas explicaciones se den arriba, no es una prueba abrumadora de que el número inicial de la matriz debe comenzar con 0. La razón más importante puede ser razones históricas

Los diseñadores del lenguaje C comenzaron a contar los subíndices de la matriz con 0, y luego los lenguajes de alto nivel como Java y JavaScript siguieron al lenguaje C, o en otras palabras, para reducir el costo de aprendizaje de los programadores del lenguaje C que aprenden Java hasta cierto punto, continuaron usando el hábito de contar desde 0. De hecho, las matrices no comienzan a contar desde 0 en muchos lenguajes, como Matlab. Incluso hay algunos lenguajes que admiten subíndices negativos, como Python

4. Lista vinculada

4.1 Estructura de lista enlazada

Una lista enlazada es una estructura de datos un poco más compleja que una matriz. Estas dos estructuras de datos muy básicas y de uso común a menudo se comparan juntas. Así que vamos a ver cuál es la diferencia entre los dos

estructura de almacenamiento subyacente

Como se muestra en la figura a continuación, la matriz necesita un espacio de memoria continuo para almacenar y los requisitos de memoria son relativamente altos. Si solicita una matriz con un tamaño de 100 MB, cuando no hay espacio de almacenamiento continuo y lo suficientemente grande en la memoria, incluso si el espacio total disponible restante de la memoria es superior a 100 MB, la aplicación seguirá fallando

Por el contrario, la lista enlazada no necesita un espacio de memoria continuo, sino que conecta un grupo de bloques de memoria dispersos en serie a través de "punteros", por lo que si solicitas una lista enlazada con un tamaño de 100 MB, no habrá ningún problema.

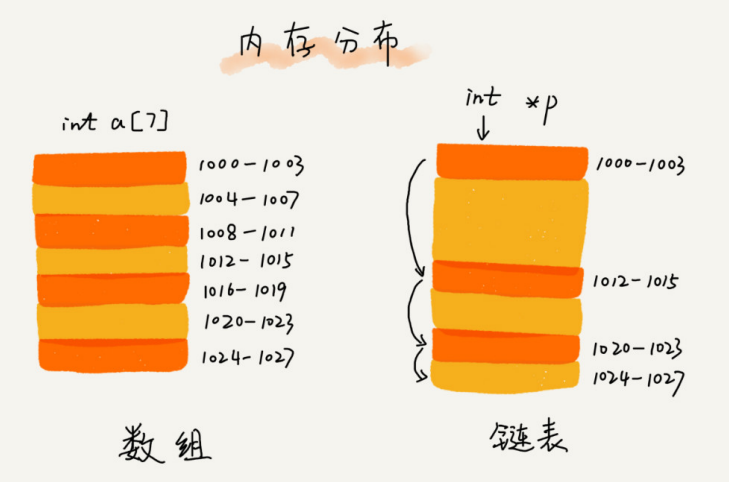
Hay varias estructuras de listas enlazadas. Estas son las tres estructuras de listas enlazadas más comunes. Son: lista enlazada simple, lista enlazada doble y lista enlazada circular.

1. Lista enlazada simple

Como se acaba de mencionar, la lista enlazada conecta un grupo de bloques de memoria dispersos a través de punteros. Entre ellos, el bloque de memoria se denomina "nodo" de la lista enlazada. Para unir todos los nodos, además de almacenar datos, cada nodo de la lista enlazada también necesita registrar la dirección del siguiente nodo en la cadena. Como se muestra en la figura, el puntero que registra la dirección del siguiente nodo se denomina puntero sucesor siguiente.

Como se puede ver en la figura anterior, hay dos nodos especiales, que son el primer nodo y el último nodo. Es costumbre llamar al primer nodo el nodo de cabeza y al último nodo el nodo de cola. Entre ellos, el nodo principal se usa para registrar la dirección base de la lista enlazada. Con él, puede recorrer para obtener toda la lista vinculada. La característica especial del nodo final es: el puntero no apunta al siguiente nodo, sino que apunta a una dirección vacía NULL, lo que indica que este es el
último nodo en la lista enlazada

Al igual que las matrices, las listas vinculadas también admiten operaciones de búsqueda, inserción y eliminación de datos.

Al realizar operaciones de inserción y eliminación de arreglos, para mantener la continuidad de los datos de la memoria, es necesario mover una gran cantidad de datos, por lo que la complejidad del tiempo es O ( n ) $O\left(n\right)$ . Al insertar o eliminar un dato en la lista enlazada, no hay necesidad de mover nodos para mantener la continuidad de la memoria, porque el espacio de almacenamiento de la lista enlazada en sí no es continuo. Por lo tanto, insertar y eliminar un dato en la lista enlazada es muy rápido.

Como se muestra en la figura a continuación, para las operaciones de inserción y eliminación de la lista enlazada, solo se deben considerar los cambios de puntero de los nodos adyacentes, por lo que la complejidad de tiempo correspondiente es O ( 1 ) O(1 $O\left(1\right)$

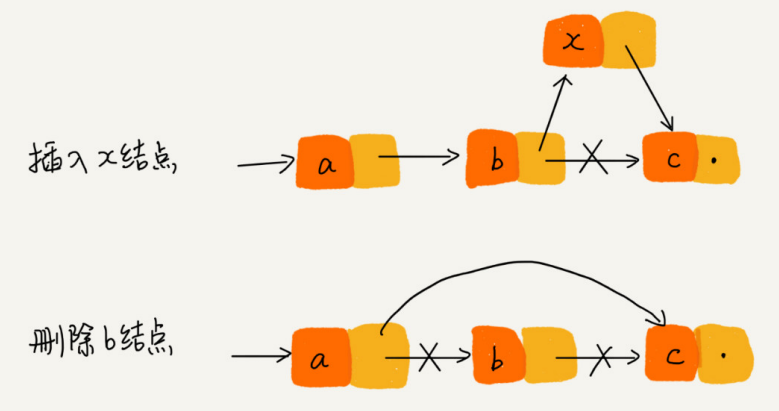
Sin embargo, hay pros y contras. Si una lista enlazada quiere acceder aleatoriamente al k-ésimo elemento, no es tan eficiente como una matriz. Debido a que los datos en la lista enlazada no se almacenan continuamente, es imposible calcular directamente la dirección de memoria correspondiente a través de la fórmula de direccionamiento de acuerdo con la primera dirección y el subíndice como una matriz, sino que debe atravesar un nodo por uno de acuerdo con el puntero hasta que se encuentre el nodo correspondiente.

Puedes pensar en una lista enlazada como un equipo. Todos en el equipo solo saben quién es la persona que está detrás de ellos, así que cuando quieras saber quién es la persona en el k-ésimo lugar, debes comenzar desde la primera persona y contar uno por uno. Por lo tanto, el rendimiento del acceso aleatorio de la lista enlazada no es tan bueno como el de la matriz, lo que requiere $O\left(n\right)$ tiempo complejidad

2. Lista enlazada circular

Una lista enlazada circular es un tipo especial de lista enlazada simple. De hecho, la lista enlazada circular también es muy simple. La única diferencia entre esta y la lista enlazada individualmente es el nodo de cola. El puntero del nodo final de la lista enlazada individualmente apunta a una dirección vacía, lo que indica que este es el último nodo. El puntero del nodo final de la lista enlazada circular apunta al nodo principal de la lista enlazada. Como se muestra en la figura a continuación, está conectado de extremo a extremo como un anillo, por lo que se denomina lista enlazada "circular".

En comparación con la lista enlazada simple, la ventaja de la lista enlazada circular es que es más conveniente ir desde el final de la cadena hasta el principio de la cadena. Cuando los datos a tratar tienen las características de una estructura en anillo, es especialmente adecuado utilizar una lista enlazada circular. Como el famoso problema de Joseph. Aunque también se puede implementar con una lista enlazada simple, si se implementa con una lista enlazada circular, el código será mucho más simple

3. Lista doblemente enlazada

La lista enlazada unidireccional tiene solo una dirección, y el nodo tiene solo un puntero sucesor que apunta al siguiente nodo. La lista doblemente enlazada, como sugiere el nombre, admite dos direcciones: cada nodo tiene más de un puntero sucesor que apunta al siguiente nodo y un puntero predecesor que apunta al nodo anterior.

La lista doblemente enlazada requiere dos espacios adicionales para almacenar la dirección del nodo sucesor y el nodo predecesor. Por lo tanto, si se almacena la misma cantidad de datos, la lista de enlaces dobles ocupa más espacio de memoria que la lista de enlaces simples. Aunque dos punteros son una pérdida de espacio de almacenamiento, pueden admitir el recorrido bidireccional, lo que también brinda la flexibilidad de las operaciones de listas doblemente vinculadas. En comparación con la lista enlazada simple, ¿qué tipo de problema es adecuada para resolver la lista doblemente enlazada?

Desde un punto de vista estructural, una lista doblemente enlazada puede soportar $En\; el\; caso\; de\; complejidad\; temporal\; O\left(1\right)$ , encuentre el nodo predecesor Es esta característica la que hace que las operaciones de inserción y eliminación de la lista doblemente enlazada en algunos casos sean más simples y eficientes que las de la lista enlazada simple.

En este momento, se puede decir que la complejidad temporal de las operaciones de inserción y eliminación de la lista enlazada simple mencionada anteriormente ya es $O\left(1\right)$ , ¿qué tan eficiente puede ser una lista doblemente enlazada? El análisis anterior es más teórico, y muchos libros de estructuras de datos y algoritmos dirán esto, pero esta declaración es en realidad inexacta o tiene requisitos previos. Analicemos las dos operaciones de la lista enlazada aquí.

Operación de eliminación : en el desarrollo de software real, eliminar una parte de los datos de la lista vinculada no es más que las siguientes dos situaciones

• Eliminar los nodos cuyo valor es igual a un valor dado entre los nodos
• Eliminar el nodo al que apunta el puntero dado

Para el primer caso, ya sea una lista de un solo enlace o una lista de enlaces dobles, para encontrar un nodo cuyo valor sea igual a un valor dado, es necesario recorrer y comparar uno a uno desde el nodo principal hasta encontrar un nodo cuyo valor sea igual a un valor dado, y luego eliminarlo mediante la operación de puntero mencionada anteriormente.

Aunque la complejidad del tiempo de la operación de borrado simple es $O\left(1\right)$ , pero el tiempo de búsqueda transversal es el principal punto que consume mucho tiempo, y la complejidad de tiempo correspondiente es$O\left(n\right)$ . De acuerdo con la regla de la suma en el análisis de complejidad temporal, la complejidad temporal total de la operación de lista enlazada correspondiente al nodo cuyo valor es igual al valor dado es$O\left(n\right)$

Para el segundo caso, se ha encontrado el nodo a eliminar, pero para eliminar un nodo q se necesita conocer su nodo predecesor, y la lista enlazada simple no admite obtener directamente el nodo predecesor, por lo que para encontrar el nodo predecesor, aún es necesario recorrer la lista enlazada desde el nodo principal hasta, indicando que p es el nodo predecesor de p->next=qq

Pero para listas doblemente enlazadas, esta situación es más ventajosa. Debido a que los nodos en la lista doblemente enlazada ya han guardado los punteros de los nodos predecesores, no hay necesidad de atravesar como una lista enlazada simple. Por lo tanto, para el segundo caso, O(n)la complejidad de tiempo requerida para la operación de borrado de la lista con enlace simple es , mientras que la lista con enlace doble solo necesita realizarse O(1)dentro de la complejidad de tiempo de !

La operación de inserción es la misma, si desea insertar un nodo delante de un nodo específico en la lista enlazada, la lista doblemente enlazada tiene una gran ventaja sobre la lista enlazada simple. Una lista doblemente enlazada se puede hacer en $O\left(1\right)$ la complejidad del tiempo está hecha, mientras que la lista enlazada unidireccional necesita$O\left(n\right)$ tiempo complejidad

Además de las ventajas de las operaciones de inserción y eliminación, para una lista enlazada ordenada, la eficiencia de la consulta valor por valor de una lista doblemente enlazada también es mayor que la de una lista enlazada simple. Debido a que se puede registrar la posición p de la última búsqueda, y cada vez que se realiza una consulta, se decide si buscar hacia adelante o hacia atrás según la relación entre el valor a buscar y el tamaño de p, por lo que en promedio solo se necesita buscar la mitad de los datos

¿Crees que las listas con enlaces dobles son más eficientes que las listas con enlaces simples? Esta es la razón por la que en el desarrollo de software real, aunque la lista doblemente enlazada consume más memoria, todavía se usa más ampliamente que la lista enlazada simple. Si está familiarizado con el lenguaje Java, debe haber utilizado el contenedor LinkedHashMap. Si profundiza en el principio de implementación de LinkedHashMap, encontrará que se utiliza la estructura de datos de la lista doblemente enlazada.

De hecho, hay un punto de conocimiento más importante que debes dominar, es decir, la idea de diseño de intercambiar espacio por tiempo . Cuando el espacio de memoria es suficiente, si persigue más la velocidad de ejecución del código, puede elegir un algoritmo o estructura de datos con una complejidad de espacio relativamente alta pero una complejidad de tiempo relativamente baja. Por el contrario, si la memoria es relativamente escasa, como el código que se ejecuta en un teléfono móvil o una microcomputadora de un solo chip, en este momento es necesario revertir la idea de diseño de intercambiar tiempo por espacio.

El almacenamiento en caché es en realidad la idea de diseño de usar el espacio por tiempo. Si los datos se almacenan en el disco duro, ahorrará memoria, pero cada vez que se buscan los datos, se debe consultar el disco duro, que será más lento. Sin embargo, si los datos se cargan en la memoria de antemano a través de la tecnología de almacenamiento en caché, aunque consumirá más espacio de memoria, la velocidad de cada consulta de datos mejorará considerablemente.

Para los programas que se ejecutan lentamente, pueden optimizarse consumiendo más memoria (espacio por tiempo); para los programas que consumen demasiada memoria, pueden reducir el consumo de memoria consumiendo más tiempo (tiempo por espacio)

Después de entender la lista enlazada circular y la lista doblemente enlazada, si estas dos listas enlazadas se integran juntas, será una nueva versión: lista doblemente enlazada

4.2 Comparación de rendimiento de lista enlazada VS matriz

Las matrices y las listas enlazadas son dos formas muy diferentes de organizar la memoria. Es precisamente debido a la diferencia en el almacenamiento de memoria que la complejidad temporal de sus operaciones de inserción, eliminación y acceso aleatorio es todo lo contrario.

Sin embargo, la comparación entre arreglos y listas enlazadas no puede limitarse a la complejidad del tiempo. Además, en el desarrollo de software real, no es posible decidir qué estructura de datos usar para almacenar datos solo mediante análisis de complejidad.

La matriz es simple y fácil de usar. La implementación utiliza un espacio de memoria continuo. Los datos en la matriz se pueden leer de antemano con la ayuda del mecanismo de caché de la CPU, por lo que la eficiencia de acceso es mayor. La lista enlazada no se almacena continuamente en la memoria, por lo que no es compatible con la memoria caché de la CPU y no hay forma de leer con anticipación de manera efectiva.

La desventaja de una matriz es que su tamaño es fijo y, una vez que se declara, ocupará todo el espacio de memoria continua. Si la matriz declarada es demasiado grande, es posible que el sistema no tenga suficiente espacio de memoria contiguo asignado, lo que resultará en "memoria insuficiente". Si la matriz declarada es demasiado pequeña, puede que no sea suficiente. En este momento, solo podemos solicitar un espacio de memoria más grande y copiar la matriz original en él, lo que lleva mucho tiempo. La lista vinculada en sí no tiene límite de tamaño y, naturalmente, admite la expansión dinámica, que es la mayor diferencia entre ella y la matriz.

Java 中的 ArrayList 容器虽然支持动态扩容，但实际上还是数组的拷贝操作。当往支持动态扩容的数组中插入一个数据时，如果数组中没有空闲空间了，就会申请一个更大的空间，将数据拷贝过去，而数据拷贝的操作是非常耗时的

举一个稍微极端的例子。如果用 ArrayList 存储了了 1GB 大小的数据，这个时候已经没有空闲空间了，当再插入数据的时候，ArrayList 会申请一个 1.5GB 大小的存储空间，并且把原来那 1GB 的数据拷贝到新申请的空间上。听起来是不是就很耗时？

除此之外，如果代码对内存的使用非常苛刻，那数组就更适合。因为链表中的每个结点都需要消耗额外的存储空间去存储一份指向下一个结点的指针，所以内存消耗会翻倍。而且，对链表进行频繁的插入、删除操作，还会导致频繁的内存申请和释放，容易造成内存碎片，如果是 Java 语言，就有可能会导致频繁的 GC（Garbage Collection，垃圾回收）。所以，在实际的开发中，针对不同类型的项目，要根据具体情况，权衡究竟是选择数组还是链表

4.3 如何基于链表实现 LRU 缓存淘汰算法？

缓存是一种提高数据读取性能的技术，在硬件设计、软件开发中都有着非常广泛的应用，比如常见的 CPU 缓存、数据库缓存、浏览器缓存等等

缓存的大小有限，当缓存被用满时，哪些数据应该被清理出去，哪些数据应该被保留？这就需要缓存淘汰策略来决定。常见的策略有三种：先进先出策略 FIFO（First In，First Out）、最少使用策略 LFU（Least Frequently Used）、最近最少使用策略 LRU（Least Recently Used）

这些策略其实见名知义，那么如何基于链表实现 LRU 缓存淘汰算法呢？

可以维护一个有序单链表，越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时，从链表头开始顺序遍历链表

1. 如果此数据之前已经被缓存在链表中了，遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部

2. Si los datos no están en la lista enlazada de caché, se pueden dividir en dos situaciones:

   • Si el caché no está lleno en este momento, inserte este nodo directamente en el encabezado de la lista enlazada
   • Si la memoria caché está llena en este momento, se elimina el nodo final de la lista vinculada y se inserta un nuevo nodo de datos en el encabezado de la lista vinculada.

De esta forma se implementa una caché LRU con una lista enlazada, ¿es muy sencillo?

Ahora veamos la complejidad temporal del acceso a la memoria caché m. Debido a que la lista vinculada debe recorrerse independientemente de si la memoria caché está llena o no, la complejidad temporal del acceso a la memoria caché es $O\left(n\right)$

De hecho, puede continuar optimizando esta idea de implementación, como la introducción de una tabla hash (tabla Hash) para registrar la ubicación de cada dato, reduciendo la complejidad del tiempo de acceso a la memoria caché a O ( 1 ) $O\left(1\right)$

Además de la idea de implementación basada en la lista enlazada, de hecho, las matrices también se pueden usar para implementar la estrategia de eliminación de caché LRU.

4.4 ¿Cómo escribir fácilmente el código correcto de la lista enlazada?

No es fácil escribir bien el código de una lista vinculada, especialmente aquellas operaciones complicadas de listas vinculadas, como la inversión de listas vinculadas, la fusión de listas vinculadas ordenadas, etc., son muy propensas a errores al escribir. ¿Por qué el código de lista enlazada es tan difícil de escribir? ¿Cómo podemos escribir el código correcto de la lista enlazada más fácilmente?

1. Comprender el significado de punteros o referencias

De hecho, no es difícil entender la estructura de la lista enlazada, pero una vez que se mezcla con punteros, es fácil confundirse. Por lo tanto, si desea escribir el código de la lista enlazada correctamente, primero debe comprender el puntero

Algunos lenguajes tienen el concepto de "punteros", como el lenguaje C; algunos lenguajes no tienen punteros, sino que usan "referencias", como Java y Python. Independientemente de si se trata de un "puntero" o una "referencia", de hecho, sus significados son los mismos y todas son direcciones de memoria que almacenan el objeto apuntado.

De hecho, para la comprensión de los punteros, solo necesita recordar la siguiente oración:

Asignar una variable a un puntero es en realidad asignar la dirección de la variable al puntero o, por el contrario, la dirección de memoria de la variable se almacena en el puntero, apuntando a la variable, y la variable se puede encontrar a través del puntero.

Al escribir código de lista enlazada, a menudo hay tales códigos: · p->next = q. Esta línea de código significa que el siguiente puntero en el nodo p almacena la dirección de memoria del nodo q

También hay uno más complicado, que se usa a menudo cuando se escribe código de lista enlazada: p->next = p->next->next. Esta línea de código indica que el siguiente puntero del nodo p almacena la dirección de memoria del siguiente nodo del nodo p

Una vez que haya dominado el concepto de punteros o referencias, debería poder comprender fácilmente el código de la lista vinculada.

2. Tenga cuidado con los punteros perdidos y las fugas de memoria

Al escribir el código de la lista vinculada, el puntero apunta de un lado a otro, y no sé a dónde apunta por un tiempo. Por lo tanto, al escribir, tenga cuidado de no perder el puntero.

¿Cómo se pierden a menudo los punteros? Aquí hay un ejemplo de la operación de inserción de una lista enlazada individualmente

Como se muestra en la figura, se espera insertar el nodo x entre el nodo ay el nodo adyacente b, asumiendo que el puntero actual p apunta al nodo a. Si la implementación del código se cambia a la siguiente, se producirán pérdidas de puntero y pérdida de memoria

p->next = x; // 将 p 的 next 指针指向 x 结点；
x->next = p->next; // 将 x 的结点的 next 指针指向 b 结点；

Después del primer paso, el puntero p->siguiente ya no apunta al nodo b, sino que apunta al nodo x. La segunda línea de código es equivalente a asignar x a x->next, apuntándose a sí mismo. Por lo tanto, toda la lista enlazada se divide en dos mitades y no se puede acceder a todos los nodos desde el nodo b en adelante.

Para algunos lenguajes, como el lenguaje C, la gestión de la memoria es responsabilidad del programador, si no se libera manualmente el espacio de memoria correspondiente al nodo, se producirán pérdidas de memoria. Por lo tanto, al insertar un nodo, debe prestar atención al orden de las operaciones. Primero debe apuntar el siguiente puntero del nodo x al nodo b, y luego apuntar el siguiente puntero del nodo a al nodo x, para que el puntero no se pierda, lo que provocaría pérdidas de memoria. Entonces, para el código insertado hace un momento, solo necesita invertir el orden del código en la línea 1 y la línea 2

De manera similar, al eliminar un nodo de lista vinculada, también debe recordar liberar manualmente el espacio de memoria; de lo contrario, también se producirán pérdidas de memoria. Por supuesto, para un lenguaje de programación como Java, donde la máquina virtual administra automáticamente la memoria, no hay necesidad de considerar tanto

3. Use Sentinel para simplificar la dificultad de implementación

Primero, revisemos las operaciones de inserción y eliminación de la lista enlazada individualmente. Si inserta un nuevo nodo después del nodo p, solo necesita las siguientes dos líneas de código para hacerlo

new_node->next = p->next;
p->next = new_node;

Sin embargo, al insertar el primer nodo en una lista enlazada vacía, la lógica de ahora no se puede utilizar. Se requiere el siguiente procesamiento especial, donde head representa el nodo principal de la lista enlazada. Por lo tanto, a partir de este código, se puede encontrar que para la operación de inserción de la lista enlazada simple, la lógica de inserción del primer nodo y otros nodos es diferente

if (head == null) {
    
    
   head = new_node;
}

Veamos la operación de eliminación del nodo de lista enlazada individualmente. Si desea eliminar el nodo sucesor del nodo p, solo necesita una línea de código para hacerlo

p->next = p->next->next;

Sin embargo, si desea eliminar el último nodo de la lista vinculada, el código de eliminación anterior no funcionará. Similar a la inserción, también se requiere un manejo especial para este caso.

if (head->next == null) {
    
    
   head = null;
}

Del anterior análisis paso a paso, se puede observar que para las operaciones de inserción y eliminación de la lista enlazada se necesita realizar un manejo especial para el caso de insertar el primer nodo y eliminar el último nodo. De esta manera, el código será engorroso de implementar, no conciso, y es fácil cometer errores debido a una consideración incompleta. ¿Cómo resolver este problema?

Sentinel , el centinela mencionado aquí es para resolver el "problema de límites" y no participa directamente en la lógica empresarial

head = nullIndica que no hay más nodos en la lista enlazada. Donde head representa el puntero del nodo principal, apuntando al primer nodo en la lista enlazada. Si se introduce un ganglio centinela, en cualquier momento, independientemente de si la lista enlazada está vacía o no, el puntero de la cabeza siempre apuntará a este ganglio centinela. Este tipo de lista enlazada con ganglios centinela también se denomina lista enlazada principal. Por el contrario, una lista enlazada sin un ganglio centinela se denomina lista enlazada sin cabeza.

Como se muestra en la figura a continuación, se puede encontrar que el nodo centinela no almacena datos. Debido a que el nodo centinela siempre ha existido, la inserción del primer nodo y la inserción de otros nodos, la eliminación del último nodo y la eliminación de otros nodos se pueden unificar en el mismo código para implementar la lógica.

De hecho, esta técnica de usar centinelas para simplificar la dificultad de programación se usa en muchas implementaciones de código, como clasificación por inserción, clasificación por fusión, programación dinámica, etc.

4. Preste atención al procesamiento de las condiciones de contorno

En el desarrollo de software, el código es más propenso a errores en algunas situaciones límite o anormales. El código de lista enlazada no es una excepción. Para implementar el código de lista enlazada sin errores, es necesario comprobar si las condiciones de contorno se tienen en cuenta durante el proceso de escritura y después de que se complete la escritura, y si el código puede ejecutarse correctamente bajo las condiciones de contorno.

Hay varias condiciones de contorno que se utilizan a menudo para comprobar si el código de la lista enlazada es correcto:

• ¿Funciona correctamente el código si la lista enlazada está vacía?
• ¿Funciona correctamente el código si la lista enlazada contiene solo un nodo?
• ¿Funciona correctamente el código si la lista enlazada contiene solo dos nodos?
• ¿Funciona correctamente la lógica del código cuando se trata de nodos de cabeza y nodos de cola?

Después de escribir el código de la lista enlazada, además de verificar si el código puede funcionar en condiciones normales, también depende de si el código aún puede funcionar correctamente en las condiciones límite anteriores. Si no hay problemas bajo estas condiciones de contorno, básicamente se puede considerar que no hay problema.

Por supuesto, las condiciones de contorno no se limitan a las enumeradas anteriormente. Para diferentes escenarios, puede haber condiciones límite específicas. Esto debe ser pensado por usted mismo, pero la rutina es la misma.

De hecho, no solo escriba código de lista enlazada, sino que al escribir cualquier código, no solo implemente las funciones en condiciones comerciales normales, sino que debe pensar más en las condiciones límite o las condiciones anormales que pueden encontrarse cuando se ejecuta el código. ¡Cómo lidiar con el encuentro, para que el código escrito sea lo suficientemente robusto!

5. Dibujar ejemplos para ayudar a pensar

Para las operaciones de lista enlazada un poco complicadas, como la inversión de lista enlazada única mencionada anteriormente, el puntero apunta aquí y allá durante un rato, y luego se marea durante un rato. Siempre siento que mi capacidad cerebral no es suficiente y no puedo pensar con claridad. Entonces, en este momento, se pueden usar otros métodos para ayudar a la comprensión, como: método de ejemplo y método de dibujo

Puedes encontrar un ejemplo específico, dibujarlo en un papel, liberar algo de capacidad cerebral y dejar más para el pensamiento lógico, de modo que sientas que tu pensamiento es mucho más claro. Por ejemplo, una operación como la inserción de un dato en una lista enlazada individualmente generalmente toma un ejemplo de varias situaciones y dibuja los cambios de la lista enlazada antes y después de la inserción, como se muestra en la figura.

Es mucho más fácil escribir código mirando la imagen. Además, después de escribir el código, también puede dar algunos ejemplos, dibujar en papel, seguir el código y encontrar fácilmente errores en el código.

6. Escribe más y practica más, no hay atajos

¡La práctica hace la perfección! Aquí hay 5 operaciones comunes de listas enlazadas. Siempre que pueda escribir estas operaciones de manera competente, escríbalas varias veces si no está familiarizado con ellas, para que nunca tenga miedo de escribir códigos de listas enlazadas nuevamente.

• Lista inversa de enlaces simples
• Detección de anillos en lista enlazada
• Fusión de dos listas enlazadas ordenadas
• Eliminar el último nodo n de la lista enlazada
• Encuentra el nodo medio de la lista enlazada

5. Apilar

5.1 ¿Cómo entender "pila"?

Un ejemplo muy adecuado de una "pila" es una pila de platos apilados uno encima del otro. Cuando solemos colocar los platos, los colocamos uno a uno de abajo hacia arriba; cuando los sacamos, también los tomamos uno a uno de arriba a abajo, y no podemos sacarlos del medio arbitrariamente. Último en entrar, primero en salir, último en salir avanzado , esta es una estructura típica de "pila"

Por las características operativas de la pila, la pila es una tabla lineal con "operaciones restringidas" , que solo permite insertar y borrar datos en un extremo.

De hecho, desde un punto de vista funcional, una matriz o una lista enlazada puede reemplazar una pila, pero una estructura de datos específica es una abstracción de una escena específica. Además, una matriz o una lista enlazada expone demasiadas interfaces de operación. La operación es de hecho flexible y gratuita, pero es relativamente incontrolable cuando se usa y, naturalmente, es más propensa a errores.

Cuando un conjunto de datos solo implica la inserción y eliminación de datos en un extremo y satisface las características de último en entrar, primero en salir y primero en entrar, último en salir, se debe preferir la estructura de datos de "pila".

5.2 ¿Cómo implementar un "stack"?

La pila incluye principalmente dos operaciones, empujar y sacar, es decir, insertar datos en la parte superior de la pila y eliminar datos de la parte superior de la pila.

De hecho, una pila se puede implementar con una matriz o una lista enlazada. Una pila implementada con una matriz se llama pila secuencial, y una pila implementada con una lista enlazada se llama pila enlazada.

Aquí se implementa una pila secuencial basada en matriz

// 基于数组实现的顺序栈
public class ArrayStack {
    
    
    private String[] items; // 数组
    private int count; // 栈中元素个数
    private int n; // 栈的大小
    // 初始化数组，申请一个大小为 n 的数组空间
    public ArrayStack(int n) {
    
    
        this.items = new String[n];
        this.n = n;
        this.count = 0;
    }
    // 入栈操作
    public boolean push(String item) {
    
    
        // 数组空间不够了，直接返回 false，入栈失败。
        if (count == n) return false;
        // 将 item 放到下标为 count 的位置，并且 count 加一
        items[count] = item;
        ++count;
        return true;
    }

    // 出栈操作
    public String pop() {
    
    
        // 栈为空，则直接返回 null
        if (count == 0) return null;
        // 返回下标为 count-1 的数组元素，并且栈中元素个数 count 减一
        String tmp = items[count - 1];
        --count;
        return tmp;
    }
}

Después de comprender la definición y las operaciones básicas, ¿cuál es la complejidad temporal y espacial de sus operaciones?

Independientemente de si se trata de una pila secuencial o una pila encadenada, solo una matriz con un tamaño de n es suficiente para almacenar datos. En el proceso de empujar y abrir, solo se necesitan uno o dos espacios de almacenamiento variables temporales, por lo que la complejidad del espacio es $O\left(1\right)$

Tenga en cuenta que almacenar datos aquí requiere una matriz de tamaño n, por no decir que la complejidad del espacio es $O\left(n\right)$ . Porque estos n espacios son necesarios y no se pueden omitir. Entonces, cuando hablamos de la complejidad del espacio, significa que además del espacio de almacenamiento de datos original, la operación del algoritmo también requiere espacio de almacenamiento adicional.

Independientemente de si se trata de una pila secuencial o una pila en cadena, empujar y sacar solo implica la operación de datos individuales en la parte superior de la pila, por lo que la complejidad del tiempo es O ( 1 ) $O\left(1\right)$

5.3 Pila secuencial compatible con la expansión dinámica

刚才那个基于数组实现的栈，是一个固定大小的栈，也就是说，在初始化栈时需要事先指定栈的大小。当栈满之后，就无法再往栈里添加数据了。尽管链式栈的大小不受限，但要存储 next 指针，内存消耗相对较多。那如何基于数组实现一个可以支持动态扩容的栈呢？

在数组那一节，实现一个支持动态扩容的数组的方法是当数组空间不够时，就重新申请一块更大的内存，将原来数组中数据统统拷贝过去，这样就实现了一个支持动态扩容的数组

所以，如果要实现一个支持动态扩容的栈，只需要底层依赖一个支持动态扩容的数组就可以了。当栈满了之后，就申请一个更大的数组，将原来的数据搬移到新数组中，如下图

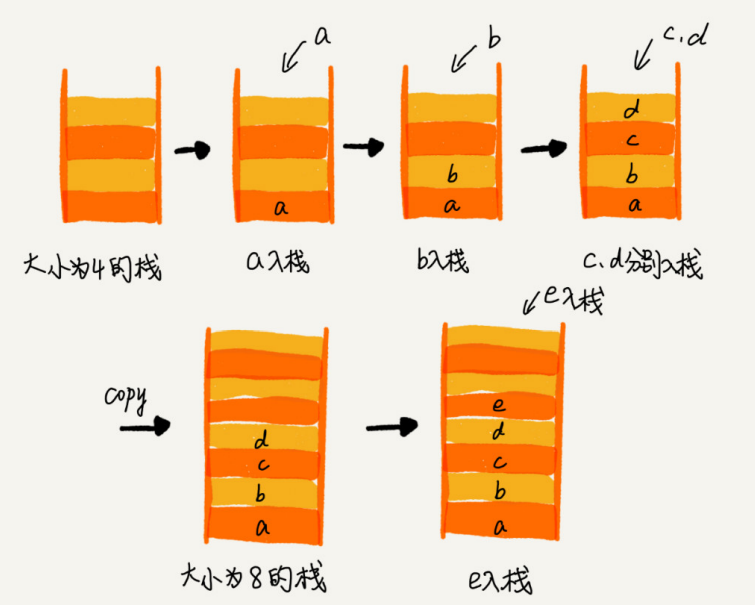
实际上，支持动态扩容的顺序栈，平时开发中并不常用到。主要还是复杂度分析

对于出栈操作来说，不会涉及内存的重新申请和数据的搬移，所以出栈的时间复杂度仍然是 $O(1)$。但是，对于入栈操作来说，情况就不一样了。当栈中有空闲空间时，入栈操作的时间复杂度为 $O(1)$。但当空间不够时，就需要重新申请内存和数据搬移，所以时间复杂度就变成了 $O(n)$

也就是说，对于入栈操作来说，最好情况时间复杂度是 $O(1)$，最坏情况时间复杂度是 $O\left(n\right)$ . ¿Cuál es la complejidad del tiempo promedio? La complejidad de tiempo promedio de esta operación de empuje se puede analizar mediante un análisis amortizado

Para facilitar el análisis, es necesario hacer algunas suposiciones y definiciones por adelantado:

• Cuando el espacio de la pila no sea suficiente, vuelva a solicitar una matriz del doble del tamaño original
• Para simplificar el análisis, se supone que solo hay operaciones push y no pop.
• Defina la operación de inserción que no implica la transferencia de memoria como una operación de inserción simple, y la complejidad del tiempo es $O\left(1\right)$

Si el tamaño de la pila actual es K y está lleno, cuando hay nuevos datos para insertar en la pila, es necesario volver a solicitar el doble del tamaño de la memoria, realizar K operaciones de movimiento de datos y luego insertarlos en la pila. Sin embargo, las siguientes operaciones de inserción de K-1 no necesitan volver a solicitar memoria y mover datos, por lo que estas operaciones de inserción de K-1 se pueden completar con una sola operación de inserción simple, como se muestra en la figura a continuación.

Estas K operaciones de inserción implican un total de K transferencias de datos y K operaciones de inserción simple. Si K transferencias de datos se amortizan en K operaciones de inserción, cada operación de inserción solo requiere una transferencia de datos y una operación de inserción simple. Por analogía, la complejidad temporal amortizada de la operación de pila es $O\left(1\right)$

Mediante el análisis real de este ejemplo, también se confirma lo mencionado anteriormente de que la complejidad del tiempo amortizado es generalmente igual a la complejidad del tiempo en el mejor de los casos. Porque en la mayoría de los casos, la complejidad temporal O de la operación de pila es $O\left(1\right)$ , degenera a O ( n ) O(n)solo en momentos individuales$O\left(n\right)$ , por lo que la operación de pila que consume mucho tiempo se asigna a otras operaciones de pila, y el tiempo promedio que consume está cerca de$O\left(1\right)$

5.4 Aplicación de la pila

5.4.1 Aplicación de pila en llamada de función

Como estructura de datos relativamente básica, la pila tiene muchos escenarios de aplicación. Entre ellos, uno de los escenarios de aplicación más clásicos es la pila de llamadas a funciones.

El sistema operativo asigna un espacio de memoria independiente para cada subproceso, y esta memoria se organiza en una estructura de "pila", que se utiliza para almacenar variables temporales cuando se llama a la función. Cada vez que se ingresa una función, la variable temporal se insertará en la pila como un marco de pila. Cuando la función llamada se ejecute y se devuelva, el marco de pila correspondiente a la función se extraerá de la pila. Por ejemplo

int main() {
    
    
    int a = 1;
    int ret = 0;
    int res = 0;
    ret = add(3, 5);
    res = a + ret;
    printf("%d", res);
    reuturn 0;
}
int add(int x, int y) {
    
    
    int sum = 0;
    sum = x + y;
    return sum;
}

Se puede ver en el código que main()la función llama add()a la función, obtiene el resultado del cálculo, lo agrega a la variable temporal a y finalmente imprime el valor de res. add()El diagrama de flujo es el siguiente, y la figura muestra el estado de la pila de llamadas de función cuando se ejecuta la función

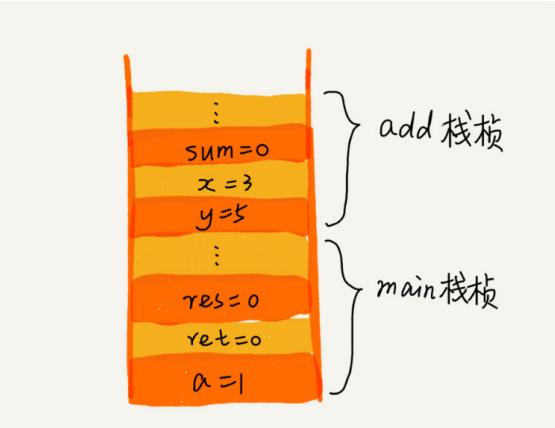
5.4.2 Aplicación de la pila en la evaluación de expresiones

Veamos otro escenario de aplicación común de la pila, cómo el compilador usa la pila para implementar la evaluación de expresiones.

Para facilitar la explicación, la expresión aritmética se simplifica para incluir solo las cuatro operaciones aritméticas de suma, resta, multiplicación y división, por ejemplo: $34+13\ast 9+44-12/3$ . Para estas cuatro operaciones aritméticas, el cerebro humano puede resolver rápidamente la respuesta, pero para una computadora es muy difícil entender la expresión en sí. ¿Cómo implementar tal función de evaluación de expresiones?

De hecho, el compilador se implementa a través de dos pilas. Uno contiene la pila de operandos y el otro contiene la pila de operadores. Atravesando expresiones de izquierda a derecha, cuando se encuentra un número, se inserta directamente en la pila de operandos; cuando se encuentra un operador, se compara con el elemento superior de la pila de operadores.

Si es mayor que la prioridad del elemento superior de la pila de operadores, inserte el operador actual en la pila; si es menor o igual que la prioridad del elemento superior de la pila de operadores, tome el operador superior de la pila de operadores, tome 2 operandos de la parte superior de la pila de operandos y luego realice cálculos, luego inserte los resultados calculados en la pila de operandos y continúe comparando

$3+5\ast 8-6$ El proceso de cálculo de esta expresión es el siguiente:

5.4.3 Aplicación de la pila en coincidencia de paréntesis

Puede usar la pila para verificar si los paréntesis en la expresión coinciden

Simplifica el fondo. Suponga que la expresión contiene solo tres tipos de corchetes, paréntesis (), corchetes [] y corchetes {}, y se pueden anidar arbitrariamente. Por ejemplo, {[{}]} o [{()}([])] son ​​formatos legales, pero {[}()] o [({)] son ​​formatos ilegales. Ahora que hay una cadena de expresión que contiene tres tipos de corchetes, ¿cómo verificar si es legal?

Las pilas también se pueden usar aquí. Use una pila para almacenar paréntesis izquierdos no coincidentes y escanee la cadena de izquierda a derecha. Cuando se escanea un paréntesis izquierdo, se coloca en la pila; cuando se escanea un paréntesis derecho, se toma un paréntesis izquierdo de la parte superior de la pila. Si puede coincidir, por ejemplo, con "(" coincide con ")", "[" coincide con "]", "{" coincide con "}", continúe escaneando las cadenas restantes. Si durante el proceso de escaneo, se encuentra un paréntesis derecho no coincidente o no hay datos en la pila, significa que el formato es ilegal.

Después de escanear todos los corchetes, si la pila está vacía, significa que la cadena está en un formato legal; de lo contrario, significa que hay un corchete izquierdo no coincidente, que es un formato ilegal

5.5 ¿Cómo implementar las funciones de avance y retroceso del navegador?

Después de visitar una serie de páginas abc, haga clic en el botón Atrás del navegador para ver las páginas b y a exploradas anteriormente. Cuando regresa a la página a y hace clic en el botón de avance, puede ver las páginas b y c nuevamente. Sin embargo, si regresa a la página b y hace clic en una nueva página d, ya no podrá ver la página c a través de las funciones de avance y retroceso.

¿Cómo? De hecho, usar dos pilas puede resolver perfectamente este problema.

Use dos pilas, X e Y, para empujar las páginas exploradas por primera vez en la pila X una por una. Cuando se hace clic en el botón Atrás, se extraerán de la pila X a su vez, y los datos extraídos se colocarán en la pila Y a su vez. Cuando se hace clic en el botón de avance, los datos se extraen secuencialmente de la pila Y y se colocan en la pila X. Cuando no hay datos en la pila X, significa que no hay una página para volver a navegar. Cuando no hay datos en la pila Y, significa que no hay una página para navegar haciendo clic en el botón de avance

Por ejemplo, después de ver las tres páginas a, b y c en secuencia, presione a, b y c en la pila por turno. En este momento, los datos de las dos pilas se ven así:

Después de volver de la página c a la página a mediante el botón Atrás del navegador, extraiga c y b de la pila X por turnos y colóquelos en la pila Y por turnos. En este momento, los datos de las dos pilas se ven así:

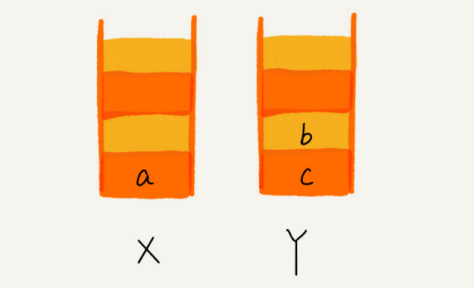
En este momento, quiero volver a ver la página b, así que hago clic en el botón de avance para volver a la página b, y luego extraigo b de la pila Y y la coloco en la pila X. En este momento, los datos de las dos pilas se ven así:

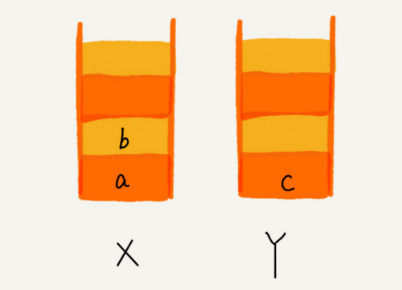
En este momento, la página b salta a una nueva página d, y la página c ya no se puede ver repetidamente a través de los botones de avance y retroceso, por lo que la pila Y debe borrarse. En este momento, los datos de las dos pilas se ven así:

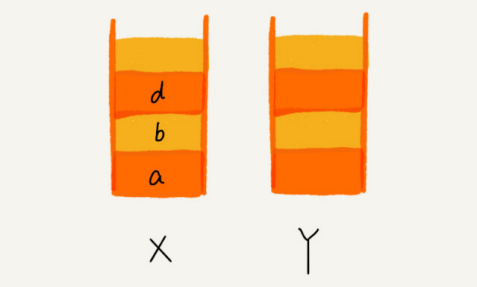
6. Cola

6.1 ¿Cómo entender "cola"?

El concepto de cola es muy fácil de entender. Se puede pensar en hacer cola para comprar boletos, primero en llegar, primero en comprar, y aquellos que llegan después solo pueden pararse al final y no se les permite saltar en la fila. Primero en entrar, primero en salir, esta es una "cola" típica

La pila solo admite dos operaciones básicas: empujar push()y sacar pop(). La cola es muy similar a la pila, y las operaciones admitidas también son muy limitadas. Las operaciones más básicas son dos: enqueue enqueue(), poner un dato al final de la cola; dequeue dequeue(), tomar un elemento de la cabeza de la cola.

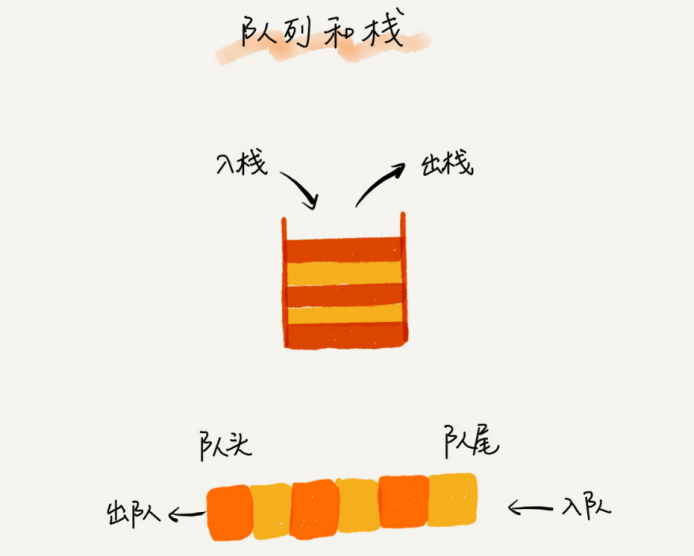
Por lo tanto, la cola, como la pila, también es una estructura de datos de tabla lineal con operaciones limitadas.

El concepto de cola es fácil de entender y las operaciones básicas son fáciles de dominar. Como una estructura de datos muy básica, las colas también se usan ampliamente, especialmente algunas colas con algunas características adicionales, como colas circulares, colas de bloqueo y colas concurrentes. Desempeñan un papel clave en el desarrollo de muchos sistemas, marcos y middleware de bajo nivel. Por ejemplo, el disruptor de colas de alto rendimiento y la memoria caché en anillo de Linux utilizan colas concurrentes circulares; la entrega de contratos concurrentes de Java utiliza ArrayBlockingQueue para implementar bloqueos justos, etc.

6.2 Colas secuenciales y colas encadenadas

Al igual que una pila, una cola también es una estructura de datos abstracta. Tiene la función de primero en entrar, primero en salir, y admite la inserción de elementos al final de la cola y la eliminación de elementos al principio de la cola Entonces, ¿cómo implementar una cola?

Al igual que las pilas, las colas se pueden implementar mediante matrices o listas vinculadas. Una pila implementada con una matriz se llama pila secuencial, y una pila implementada con una lista enlazada se llama pila enlazada. De manera similar, una cola implementada con una matriz se denomina cola secuencial, y una cola implementada con una lista vinculada se denomina cola encadenada.

Echemos un vistazo al método de implementación basado en la matriz.

// 用数组实现的队列
public class ArrayQueue {
    
    
    // 数组：items，数组大小：n
    private String[] items;
    private int n = 0;
    // head 表示队头下标，tail 表示队尾下标
    private int head = 0;
    private int tail = 0;
    // 申请一个大小为 capacity 的数组
    public ArrayQueue(int capacity) {
    
    
        items = new String[capacity];
        n = capacity;
    }
    // 入队
    public boolean enqueue(String item) {
    
    
        // 如果 tail == n 表示队列已经满了
        if (tail == n) return false;
        items[tail] = item;
        ++tail;
        return true;
    }
    // 出队
    public String dequeue() {
    
    
        // 如果 head == tail 表示队列为空
        if (head == tail) return null;
        String ret = items[head];
        ++head;
        return ret;
    }
}

Para la pila, solo se necesita un puntero a la parte superior de la pila. Pero la cola necesita dos punteros: uno es el puntero de cabeza, que apunta a la cabeza de la cola; el otro es el puntero de cola, que apunta a la cola de la cola.

Se puede entender combinando la siguiente figura. Cuando a, b, c y d se ponen en cola por turnos, el puntero de la cabeza en la cola apunta a la posición con el subíndice 0, y el puntero de la cola apunta a la posición con el subíndice 4

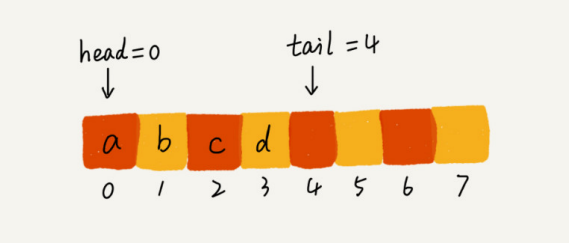
Después de llamar dos veces a la operación de eliminación de cola, el puntero de la cabeza en la cola apunta a la posición con el subíndice 2, y el puntero de la cola aún apunta a la posición con el subíndice 4.

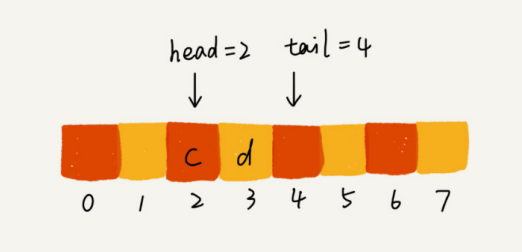
En este momento, debe haber sido descubierto.Con las operaciones continuas de entrada y salida, la cabeza y la cola continuarán moviéndose hacia atrás. Cuando la cola se mueve hacia el extremo derecho, incluso si todavía hay espacio libre en la matriz, es imposible continuar agregando datos a la cola. ¿Cómo resolver este problema?

En la sección anterior sobre matrices, también encontré un problema similar, es decir, la operación de eliminación de la matriz hará que los datos de la matriz sean discontinuos. ¡El método utilizado en ese momento fue el movimiento de datos! Sin embargo, cada operación de eliminación de la cola es equivalente a eliminar los datos con el subíndice 0 en la matriz, y los datos de toda la cola deben moverse, por lo que la complejidad temporal de la operación de eliminación de la cola cambiará desde el original O ( 1 ) O(1 $O\left(1\right)$ transforma$O\left(n\right)$ . ¿Se puede optimizar?

De hecho, no hay necesidad de mover datos al quitar la cola. Si no hay espacio libre, solo necesita activar una operación de movimiento de datos de forma centralizada al ingresar a la cola. Con esta idea, la función de poner en cola dequeue()permanece sin cambios, y una pequeña modificación de la implementación de la función de poner en cola enqueue()puede resolver fácilmente el problema en este momento. El siguiente es el código específico:

// 入队操作，将 item 放入队尾
public boolean enqueue(String item) {
    
    
    // tail == n 表示队列末尾没有空间了
    if (tail == n) {
    
    
        // tail ==n && head==0，表示整个队列都占满了
        if (head == 0) return false;
        // 数据搬移
        for (int i = head; i < tail; ++i) {
    
    
            items[i - head] = items[i];
        }
        // 搬移完之后重新更新 head 和 tail
        tail -= head;
        head = 0;
    }

    items[tail] = item;
    ++tail;
    return true;
}

Como se puede ver en el código, cuando el puntero de la cola de la cola se mueve hacia el extremo derecho de la matriz, si ingresan nuevos datos en la cola, los datos entre la cabeza y la cola se pueden mover a la posición de 0 a la cola en la matriz como un todo.

Veamos el método de implementación de la cola basada en listas enlazadas.La implementación basada en listas enlazadas también requiere dos punteros: el puntero principal y el puntero final. Apuntan al primer nodo y al último nodo de la lista enlazada respectivamente. Como se muestra en la figura, al entrar al equipo, cola -> siguiente = nuevo_nodo, cola = cola -> siguiente; al salir del equipo, cabeza = cabeza->siguiente

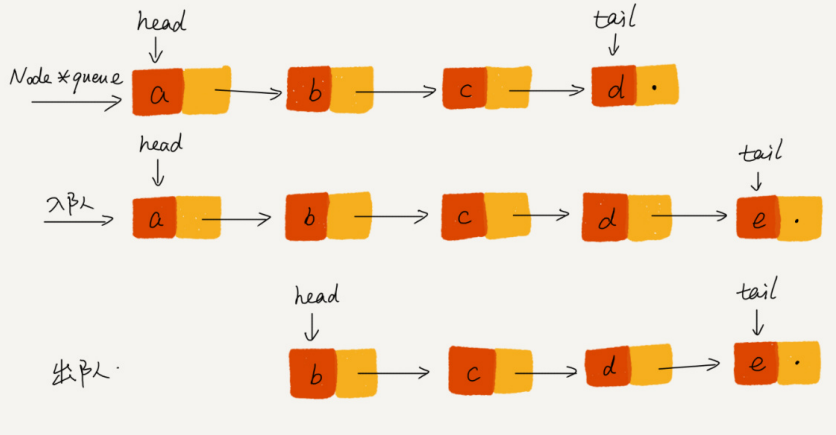
6.3 Cola circular

Cuando la matriz se usa para implementar la cola, cuando tail==n, habrá una operación de movimiento de datos, por lo que el rendimiento de la operación de puesta en cola se verá afectado. ¿Hay alguna forma de evitar la migración de datos? Echemos un vistazo a la solución a la cola circular.

Una cola circular, como sugiere su nombre, parece un anillo. La matriz original tiene una cabeza y una cola, que es una línea recta. Ahora conecte el extremo con el extremo para formar un anillo, como se muestra en la figura a continuación.

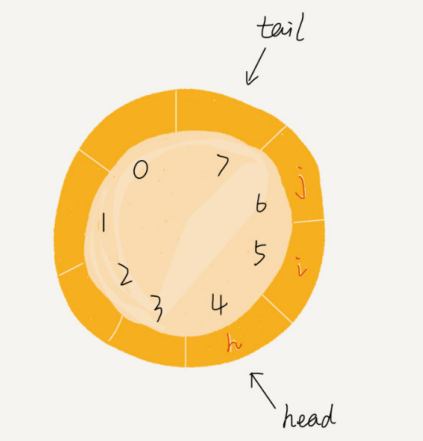
Se puede ver que el tamaño de la cola en la figura es 8, la cabeza actual = 4, la cola = 7. Cuando un nuevo elemento a ingrese a la cola, colóquelo en la posición con el subíndice 7. Pero en este momento, en lugar de actualizar la cola a 8, se mueve hacia atrás un bit en el anillo a la posición donde el subíndice es 0. Cuando otro elemento b ingrese a la cola, coloque b en la posición con el subíndice 0 y luego agregue 1 a la cola para actualizarlo a 1. Por lo tanto, después de que a y b se ponen en cola en secuencia, los elementos en la cola circular se convierten en los siguientes:

A través de este método, la operación de movimiento de datos se evita con éxito. No parece difícil de entender, pero la implementación del código de la cola circular es mucho más difícil que la cola no circular mencionada anteriormente. Si desea escribir el código de implementación de una cola circular sin errores, lo más importante es determinar las condiciones para juzgar si la cola está vacía o llena.

En una cola acíclica implementada por una matriz, la condición de evaluación para la cola llena es cola == n, y la condición de evaluación para la cola vacía es cabeza == cola. Para la cola circular, ¿cómo juzgar si la cola está vacía o llena?

La condición para juzgar que la cola está vacía sigue siendo cara == cruz. Pero las condiciones de evaluación para la cola completa son un poco más complicadas, como se muestra en la figura a continuación.

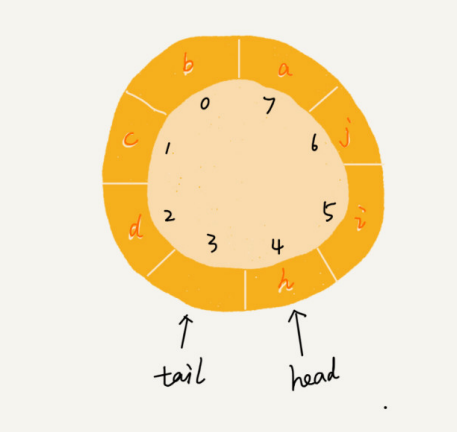
Al igual que la situación en la imagen donde el equipo está completo, cola = 3, cabeza = 4, n = 8, para resumir, la regla es: $(3+1)\%8=4$ . Haz algunos dibujos más del equipo completo y verás que cuando el equipo está completo,$(tail+1)\%n=cabeza\_\_\_$

En este momento, se encontrará que cuando la cola está llena, la ubicación señalada por la cola en la figura en realidad no almacena datos. Por lo tanto, la cola circular desperdiciará el espacio de almacenamiento de una matriz, el código es el siguiente:

public class CircularQueue {
    
    
    // 数组：items，数组大小：n
    private String[] items;
    private int n = 0;
    // head 表示队头下标，tail 表示队尾下标
    private int head = 0;
    private int tail = 0;
    // 申请一个大小为 capacity 的数组
    public CircularQueue(int capacity) {
    
    
        items = new String[capacity];
        n = capacity;
    }
    // 入队
    public boolean enqueue(String item) {
    
    
        // 队列满了
        if ((tail + 1) % n == head) return false;
        items[tail] = item;
        tail = (tail + 1) % n;
        return true;
    }
    // 出队
    public String dequeue() {
    
    
        // 如果 head == tail 表示队列为空
        if (head == tail) return null;
        String ret = items[head];
        head = (head + 1) % n;
        return ret;
    }
}

6.4 Bloqueo de colas y colas simultáneas

La cola de bloqueo en realidad está agregando operaciones de bloqueo sobre la base de la cola. En pocas palabras, cuando la cola está vacía, se bloqueará la obtención de datos desde el principio de la cola. Debido a que no hay datos disponibles en este momento, no puede regresar hasta que haya datos en la cola; si la cola está llena, la operación de insertar datos se bloqueará hasta que haya una posición libre en la cola antes de insertar datos y luego regresar

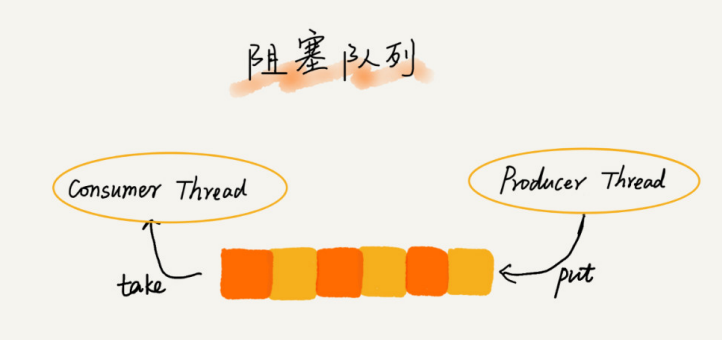
¡La definición anterior es en realidad un "modelo productor-consumidor"! ¡Usando colas de bloqueo, puede implementar fácilmente un "modelo productor-consumidor"!

Este "modelo productor-consumidor" basado en el bloqueo de colas puede coordinar efectivamente la velocidad de producción y consumo. Cuando el "productor" produce datos demasiado rápido y el "consumidor" no tiene tiempo para consumirlos, la cola para almacenar datos pronto estará llena. En este momento, el productor bloqueará y esperará hasta que el "consumidor" consuma los datos, y el "productor" se despertará para continuar con la "producción".

Y no solo eso, en función de la cola de bloqueo, la eficiencia del procesamiento de datos también se puede mejorar coordinando el número de "productores" y "consumidores". Por ejemplo, en el ejemplo anterior, puede configurar varios "consumidores" para tratar con un "productor"

En el caso de subprocesos múltiples, habrá varios subprocesos operando la cola al mismo tiempo. En este momento, habrá problemas de seguridad de subprocesos. ¿Cómo implementar una cola segura para subprocesos?

Una cola segura para subprocesos se denomina cola concurrente . El método de implementación más simple y directo es agregar bloqueos directamente a enqueue()los métodos dequeue(), pero la simultaneidad será relativamente baja si la granularidad del bloqueo es grande y solo se permite una operación de almacenamiento o recuperación al mismo tiempo. De hecho, las colas circulares basadas en arreglos pueden implementar colas concurrentes muy eficientes usando operaciones atómicas CAS. Esta es la razón por la que las colas circulares se usan más que las colas encadenadas.

6.5 Aplicación de colas en grupos de recursos limitados, como grupos de subprocesos

Los recursos de la CPU son limitados y la velocidad de procesamiento de las tareas no se correlaciona positivamente de forma lineal con la cantidad de subprocesos. Por el contrario, demasiados subprocesos provocarán cambios frecuentes de CPU y una disminución del rendimiento del procesamiento. Por lo tanto, el tamaño del grupo de subprocesos generalmente se establece de antemano considerando las características de la tarea a procesar y el entorno de hardware.

Al solicitar un subproceso de un grupo de subprocesos de tamaño fijo, si no hay recursos inactivos en el grupo de subprocesos, ¿cómo maneja el grupo de subprocesos esta solicitud en este momento? ¿Rechaza la solicitud o la pone en cola? ¿Cómo se implementan las diversas estrategias de procesamiento?

Generalmente, hay dos estrategias de tratamiento. El primero es un método de procesamiento sin bloqueo, que rechaza directamente la solicitud de tarea; el otro es un método de procesamiento de bloqueo, que pone en cola la solicitud y espera a que un subproceso inactivo elimine la solicitud en cola para continuar con el procesamiento. Entonces, ¿cómo se almacenan las solicitudes en cola?

Esperamos procesar cada solicitud en cola de manera justa, y las avanzadas se atenderán primero, por lo que la estructura de datos de la cola es muy adecuada para almacenar solicitudes en cola. Como se mencionó anteriormente, existen dos implementaciones de colas basadas en listas y matrices vinculadas. ¿Cuál es la diferencia entre estas dos implementaciones para las solicitudes en cola?

En función de la implementación de la lista vinculada, se puede implementar una cola ilimitada (cola ilimitada) que admita colas infinitas, pero puede hacer que demasiadas solicitudes esperen en línea y el tiempo de respuesta para el procesamiento de solicitudes sea demasiado largo. Por lo tanto, para los sistemas que son sensibles al tiempo de respuesta, un grupo de subprocesos en cola infinita basado en una lista vinculada no es adecuado

La cola limitada implementada en función de las matrices tiene un tamaño de cola limitado, por lo que cuando las solicitudes en cola en el grupo de subprocesos superan el tamaño de la cola, las solicitudes posteriores serán rechazadas. Este método es relativamente más razonable para los sistemas que son sensibles al tiempo de respuesta. Sin embargo, establecer un tamaño de cola razonable también es muy particular. Si la cola es demasiado grande, habrá demasiadas solicitudes en espera; si la cola es demasiado pequeña, no podrá utilizar completamente los recursos del sistema y maximizar el rendimiento.

Además de los escenarios mencionados anteriormente donde las colas se aplican a las solicitudes de cola en los grupos de subprocesos, las colas se pueden aplicar a cualquier grupo de recursos limitado para poner en cola las solicitudes, como los grupos de conexiones de bases de datos. De hecho, para la mayoría de los escenarios con recursos limitados, cuando no hay recursos inactivos, la estructura de datos de "cola" se puede usar básicamente para implementar la cola de solicitudes.

7. Recursividad

7.1 ¿Cómo entender "recursividad"?

Suponga que va al cine a ver una película y quiere saber en qué fila está sentado. Está demasiado oscuro dentro del cine, no puede ver con claridad, no puede contar, ¿qué debe hacer ahora?

Entonces, pregúntele a la persona en la primera fila en qué fila está, simplemente agregue uno a su número y sabrá en qué fila está. Sin embargo, la persona que estaba enfrente tampoco podía ver con claridad, por lo que también le preguntó a la persona que estaba frente a él. Simplemente pregunte fila por fila hasta que se le pregunte a la persona en la primera fila, diciendo que estoy en la primera fila, y luego pase el número fila por fila. Hasta que la persona que tienes delante te dice en qué fila está, entonces sabes la respuesta.

Este es un proceso de descomposición muy estándar de resolución recursiva de problemas. El proceso de ir se llama "recursión", y el proceso de regresar se llama "retorno". Básicamente, todos los problemas recursivos se pueden expresar mediante fórmulas recursivas. Para el ejemplo de ahora, expréselo con una fórmula recursiva como esta: $f\left(n\right)=f(norte-1)+1$ , donde$f\left(1\right)=1$

$f\left(n\right)$ significa que quieres saber en qué fila estás,$f(norte-1)$ indica el número de fila de la fila anterior,$f\left(1\right)=1$ significa que las personas en la primera fila saben que están en la primera fila. Con esta fórmula recursiva, se puede cambiar fácilmente a código recursivo, de la siguiente manera:

int f(int n) {
    
    
    if (n == 1) return 1;
    return f(n - 1) + 1;
}

7.2 Tres condiciones que deben cumplirse para la recursividad

El ejemplo anterior es una recursión muy típica, entonces, ¿qué tipo de problemas se pueden resolver con la recursión? Aquí se resumen tres condiciones, siempre que se cumplan las siguientes tres condiciones al mismo tiempo, se puede resolver mediante recursividad

1. La solución de un problema se puede descomponer en soluciones de varios subproblemas

¿Qué es un subproblema? Un subproblema es un problema con un tamaño de datos más pequeño. Por ejemplo, en el ejemplo del cine mencionado anteriormente, debe saber que la pregunta de "en qué fila se encuentra" se puede descomponer en el subproblema de "en qué fila está la persona de la fila anterior".

2. Este problema es el mismo que el subproblema después de la descomposición, excepto por la escala de datos, la idea de solución es exactamente la misma

Por ejemplo, en el ejemplo de una sala de cine, tu forma de pensar sobre "en qué fila estás" es exactamente la misma que la forma en que las personas en la primera fila se dan cuenta de "en qué fila estás".

3. Hay una condición de terminación recursiva

Descomponga el problema en subproblemas, luego descomponga los subproblemas en sub-subproblemas y descompóngalos capa por capa. No puede haber un ciclo infinito, lo que requiere una condición de terminación.

Todavía el ejemplo de una sala de cine, las personas en la primera fila saben en qué fila están sin preguntarle a nadie más, es decir, $f\left(1\right)=1$ , que es la condición de terminación para la recursividad

7.3 ¿Cómo escribir código recursivo?

La clave para escribir código recursivo es escribir la fórmula recursiva, encontrar la condición de terminación y convertir la fórmula recursiva en código es muy simple.

Suponiendo que hay n pasos aquí, uno o dos pasos se pueden cruzar cada vez, ¿cuántas maneras hay de caminar estos n pasos? Si hay 7 pasos, puede subir como 2, 2, 2, 1 o 1, 2, 1, 1, 2. En resumen, hay muchas formas de moverse, entonces, ¿cómo saber cuántas formas hay en total por programación?

Si lo piensa detenidamente, de hecho, todos los movimientos se pueden dividir en dos categorías según el primer paso. El primer tipo es que el primer paso es 1 paso, y el otro es que el primer paso es 2 pasos. Entonces, la forma de caminar n pasos es igual a la forma de caminar 1 paso primero, luego n-1 pasos más la forma de caminar 2 pasos primero, luego n-2 pasos. Expresado en una fórmula: $f\left(n\right)=f(norte-1)+f(norte-2)$

Con la fórmula recursiva, el código recursivo está básicamente a la mitad. Veamos de nuevo la condición de terminación. Cuando hay un paso, no hay necesidad de continuar con la recursividad, solo hay un camino a seguir. Entonces $f\left(1\right)=1$ . ¿Es esta condición de terminación recursiva suficiente? Puede experimentar con números relativamente pequeños como n=2 y n=3

n=2 时，$f\left(2\right)=f\left(1\right)+f\left(0\right)$ . Si la condición de terminación recursiva es solo una$f\left(1\right)=1$ , que$f\left(2\right)$ no se puede resolver. Así que en lugar de$f\left(1\right)=$Además de la condición de terminación recursiva de$1$$f\left(0\right)=1$ , lo que indica que hay una forma de caminar 0 pasos, pero esto parece ser inconsistente con el pensamiento lógico normal. Entonces, puedes poner$f\left(2\right)=2$ 作为一种终止条件，表示走 2 个台阶，有两种走法，一步走完或者分两步来走

所以，递归终止条件就是 $f(1)=1$，$f(2)=2$。这个时候，可以再拿 n=3，n=4 来验证一下，这个终止条件是否足够并且正确

把递归终止条件和刚刚得到的递推公式放到一起如下：

$$f(1)=1、f(2)=2、f(n)=f(n-1)+f(n-2)$$

有了这个公式，转化成递归代码就简单多了。最终的递归代码如下：

int f(int n) {
    
    
    if (n == 1) return 1;
    if (n == 2) return 2;
    return f(n - 1) + f(n - 2);
}

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码

El código recursivo es más difícil de entender, en el ejemplo de la sala de cine mencionado anteriormente, solo hay una rama de llamada recursiva, es decir, "un problema solo necesita ser descompuesto en un subproblema".

Sin embargo, cuando se enfrenta a un problema que debe descomponerse en múltiples subproblemas, el código recursivo no es tan fácil de entender.Como el segundo ejemplo anterior, el cerebro humano casi no tiene forma de pensar con claridad sobre todo el proceso de "recursión" y "recursión" paso a paso.

Las computadoras son buenas para hacer cosas repetitivas, por lo que la recursividad es perfecta para ellos. El cerebro humano prefiere una forma directa de pensar. Cuando vemos recurrencia, siempre queremos aplanar la recursión, y hacemos bucles en nuestra mente, ajustamos una capa a la vez y luego regresamos capa por capa, tratando de descubrir cómo se ejecuta cada paso de la computadora, para que sea fácil quedar atrapado en él.

Para el código recursivo, esta práctica de tratar de descifrar todo el proceso recursivo y recursivo es en realidad entrar en un malentendido del pensamiento. En muchos casos, nos cuesta entender, la razón principal es que nos hemos creado este tipo de barrera de comprensión. ¿Cuál debería ser la forma correcta de pensar?

Si un problema A se puede descomponer en varios subproblemas B, C y D, puede suponer que los subproblemas B, C y D se han resuelto y pensar en cómo resolver el problema A sobre esta base. Además, solo necesita pensar en la relación entre el problema A y los subproblemas B, C y D. No necesita pensar en la relación entre subproblemas y subproblemas, sub-subproblemas y sub-subproblemas. Enmascarar los detalles recursivos hace que sea más fácil de entender

Por lo tanto, la clave para escribir código recursivo es abstraerlo en una fórmula recursiva cada vez que encuentre una recursividad, sin pensar en la relación de llamadas capa por capa, y no intente usar el cerebro humano para descomponer cada paso de la recursividad.

7.4 Tenga cuidado con el desbordamiento de pila en código recursivo

En el desarrollo de software real, al escribir código recursivo, encontrará muchos problemas, como el desbordamiento de pila. El desbordamiento de la pila provocará un bloqueo del sistema, las consecuencias serán muy graves. ¿Por qué el código recursivo es propenso al desbordamiento de pila? ¿Y cómo evitar el desbordamiento de pila?

Como se mencionó en la sección "Pila", las llamadas a funciones usan la pila para almacenar variables temporales. Cada vez que se llama a una función, la variable temporal se encapsulará como un marco de pila y se insertará en la pila de memoria, y la pila no aparecerá hasta que la función regrese después de la ejecución. El espacio de la pila del sistema o de la máquina virtual generalmente no es grande. Si los datos que se van a resolver recursivamente tienen una gran escala y el nivel de llamada es muy profundo, y siempre se insertan en la pila, habrá riesgo de desbordamiento de la pila.

Por ejemplo, en el ejemplo de la sala de cine mencionado anteriormente, si la pila del sistema o el tamaño de la pila JVM se establece en 1 KB, al resolver $f\left(19999\right)$ , aparecerá el siguiente error de pila:

Excepción en el hilo "principal" java.lang.StackOverflowError

Entonces, ¿cómo evitar el desbordamiento de pila? Este problema se puede resolver limitando la profundidad máxima de las llamadas recursivas en el código. Después de que la llamada recursiva exceda una cierta profundidad (como 1000), no continuará recursiendo más y devolverá directamente un error

Pero este enfoque no puede resolver el problema por completo, porque la profundidad de recursión máxima permitida está relacionada con el espacio de pila restante del subproceso actual, que no se puede calcular de antemano. Si se calcula en tiempo real, el código es demasiado complejo, lo que afectará la legibilidad del código. Por lo tanto, si la profundidad máxima es relativamente pequeña, como 10, 50, puede usar este método; de lo contrario, este método no es muy práctico.

7.5 Tenga cuidado con la doble contabilidad en código recursivo

Además de esto, también existe el problema de la doble contabilidad cuando se utiliza la recursividad. El segundo ejemplo de código recursivo mencionado anteriormente, si todo el proceso recursivo se descompone, es así:

De la figura, se puede ver intuitivamente que queremos calcular $f\left(5\right)$ , necesito calcular f ( 4 ) f(4)primero$f\left(4\right)$ y$f\left(3\right)$ , mientras se calcula$f\left(4\right)$ también necesita calcular$f\left(3\right)$ , por lo tanto,$f\left(3\right)$ se calcula muchas veces, este es el problema de cálculo doble

Para evitar cálculos repetidos, se puede usar una estructura de datos (como una tabla hash) para guardar la solución $f\left(k\right)$ . Cuando la llamada recursiva a$f\left(k\right)$ , primero verifique si se ha resuelto. Si es así, devolverá el valor directamente de la tabla hash sin cálculos repetidos, por lo que se puede evitar el problema que acabamos de mencionar.

public int f(int n) {
    
    
    if (n == 1) return 1;
    if (n == 2) return 2;

    // hasSolvedList 可以理解成一个 Map，key 是 n，value 是 f(n)
    if (hasSolvedList.containsKey(n)) {
    
    
        return hasSovledList.get(n);
    }

    int ret = f(n - 1) + f(n - 2);
    hasSovledList.put(n, ret);
    return ret;
}

Además de los dos problemas comunes de desbordamiento de pila y conteo doble. Hay muchos otros problemas con el código recursivo

En términos de eficiencia de tiempo, hay muchas llamadas a funciones en el código recursivo. Cuando el número de estas llamadas a funciones es grande, se acumulará en un costo de tiempo considerable. En términos de complejidad de espacio, debido a que una llamada recursiva guardará los datos de campo una vez en la pila de memoria, al analizar la complejidad de espacio del código recursivo, se debe considerar esta parte de la sobrecarga. Por ejemplo, la complejidad de espacio del código recursivo del cine mencionado anteriormente no es O ( 1 ) O(1 $O\left(1\right)$ en lugar de$O\left(n\right)$

7.6 ¿Cómo reescribir código recursivo a código no recursivo?

La recursividad tiene ventajas y desventajas. La ventaja es que el código recursivo es muy expresivo y muy conciso para escribir. Las desventajas son la alta complejidad del espacio, el riesgo de desbordamiento de la pila, cálculos repetidos y llamadas a funciones excesivas que llevarán más tiempo. Por lo tanto, en el proceso de desarrollo, tenemos que elegir de acuerdo con la situación real si necesitamos implementarlo de forma recursiva.

¿Se puede reescribir el código recursivo como código no recursivo? Por ejemplo, en el ejemplo de la sala de cine de ahora, independientemente de la escena, solo mira $f\left(x\right)=f(x-1)+1$ Esta fórmula recursiva. Reescríbelo así:

int f(int n) {
    
    
    int ret = 1;
    for (int i = 2; i <= n; ++i) {
    
    
        ret = ret + 1;
    }
    return ret;
}

De manera similar, el segundo ejemplo también se puede cambiar a una implementación no recursiva

int f(int n) {
    
    
    if (n == 1) return 1;
    if (n == 2) return 2;

    int ret = 0;
    int pre = 2;
    int prepre = 1;
    for (int i = 3; i <= n; ++i) {
    
    
        ret = pre + prepre;
        prepre = pre;
        pre = ret;
    }
    return ret;
}

¿ Se pueden cambiar todos los códigos recursivos a escritura no recursiva de este bucle iterativo ?

En términos generales, sí. Porque la recursividad en sí se implementa con la ayuda de la pila, pero la pila utilizada la proporciona el sistema o la máquina virtual en sí, y no tenemos percepción. Si implementamos la pila en el montón de memoria y simulamos manualmente el proceso de empujar y sacar la pila, cualquier código recursivo se puede reescribir para que parezca código no recursivo.

Pero esta forma de pensar en realidad cambia la recursión a la recursión "manual", la esencia no ha cambiado y no resuelve algunos de los problemas mencionados anteriormente, lo que solo aumenta la complejidad de la implementación.

Veamos otro ejemplo, ahora, muchas aplicaciones tienen la función de recomendar descuentos en comisiones de registro, en esta función, el usuario A recomienda al usuario B que se registre y el usuario B recomienda al usuario C que se registre. Podemos decir que el "recomendador final" del usuario C es el usuario A, el "recomendador final" del usuario B también es el usuario A, y el usuario A no tiene un "recomendador final"

Generalmente, esta relación de recomendación se registra a través de una base de datos. En la tabla de la base de datos, se pueden registrar dos filas de datos, donde actor_id representa la identificación del usuario y referrer_id representa la identificación del recomendador.

Dado un ID de usuario, ¿cómo encuentro el "último remitente" para este usuario?

long findRootReferrerId(long actorId) {
    
    
    Long referrerId = select referrer_id from [table] where actor_id = actorId;
    if (referrerId == null) return actorId;
    return findRootReferrerId(referrerId);
}

¿Es muy conciso? Se puede hacer con tres líneas de código, pero en el proyecto real, el código anterior no funciona, ¿por qué? Hay dos problemas aquí

Primero, si la recursividad es profunda, puede haber un problema de desbordamiento de pila.

En segundo lugar, si hay datos sucios en la base de datos, es necesario lidiar con el problema de recursividad infinita resultante. Por ejemplo, en la base de datos en el entorno de demostración, el ingeniero de pruebas insertará artificialmente algunos datos para facilitar la prueba y aparecerán datos sucios. Si el recomendador de A es B, el recomendador de B es C y el recomendador de C es A, se producirá un bucle infinito.

El primer problema, como se mencionó anteriormente, puede resolverse limitando la profundidad de la recursividad. El segundo problema también se puede resolver limitando la profundidad de recursión. Sin embargo, existe un método de procesamiento más avanzado, que consiste en detectar automáticamente la existencia de "anillos" como ABCA

8. Ordenar

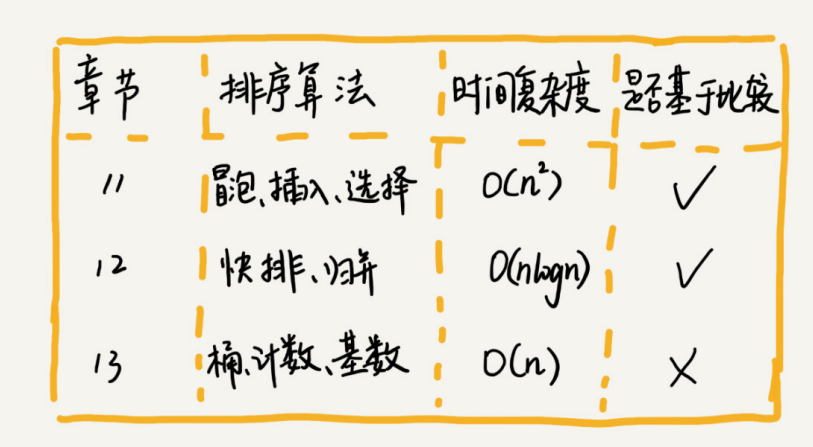
8.1 ¿Cómo analizar un "algoritmo de clasificación"?

Para aprender un algoritmo de clasificación, además de aprender su principio de algoritmo y la implementación del código, es más importante aprender a evaluar y analizar un algoritmo de clasificación. Luego analice un algoritmo de clasificación, ¿con qué aspectos deberíamos comenzar?

1. Eficiencia de ejecución del algoritmo de clasificación

El análisis de la eficiencia de ejecución del algoritmo de clasificación generalmente se mide a partir de los siguientes aspectos:

1. Complejidad temporal en el mejor de los casos, en el peor de los casos y en el caso promedio
   Al analizar la complejidad temporal de un algoritmo de ordenación, se debe proporcionar la complejidad temporal del mejor de los casos, el peor de los casos y el caso promedio, respectivamente. Además, también es necesario decir cuál es el dato original que se va a ordenar corresponde a la mejor y peor complejidad de tiempo

   ¿Por qué deberíamos distinguir entre estas tres complejidades temporales? En primer lugar, algunos algoritmos de clasificación distinguirán. Para comparar, es mejor hacer una distinción. En segundo lugar, para ordenar los datos, algunos están cerca del orden y otros están completamente desordenados. Los datos con diferentes grados de orden definitivamente tendrán un impacto en el tiempo de ejecución de la clasificación Necesitamos conocer el rendimiento de los algoritmos de clasificación bajo diferentes datos

2. Coeficientes, constantes y órdenes bajos de complejidad temporal La
   complejidad temporal refleja una tendencia de crecimiento cuando el tamaño de los datos n es grande, por lo que los coeficientes, las constantes y los órdenes bajos se ignoran cuando se expresan. Sin embargo, en el desarrollo de software real, se pueden ordenar datos a pequeña escala como 10, 100 y 1000. Por lo tanto, al comparar el rendimiento de los algoritmos de ordenación con el mismo orden de complejidad temporal, también se deben tener en cuenta los coeficientes, las constantes y los datos de bajo nivel.

3. El número de comparaciones e intercambios (o movimientos)
   El proceso de ejecución del algoritmo de clasificación basado en la comparación implica dos operaciones, una es la comparación de elementos y la otra es el intercambio o movimiento de elementos. Por lo tanto, al analizar la eficiencia de ejecución del algoritmo de clasificación, también se debe tener en cuenta el número de comparaciones y el número de intercambios (o movimientos).

2. Consumo de memoria del algoritmo de clasificación

El consumo de memoria de un algoritmo se puede medir por su complejidad de espacio, y los algoritmos de clasificación no son una excepción. Sin embargo, debido a la complejidad espacial del algoritmo de ordenación, se introduce un nuevo concepto, Sorted in place. El algoritmo de clasificación en el lugar se refiere específicamente al algoritmo de clasificación cuya complejidad espacial es O (1)

3. La estabilidad del algoritmo de clasificación.

No es suficiente medir la calidad de un algoritmo de clasificación solo por su eficiencia de ejecución y consumo de memoria. Para clasificar los algoritmos, existe otra métrica importante, la estabilidad. Este concepto significa que si hay elementos con valores iguales en la secuencia a clasificar, después de la clasificación, el orden original de los elementos iguales permanece sin cambios.

Por ejemplo, si hay un conjunto de datos 2, 9, 3, 4, 8, 3, después de ordenar por tamaño, será 2, 3, 3, 4, 8, 9. Hay dos 3 en este conjunto de datos. Después de ordenar por cierto algoritmo de clasificación, si el orden de los dos 3 no cambia, el algoritmo de clasificación se denomina algoritmo de clasificación estable; si el orden cambia, el algoritmo de clasificación correspondiente se denomina algoritmo de clasificación inestable

¿Qué importa cuál de los dos 3 está delante y cuál detrás?¿Qué importa si es estable o inestable? ¿Por qué debemos examinar la estabilidad del algoritmo de clasificación?

Muchos cursos de estructura de datos y algoritmos usan números enteros como ejemplos cuando se habla de clasificación, pero en el desarrollo de software real, lo que se debe clasificar a menudo no es un número entero simple, sino un conjunto de objetos, que deben clasificarse de acuerdo con una determinada clave del objeto.

比如说，现在要给电商交易系统中的“订单”排序。订单有两个属性，一个是下单时间，另一个是订单金额。如果现在有 10 万条订单数据，希望按照金额从小到大对订单数据排序。对于金额相同的订单，希望按照下单时间从早到晚有序。对于这样一个排序需求，怎么来做呢？

最先想到的方法是：先按照金额对订单数据进行排序，然后，再遍历排序之后的订单数据，对于每个金额相同的小区间再按照下单时间排序。这种排序思路理解起来不难，但是实现起来会很复杂

借助稳定排序算法，这个问题可以非常简洁地解决。解决思路是这样的：先按照下单时间给订单排序，注意是按照下单时间，不是金额。排序完成之后，用稳定排序算法，按照订单金额重新排序。两遍排序之后，得到的订单数据就是按照金额从小到大排序，金额相同的订单按照下单时间从早到晚排序的。为什么呢？

稳定排序算法可以保持金额相同的两个对象，在排序之后的前后顺序不变。第一次排序之后，所有的订单按照下单时间从早到晚有序了。在第二次排序中，用的是稳定的排序算法，所以经过第二次排序之后，相同金额的订单仍然保持下单时间从早到晚有序

8.2 冒泡排序（Bubble Sort）

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复 n 次，就完成了 n 个数据的排序工作

例如要对一组数据 4，5，6，3，2，1，从小到到大进行排序。第一次冒泡操作的详细过程就是这样：

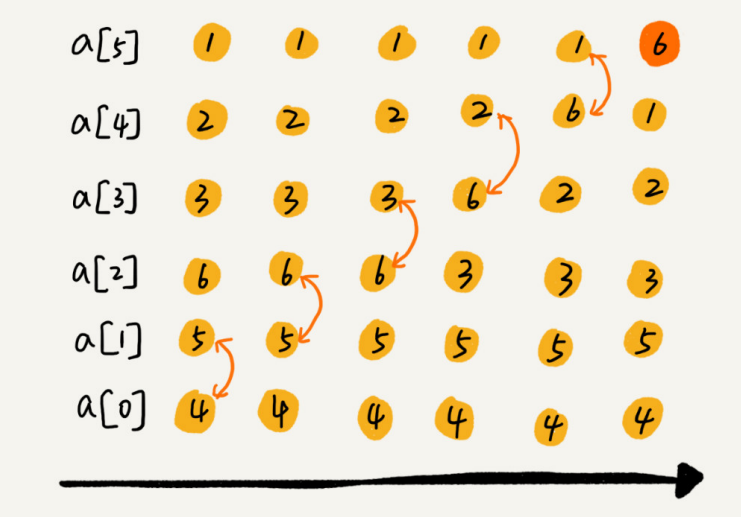
可以看出，经过一次冒泡操作之后，6 这个元素已经存储在正确的位置上。要想完成所有数据的排序，只要进行 6 次这样的冒泡操作就行了

实际上，上面的冒泡过程还可以优化。当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后续的冒泡操作。这里还有另外一个例子，这里面给 6 个元素排序，只需要 4 次冒泡操作就可以了

// 冒泡排序，a 表示数组，n 表示数组大小
public void bubbleSort(int[] a, int n) {
    
    
    if (n <= 1) return;
    for (int i = 0; i < n; ++i) {
    
    
        // 提前退出冒泡循环的标志位
        boolean flag = false;
        for (int j = 0; j < n - i - 1; ++j) {
    
    
            if (a[j] > a[j + 1]) {
    
     // 交换
                int tmp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = tmp;
                flag = true; // 表示有数据交换
            }
        }
        if (!flag) break; // 没有数据交换，提前退出
    }
}

现在，结合前面分析排序算法的三个方面，有三个问题

1. 冒泡排序是原地排序算法吗？

   El proceso de burbujeo solo implica la operación de intercambio de datos adyacentes y solo requiere un nivel constante de espacio temporal, por lo que su complejidad espacial es $O\left(1\right)$ , es un algoritmo de clasificación en el lugar

2. ¿Es Bubble Sort un algoritmo de clasificación estable?

   En el tipo de burbujas, solo el intercambio puede cambiar el orden de dos elementos. Para garantizar la estabilidad del algoritmo de clasificación de burbujas, cuando hay dos elementos adyacentes del mismo tamaño, no se realiza ningún intercambio y los datos del mismo tamaño no cambiarán el orden antes y después de la clasificación, por lo que la clasificación de burbujas es un algoritmo de clasificación estable.

3. ¿Cuál es la complejidad temporal del tipo de burbuja?

   En el mejor de los casos, los datos que se ordenarán ya están en orden y solo se necesita una operación de burbujeo para finalizar, por lo que la complejidad del tiempo en el mejor de los casos es O ( n ) $O\left(n\right)$ . En el peor de los casos, los datos que se ordenarán están en orden inverso, y se requieren n veces de operaciones burbujeantes, por lo que la complejidad de tiempo del peor de los casos es O ( n 2$O\left(n^2\right)$

   

La complejidad temporal de los mejores y peores casos es fácil de analizar, entonces, ¿cuál es la complejidad temporal del caso promedio? Como se mencionó anteriormente, la complejidad temporal promedio es la complejidad temporal esperada promedio ponderada, y el análisis debe combinarse con el conocimiento de la teoría de la probabilidad.

Para un arreglo que contiene n datos, hay n! tipos de arreglos para los n datos. Para diferentes arreglos, el tiempo de ejecución del tipo de burbuja debe ser diferente. Por ejemplo, en los dos ejemplos mencionados anteriormente, uno de ellos necesita 6 veces de burbujeo, mientras que el otro solo necesita 4 veces. Si la complejidad del tiempo promedio se analiza cuantitativamente por el método de la teoría de la probabilidad, el razonamiento matemático y el cálculo involucrados serán muy complicados. Aquí hay otra forma de pensar, a través de los dos conceptos de "grado de orden" y "grado de orden inverso" para analizar

El grado de orden es el número de pares de elementos que tienen una relación ordenada en el arreglo. Los pares ordenados de elementos se expresan matemáticamente así:

Par ordenado de elementos: a[i] <= a[j], si i < j

De manera similar, para una matriz en orden inverso, como 6, 5, 4, 3, 2, 1, el grado de orden es 0; para una matriz completamente ordenada, como 1, 2, 3, 4, 5, 6, el grado de orden es n ∗ ( n − 1 ) / 2 n * (n-1) / $norte\ast (n-1)/2$ , que es 15. El grado de orden de esta matriz completamente ordenada se denomina grado de orden completo

La definición de orden inverso es exactamente lo contrario del grado de orden (el valor predeterminado es el orden de menor a mayor)

Par de elementos en orden inverso: a[i] > a[j], si i < j

Respecto a estos tres conceptos, también se puede obtener una fórmula: grado de orden inverso = grado de orden completo - grado de orden . El proceso de clasificación es un proceso de aumentar el grado de orden y reducir el grado de orden inverso, y finalmente alcanzar el grado de orden completo significa que la clasificación se completa

Tomemos el ejemplo de clasificación de burbuja mencionado anteriormente para ilustrar. El estado inicial de la matriz a ordenar es 4, 5, 6, 3, 2, 1, donde los pares de elementos ordenados son (4, 5) (4, 6) (5, 6), por lo que el grado de ordenación es 3. n=6, por lo que el grado de orden completo del estado final después de la clasificación es $norte\ast (n-1)/2=15$

La clasificación de burbujas consta de dos átomos de operación, comparación e intercambio. El grado de orden aumenta en 1 cada vez que se intercambia. No importa cómo se mejore el algoritmo, siempre se determina el número de intercambios, que es el grado de orden inverso, es decir, $norte\ast (n-1)/2\; –Grado\; inicial\; de\; orden$ . En este ejemplo, es 15–3=12 y se requieren 12 operaciones de cambio

Para la clasificación de burbujas de una matriz que contiene n datos, ¿cuál es el número promedio de intercambios? En el peor de los casos, el grado de orden del estado inicial es 0, por lo que $norte\ast (n-1)/2$ permutas. En el mejor de los casos, el grado de orden del estado inicial es$norte\ast (n-1)/2$ , no hay necesidad de intercambio. Puede tomar un valor intermedio$norte\ast (n-1)/4$ , para representar el caso promedio donde el grado de orden inicial no es ni muy alto ni muy bajo

En otras palabras, en promedio, $norte\ast (n-1)/4$ operaciones de intercambio, la operación de comparación debe ser más que la operación de intercambio, y el límite superior de la complejidad es$O\left(n^2\right)$, por lo que la complejidad de tiempo promedio es$O\left(n^2\right)$

这个平均时间复杂度推导过程其实并不严格，但是很多时候很实用，毕竟概率论的定量分析太复杂，不太好用

8.3 插入排序（Insertion Sort）

先来看一个问题。一个有序的数组，往里面添加一个新的数据后，如何继续保持数据有序呢？很简单，只要遍历数组，找到数据应该插入的位置将其插入即可

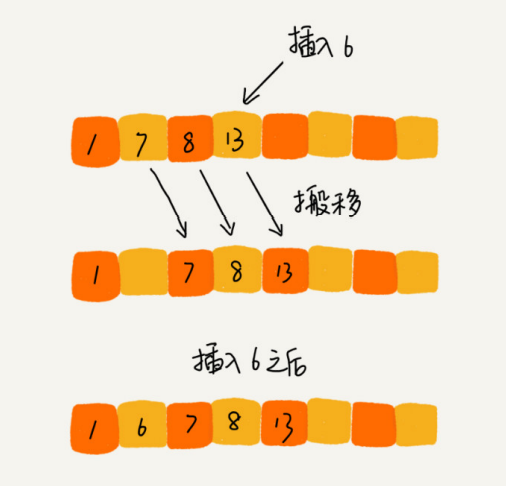
这是一个动态排序的过程，即动态地往有序集合中添加数据，可以通过这种方法保持集合中的数据一直有序。而对于一组静态数据，也可以借鉴上面讲的插入方法，来进行排序，于是就有了插入排序算法

那插入排序具体是如何借助上面的思想来实现排序的呢？

首先，将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束

如图所示，要排序的数据是 4，5，6，1，3，2，其中左侧为已排序区间，右侧是未排序区间

插入排序也包含两种操作，一种是元素的比较，一种是元素的移动。当需要将一个数据 a 插入到已排序区间时，需要拿 a 与已排序区间的元素依次比较大小，找到合适的插入位置。找到插入点之后，还需要将插入点之后的元素顺序往后移动一位，这样才能腾出位置给元素 a 插入

对于不同的查找插入点方法（从头到尾、从尾到头），元素的比较次数是有区别的。但对于一个给定的初始序列，移动操作的次数总是固定的，就等于逆序度

为什么说移动次数就等于逆序度呢？如下图，满有序度是 $n\ast (n-1)/2=15$，初始序列的有序度是 5，所以逆序度是 10。插入排序中，数据移动的个数总和也等于 10=3+3+4

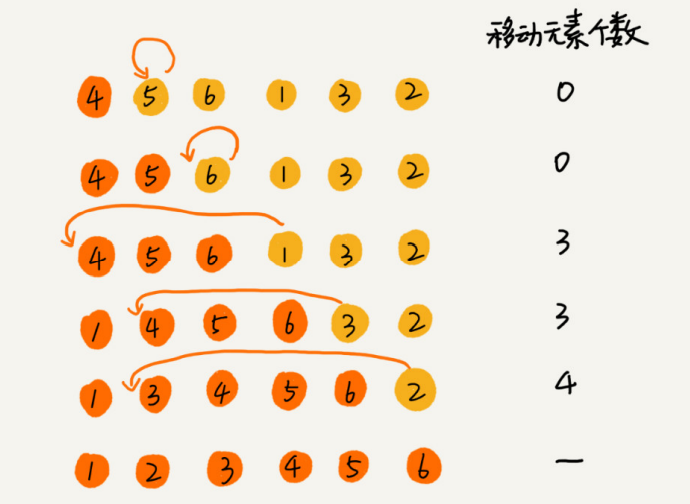
// 插入排序，a 表示数组，n 表示数组大小
public void insertionSort(int[] a, int n) {
    
    
    if (n <= 1) return;
    for (int i = 1; i < n; ++i) {
    
    
        int value = a[i];
        int j = i - 1;
        // 查找插入的位置
        for (; j >= 0; --j) {
    
    
            if (a[j] > value) {
    
    
                a[j + 1] = a[j]; // 数据移动
            } else {
    
    
                break;
            }
        }
        a[j + 1] = value; // 插入数据
    }
}

分析插入排序算法，同样有三个问题

1. 插入排序是原地排序算法吗？

   从实现过程可以很明显地看出，插入排序算法的运行并不需要额外的存储空间，所以空间复杂度是 $O(1)$，也就是说，这是一个原地排序算法

2. 插入排序是稳定的排序算法吗？

   在插入排序中，对于值相同的元素，可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法

3. 插入排序的时间复杂度是多少？

   如果要排序的数据已经是有序的，并不需要搬移任何数据。如果从尾到头在有序数据组里面查找插入位置，每次只需要比较一个数据就能确定插入的位置。所以这种情况下，最好是时间复杂度为 $O(n)$。注意，这里是从尾到头遍历已经有序的数据

   如果数组是倒序的，每次插入都相当于在数组的第一个位置插入新的数据，所以需要移动大量的数据，所以最坏情况时间复杂度为 $O(n^2)$

在数组中插入一个数据的平均时间复杂度是 $O\left(n\right)$ . Por lo tanto, para la ordenación por inserción, cada operación de inserción es equivalente a insertar un dato en la matriz, y el ciclo realiza n operaciones de inserción, por lo que la complejidad de tiempo promedio es$O\left(n^2\right)$

8.4 Clasificación de selección

La idea de implementación del algoritmo de ordenación por selección es algo similar a la ordenación por inserción, y también se divide en intervalos ordenados e intervalos no ordenados. Pero la ordenación por selección encontrará el elemento más pequeño del intervalo sin ordenar cada vez y lo colocará al final del intervalo ordenado.

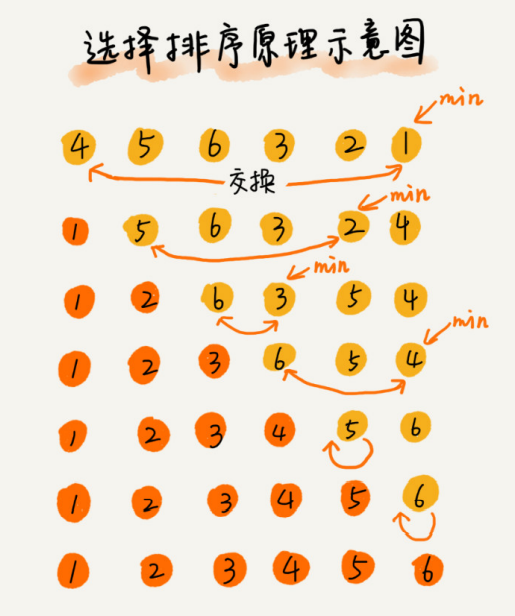
La complejidad del espacio de clasificación de selección es $O\left(1\right)$ , es un algoritmo de clasificación en el lugar. La complejidad de tiempo del mejor de los casos, la complejidad de tiempo del peor de los casos y la complejidad de tiempo del caso promedio del ordenamiento por selección son$O\left(n^2\right)$

¿Es la ordenación por selección un algoritmo de ordenación estable?

La respuesta es no, la clasificación por selección es un algoritmo de clasificación inestable. Como se puede ver en la figura anterior, la clasificación por selección debe encontrar el valor mínimo entre los elementos restantes sin clasificar cada vez e intercambiar posiciones con los elementos anteriores, lo que destruye la estabilidad.

Por ejemplo, si un grupo de datos como 5, 8, 5, 2 y 9 se clasifica mediante el algoritmo de clasificación por selección, el elemento 2 más pequeño se encuentra por primera vez y la posición se intercambia con los primeros 5, entonces el orden de los primeros 5 y los 5 del medio cambiará, por lo que será inestable. Debido a esto, la ordenación por selección es ligeramente inferior a la ordenación por burbujas y la ordenación por inserción.

¿Por qué la ordenación por inserción es más popular que la ordenación por burbujas?

La complejidad temporal de la ordenación por burbujas y la ordenación por inserción es $O\left(n^2\right)$Ambos son algoritmos de clasificación en el lugar ¿Por qué la clasificación por inserción es más popular que la clasificación por burbujas?

Al analizar la clasificación de burbujas y la clasificación por inserción, mencionamos que no importa cómo se optimice la clasificación de burbujas, la cantidad de intercambios de elementos es un valor fijo, que es el orden inverso de los datos originales. La clasificación por inserción es la misma, sin importar cuán optimizada esté, la cantidad de elementos movidos es igual al orden inverso de los datos originales

Sin embargo, desde la perspectiva de la implementación del código, el intercambio de datos de la clasificación por burbujas es más complicado que el movimiento de datos de la clasificación por inserción. La clasificación por burbujas requiere tres operaciones de asignación, mientras que la clasificación por inserción solo necesita una. Fíjate en esta operación:

冒泡排序中数据的交换操作：
if (a[j] > a[j + 1]) {
    
     // 交换
    int tmp = a[j];
    a[j] = a[j + 1];
    a[j + 1] = tmp;
    flag = true;
}
插入排序中数据的移动操作：
if (a[j] > value) {
    
    
    a[j + 1] = a[j]; // 数据移动
} else {
    
    
    break;
}

El tiempo para ejecutar una instrucción de asignación se calcula aproximadamente como unidad de tiempo (unit_time), y luego se utiliza la clasificación por burbujas y la clasificación por inserción para clasificar la misma matriz con un orden inverso de K. La clasificación de burbujas requiere K veces de operaciones de intercambio, cada una de las cuales requiere 3 sentencias de asignación, por lo que el tiempo total dedicado a las operaciones de intercambio es 3*K unidad de tiempo. Sin embargo, la operación de movimiento de datos en ordenación por inserción solo necesita K unidad de tiempo

Este es solo un análisis muy teórico. En aras de la experimentación, escribí un programa de prueba de comparación de rendimiento para los códigos Java anteriores de clasificación de burbujas y clasificación por inserción, generando aleatoriamente 10,000 matrices, cada una con 200 datos, y luego usé los algoritmos de clasificación de burbujas e inserción para clasificar en mi máquina. ¡El algoritmo de clasificación de burbujas tarda aproximadamente 700 ms en completarse, mientras que la clasificación por inserción solo toma alrededor de 100 ms en completarse!

Entonces, aunque la ordenación por burbuja y la ordenación por inserción tienen la misma complejidad de tiempo, ambas son $O\left(n^2\right)$, pero si desea lograr la máxima optimización del rendimiento, la ordenación por inserción es definitivamente la primera opción. La idea del algoritmo de ordenación por inserción también tiene mucho espacio para la optimización.. El anterior es solo el más básico. Si está interesado en la optimización de la ordenación por inserción, puede aprender la ordenación de Hill usted mismo

8.5 Clasificación por fusión

Si desea ordenar una matriz, primero divida la matriz en partes delantera y trasera desde el medio, luego ordene las partes delantera y trasera por separado, y luego combine las dos partes ordenadas, de modo que la matriz completa esté en orden.

Merge sort utiliza la idea de divide y vencerás. Divide y vencerás, como su nombre indica, es dividir y vencer, descomponiendo un gran problema en pequeños subproblemas a resolver. Cuando se resuelven los pequeños subproblemas, también se resuelve el gran problema.

La idea de divide y vencerás es muy similar a la idea recursiva mencionada anteriormente. Los algoritmos de divide y vencerás generalmente se implementan mediante recursividad. Divide y vencerás es una idea de procesamiento para resolver problemas, y la recursividad es una técnica de programación, y las dos no entran en conflicto. A continuación, echemos un vistazo a cómo usar el código recursivo para implementar la ordenación por combinación

El truco para escribir código recursivo es analizar la fórmula recursiva, luego encontrar la condición de terminación y finalmente traducir la fórmula recursiva a código recursivo. Por lo tanto, si desea escribir el código para la ordenación por fusión, primero escriba la fórmula recursiva para la ordenación por fusión

Fórmula recursiva: merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
Condición de terminación: p >= r No es necesario continuar con la descomposición

merge_sort(p…r) significa ordenar la matriz con subíndices de p a r. Transforme este problema de clasificación en dos subproblemas, merge_sort(p...q) y merge_sort(q+1...r), donde el subíndice q es igual a la posición media de p y r, es decir, ( p + r ) / 2 (p+r)/ $(pag+r)/2$ . Después de ordenar los dos subarreglos con subíndices de p a q y de q+1 a r, fusione los dos subarreglos ordenados, de modo que los datos entre los subíndices de p a r también se ordenen. La traducción a pseudocódigo es la siguiente:

// 归并排序算法, A 是数组，n 表示数组大小
merge_sort(A, n) {
    
    
    merge_sort_c(A, 0, n-1)
}
// 递归调用函数
merge_sort_c(A, p, r) {
    
    
    // 递归终止条件
    if p >= r then return
    // 取 p 到 r 之间的中间位置 q
    q = (p+r) / 2
    // 分治递归
    merge_sort_c(A, p, q)
    merge_sort_c(A, q+1, r)
    // 将 A[p...q] 和 A[q+1...r] 合并为 A[p...r]
    merge(A[p...r], A[p...q], A[q+1...r])
}

merge(A[p…r], A[p…q], A[q+1…r]) La función de esta función es fusionar el orden A[p…q] y A[q+1…r] en una matriz ordenada y ponerlo en A[p…r]. Entonces, ¿cómo se debe hacer este proceso?

Como se muestra en la figura, solicite una matriz temporal tmp con el mismo tamaño que A[p…r]. Use dos cursores i y j, apuntando al primer elemento de A[p…q] y A[q+1…r] respectivamente. Compare estos dos elementos A[i] y A[j], si A[i]<=A[j], coloque A[i] en la matriz temporal tmp y mueva i un poco hacia atrás; de lo contrario, coloque A[j] en la matriz tmp y mueva j un bit hacia atrás

Continúe con el proceso de comparación anterior hasta que todos los datos de uno de los subconjuntos se coloquen en el conjunto temporal y, a continuación, agregue los datos del otro conjunto al final del conjunto temporal. En este momento, lo que se almacena en el conjunto temporal es el resultado de fusionar los dos subconjuntos. Finalmente, copie los datos en la matriz temporal tmp a la matriz original A[p...r]

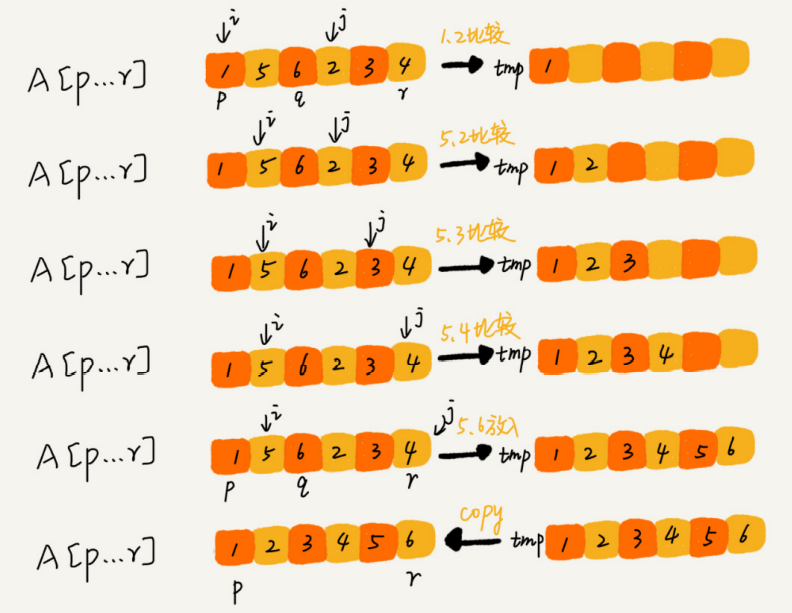
Escriba merge()la función como pseudocódigo, que es como sigue:

merge(A[p...r], A[p...q], A[q + 1...r]) {
    
    
    var i : = p，j : = q + 1，k : = 0 // 初始化变量 i, j, k
    var tmp : = new array[0...r - p] // 申请一个大小跟 A[p...r] 一样的临时数组
    while i <= q AND j <= r do {
    
    
        if A[i] <= A[j] {
    
    
        	tmp[k++] = A[i++] // i++ 等于 i:=i+1
        } else {
    
    
        	tmp[k++] = A[j++]
    	}
    }

    // 判断哪个子数组中有剩余的数据
    var start : = i，end : = q
    if j <= r then start : = j, end: = r
	// 将剩余的数据拷贝到临时数组 tmp
    while start <= end do {
    
    
    	tmp[k++] = A[start++]
    }

    // 将 tmp 中的数组拷贝回 A[p...r]
    for i : = 0 to r - p do {
    
    
    	A[p + i] = tmp[i]
    }
}

1. ¿Es merge sort un algoritmo de clasificación estable?

La clave para la estabilidad e inestabilidad de la ordenación por fusión depende de merge()la función, es decir, la parte del código que fusiona dos subarreglos ordenados en una matriz ordenada Durante el proceso de fusión, si hay elementos con el mismo valor entre A[p…q] y A[q+1…r], primero puede colocar los elementos en A[p…q] en la matriz tmp como en el pseudocódigo. Esto asegura que los elementos con el mismo valor estén en el mismo orden antes y después de la fusión. Por lo tanto, merge sort es un algoritmo de clasificación estable

2. ¿Cuál es la complejidad temporal de la ordenación por fusión?

La ordenación por combinación implica recursividad, y el análisis de la complejidad del tiempo es un poco complicado. El escenario aplicable de recursividad es que un problema a puede descomponerse en múltiples subproblemas b y c, luego resolver el problema a puede descomponerse en resolver los problemas b y c. Después de resolver los problemas b y c, fusionamos los resultados de b y c en el resultado de a

Si definimos el tiempo para resolver el problema a como $T\left(a\right)$ , el tiempo para resolver los problemas b y c son respectivamente$T\left(b\right)$ y$T\left(c\right)$ , entonces puedo obtener la relación de recurrencia:$T\left(un\right)=T\left(b\right)+T\left(c\right)+K$ , donde K es igual al tiempo que lleva combinar los resultados de los dos subproblemas b y c en el resultado del problema a

Del análisis anterior, se puede sacar una conclusión importante: no solo el problema de solución recursiva se puede escribir como una fórmula recursiva, sino que también la complejidad temporal del código recursivo se puede escribir como una fórmula recursiva . Aplique esta fórmula para analizar la complejidad temporal de la ordenación por fusión

Suponga que el tiempo requerido para fusionar y clasificar n elementos es $T\left(n\right)$ , el tiempo para descomponerse en dos subarreglos es$T(n/\; 2)$ . merge()La complejidad temporal de la función para fusionar dos subarreglos ordenados es$O\left(n\right)$ . Por tanto, aplicando la fórmula anterior, la fórmula de cálculo de la complejidad temporal del merge sort es:

T(1) = C; cuando n=1, solo se requiere un tiempo de ejecución de nivel constante, por lo que se expresa como C
T(n) = 2 * T(n/2) + n; n>1

A través de esta fórmula, cómo resolver $¿Qué\; pasa\; con\; T\left(n\right)$ ? ¿No es lo suficientemente intuitivo? Luego, analicemos aún más el proceso de cálculo.

T(n) = 2 * T(n/2) + n
= 2 *(2 * T(n/4) + n/2) + n = 4 * T(n/4) + 2 * n = 4 * (2 * T(n/8) + n/4) + 2 * n = 8 * T(n/8) + 3 * n = 8 *( 2 * T(n/16) + n/8) + 3 * n = 16 * T(n/16) + 4 * n... = 2^k * T(n/2^k)
+
k
*
n
...

Al descomponer y derivar paso a paso, podemos obtener $T\left(n\right)=2^{k}T(n/2^k)+kn$。当 $T(n/2^k)=Cuando\; T\left(1\right)$ , eso es$n/2^k=1$ , obtener$k=registro\_{\_}_{}norte$ _ Sustituyendo el valor de k en la fórmula anterior se obtiene$T\left(n\right)=Cnorte+nlog\_{}_{}norte$ _ En notación O grande,$T\left(n\right)$ es igual a$O\left(nregistron\right)$ .$\_$$\_$Entonces, la complejidad de tiempo de la ordenación por fusión es$O\left(nlogn\right)\_\_$

Se puede ver a partir del análisis principal y el pseudocódigo que la eficiencia de ejecución de la ordenación por combinación no tiene nada que ver con el grado de ordenación de la matriz original que se ordenará, por lo que su complejidad de tiempo es muy estable, sin importar si es el mejor de los casos, el peor de los casos o el caso promedio, la complejidad de tiempo es O (nlogn) O(nlogn $O\left(nlogn\right)\_\_$

3. ¿Cuál es la complejidad espacial de la ordenación por fusión?

La complejidad temporal del ordenamiento por fusión es $O\left(nlogn\right),$ se ve bastante bien$.$Incluso con ordenación rápida, en el peor de los casos, la complejidad del tiempo es$O\left(n^2\right)$. Sin embargo, la ordenación por combinación no se usa tanto como la ordenación rápida. Debido a que tiene una "debilidad" fatal, es decir, la clasificación por fusión no es un algoritmo de clasificación en el lugar.

这是因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。那归并排序的空间复杂度到底是多少呢？是 $O(n)$，还是 $O(nlogn)$，应该如何分析呢？

如果继续按照分析递归时间复杂度的方法，通过递推公式来求解，那整个归并过程需要的空间复杂度就是 $O(nlogn)$。不过，类似分析时间复杂度那样来分析空间复杂度，这个思路对吗？

实际上，递归代码的空间复杂度并不能像时间复杂度那样累加。刚刚忘记了最重要的一点，那就是，尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 $O(n)$

8.6 快速排序（Quick Sort）

快排利用的也是分治思想。乍看起来，它有点像归并排序，但是思路其实完全不一样

La idea central de la ordenación rápida: si desea ordenar un conjunto de datos con subíndices de p a r en la matriz, seleccione cualquier dato entre p y r como pivote (punto de partición)

Recorra los datos entre p y r, coloque los datos más pequeños que el pivote a la izquierda, coloque los datos más grandes que el pivote a la derecha y coloque el pivote en el medio. Después de este paso, los datos entre la matriz p y r se dividen en tres partes, la parte frontal entre p y q-1 es más pequeña que el pivote, la parte central es el pivote y la parte entre q+1 y r es más grande que el pivote.

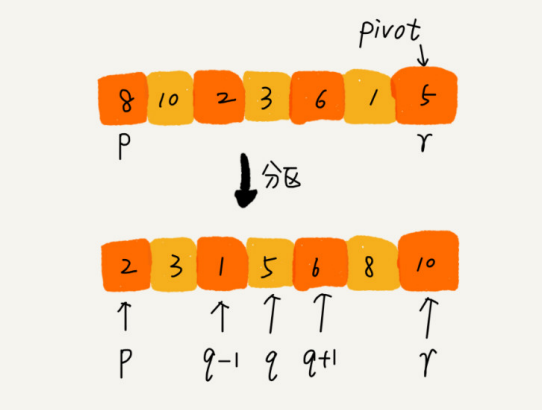
De acuerdo con la idea de divide y vencerás y el procesamiento recursivo, puedes ordenar recursivamente los datos con subíndices de p a q-1 y los datos con subíndices de q+1 a r hasta que el intervalo se reduzca a 1, lo que significa que todos los datos están en orden

Si el proceso anterior se escribe con una fórmula recursiva, es así:

递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1, r)
终止条件：
p >= r

Convierta la fórmula recursiva en código recursivo:

// 快速排序，A 是数组，n 表示数组的大小
quick_sort(A, n) {
    
    
 quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数，p,r 为下标
quick_sort_c(A, p, r) {
    
    
 if p >= r then return
 
 q = partition(A, p, r) // 获取分区点
 quick_sort_c(A, p, q-1)
 quick_sort_c(A, q+1, r)
}

En la ordenación por fusión hay una merge()función de fusión, aquí hay una partition()función de partición. partition()De hecho, la función de partición ya se mencionó anteriormente, que consiste en seleccionar aleatoriamente un elemento como pivote (en general, puede elegir el último elemento en el intervalo de p a r), y luego dividir A[p...r], y la función devuelve el subíndice de pivote

Si no se considera el consumo de espacio, partition()la función de partición se puede escribir de manera muy simple. Solicite dos matrices temporales X e Y, recorra A[p...r], copie los elementos más pequeños que el pivote en la matriz temporal X, copie los elementos más grandes que el pivote en la matriz temporal Y y finalmente copie los datos en la matriz X y la matriz Y en A[p...r]

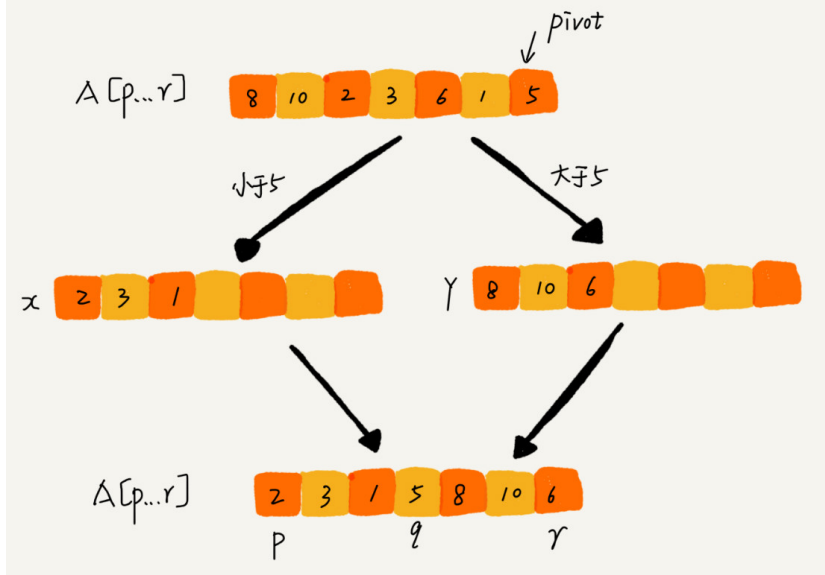
Sin embargo, si se implementa de acuerdo con esta idea, partition()la función requerirá mucho espacio de memoria adicional, por lo que Quicksort no es un algoritmo de clasificación en el lugar. Si desea que quicksort sea un algoritmo de clasificación en el lugar, entonces su complejidad de espacio debe ser O(1), entonces la partition()función de partición no puede ocupar demasiado espacio de memoria adicional y debe completar la operación de partición en lugar de A[p...r]

La idea de implementación de la función de partición in situ es muy ingeniosa, y el pseudocódigo es el siguiente:

partition(A, p, r) {
    
    
  pivot := A[r]
  i := p
  for j := p to r-1 do {
    
    
    if A[j] < pivot {
    
    
      swap A[i] with A[j]
      i := i+1
    }
  }
  swap A[i] with A[r]
  return i
 }

El procesamiento aquí es algo similar a la ordenación por selección. Dividimos A[p…r-1] en dos partes por el cursor i. Los elementos de A[p…i-1] son ​​todos más pequeños que el pivote, lo llamamos “intervalo procesado” por ahora, y A[i…r-1] es “intervalo no procesado”. Cada vez que tomamos un elemento A[j] del intervalo sin procesar A[i...r-1], lo comparamos con el pivote, si es más pequeño que el pivote, luego lo agregamos al final del intervalo procesado, que es la posición de A[i]

Insertar un elemento en una determinada posición en la matriz requiere mover datos, lo que lleva mucho tiempo. Pero también hablamos de una técnica de procesamiento, es decir, el intercambio, y la operación de inserción se completa dentro de la complejidad temporal de O(1). Aquí también usamos esta idea, solo necesitamos intercambiar A[i] y A[j], podemos poner A[j] en la posición del subíndice i dentro de la complejidad de tiempo O(1)

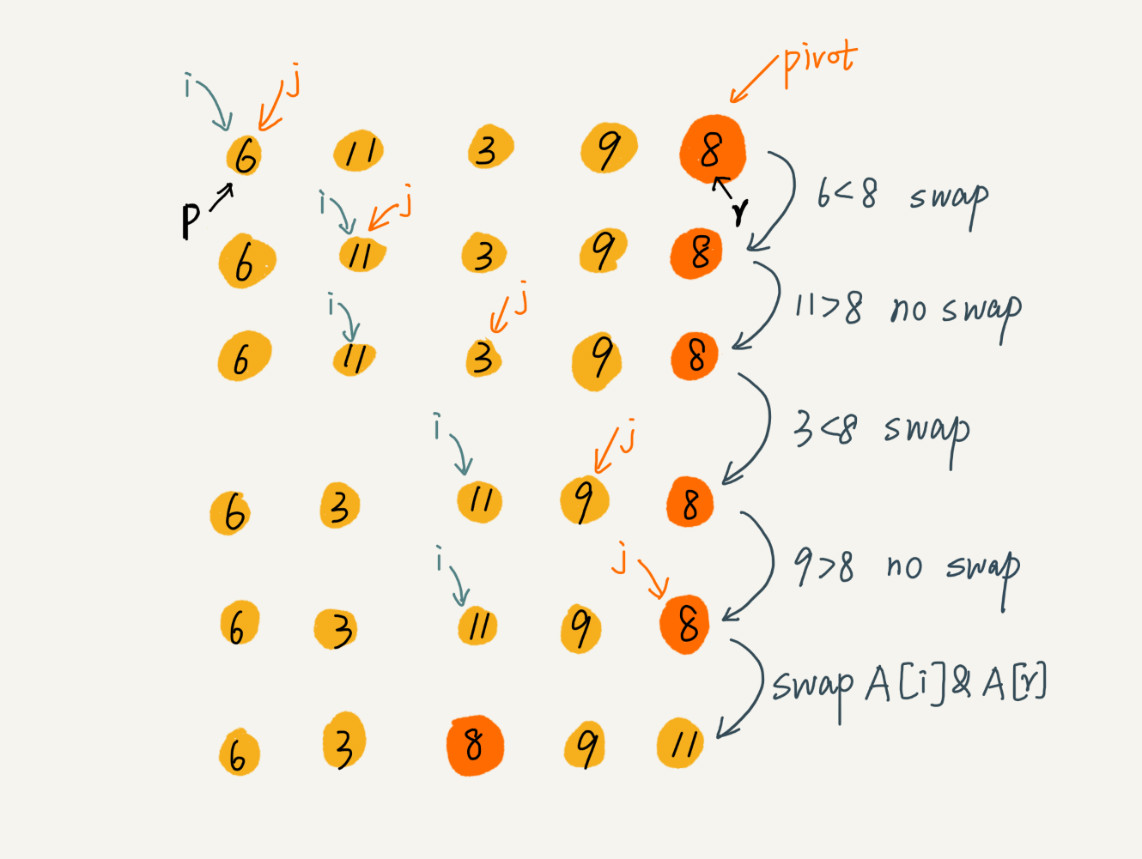
Debido a que el proceso de partición involucra operaciones de intercambio, si hay dos elementos idénticos en la matriz, como la secuencia 6, 8, 7, 6, 3, 5, 9, 4, después de la primera operación de partición, el orden relativo de los dos 6 cambiará. Por lo tanto, quicksort no es un algoritmo de clasificación estable

Análisis de rendimiento de Quick Sort

Quicksort también se implementa mediante recursividad. Para la complejidad temporal del código recursivo, la fórmula resumida anteriormente sigue siendo aplicable aquí. Si cada operación de partición puede simplemente dividir la matriz en dos áreas pequeñas con tamaños casi iguales, entonces la fórmula de solución recursiva de complejidad temporal de clasificación rápida es la misma que la de combinación. Por lo tanto, la complejidad temporal de la clasificación rápida también es O(nlogn)

T(1) = C；   n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = 2*T(n/2) + n； n>1

Sin embargo, la premisa de la fórmula es que para cada operación de partición, el pivote que elegimos es muy adecuado, que puede dividir el intervalo grande en dos por igual. Pero en la práctica, esta situación es difícil de lograr.

Tomemos un ejemplo extremo. Si los datos en la matriz ya están ordenados, como 1, 3, 5, 6, 8. Si elegimos el último elemento como pivote cada vez, los dos intervalos obtenidos por cada partición no son iguales. Necesitamos realizar alrededor de n operaciones de partición para completar todo el proceso de clasificación rápida. En cada partición, necesitamos escanear alrededor de n/2 elementos en promedio. En este caso, la complejidad de tiempo de ordenación rápida degenera de O(nlogn) a O (n 2) $O\left(n^2\right)$

Acabo de hablar sobre la complejidad temporal de dos casos extremos, uno es que la partición está extremadamente equilibrada y el otro es que la partición está extremadamente desequilibrada. Corresponden a la complejidad de tiempo en el mejor de los casos y la complejidad de tiempo en el peor de los casos de clasificación rápida, respectivamente. ¿Cuál es la complejidad de tiempo promedio de la clasificación rápida?

Suponga que cada operación de partición divide el intervalo en dos pequeños intervalos con un tamaño de 9:1. Si continuamos aplicando la fórmula recursiva de complejidad temporal recursiva, quedará así:

T(1) = C;  n=1 时，只需要常量级的执行时间，所以表示为 C。
 
T(n) = T(n/10) + T(9*n/10) + n； n>1

El proceso de resolución recursiva de esta fórmula es muy complicado, aunque se puede resolver, no se recomienda este método. De hecho, además de la fórmula recursiva, el método recursivo de solución de complejidad temporal también tiene un árbol recursivo. Aquí hay una conclusión directa para usted: T (n) puede lograr una complejidad de tiempo O (nlogn) en la mayoría de los casos, y solo en casos extremos degenerará a O (n 2) O (n ^ 2 $O\left(n^2\right)$. Además, también tenemos muchas formas de reducir esta probabilidad a un nivel muy bajo.

Tanto quicksort como merge usan la idea de divide y vencerás, y la fórmula recursiva y el código recursivo también son muy similares, entonces, ¿cuál es la diferencia entre ellos?

Se puede encontrar que el proceso de procesamiento de clasificación por combinación es de abajo hacia arriba , primero procesando subproblemas y luego fusionando. La clasificación rápida es todo lo contrario, su proceso de procesamiento es de arriba a abajo , primero se divide y luego se procesan los subproblemas. Aunque merge sort es un algoritmo de clasificación estable con una complejidad de tiempo de O(nlogn), es un algoritmo de clasificación fuera de lugar. Como dijimos anteriormente, la razón principal por la que merge es un algoritmo de clasificación fuera de lugar es que la función merge no se puede ejecutar en su lugar. La clasificación rápida puede lograr la clasificación en el lugar mediante el diseño de ingeniosas funciones de partición en el lugar, lo que resuelve el problema de la combinación y la clasificación que ocupan demasiada memoria.

¿Cómo encontrar el K-ésimo elemento más grande en una matriz sin clasificar en una complejidad de tiempo O (n)?

La idea central de Quicksort es dividir y conquistar y particionar Podemos usar la idea de partición para responder a esta pregunta: encuentre el K-ésimo elemento más grande en la matriz desordenada en complejidad de tiempo O(n). Por ejemplo, para un conjunto de datos como 4, 2, 5, 12, 3, el tercer elemento más grande es 4

Seleccionamos el último elemento A[n-1] del intervalo del arreglo A[0…n-1] como pivote, y dividimos el arreglo A[0…n-1] in situ, de modo que el arreglo se divida en tres partes, A[0…p-1], A[p], A[p+1…n-1]

Si p+1=K, entonces A[p] es el elemento a resolver; si K>p+1, significa que el K-ésimo elemento más grande aparece en el intervalo de A[p+1…n-1], y buscamos recursivamente en el intervalo de A[p+1…n-1] de acuerdo con las ideas anteriores. De manera similar, si K<p+1, entonces buscamos en el intervalo A[0…p-1]

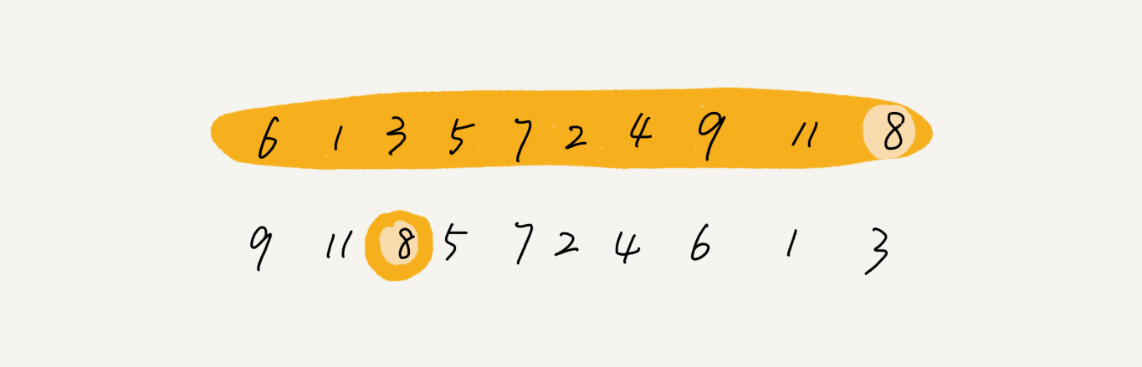
Mirémoslo de nuevo, ¿por qué la complejidad temporal de las soluciones anteriores es O(n)?

Para la primera búsqueda de partición, necesitamos realizar una operación de partición en una matriz de tamaño n, y necesitamos recorrer n elementos. Para la búsqueda de la segunda partición, solo necesitamos realizar una operación de partición en una matriz de tamaño n/2, y necesitamos atravesar n/2 elementos. Por analogía, el número de elementos transversales de partición son, respectivamente, n/2, n/4, n/8, n/16... hasta que el intervalo se reduce a 1

Si sumamos el número de elementos atravesados ​​por cada partición, es: n+n/2+n/4+n/8+...+1. Esta es una suma de una secuencia geométrica, y la suma final es igual a 2n-1. Por lo tanto, la complejidad temporal de la solución anterior es O(n)

Podría decir, tengo una manera estúpida de tomar el valor mínimo en la matriz cada vez, moverlo al frente de la matriz y luego continuar encontrando el valor mínimo en la matriz restante, y así sucesivamente, ejecutar K veces, ¿no son los datos encontrados el K-ésimo elemento más grande?

Sin embargo, la complejidad del tiempo no es O(n), sino O(K * n). Podrías decir, ¿no es insignificante el coeficiente frente a la complejidad del tiempo? ¿No es O(K * n) igual a O(n)?

Esto no puede ser tan simple. Cuando K es una constante relativamente pequeña, como 1, 2, la mejor complejidad temporal es de hecho O(n); pero cuando K es igual a n/2 o n, la peor complejidad temporal es O ( n 2 ) O(n^2 $O\left(n^2\right)$arriba

9. Clasificación lineal

Hay tres algoritmos de ordenación cuya complejidad temporal es O(n): ordenación por cubo, ordenación por conteo y ordenación por base. Debido a que la complejidad temporal de estos algoritmos de clasificación es lineal, llamamos a este tipo de algoritmo de clasificación Clasificación lineal . La razón principal por la que se puede lograr la complejidad del tiempo lineal es que estos tres algoritmos son algoritmos de clasificación no basados ​​en comparación y no implican operaciones de comparación entre elementos.

9.1 Clasificación de cubos

La clasificación de cubos, como su nombre indica, utiliza "cubos". La idea central es dividir los datos que se clasificarán en varios cubos ordenados y luego clasificar los datos en cada cubo por separado. Después de ordenar los cubos, los datos de cada cubo se extraen en secuencia y la secuencia formada está en orden

¿Por qué la complejidad temporal de la clasificación de cubetas es O(n)?

Si hay n datos para ordenar, los dividimos uniformemente en m cubos, y hay k = n/m elementos en cada cubo. La ordenación rápida se usa dentro de cada cubo y la complejidad de tiempo es O(k * logk). La complejidad temporal de clasificar m cubetas es O(m * k * logk), porque k=n/m, por lo que la complejidad temporal de clasificar la cubeta completa es O(n*log(n/m)). Cuando el número m de cubos está cerca del número n de datos, log(n/m) es una constante muy pequeña. En este momento, la complejidad temporal de la clasificación de cubos está cerca de O(n)

La clasificación de cubos se ve muy bien, entonces, ¿puede reemplazar el algoritmo de clasificación del que hablamos antes?

La respuesta es, por supuesto, no. De hecho, la clasificación de cubos es muy exigente con los datos que se van a clasificar.

En primer lugar, los datos que se ordenarán deben dividirse fácilmente en cubos m, y hay un orden natural de tamaño entre cubos. De esta manera, después de ordenar los datos en cada depósito, no es necesario ordenar los datos entre depósitos.

En segundo lugar, la distribución de datos entre cubos es relativamente uniforme. Si después de dividir los datos en cubos, algunos cubos contienen una gran cantidad de datos, algunos son muy pequeños y muy desiguales, entonces la complejidad del tiempo para clasificar los datos en el cubo no es constante. En casos extremos, si todos los datos se dividen en un depósito, se degenera en un algoritmo de clasificación O (nlogn)

La clasificación de cubos es más adecuada para la clasificación externa . La llamada clasificación externa significa que los datos se almacenan en un disco externo. La cantidad de datos es relativamente grande y la memoria es limitada. Es imposible cargar todos los datos en la memoria.

Por ejemplo, tenemos 10 GB de datos de pedido y queremos ordenar por el monto del pedido (suponiendo que el monto sea un número entero positivo), pero nuestra memoria es limitada, solo unos pocos cientos de MB, y no hay forma de cargar todos los 10 GB de datos en la memoria al mismo tiempo. ¿Qué debemos hacer en este momento?

Podemos escanear el archivo primero para ver el rango de datos del monto del pedido. Supongamos que después de escanear, obtenemos que el monto mínimo del pedido es de 1 yuan y el máximo es de 100 000 yuan. Dividimos todos los pedidos en 100 cubos según la cantidad. En el primer cubo almacenamos pedidos con un monto entre 1 yuan y 1000 yuanes, en el segundo cubo almacenamos pedidos con un monto entre 1001 yuanes y 2000 yuanes, y así sucesivamente. Cada balde corresponde a un archivo, y está numerado y nombrado de acuerdo al tamaño del rango de cantidad (00, 01, 02...99)

Idealmente, si el monto del pedido se distribuye uniformemente entre 10 000 y 100 000, el pedido se dividirá uniformemente en 100 archivos, y cada archivo pequeño almacenará alrededor de 100 MB de datos del pedido. Podemos poner estos 100 archivos pequeños en la memoria uno por uno y usar la ordenación rápida para ordenarlos. Después de ordenar todos los archivos, solo necesitamos leer los datos del pedido en cada archivo pequeño en orden de acuerdo con el número de archivo de menor a mayor, y escribirlos en un archivo, luego este archivo almacena los datos del pedido ordenados por la cantidad de menor a mayor

Sin embargo, los pedidos no se distribuyen necesariamente de manera uniforme según la cantidad entre 1 yuan y 100 000 yuanes, por lo que los datos del pedido de 10 GB no se pueden dividir de manera uniforme en 100 archivos. Es posible que haya una gran cantidad de datos en un cierto rango de cantidad, y el archivo correspondiente será muy grande después de la división, que no se puede leer en la memoria al mismo tiempo. ¿Qué debemos hacer?

Para los archivos que aún son relativamente grandes después de estas divisiones, podemos continuar dividiéndolos. Por ejemplo, si el monto del pedido está entre 1 yuan y 1000 yuanes, continuaremos dividiendo este rango en 10 áreas pequeñas, 1 yuan a 100 yuanes, 101 yuanes a 200 yuanes, 201 yuanes a 300 yuanes ... 901 yuanes a 1000 yuanes. Si después de dividir, todavía hay demasiados pedidos entre 101 yuanes y 200 yuanes para leerlos en la memoria al mismo tiempo, continúe dividiendo hasta que todos los archivos puedan leerse en la memoria

9.2 Clasificación por conteo

La ordenación por conteo es en realidad un caso especial de ordenación por cubo . Cuando el rango de n datos a ordenar no es grande, por ejemplo, el valor máximo es k, podemos dividir los datos en k cubos. Los valores de datos en cada cubo son los mismos, lo que ahorra el tiempo de clasificación en el cubo

Todos hemos experimentado el examen de ingreso a la universidad ¿Recuerdas el sistema de calificación del examen de ingreso a la universidad? Cuando comprobemos la puntuación, el sistema mostrará nuestra puntuación y el ranking de la provincia en la que nos encontramos. Si hay 500.000 candidatos en tu provincia, ¿cómo obtener el ranking a través de una ordenación rápida de resultados?

El puntaje total de los candidatos es 900 y el mínimo es 0. El rango de estos datos es muy pequeño, por lo que podemos dividirlo en 901 cubos, correspondientes a puntajes de 0 a 900. Según las puntuaciones de los candidatos, dividimos los 500.000 candidatos en estos 901 cubos. Los datos de los cubos son candidatos con la misma puntuación, por lo que no es necesario volver a ordenarlos. Solo necesitamos escanear cada cubo por turno, y generar los candidatos en el cubo en una matriz por turno, y se realiza la clasificación de 500,000 candidatos. Debido a que solo están involucradas las operaciones de exploración transversal, la complejidad del tiempo es O (n)

La idea del algoritmo de clasificación por conteo es tan simple que es muy similar a la clasificación por cubetas, excepto que el tamaño y la granularidad de las cubetas son diferentes. Pero, ¿por qué este algoritmo de clasificación se llama clasificación de "recuento"? ¿De dónde viene el significado de "contar"?

Para entender este problema, tenemos que mirar la implementación del algoritmo de clasificación por conteo. Tome al alumno como ejemplo para explicar. Suponga que solo hay 8 candidatos con puntajes entre 0 y 5. Ponemos las puntuaciones de estos 8 candidatos en una matriz A[8], son: 2, 5, 3, 0, 2, 3, 0, 3

Las calificaciones de los candidatos van de 0 a 5, y usamos una matriz C[6] con un tamaño de 6 para representar los cubos, donde los subíndices corresponden a las puntuaciones. Sin embargo, lo que se almacena en C[6] no son candidatos, sino el número correspondiente de candidatos. Como en el ejemplo que acabo de dar, solo necesitamos iterar las puntuaciones de los candidatos para obtener el valor de C[6]

En la figura se puede ver que hay 3 candidatos con una puntuación de 3 y 4 candidatos con una puntuación inferior a 3. Por lo tanto, los candidatos con una puntuación de 3 guardarán las posiciones de los subíndices 4, 5 y 6 en la matriz ordenada ordenada R[8]

Entonces, ¿cómo calculamos rápidamente la ubicación de almacenamiento correspondiente de los candidatos para cada puntaje en la matriz ordenada? Este enfoque es muy inteligente.

Sumamos secuencialmente la matriz C[6], y los datos almacenados en C[6] se convierten en los siguientes. C[k] almacena el número de candidatos cuya puntuación es menor o igual a k

Escaneamos la matriz A secuencialmente de atrás hacia adelante. Por ejemplo, al escanear a 3, podemos sacar el valor 7 con el subíndice 3 de la matriz C, es decir, hasta ahora, incluyéndome, hay 7 candidatos cuya puntuación es menor o igual a 3, es decir, 3 es el séptimo elemento de la matriz R (es decir, la posición con el subíndice 6 en la matriz R). Cuando se coloca 3 en la matriz R, solo hay 6 elementos menores o iguales a 3, por lo que el C[3] correspondiente debe reducirse en 1 para convertirse en 6

Por analogía, cuando escaneamos el segundo candidato con una puntuación de 3, lo colocaremos en la posición del sexto elemento en la matriz R (es decir, la posición con el subíndice 5). Cuando escaneamos toda la matriz A, los datos en la matriz R se organizan en orden de menor a mayor según la puntuación.

el código se muestra a continuación:

// 计数排序，a 是数组，n 是数组大小。假设数组中存储的都是非负整数。
public void countingSort(int[] a, int n) {
    
    
  if (n <= 1) return;
 
  // 查找数组中数据的范围
  int max = a[0];
  for (int i = 1; i < n; ++i) {
    
    
    if (max < a[i]) {
    
    
      max = a[i];
    }
  }
 
  int[] c = new int[max + 1]; // 申请一个计数数组 c，下标大小 [0,max]
  for (int i = 0; i <= max; ++i) {
    
    
    c[i] = 0;
  }
 
  // 计算每个元素的个数，放入 c 中
  for (int i = 0; i < n; ++i) {
    
    
    c[a[i]]++;
  }
 
  // 依次累加
  for (int i = 1; i <= max; ++i) {
    
    
    c[i] = c[i-1] + c[i];
  }
 
  // 临时数组 r，存储排序之后的结果
  int[] r = new int[n];
  // 计算排序的关键步骤，有点难理解
  for (int i = n - 1; i >= 0; --i) {
    
    
    int index = c[a[i]]-1;
    r[index] = a[i];
    c[a[i]]--;
  }
 
  // 将结果拷贝给 a 数组
  for (int i = 0; i < n; ++i) {
    
    
    a[i] = r[i];
  }
}

¿No es muy inteligente esta implementación de usar otra matriz para contar? Esta es la razón por la cual este algoritmo de clasificación se llama clasificación por conteo.

La ordenación por conteo solo se puede usar en escenarios donde el rango de datos no es grande. Si el rango de datos k es mucho más grande que los datos que se ordenarán n, no es adecuado usar la ordenación por conteo. Además, la ordenación por conteo solo puede ordenar números enteros no negativos. Si los datos a ordenar son de otro tipo, deben convertirse en un número entero no negativo sin cambiar el tamaño relativo.

Tomemos el ejemplo de los estudiantes. Si el puntaje del examinado tiene una precisión de un decimal, debemos multiplicar todos los puntajes por 10, convertirlos en números enteros y luego colocarlos en cubos 9010. Para otro ejemplo, si hay números negativos en los datos que se ordenarán y el rango de los datos es [-1000, 1000], entonces debemos agregar 1000 a cada dato para convertirlo en un número entero no negativo.

9.3 Clasificación por Radix

Supongamos que tenemos 100 000 números de teléfonos móviles y queremos clasificar estos 100 000 números de teléfonos móviles de menor a mayor. ¿Tiene algún método de clasificación más rápido?

La ordenación rápida de la que hablamos antes puede lograr una complejidad de tiempo O(nlogn) ¿Existe un algoritmo de ordenación más eficiente? ¿Pueden ser útiles la clasificación de baldes y la clasificación por conteo? El número de teléfono móvil tiene 11 dígitos y el rango es demasiado grande, por lo que obviamente no es adecuado para estos dos algoritmos de clasificación. Para este problema de clasificación, ¿hay algún algoritmo cuya complejidad temporal sea O(n)?

Hay una regla de este tipo en la pregunta de ahora: suponga que desea comparar el tamaño de dos números de teléfono móvil a y b, si en los primeros dígitos, el número de teléfono móvil de a ya es más grande que el número de teléfono móvil de b, entonces no necesita mirar los últimos dígitos

Con la ayuda del algoritmo de clasificación estable, aquí hay una idea de implementación inteligente. Primero ordene los números de teléfonos móviles según el último dígito, luego reordene según el penúltimo dígito, y así sucesivamente, y finalmente reordene según el primer dígito. Después de 11 clases, los números de teléfono están todos en orden.

Tenga en cuenta que si el algoritmo de clasificación para clasificar por bits es estable, de lo contrario, esta idea de implementación es incorrecta. Porque si es un algoritmo de clasificación inestable, la última clasificación solo considerará el orden de tamaño del bit más alto, independientemente de la relación de tamaño de otros bits, entonces la clasificación de bit bajo no tiene ningún sentido

Para ordenar de acuerdo con cada bit, podemos usar el ordenamiento por cubo o el ordenamiento por conteo que acabamos de mencionar, y su complejidad de tiempo puede ser O(n). Si los datos a clasificar tienen k bits, entonces necesitamos k tiempos de clasificación de cubos o clasificación de conteo, y la complejidad de tiempo total es O(k*n). Cuando k no es grande, como en el ejemplo de la clasificación de números de teléfonos móviles, el k máximo es 11, por lo que la complejidad temporal de la clasificación radix es aproximadamente O(n)

De hecho, a veces los datos a ordenar no tienen todos la misma longitud, por ejemplo, cuando ordenamos las 200.000 palabras en inglés en el diccionario de Oxford, la más corta tiene solo 1 letra y la más larga 45 letras. Para tales datos de longitud desigual, ¿sigue siendo aplicable la ordenación radix?

De hecho, podemos llenar todas las palabras con la misma longitud, y si no hay suficientes dígitos, podemos agregar "0" al final, porque según el valor ASCII, todas las letras son mayores que "0", por lo que agregar "0" no afectará el orden original de tamaño. De esta manera, puede continuar usando la clasificación radix

La clasificación por cardinalidad tiene requisitos para que los datos se clasifiquen. Debe poder separar "bits" independientes para la comparación, y existe una relación progresiva entre los bits. Si el bit alto de un dato es mayor que el dato b, entonces los bits bajos restantes no necesitan compararse. Además, el rango de datos de cada bit no debe ser demasiado grande, y el algoritmo de clasificación lineal se puede usar para clasificar; de lo contrario, la complejidad temporal de la clasificación radix no puede ser O (n)

¿Cómo ordenar 1 millón de usuarios por edad?

De hecho, clasificar 1 millón de usuarios por edad es como clasificar 500 000 examinados por grado. Suponemos que el rango de edades va desde un mínimo de 1 año hasta un máximo de 120 años. Podemos recorrer los 1 millón de usuarios, dividirlos en los 120 cubos según la edad y luego recorrer los elementos en los 120 cubos en secuencia. Esto nos da un conjunto de datos de 1 millón de usuarios ordenados por edad.

¿Cómo implementar una función de clasificación genérica de alto rendimiento?

¿Cómo elegir un algoritmo de clasificación adecuado?

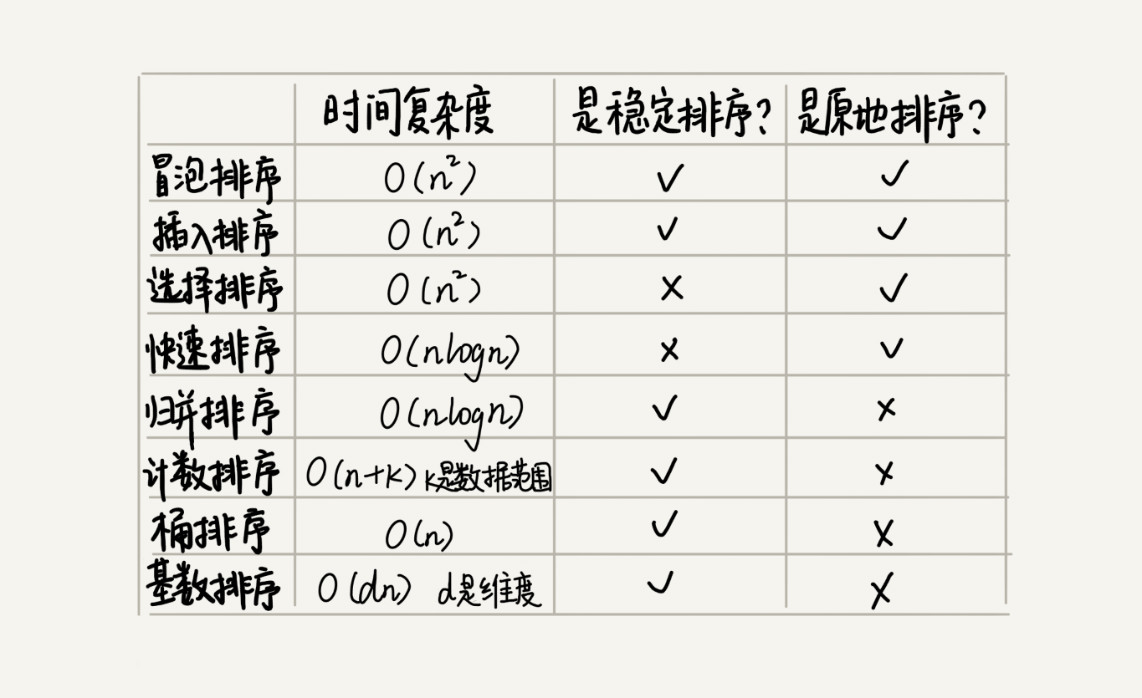
La complejidad temporal del algoritmo de clasificación lineal es relativamente baja y los escenarios aplicables son relativamente especiales. Entonces, si desea escribir una función de clasificación general, no puede elegir el algoritmo de clasificación lineal

Si ordena datos a pequeña escala, puede elegir que la complejidad del tiempo sea $O\left(n^2\right)$algoritmo; si se clasifican datos a gran escala, el algoritmo con complejidad de tiempo O (nlogn) es más eficiente. Por lo tanto, para tener en cuenta la clasificación de datos de cualquier escala, generalmente se prefiere un algoritmo de clasificación con una complejidad de tiempo de O (nlogn) para implementar la función de clasificación.

La complejidad del tiempo es O(nlogn). Hay más de un algoritmo de ordenación, como la ordenación por combinación, la ordenación rápida y la ordenación en montón. Tanto la clasificación en montón como la clasificación rápida tienen más aplicaciones. Por ejemplo, el lenguaje Java usa la clasificación en montón para implementar funciones de clasificación, y el lenguaje C usa la clasificación rápida para implementar funciones de clasificación.

No sé si ha descubierto que no hay muchos casos en los que se utilice la ordenación por fusión. Sabemos que la complejidad temporal de ordenación rápida en el peor de los casos es $O\left(n^2\right)$, y la ordenación por combinación puede alcanzar la complejidad temporal de O(nlogn) en el caso promedio y en el peor de los casos. Desde este punto de vista, parece muy atractivo, entonces, ¿por qué no ha sido "favorecido"?

La ordenación por combinación no es un algoritmo de ordenación en el lugar y su complejidad espacial es O(n). Entonces, en términos generales, si desea clasificar 100 MB de datos, además de la memoria ocupada por los datos en sí, el algoritmo de clasificación ocupará 100 MB adicionales de espacio de memoria y el consumo de espacio se duplicará.

La clasificación rápida es más adecuada para implementar funciones de clasificación, pero también sabemos que la complejidad temporal de la clasificación rápida en el peor de los casos es $O\left(n^2\right)$¿Cómo resolver este problema de "deterioro de la complejidad"?

¿Cómo optimizar Quicksort?

Primero veamos por qué la complejidad temporal de la clasificación rápida en el peor de los casos es $O\left(n^2\right)$¿Sobre qué? Como se mencionó anteriormente, si los datos están originalmente ordenados o casi ordenados, y se seleccionan los últimos datos para cada punto de partición, el algoritmo de clasificación rápida será muy malo y la complejidad del tiempo degenerará a O ( n 2 ) O(n^2$O\left(n^2\right)$. En realidad,este$O\left(n^2\right)$La razón principal de la aparición de la complejidad del tiempo es que nuestra selección de particiones no es lo suficientemente razonable

Entonces, ¿qué tipo de punto de partición es un buen punto de partición? ¿O cómo elegir el punto de partición?

最理想的分区点是：被分区点分开的两个分区中，数据的数量差不多

如果很粗暴地直接选择第一个或者最后一个数据作为分区点，不考虑数据的特点，肯定会出现之前讲的那样，在某些情况下，排序的最坏情况时间复杂度是 $O(n^2)$。为了提高排序算法的性能，我们也要尽可能地让每次分区都比较平均

这里介绍两个比较常用、比较简单的分区算法

1、三数取中法

我们从区间的首、尾、中间，分别取出一个数，然后对比大小，取这 3 个数的中间值作为分区点。这样每间隔某个固定的长度，取数据出来比较，将中间值作为分区点的分区算法，肯定要比单纯取某一个数据更好。但是，如果要排序的数组比较大，那“三数取中”可能就不够了，可能要“五数取中”或者“十数取中”

2、随机法

随机法就是每次从要排序的区间中，随机选择一个元素作为分区点。这种方法并不能保证每次分区点都选的比较好，但是从概率的角度来看，也不大可能会出现每次分区点都选的很差的情况，所以平均情况下，这样选的分区点是比较好的。时间复杂度退化为最糟糕的 $O(n^2)$ 的情况，出现的可能性不大

快速排序是用递归来实现的。递归要警惕堆栈溢出。为了避免快速排序里，递归过深而堆栈过小，导致堆栈溢出，我们有两种解决办法：第一种是限制递归深度。一旦递归过深，超过了我们事先设定的阈值，就停止递归。第二种是通过在堆上模拟实现一个函数调用栈，手动模拟递归压栈、出栈的过程，这样就没有了系统栈大小的限制

举例分析排序函数

Tome la función en Glibc qsort()como ejemplo. Aunque qsort()por el nombre, parece estar basado en el algoritmo de ordenación rápida, de hecho no solo usa el algoritmo de ordenación rápida

Si observa el código fuente, encontrará que qsort()la clasificación por fusión se usará primero para clasificar los datos de entrada , porque la complejidad del espacio de la clasificación por fusión es O(n), por lo que para clasificar volúmenes de datos pequeños, como 1 KB, 2 KB, etc., la clasificación por fusión requiere 1 KB o 2 KB adicionales de espacio de memoria, lo cual no es un gran problema. Hoy en día la memoria de los ordenadores es bastante grande, y lo que muchas veces perseguimos es la velocidad

Pero si la cantidad de datos es demasiado grande, como mencionamos anteriormente, clasificar 100 MB de datos no es apropiado para nosotros en este momento. Por lo tanto, cuando la cantidad de datos a clasificar es relativamente grande, qsort()se clasificará mediante el algoritmo de clasificación rápida

Entonces, qsort()¿cómo elegir el punto de partición del algoritmo de clasificación rápida? Si observa el código fuente, encontrará que qsort()el método para seleccionar puntos de partición es el "método de tres números"

También existe el problema de que la recursión demasiado profunda causará el desbordamiento de la pila que mencionamos anteriormente, qsort()que se resuelve implementando una pila en el montón y simulando manualmente la recursión.

De hecho, qsort()no solo se utilizan la ordenación por fusión y la ordenación rápida, sino que también utiliza la ordenación por inserción. En el proceso de ordenación rápida, cuando el número de elementos en el intervalo a ordenar es menor o igual a 4, se qsort()degenera en ordenación por inserción, y no se sigue usando la recursividad para la ordenación rápida, porque también hemos dicho antes que ante datos a pequeña escala, O ( n 2 ) $O\left(n^2\right)$Los algoritmos con complejidad temporal no son necesariamente más largos que los algoritmos O(nlogn). Analicemos ahora esta afirmación

Cuando hablamos de análisis de complejidad, dijimos que el rendimiento del algoritmo se puede analizar a través de la complejidad del tiempo, sin embargo, este tipo de análisis de complejidad es más teórico, si profundizamos, la complejidad del tiempo no es igual al tiempo real de ejecución del código.

La complejidad del tiempo representa una tendencia de crecimiento. Si dibuja una curva de crecimiento, encontrará $O\left(n^2\right)$Es más inclinado que O(nlogn), lo que significa que la tendencia de crecimiento es más fuerte. Sin embargo, como dijimos antes, en la notación de gran complejidad O, omitiremos los coeficientes y constantes de bajo orden, es decir, O(nlogn) puede ser O(knlogn + c) antes de que se omitan los coeficientes y constantes de bajo orden, y k y c aún pueden ser un número relativamente grande

Supongamos que k=1000, c=200, cuando ordenamos datos a pequeña escala (como n=100), ${norte}^{El\; valor\; de\; 2}$ es en realidad menor que knlogn+c

knlogn+c = 1000 * 100 * log100 + 200 远大于 10000
 
n^2 = 100*100 = 10000

Entonces, para la clasificación de datos a pequeña escala, $O\left(n^2\right)$El algoritmo de clasificación no requiere necesariamente más tiempo para ejecutarse que el algoritmo de clasificación O(nlogn). Para la clasificación de pequeños volúmenes de datos, elegimos un algoritmo de clasificación de inserción relativamente simple que no requiere recursividad.

El centinela mencionado anteriormente simplifica el código y mejora la eficiencia de ejecución. qsort()Esta técnica de programación también se utiliza en la implementación del algoritmo de clasificación por inserción . Aunque el centinela puede hacer un juicio menos, después de todo, la función de clasificación es una función muy común y básica, y la optimización del rendimiento debe ser extrema.

10. Búsqueda binaria

Algoritmo de búsqueda para conjuntos de datos ordenados: algoritmo de búsqueda binaria (búsqueda binaria), también conocido como algoritmo de búsqueda binaria

10.1 El pensamiento dicotómico es ubicuo

La búsqueda binaria es un algoritmo de búsqueda rápida muy simple y fácil de entender, que se puede ver en todas partes en la vida. Por ejemplo, en el clásico juego de adivinanzas de palabras, escriba al azar un número entre 0 y 99 y luego adivine lo que está escrito. Durante el proceso de adivinanza, cada vez que adivine, se le preguntará si la conjetura es más grande o más pequeña, hasta que acierte.

Suponiendo que el número escrito es 23, los pasos son los siguientes (si hay números pares en el rango de adivinanzas y dos números del medio, elija el más pequeño)

Puedes adivinarlo 7 veces. Este ejemplo usa el pensamiento dicotómico. De acuerdo con este pensamiento, incluso si adivinas el número del 0 al 999, puedes adivinarlo correctamente solo 10 veces como máximo.

Este es un ejemplo de la vida real, ahora volvemos al escenario de desarrollo real. Suponga que hay 1,000 piezas de datos de pedidos, que se han ordenado de acuerdo con el monto del pedido de menor a mayor. El monto de cada pedido es diferente y la unidad más pequeña es el yuan. Ahora queremos saber si hay un pedido con una cantidad igual a $19. Devuelve los datos del pedido si existe, o nulo si no existe

La forma más fácil es, por supuesto, comenzar desde el primer pedido y recorrer los 1000 pedidos uno por uno hasta encontrar un pedido con una cantidad igual a 19 yuanes. Pero será más lento buscar de esta manera En el peor de los casos, es posible que tenga que recorrer los 1000 registros antes de poder encontrarlos. ¿Se puede usar la búsqueda binaria para resolverlo más rápido?

Para facilitar la explicación, asumimos que solo hay 10 pedidos y los montos de los pedidos son: 8, 11, 19, 23, 27, 33, 45, 55, 67, 98

Todavía use la idea de la dicotomía, compare el tamaño con los datos intermedios del intervalo cada vez y reduzca el alcance del intervalo de búsqueda. Como se muestra en la figura a continuación, low y high representan el subíndice del rango que se buscará, y mid representa el subíndice del elemento medio del rango que se buscará.

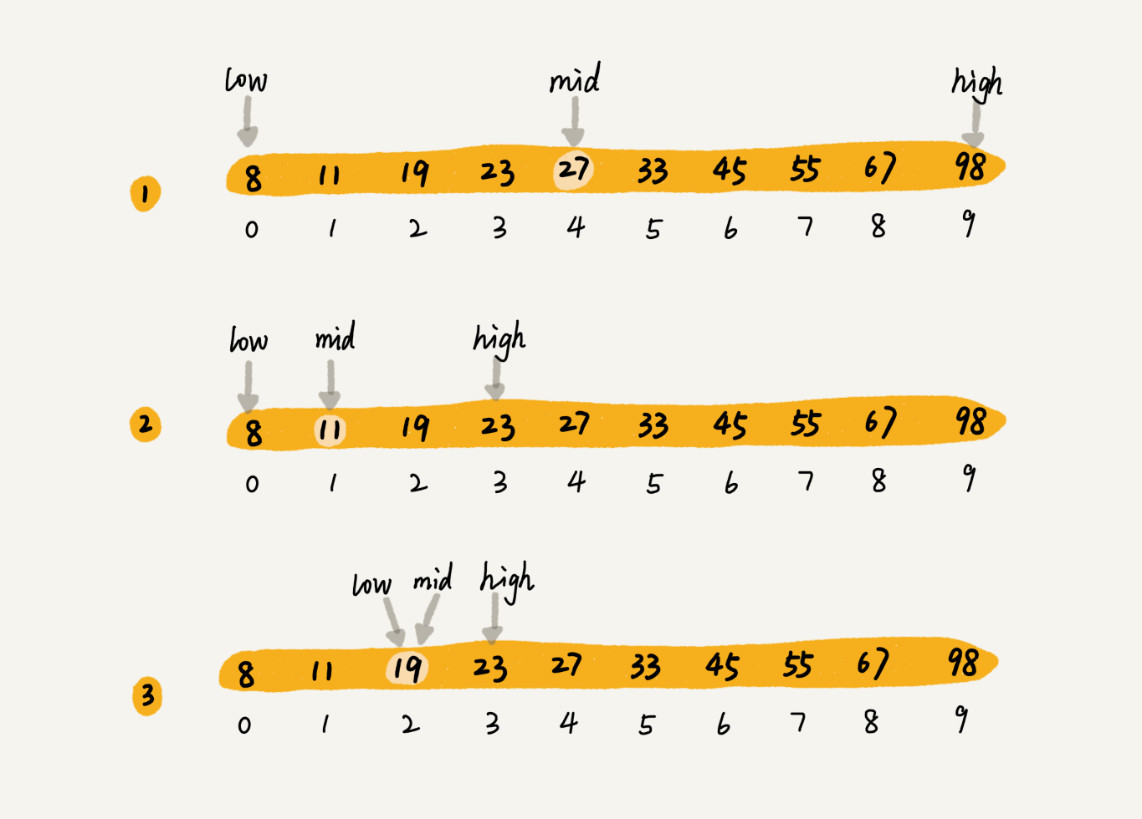
La búsqueda binaria está dirigida a un conjunto de datos ordenados, y la idea de búsqueda es algo similar a la idea de divide y vencerás. Cada vez, comparando con el elemento medio del intervalo, el intervalo a buscar se reduce a la mitad del anterior, hasta que se encuentra el elemento a buscar, o el intervalo se reduce a 0

10.2 O (logn) increíble velocidad de búsqueda

La búsqueda binaria es un algoritmo de búsqueda muy eficiente, ¿qué tan eficiente es? Analicemos su complejidad temporal

Suponemos que el tamaño de los datos es n, y los datos se reducirán a la mitad del tamaño original después de cada búsqueda, es decir, se dividirán por 2. En el peor de los casos, no te detengas hasta que el rango de búsqueda se reduzca a vacío

Se puede ver que se trata de una sucesión geométrica. donde $n/2^{Cuando\; k}$ = 1, el valor de k es el número total de reducciones. Y cada operación de reducción solo implica la comparación del tamaño de dos datos, por lo que después de k veces de operaciones de reducción de intervalos, la complejidad del tiempo es O(k). por$n/2^k$ = 1, podemos obtener k=$registro\_{\_}_{}n$ , entonces la complejidad del tiempo es O(logn)

O(logn) Esta complejidad de tiempo logarítmico . Esta es una complejidad de tiempo extremadamente eficiente, a veces incluso más eficiente que un algoritmo cuya complejidad de tiempo es constante O(1). ¿Por qué dices eso?

Debido a que logn es un orden de magnitud muy "terrible", incluso si n es muy, muy grande, el logn correspondiente también es muy pequeño. Por ejemplo, n es igual a 2 elevado a 32, y este número es aproximadamente 4200 millones. En otras palabras, si usamos la búsqueda binaria de datos en 4200 millones de datos, necesitamos comparar hasta 32 veces

Como dijimos anteriormente, cuando se usa la notación O grande para expresar la complejidad del tiempo, se omiten las constantes, los coeficientes y los órdenes bajos. Para algoritmos con complejidad de tiempo constante, O(1) puede representar un valor constante muy grande, como O(1000), O(10000). Por lo tanto, los algoritmos con complejidad de tiempo constante a veces pueden no ser tan eficientes como los algoritmos O (logn)

Por el contrario, los logaritmos corresponden a exponentes. Hay una muy famosa “La historia de Arquímedes y el rey jugando al ajedrez”, por eso decimos que los algoritmos con complejidad temporal exponencial son ineficaces ante datos a gran escala.

10.3 Implementación recursiva y no recursiva de la búsqueda binaria

De hecho, la búsqueda binaria simple no es difícil de escribir. El caso más simple es que no hay elementos repetidos en la matriz ordenada , y usamos la búsqueda binaria para datos cuyo valor es igual a un valor dado. El código es el siguiente:

public int bsearch(int[] a, int n, int value) {
    
    
  int low = 0;
  int high = n - 1;
 
  while (low <= high) {
    
    
    int mid = (low + high) / 2;
    if (a[mid] == value) {
    
    
      return mid;
    } else if (a[mid] < value) {
    
    
      low = mid + 1;
    } else {
    
    
      high = mid - 1;
    }
  }
 
  return -1;
}

low, high y mid se refieren al subíndice del grupo, donde low y high representan el rango de la búsqueda actual, y low=0 inicial, high=n-1. medio significa la posición media de [bajo, alto]. Al comparar el tamaño de a[mid] y el valor, actualizamos el intervalo que se buscará a continuación hasta que lo encontremos o el intervalo se reduzca a 0, luego salimos

Aquí hay 3 lugares donde es fácil equivocarse

1. Condición de salida del bucle

Tenga en cuenta que bajo<=alto, no bajo<alto

2. El valor de mid

De hecho, mid=(low+high)/2 es problemático. Porque si alto y bajo son relativamente grandes, la suma de los dos puede desbordarse. El método mejorado es escribir el método de cálculo de mid como low+(high-low)/2. Además, si queremos optimizar al máximo el rendimiento, podemos convertir la operación de división por 2 en una operación de bit bajo+((alto-bajo)>>1). Porque las computadoras pueden manejar operaciones de bits mucho más rápido que la división

3. Actualización de baja y alta

bajo=medio+1, alto=medio-1. Preste atención a los +1 y -1 aquí. Si escribe directamente bajo = medio o alto = medio, puede ocurrir un bucle infinito. Por ejemplo, cuando alto = 3, bajo = 3, si a[3] no es igual al valor, hará que el bucle nunca salga

De hecho, además de usar bucles para implementar la búsqueda binaria, también se puede implementar usando recursión , y el proceso es muy simple.

// 二分查找的递归实现
public int bsearch(int[] a, int n, int val) {
    
    
  return bsearchInternally(a, 0, n - 1, val);
}
 
private int bsearchInternally(int[] a, int low, int high, int value) {
    
    
  if (low > high) return -1;
 
  int mid =  low + ((high - low) >> 1);
  if (a[mid] == value) {
    
    
    return mid;
  } else if (a[mid] < value) {
    
    
    return bsearchInternally(a, mid+1, high, value);
  } else {
    
    
    return bsearchInternally(a, low, mid-1, value);
  }
}

10.4 Limitaciones de los escenarios de aplicaciones de búsqueda binaria

1. En primer lugar, la búsqueda binaria se basa en la estructura de la tabla de secuencias, que es simplemente una matriz

¿Puede la búsqueda binaria basarse en otras estructuras de datos? Por ejemplo, lista enlazada. La respuesta es no, la razón principal es que el algoritmo de búsqueda binaria necesita acceder aleatoriamente a los elementos según el subíndice. La complejidad temporal del acceso aleatorio a los datos según el subíndice de la matriz es O(1), mientras que la complejidad temporal del acceso aleatorio de la lista enlazada es O(n). Por lo tanto, si los datos se almacenan en una lista enlazada, la complejidad temporal de la búsqueda binaria será muy alta.

La búsqueda binaria solo se puede utilizar en estructuras de datos donde los datos se almacenan en tablas secuenciales. La búsqueda binaria no se puede aplicar si sus datos se almacenan a través de otras estructuras de datos

2. La búsqueda binaria es para datos ordenados

La búsqueda binaria tiene requisitos estrictos en este punto, y los datos deben estar en orden. Si los datos no están ordenados, primero debemos ordenarlos. Como mencionamos en el capítulo anterior, la menor complejidad temporal de clasificación es O(nlogn). Por lo tanto, si nos dirigimos a un conjunto de datos estáticos sin inserción y eliminación frecuentes, podemos realizar una ordenación y múltiples búsquedas binarias. De esta manera, el costo de clasificación puede amortizarse y el costo marginal de la búsqueda binaria será relativamente bajo.

Sin embargo, si nuestro conjunto de datos tiene operaciones frecuentes de inserción y eliminación, si queremos utilizar la búsqueda binaria, debemos asegurarnos de que los datos aún estén en orden después de cada operación de inserción y eliminación, o ordenarlos antes de cada búsqueda binaria. Para este tipo de recopilación dinámica de datos, sin importar el método, el costo de mantener el orden es muy alto.

Por lo tanto, la búsqueda binaria solo se puede usar en escenarios donde las operaciones de inserción y eliminación son poco frecuentes y una ordenación se realiza varias veces. Para conjuntos de datos que cambian dinámicamente, la búsqueda binaria ya no es aplicable

3. La cantidad de datos es demasiado pequeña para ser adecuada para la búsqueda binaria

Si la cantidad de datos a procesar es pequeña, no hay necesidad de utilizar la búsqueda binaria y el recorrido secuencial es suficiente. Por ejemplo, si buscamos un elemento en una matriz con un tamaño de 10, la velocidad de búsqueda es similar sin importar si usamos búsqueda binaria o recorrido secuencial. Solo cuando la cantidad de datos sea relativamente grande, las ventajas de la búsqueda binaria serán más obvias.

Sin embargo, hay una excepción aquí. Si la operación de comparación entre datos lleva mucho tiempo, independientemente de la cantidad de datos, recomiendo utilizar la búsqueda binaria. Por ejemplo, todas las cadenas con una longitud de más de 300 se almacenan en la matriz, y llevará mucho tiempo comparar el tamaño de dos cadenas tan largas. Necesitamos reducir el número de comparaciones tanto como sea posible, y la reducción del número de comparaciones mejorará en gran medida el rendimiento. En este momento, la búsqueda binaria es más ventajosa que el recorrido secuencial.

4. Demasiados datos no son adecuados para la búsqueda binaria

二分查找的底层需要依赖数组这种数据结构，而数组为了支持随机访问的特性，要求内存空间连续，对内存的要求比较苛刻。比如，我们有 1GB 大小的数据，如果希望用数组来存储，那就需要 1GB 的连续内存空间

注意这里的“连续”二字，也就是说，即便有 2GB 的内存空间剩余，但是如果这剩余的 2GB 内存空间都是零散的，没有连续的 1GB 大小的内存空间，那照样无法申请一个 1GB 大小的数组。而我们的二分查找是作用在数组这种数据结构之上的，所以太大的数据用数组存储就比较吃力了，也就不能用二分查找了

如何在 1000 万个整数中快速查找某个整数？

我们的内存限制是 100MB，每个数据大小是 8 字节，最简单的办法就是将数据存储在数组中，内存占用差不多是 80MB，符合内存的限制。我们可以先对这 1000 万数据从小到大排序，然后再利用二分查找算法，就可以快速地查找想要的数据了

10.5 二分变体

唐纳德·克努特（Donald E.Knuth）在《计算机程序设计艺术》的第 3 卷《排序和查找》中说到：“尽管第一个二分查找算法于 1946 年出现，然而第一个完全正确的二分查找算法实现直到 1962 年才出现”

“十个二分九个错”。二分查找虽然原理极其简单，但是想要写出没有 Bug 的二分查找并不容易，最简单的二分查找写起来确实不难，但是，二分查找的变形问题就没那么好写了

10.5.1 查找第一个值等于给定值的元素

前面写的二分查找是最简单的一种，即有序数据集合中不存在重复的数据，我们在其中查找值等于某个给定值的数据。如果我们将这个问题稍微修改下，有序数据集合中存在重复的数据，我们希望找到第一个值等于给定值的数据，这样之前的二分查找代码还能继续工作吗？

比如下面这样一个有序数组，其中，a[5]，a[6]，a[7] 的值都等于 8，是重复的数据。我们希望查找第一个等于 8 的数据，也就是下标是 5 的元素

Si usamos el código de búsqueda binaria anterior para implementar, primero compare 8 con el valor medio a[4] del intervalo, 8 es mayor que 6, y luego continúe buscando entre los subíndices 5 a 9. La posición media entre los subíndices 5 y 9 es el subíndice 7, a[7] es exactamente igual a 8, por lo que el código devuelve

Aunque a[7] también es igual a 8, no es el primer elemento igual a 8 el que queremos encontrar, porque el primer elemento cuyo valor es igual a 8 es el elemento cuyo índice es 5 en la matriz. Por lo tanto, para este problema de deformación, podemos modificar ligeramente el código.

Si 100 personas escriben búsqueda binaria, habrá 100 formas de escribirla. Hay muchos métodos de implementación de búsqueda binaria deformada en Internet, y muchos de ellos están escritos de manera muy concisa, como el siguiente método de escritura. Sin embargo, aunque es conciso, cuesta mucho entenderlo y es fácil escribir mal.

public int bsearch(int[] a, int n, int value) {
    
    
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    
    
    int mid = low + ((high - low) >> 1);
    if (a[mid] >= value) {
    
    
      high = mid - 1;
    } else {
    
    
      low = mid + 1;
    }
  }
 
  if (low < n && a[low]==value) return low;
  else return -1;
}

Una forma más comprensible de escribir es la siguiente:

public int bsearch(int[] a, int n, int value) {
    
    
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    
    
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
    
    
      high = mid - 1;
    } else if (a[mid] < value) {
    
    
      low = mid + 1;
    } else {
    
    
      if ((mid == 0) || (a[mid - 1] != value)) return mid;
      else high = mid - 1;
    }
  }
  return -1;
}

La relación entre a[mid] y el valor a encontrar tiene tres situaciones: mayor que, menor que o igual a. Para el caso de un valor [mid]>, necesitamos actualizar high= mid-1; para el caso de un valor [mid]<, necesitamos actualizar low=mid+1. Ambos puntos son fáciles de entender. Entonces, ¿qué se debe hacer cuando a[mid]=value?

Si buscamos cualquier elemento cuyo valor sea igual a un valor dado, cuando a[mid] es igual al valor que buscamos, a[mid] es el elemento que buscamos. Sin embargo, si estamos resolviendo para el primer elemento cuyo valor es igual a un valor dado, cuando a[mid] es igual al valor a encontrar, necesitamos confirmar si este a[mid] es el primer elemento cuyo valor es igual a un valor dado

Concéntrese en la línea 11 del código. Si mid es igual a 0, entonces este elemento ya es el primer elemento del arreglo, entonces debe ser lo que buscamos; si mid no es igual a 0, pero el elemento anterior a[mid-1] de a[mid] no es igual a value, también significa que a[mid] es el primer elemento que buscamos cuyo valor es igual al valor dado

Si después de verificar, se encuentra que un elemento a[mid-1] delante de a[mid] también es igual a value, significa que a[mid] en este momento definitivamente no es el primer elemento cuyo valor es igual al valor dado que estamos buscando. Luego actualizamos high=mid-1, porque el elemento que buscamos debe aparecer entre [low, mid-1]

10.5.2 Encontrar el último elemento cuyo valor es igual a un valor dado

El problema anterior es encontrar el primer elemento cuyo valor sea igual al valor dado, ahora cambio un poco la pregunta para encontrar el último elemento cuyo valor sea igual al valor dado, ¿cómo hacerlo?

Simplemente cambie la condición del código anterior a

public int bsearch(int[] a, int n, int value) {
    
    
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    
    
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
    
    
      high = mid - 1;
    } else if (a[mid] < value) {
    
    
      low = mid + 1;
    } else {
    
    
      if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

El foco está en la línea 11 del código. Si el elemento a[mid] ya es el último elemento de la matriz, entonces debe ser lo que buscamos; si el siguiente elemento a[mid+1] de a[mid] no es igual a value, también significa que a[mid] es el último elemento que buscamos cuyo valor es igual al valor dado

Si verificamos y encontramos que un elemento a[mid+1] después de a[mid] también es igual al valor, significa que el a[mid] actual no es el último elemento cuyo valor es igual al valor dado. Actualizaremos low=mid+1, porque el elemento que buscamos debe aparecer entre [mid+1, high]

10.5.3 Encuentra el primer elemento mayor o igual a un valor dado

En una matriz ordenada, encuentra el primer elemento mayor o igual que un valor dado. Por ejemplo, tal secuencia almacenada en la matriz: 3, 4, 6, 7, 10. Si buscas el primer elemento mayor o igual a 5, será 6

De hecho, la idea de implementación es similar a las ideas de implementación de los dos problemas de deformación anteriores, y el código es aún más simple de escribir.

public int bsearch(int[] a, int n, int value) {
    
    
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    
    
    int mid =  low + ((high - low) >> 1);
    if (a[mid] >= value) {
    
    
      if ((mid == 0) || (a[mid - 1] < value)) return mid;
      else high = mid - 1;
    } else {
    
    
      low = mid + 1;
    }
  }
  return -1;
}

Si a[mid] es menor que el valor a buscar, el valor a buscar debe estar entre [mid+1, high], por lo que actualizamos low=mid+1

Para el caso en que a[mid] sea mayor o igual que el valor dado, debemos verificar si este a[mid] es el primer elemento cuyo valor es mayor o igual que el valor dado que estamos buscando. Si no hay ningún elemento antes de a[mid], o el elemento anterior es más pequeño que el valor a encontrar, entonces a[mid] es el elemento que estamos buscando. El código correspondiente a esta lógica es la línea 7

Si a[mid-1] también es mayor o igual que el valor del valor a buscar, significa que el elemento a buscar está entre [low, mid-1], por lo que actualizamos high to mid-1

10.5.4 Encontrar el último elemento menor o igual a un valor dado

Encuentra el último elemento menor o igual a un valor dado. Por ejemplo, dicho conjunto de datos se almacena en la matriz: 3, 5, 6, 8, 9, 10. El último elemento menor o igual a 7 es 6. similar al anterior

public int bsearch7(int[] a, int n, int value) {
    
    
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    
    
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
    
    
      high = mid - 1;
    } else {
    
    
      if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

¿Cómo localizar rápidamente la atribución de una dirección IP?

Si la relación correspondiente entre el rango de IP y la atribución no se actualiza con frecuencia, podemos preprocesar los 120 000 datos y clasificarlos según la IP inicial de menor a mayor. ¿Cómo ordenarlo? Sabemos que una dirección IP se puede convertir en un número entero de 32 bits. Por lo tanto, podemos ordenar las direcciones iniciales de menor a mayor según la relación de tamaño de los valores enteros correspondientes

Entonces, este problema se puede transformar en el problema de cuarta variante "en una matriz ordenada, encuentre el último elemento menor o igual a un valor dado"

Cuando queremos consultar la ubicación de una IP, primero podemos encontrar el último rango de IP cuya IP inicial es menor o igual a esta IP a través de una búsqueda binaria, y luego verificar si la IP está en este rango de IP, si es así, sacaremos la ubicación correspondiente y la mostraremos;