Operaciones Matriciales
que es una matriz
Una matriz es un conjunto de vectores ordenados, donde la dimensión (número característico) del vector es la fila de la matriz, y el número de vectores es la columna de la matriz .
Por ejemplo, un n × mn \times mnorte×La matriz de m significa que haymmm connnUn vector de características n- dimensionales:
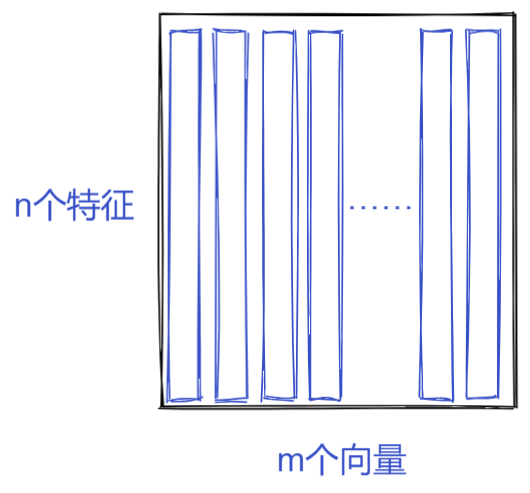
- Este es un 2 × 3 2\times32×La matriz de 3 significa que consta de 3 vectores con 2 características:
x = [ a 11 a 12 a 13 a 21 a 22 a 23 ] x=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_ {23} \end{bmatriz}X=[a11a21a12a22a13a23]
Comprender operaciones con matrices y vectores.
Primero, veamos la operación de una matriz cuadrada y un vector:
w = METRO × v = [ metro 11 metro 12 metro 21 metro 22 ] × [ v 1 v 2 ] = [ v 1 metro 11 + v 2 metro 12 v 2 metro 21 + v 2 metro 22 ] w=M\times v =\begin{bmatrix} m_{11} & m_{12}\\ m_{21} & m_{22}\\ \end{bmatrix} \times \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatriz} v_1 m_{11}+ v_2m_{12}\\ v_2m_{21}+ v_2 m_{22}\end{bmatriz}w=METRO×v=[metro11metro21metro12metro22]×[v1v2]=[v1metro11+v2metro12v2metro21+v2metro22]
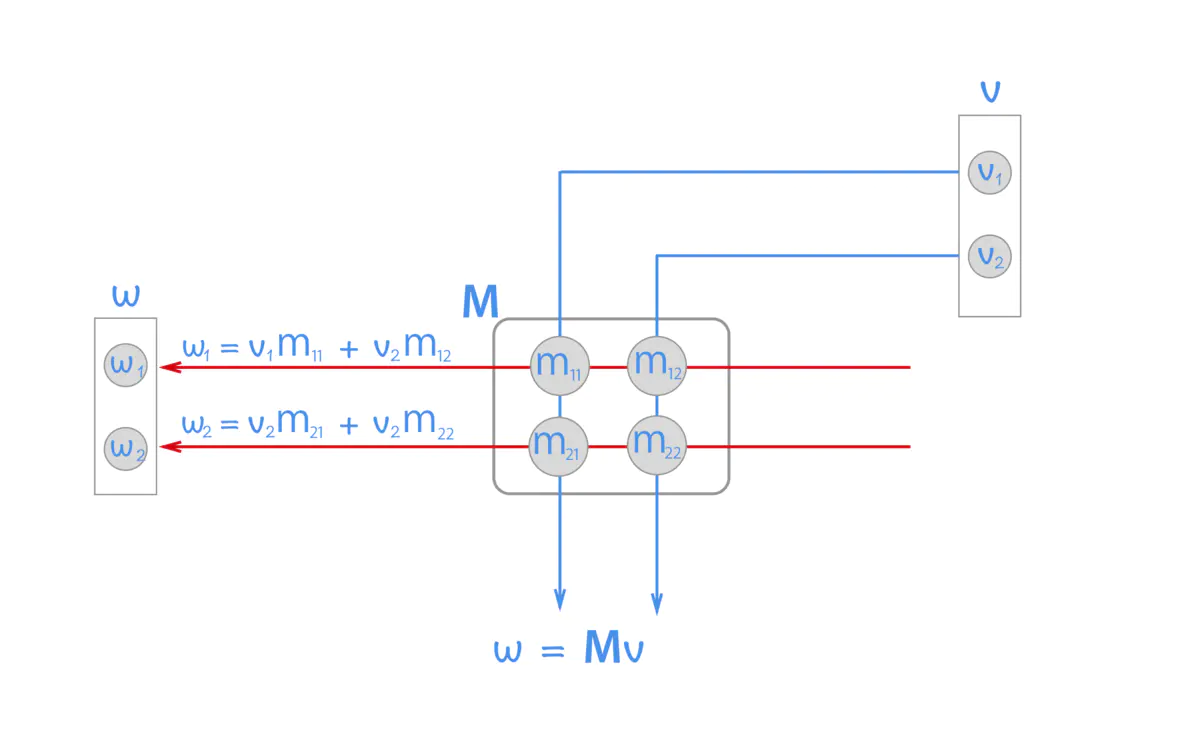
Intuitivamente, primero puedes poner el vector vvv vuelca a la izquierda, luego suma la matriz MMuna vezLos elementos correspondientes de cada fila en M se multiplican y se suman para producir un nuevo resultado cada vez que se procesa un nivel hacia abajo. Por lo tanto, el resultado final de la multiplicación sigue siendo un vector. El número propio de este vector es igual a la matrizMMEl número de filas (características) de M , el número de vectores es igual al vectorvvel número de v .
¿Por qué multiplicar vectores y matrices? Decir la respuesta directamente es transformar el espacio donde se encuentra el vector.
La esencia de las operaciones matriciales: transformación del espacio vectorial (transformación lineal)
En un plano bidimensional, generalmente usamos por defecto su vector base ex = ( 1 , 0 ) , ey = ( 0 , 1 ) e_x=(1,0),e_y=(0,1)mix=( 1 ,0 ) ,mitu=( 0 ,1 ) , por ejemplo, elegimos uno de los vectoresw = 5 ex + 2 eyw=5e_x+2e_yw=5e _x+2e _tu。
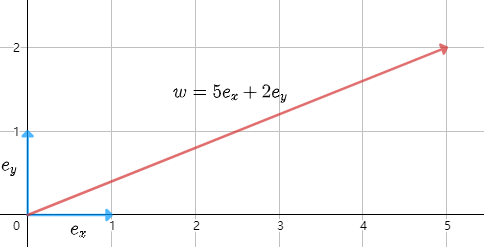
Ahora, necesitamos cambiar un conjunto de vectores base para representar este espacio bidimensional.Durante el proceso de reemplazo, debemos mantener algunas condiciones sin cambios:
- La posición de origen permanece sin cambios;
- Las líneas paralelas siguen siendo líneas paralelas después de la transformación;
- Una línea recta sigue siendo una línea recta después de la transformación;
Las condiciones de transformación anteriores son transformaciones lineales. Se puede imaginar como una distorsión geométrica de las coordenadas espaciales.
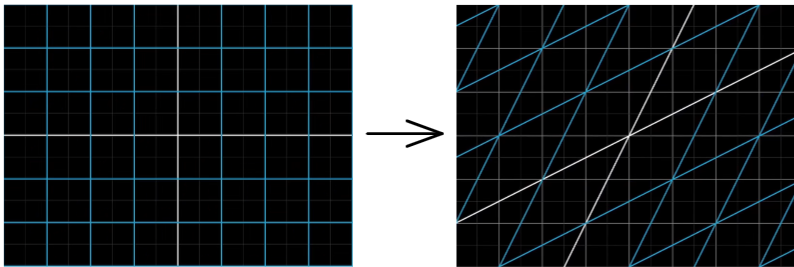
Los vectores en cualquier espacio se pueden obtener mediante operaciones con vectores base, como un vector v = − 1 ex + 2 eyv=-1e_x+2e_yv=- 1 mix+2e _tu。
Después de transformar el espacio, v = − 1 e ^ x + 2 e ^ yv=-1{\hat e}_x+2{\hat e}_yv=− 1mi^x+2mi^tu。
ex = ( 1 , 0 ) , ey = ( 0 , 1 ) e_x=(1,0),e_y=(0,1)mix=( 1 ,0 ) ,mitu=( 0 ,1 )
mi ^ x = ( 1 , − 2 ) , mi ^ y = ( 3 , 0 ) {\ sombrero e}_x=(1,-2),{\ sombrero e}_y=(3,0)mi^x=( 1 ,− 2 ) ,mi^tu=( 3 ,0 )
v ^ = − 1 mi ^ x + 2 mi ^ y = − 1 ( 1 , − 2 ) + 2 ( 3 , 0 ) = ( 5 , 2 ) {\hat v}=-1{\hat e}_x+ 2{\sombrero}_y=-1(1,-2)+2(3,0)=(5,2)v^=− 1mi^x+2mi^tu=− 1 ( 1 ,− 2 )+2 ( 3 ,0 )=( 5 ,2 )
Ahora representamos los vectores como matrices verticales:
v = − 1 [ 1 0 ] + 2 [ 0 1 ] = [ − 1 2 ] v = -1\begin{bmatriz} 1\\0\end{bmatriz} +2\begin{bmatriz} 0\\1\ final{bmatriz} =\comienzo{bmatriz} -1\\2\final{bmatriz}v=− 1[10]+2[01]=[− 12]
v ^ = − 1 [ 1 − 2 ] + 2 [ 3 0 ] = [ 5 2 ] {\ hat v} = -1\begin{bmatrix} 1\\-2\end{bmatrix} +2\begin{bmatrix } 3\\0\end{bmatriz} =\begin{bmatriz} 5\\2\end{bmatriz}v^=− 1[1− 2]+2[30]=[52]
Generalmente, representamos los vectores base transformados como una matriz:
[ 3 2 − 2 1 ] \begin{bmatrix} 3 & 2\\-2 & 1\end{bmatrix}[3− 221]
Más generalmente, denotamos por letras:
[abcd] \begin{bmatrix} a & b\\c & d\end{bmatrix}[adobre]
Ponemos la primera columna [ ac ] \begin{bmatrix} a \\c\end{bmatrix}[ado] como punto de apoyo del primer vector de referencia, la segunda columna[ bb ] \begin{bmatrix} b \\b\end{bmatrix}[bsegundo] como punto de apoyo del segundo vector de referencia. Si esta transformación se aplica al vector[ xy ] \begin{bmatrix} x \\y\end{bmatrix}[Xtu],就会得到[ hacha + bycx + dy ] \left[\begin{array}{l}a x+by \\c x+dy\end{array}\right][una x+por _c x+dy _]。
Además, lo definimos como multiplicación de matrices:
[ abcd ] [ xy ] = x [ ac ] + y [ bd ] = [ ax + bycx + dy ] {\color{Red}\left[\begin{array}{ll}a & b \\c & d\ end{matriz}\right]\left[\begin{matriz}{l}x \\y\end{matriz}\right]=x\left[\begin{matriz}{l}a \\c\end{ matriz}\right]+y\left[\begin{array}{l}b \\d\end{array}\right]=\left[\begin{array}{l}a x+by \\c x +dy\end{matriz}\right]}[adobre][Xtu]=X[ado]+y[bre]=[una x+por _c x+dy _]
multiplicación de matrices
Lo que dijimos anteriormente es usar una matriz para representar una transformación lineal de un vector en un espacio bidimensional, si queremos realizar transformaciones múltiples, es decir, transformaciones compuestas, ¿qué debemos hacer?
Primero debemos realizar una transformación, obtener el vector transformado y realizar la misma transformación. Pero el resultado final debe ser el mismo que el resultado de la transformación de la matriz compuesta al vector.

También podríamos llamar a esto el producto de dos matrices .
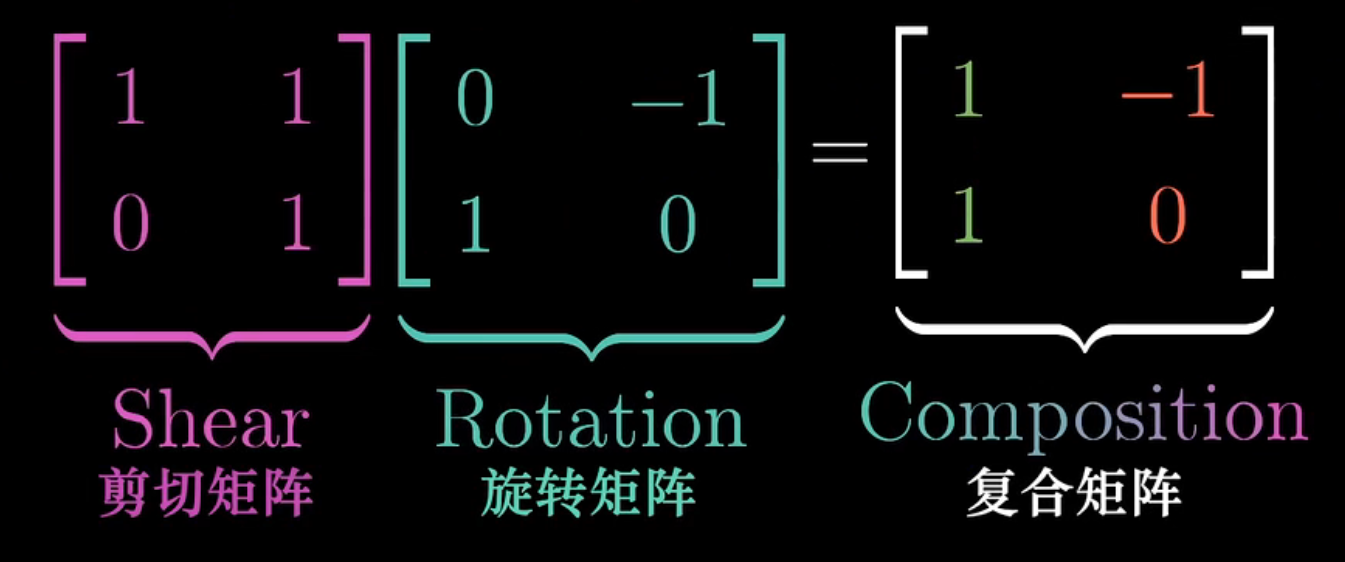
¿Como entender? Puede entenderse como actuando primero sobre la matriz de la derecha y luego actuando sobre la matriz de la izquierda.
Para una multiplicación de matrices general:
[ abcd ] [ efgh ] \left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{ll}e & f \\g & h\end{matriz}\right][adobre][migFh]
Primero podemos considerar el punto de referencia ex e_xmixPrimero cae en [ eg ] \begin{bmatrix} e \\g\end{bmatrix}[mig] ,[ por ejemplo ] \begin{bmatrix} y \\g\end{bmatrix}[mig] y luego se transforma en:
[abcd] [por ejemplo] = [ae + bgce + dg] \left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{ ll}e \\g\end{matriz}\right]=\left[\begin{matriz}{ll}ae+bg\\ce+dg\end{matriz}\right][adobre][mig]=[una mi+b gce+d g]
mismo punto de referencia ey e_ymituDespués de dos transformaciones:
[ abcd ] [ fh ] = [ af + bhcf + dh ] \left[\begin{array}{ll}a & b \\c & d\end{array}\right]\left[\begin{array}{ ll}f \\h\end{matriz}\right]=\left[\begin{matriz}{ll}af+bh\\cf+dh\end{matriz}\right][adobre][Fh]=[una f+bhcf _+d h]
En última instancia, esta multiplicación de matrices se transforma en:
[ abcd ] [ efgh ] = [ ae + bgaf + bhce + dgcf + dh ] {\color{Red}\left[\begin{array}{ll}a & b \\c & d\end{array}\right ]\left[\begin{array}{ll}e & f \\g & h\end{array}\right]=\left[\begin{array}{ll}a e+bg & a f+bh \ \c e+dg & c f+dh\end{matriz}\right]}[adobre][migFh]=[una mi+b gce+d guna f+bhcf _+d h]