2021最后一天，赶紧学习一手吧。由于 Triplet loss 很重要，而代码不复习又很容易忘，这里记录一下。

代码在这里：https://github.com/VisualComputingInstitute/triplet-reid

论文在这里：[1703.07737] In Defense of the Triplet Loss for Person Re-Identification (arxiv.org)

那咱们开始吧！

一、Triplet loss

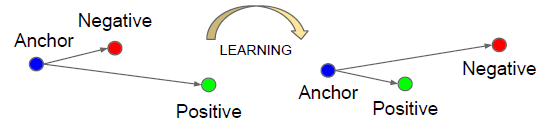
如上图所示，三元组损失(Triplet loss)由anchor、positve、negative组成，简记为<a,p,n>，其中 anchor 表示训练样本，positive 表示预测为整样本，negative表示预测为负样本。

triplet loss的作用：用于减少 positive（正样本）与 anchor 之间的距离，扩大 negative（负样本）与 anchor之间的距离。基于上述三元组，可以构建一个 positive pair <a, p> 和一个 negative pair <a, n>。triplet loss的目的是在一定距离（margin）上把 positive pair 和 negative pair 分开。所以我们希望： $D(a,p)<D(a,n)$ 。进一步希望在一定距离margin上满足这个情况： $D(a,p)+margin<D(a,n)$

其中 $[\cdot]_{+}$ 表示合页函数，也就是待会代码里的 MarginRankingLoss

二、代码实现

搞清楚一个事，Triplet loss 它只是一个loss而已，不会影响样本的训练，所以代码实现是损失怎么写，以及每一行代码代表什么意思。

1. loss.py

def normalize(x, axis=-1):
  
  x = 1. * x / (torch.norm(x, 2, axis, keepdim=True).expand_as(x) + 1e-12)  
  return x


def euclidean_dist(x, y):
 
  m, n = x.size(0), y.size(0) 
  xx = torch.pow(x, 2).sum(1, keepdim=True).expand(m, n) 
  yy = torch.pow(y, 2).sum(1, keepdim=True).expand(n, m).t()
  dist = xx + yy
  dist.addmm_(1, -2, x, y.t())   
  dist = dist.clamp(min=1e-12).sqrt()  
  return dist


def hard_example_mining(dist_mat, labels, return_inds=False):
  
  assert len(dist_mat.size()) == 2 
  assert dist_mat.size(0) == dist_mat.size(1) 
  N = dist_mat.size(0)  
  # shape [N, N]
  is_pos = labels.expand(N, N).eq(labels.expand(N, N).t())  
  is_neg = labels.expand(N, N).ne(labels.expand(N, N).t()) 

  # `dist_ap` means distance(anchor, positive)
  # both `dist_ap` and `relative_p_inds` with shape [N, 1]
  dist_ap, relative_p_inds = torch.max(
    dist_mat[is_pos].contiguous().view(N, -1), 1, keepdim=True)  
  # `dist_an` means distance(anchor, negative)
  # both `dist_an` and `relative_n_inds` with shape [N, 1]
  dist_an, relative_n_inds = torch.min(
    dist_mat[is_neg].contiguous().view(N, -1), 1, keepdim=True)  
  # shape [N]
  dist_ap = dist_ap.squeeze(1)  # compression dimension
  dist_an = dist_an.squeeze(1)

  # calculate the indexs of hard positive and hard negative in dist_mat matrix
  if return_inds:
    # shape [N, N]
    ind = (labels.new().resize_as_(labels)
           .copy_(torch.arange(0, N).long())
           .unsqueeze( 0).expand(N, N))
    # shape [N, 1]
    p_inds = torch.gather(
      ind[is_pos].contiguous().view(N, -1), 1, relative_p_inds.data)
    n_inds = torch.gather(
      ind[is_neg].contiguous().view(N, -1), 1, relative_n_inds.data)
    # shape [N]
    p_inds = p_inds.squeeze(1)
    n_inds = n_inds.squeeze(1)
    return dist_ap, dist_an, p_inds, n_inds

  return dist_ap, dist_an


def global_loss(tri_loss, global_feat, labels, normalize_feature=True):
 
  if normalize_feature:
    global_feat = normalize(global_feat, axis=-1)
  # shape [N, N]
  dist_mat = euclidean_dist(global_feat, global_feat)
  dist_ap, dist_an, p_inds, n_inds = hard_example_mining(
    dist_mat, labels, return_inds=True)
  loss = tri_loss(dist_ap, dist_an)
  return loss, p_inds, n_inds, dist_ap, dist_an, dist_mat

这个代码要怎么看呢？从debug跳转的地方，即 def global_loss(tri_loss, global_feat, labels, normalize_feature=True): 着手

  if normalize_feature:
    global_feat = normalize(global_feat, axis=-1)

这里debug是直接跳过，代表不执行。接着下一步dist_mat = euclidean_dist(global_feat, global_feat)，这显然是在计算global_feat与global_feat之间的欧式距离，那么函数会跳转到euclidean_dist(x,y)，显然这里的x,y都是指global_feat

def euclidean_dist(x, y):
  """
  Args:
    x: pytorch Variable, with shape [m, d]
    y: pytorch Variable, with shape [n, d]
  Returns:
    dist: pytorch Variable, with shape [m, n]
  """

  m, n = x.size(0), y.size(0)  
  xx = torch.pow(x, 2).sum(1, keepdim=True).expand(m, n) 
  yy = torch.pow(y, 2).sum(1, keepdim=True).expand(n, m).t()
  dist = xx + yy
  dist.addmm_(1, -2, x, y.t())   
  dist = dist.clamp(min=1e-12).sqrt()  
  return dist

我们来看一下euclidean_dist(global_feat, global_feat)是怎么计算的。假设global_feat的样本维度为n，则第i个样本为： $\left[a_{i 1}, a_{i 2}, \cdots, a_{i n}\right]$

样本矩阵为：

$\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & \ddots & & a_{2 n} \\ \vdots & & \ddots & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m n} \end{array}\right]_{m \times n}$

xx = torch.pow(x, 2).sum(1, keepdim=True).expand(m, n)

这行代码表示，首先进行pow(x,2)，即元素级幂运算，样本矩阵变为：

$\left[\begin{array}{cccc} a_{11}^{2} & a_{12}^{2} & \cdots & a_{1 n}^{2} \\ a_{21}^{2} & \ddots & & a_{2 n}^{2} \\ \vdots & & \ddots & \vdots \\ a_{m 1}^{2} & a_{m 2}^{2} & \cdots & a_{m n}^{2} \end{array}\right]_{m \times n}$

然后对每行元素进行求和，同时保持维度，sum(dim=1.keepdim=True)；紧接着在将其扩张为 m x n 阶矩阵（在代码里m=n=128)：

$\left[\begin{array}{cc} \sum_{k=1}^{n} & a_{1 k}^{2} \\ \sum_{k=1}^{n} & a_{2 k}^{2} \\ \vdots & \\ \sum_{k=1}^{n} & a_{m k}^{2} \end{array}\right]_{m \times 1}\rightarrow \left[\begin{array}{cccc} \sum_{k=1}^{n} a_{1 k}^{2} & \sum_{k=1}^{n} a_{1 k}^{2} & \cdots & \sum_{k=1}^{n} a_{1 k}^{2} \\ \sum_{k=1}^{n} a_{2 k}^{2} & \ddots & & \sum_{k=1}^{n} a_{2 k}^{2} \\ \vdots & & \ddots & \vdots \\ \sum_{k=1}^{n} a_{m k}^{2} & \sum_{k=1}^{n} a_{m k}^{2} & \cdots & \sum_{k=1}^{n} a_{m k}^{2} \end{array}\right]_{m \times n}$

dist = xx + yy

将其与其转置相加（在代码里m=n=128 ），得到的 dist 矩阵为：

$\left[\begin{array}{cccc} \sum_{k=1}^{n} a_{1 k}^{2} & \sum_{k=1}^{n} a_{1 k}^{2} & \cdots & \sum_{k=1}^{n} a_{1 k}^{2} \\ \sum_{k=1}^{n} a_{2 k}^{2} & \ddots & & \sum_{k=1}^{n} a_{2 k}^{2} \\ \vdots & & \ddots & \vdots \\ \sum_{k=1}^{n} a_{m k}^{2} & \sum_{k=1}^{n} a_{m k}^{2} & \cdots & \sum_{k=1}^{n} a_{m k}^{2} \end{array}\right]_{m \times m}+\left[\begin{array}{cccc} \sum_{k=1}^{n} a_{1 k}^{2} & \sum_{k=1}^{n} a_{2 k}^{2} & \cdots & \sum_{k=1}^{n} a_{m k}^{2} \\ \sum_{k=1}^{n} a_{1 k}^{2} & \ddots & & \sum_{k=1}^{n} a_{m k}^{2} \\ \vdots & & \ddots & \vdots \\ \sum_{k=1}^{n} a_{1 k}^{2} & \sum_{k=1}^{n} a_{2 k}^{2} & \cdots & \sum_{k=1}^{n} a_{m k}^{2} \end{array}\right]_{m \times m}=$

$\left[\begin{array}{cccc} \sum_{k=1}^{n}\left(a_{1 k}^{2}+a_{1 k}^{2}\right) & \sum_{k=1}^{n}\left(a_{1 k}^{2}+a_{2 k}^{2}\right) & \cdots & \sum_{k=1}^{n}\left(a_{1 k}^{2}+a_{m k}^{2}\right) \\ \sum_{k=1}^{n}\left(a_{2 k}^{2}+a_{1 k}^{2}\right) & \ddots & & \sum_{k=1}^{n}\left(a_{2 k}^{2}+a_{m k}^{2}\right) \\ \vdots & & \ddots & \vdots \\ \sum_{k=1}^{n}\left(a_{m k}^{2}+a_{1 k}^{2}\right) & \sum_{k=1}^{n}\left(a_{m k}^{2}+a_{2 k}^{2}\right) & \cdots & \sum_{k=1}^{n}\left(a_{m k}^{2}+a_{m k}^{2}\right) \end{array}\right]_{m \times m}$

dist.addmm_(1, -2, x, y.t())

这一行代码是在执行公式： dist=1*dist-2*(x @ $y^{T}$ ) ，其中@为矩阵乘法

化简得出最后结果为：

$\left[\begin{array}{cccc} \sum_{k=1}^{n}\left(a_{1 k}-a_{1 k}\right)^{2} & \sum_{k=1}^{n}\left(a_{1 k}-a_{2 k}\right)^{2} & \cdots & \sum_{k=1}^{n}\left(a_{1 k}-a_{m k}\right)^{2} \\ \sum_{k=1}^{n}\left(a_{2 k}-a_{1 k}\right)^{2} & \ddots & & \sum_{k=1}^{n}\left(a_{2 k}-a_{m k}\right)^{2} \\ \vdots & & \ddots & \vdots \\ \sum_{k=1}^{n}\left(a_{m k}-a_{1 k}\right)^{2} & \sum_{k=1}^{n}\left(a_{m k}-a_{2 k}\right)^{2} & \cdots & \sum_{k=1}^{n}\left(a_{m k}-a_{m k}\right)^{2} \end{array}\right]_{m \times m}$

可能这样看不出什么神奇，我们来验证一下：假设第i个样本 $s_{i}$ 为 $\left[a_{i 1}, a_{i 2}, \cdots, a_{i n}\right]$ ，第j个样本 $\boldsymbol{s}_{j}$ 为 $\left[a_{j 1}, a_{j 2}, \cdots, a_{j n}\right]$ ，则样本的差值为：

$s_{i}-s_{j}=\left[a_{i 1}-a_{j 1}, a_{i 2}-a_{j 2}, \cdots, a_{i n}-a_{j n}\right]$ ，紧接着，L2范数（也就是欧氏距离）为： $\|x\|_{2}=\left(\left|x_{1}\right|^{2}+\left|x_{2}\right|^{2}+\cdots+\left|x_{n}\right|^{2}\right)^{1 / 2}$

亦即： $\left\|s_{i}-s_{j}\right\|_{2}=\left(\left|a_{i 1}-a_{j 1}\right|^{2}+\left|a_{i 2}-a_{j 2}\right|^{2}+\cdots+\left|a_{i n}-a_{j n}\right|^{2}\right)^{1 / 2}$ ，给它平方一下再整理，容易得到： $\left\|s_{i}-s_{j}\right\|_{2}^{2}=\left(\left|a_{i 1}-a_{j 1}\right|^{2}+\left|a_{i 2}-a_{j 2}\right|^{2}+\cdots+\left|a_{i n}-a_{j n}\right|^{2}\right)=\sum_{k=1}^{n}\left(a_{i k}-a_{j k}\right)^{2}$ 。这表示什么意思？即第i个样本与第j个样本的平方距离。

dist = dist.clamp(min=1e-12).sqrt()

最后，进行区间压缩，最小值设为1e-12,同时进行元素级开方（有出入： $\sum_{i}^{N}\left[\left\|f\left(x_{i}^{a}\right)-f\left(x_{i}^{p}\right)\right\|_{2}^{2}-\left\|f\left(x_{i}^{a}\right)-f\left(x_{i}^{n}\right)\right\|_{2}^{2}+\alpha\right]_{+}$ ）

这一步dist_mat = euclidean_dist(global_feat, global_feat)计算完了，现在得到了一个大小为 128 x 128 的 dist_mat 矩阵，它计算的是global_feat 间的欧氏距离。下一步 debug 到 dist_ap, dist_an, p_inds, n_inds = hard_example_mining(dist_mat, labels, return_inds=True)，跳转到 def hard_example_mining() 模块。

def hard_example_mining(dist_mat, labels, return_inds=False):
  
  assert len(dist_mat.size()) == 2 
  assert dist_mat.size(0) == dist_mat.size(1) 
  N = dist_mat.size(0)  
  # shape [N, N]
  is_pos = labels.expand(N, N).eq(labels.expand(N, N).t())  
  is_neg = labels.expand(N, N).ne(labels.expand(N, N).t()) 

  # `dist_ap` means distance(anchor, positive)
  # both `dist_ap` and `relative_p_inds` with shape [N, 1]
  dist_ap, relative_p_inds = torch.max(
    dist_mat[is_pos].contiguous().view(N, -1), 1, keepdim=True)  
  # `dist_an` means distance(anchor, negative)
  # both `dist_an` and `relative_n_inds` with shape [N, 1]
  dist_an, relative_n_inds = torch.min(
    dist_mat[is_neg].contiguous().view(N, -1), 1, keepdim=True)  
  # shape [N]
  dist_ap = dist_ap.squeeze(1)  # compression dimension
  dist_an = dist_an.squeeze(1)

  if return_inds:
    # shape [N, N]
    ind = (labels.new().resize_as_(labels)
           .copy_(torch.arange(0, N).long())
           .unsqueeze( 0).expand(N, N))
    # shape [N, 1]
    p_inds = torch.gather(
      ind[is_pos].contiguous().view(N, -1), 1, relative_p_inds.data)
    n_inds = torch.gather(
      ind[is_neg].contiguous().view(N, -1), 1, relative_n_inds.data)
    # shape [N]
    p_inds = p_inds.squeeze(1)
    n_inds = n_inds.squeeze(1)
    return dist_ap, dist_an, p_inds, n_inds

  return dist_ap, dist_an

这一块代码主要是在进行样本挖掘，也就是找到hardest positive 和 hardest negative. 在解析之前，我们要先弄清楚hard_example_mining(dis_mat, labels, return_inds=False) 函数的输入输出是什么。

输入：
1.距离矩阵dist_mat，维度(batch_size,batch_size)（(注意啦，在代码里P=32,K=4，而在论文里P=18,K=4））
2.本批次特征向量对应的行人ID labels，维度(batch_size)
3.是否返回最小相似度正样本与最大相似度负样本所对应的距离矩阵的序号return_indexs，默认为False

输出：
1.正样本区（hardest positive)最小相似度张量dist_ap，维度(batch_size)
2.负样本区（hardest negative)最大相似度张量dist_an，维度(batch_size)
3.正样本区最小相似度样本对应的距离矩阵下标p_indexs，维度(batch_size)
4.负样本区最大相似度样本对应的距离矩阵下标,n_indexs，维度(batch_size)

接下来，我们开始学习样本挖掘的写法（注意思路）。

assert len(dist_mat.size()) == 2  #先判断dis_mat是不是二维矩阵，若不是，则报错

assert dist_mat.size(0) == dist_mat.size(1) #再判断dis_mat是否为方阵，若不是，则报错

#挖掘hardest_positive,相同标签为True,不同标签为False
is_pos = labels.expand(N, N).eq(labels.expand(N, N).t())  

#挖掘hardest_negative,相同标签为True,不同标签为False
is_neg = labels.expand(N, N).ne(labels.expand(N, N).t())

#计算最小相似度（最大距离）正样本距离与最小相似度所对应正样本的序号（序号范围0~N-1）
'''
torch.max函数不仅返回每一列中最大值的那个元素，并且返回最大值对应索引
.contiguous()用于将dis_mat中正样本区dist_mat[is_pos]的距离矩阵拉成一维连续向量
.view(N,-1)用于改变矩阵形状，N表示行数，-1表示自动填充列

'''
dist_ap, relative_p_inds = torch.max(
    dist_mat[is_pos].contiguous().view(N, -1), 1, keepdim=True)

#计算最大相似度（最小距离）负样本距离与最大相似度所对应负样本的序号（序号范围0~N-1）
dist_an, relative_n_inds = torch.min(
    dist_mat[is_neg].contiguous().view(N, -1), 1, keepdim=True)

#上面计算得到的dist_ap与dist_an维度(batch_size,1)压缩，最后维度维[batch_size,]
#squzze(1)表示去除size为1的维度
dist_ap = dist_ap.squeeze(1)  # compression dimension
  dist_an = dist_an.squeeze(1)

#计算最小相似度正样本与最大相似度负样本在距离矩阵中的序号
if return_inds:
    # shape [N, N]
    ind = (labels.new().resize_as_(labels)
           .copy_(torch.arange(0, N).long())
           .unsqueeze( 0).expand(N, N))
    # shape [N, 1]
    p_inds = torch.gather(
      ind[is_pos].contiguous().view(N, -1), 1, relative_p_inds.data)
    n_inds = torch.gather(
      ind[is_neg].contiguous().view(N, -1), 1, relative_n_inds.data)
    # shape [N]
    p_inds = p_inds.squeeze(1)
    n_inds = n_inds.squeeze(1)
    return dist_ap, dist_an, p_inds, n_inds

行，现在样本挖掘也处理完了，debug到下一步：loss=tri_loss(dist_ap,dist_an)，这时候代码会跳转到 TripletLoss.py , 我们接着学习损失计算怎么写。

2. TripletLoss.py

class TripletLoss(object):
  def __init__(self, margin=None):
    self.margin = margin
    if margin is not None:
      self.ranking_loss = nn.MarginRankingLoss(margin=margin)
    else:
      self.ranking_loss = nn.SoftMarginLoss()

  def __call__(self, dist_ap, dist_an):
    y = Variable(dist_an.data.new().resize_as_(dist_an.data).fill_(1))
    if self.margin is not None:
      loss = self.ranking_loss(dist_an, dist_ap, y)
    else:
      loss = self.ranking_loss(dist_an - dist_ap, y)
    return loss

代码怎么看？老规矩还是从debug到的地方开始追根溯源。从上面 loss=tri_loss(dist_ap,dist_an) debug下来刚好到 def __call__(self,dist_ap,dist_an)，那我们来看这一段什么意思：

#dist_an.data.new()：构建一个与dist_an相同的Tensor
 .resize_as_(dist_an.data)：设置维度与dist_an相同
 .fill_(1)：填充scale为1，也就是MarginRankingLoss中的y，设置为1（注意，这非常重要）#

def __call__(self, dist_ap, dist_an):
    y = Variable(dist_an.data.new().resize_as_(dist_an.data).fill_(1))

紧接着进入到if循环中，debug到 loss = self.ranking_loss(dist_an, dist_ap, y)计算三元组损失，跳转到class TripletLoss(object): ，我们来看看这一段是怎么实现损失计算的：

class TripletLoss(object):
  def __init__(self, margin=None):
    self.margin = margin
    if margin is not None:
      self.ranking_loss = nn.MarginRankingLoss(margin=margin)
    else:
      self.ranking_loss = nn.SoftMarginLoss()

这里最重要的一步是 self.ranking_loss = nn.MarginRankingLoss(margin=margin)，要弄清代码干了什么，我们先要了解nn.marginRankingLoss(margin)函数

首先TripletMarginLoss() 函数是专门用来计算Triplet Loss的，这里用 nn.MarginRankingLoss() 也是可以计算的，与TripletMarginLoss不同的是，它的输入是不再是三个原始的向量anchor, positive, negative，而是计算好 $d_{ap}$ 和 $d_{an}$ 的值，再输入进去。在nn.MarginRankingLoss() 的公式中： $\operatorname{loss}(x, y)=\max (0,-y *(x 1-x 2)+\operatorname{margin})$ ，如果能让y等于全1向量， $x_{1}=d_{an}$ ， $x_{2}=d_{ap}$ ,那么公式就成为：

这刚好是Triplet Loss 的公式呀

现在回到刚才这一步： loss = self.ranking_loss(dist_an, dist_ap, y) 是不是突然间豁然开朗了，知道为什么说理解y很重要了吧，哎，这就是python的魅力。

三、结尾

至此，三元组损失的核心代码就解读完毕了，当然，我这也是站在巨人的肩膀上总结的而已。趁着2021的最后一天，喝点小酒去了.

参考博客：模块笔记1：TripletLoss - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/402040769 行人重识别(18)——代码实践之难样本挖掘算法（hard_example_mining.py）_R.I.P Kobe Bryant-CSDN博客_样本挖掘算法介绍难样本挖掘算法（hard_example_mining.py）的作用、编写思路、python代码。https://blog.csdn.net/qq_43270828/article/details/112170542

Triplet loss 源码解析

一、Triplet loss

二、代码实现

1. loss.py

2. TripletLoss.py

三、结尾

Supongo que te gusta