Encuentre los bordes críticos y los bordes pseudocríticos en el árbol de expansión mínimo

Darte una nnGráfico conectado no dirigido ponderado con$n$ puntos, el número de nodo es$0$ hasta$norte-1$ , y también hay una matriz de$edges$， 其中$edges\left[i\right]=[Fro{m}_{yo},t{O}_{yo},weigh{t}_{yo}]$表示 在$fro{m}_{yo}$和$t{O}_{yo}$Hay un borde no dirigido ponderado entre los nodos. Árbol de expansión mínimo $\left(MST\right)$ es un subconjunto de bordes en un gráfico dado, que conecta todos los nodos y no tiene bucles, y la suma de los pesos de estos bordes es la más pequeña.

Busque todos los bordes clave y los bordes pseudo clave del árbol de expansión mínimo en un gráfico determinado. Si se elimina un borde del gráfico, dará lugar a un aumento en el peso del árbol de expansión mínimo, entonces decimos que es un borde crítico. Los bordes pseudocríticos son bordes que pueden aparecer en algunos árboles de expansión mínima pero no en todos los árboles de expansión mínima.

Tenga en cuenta que puede devolver los subíndices de los bordes de clave y los bordes de pseudo-clave en cualquier orden, respectivamente.
Ejemplo 1:

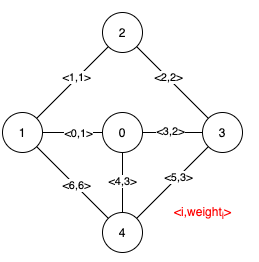
Entrada: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
Salida: [[0,1],[2,3,4,5]]
Explicación: La figura anterior describe la figura dada.
La siguiente figura muestra todos los árboles de expansión mínimos.

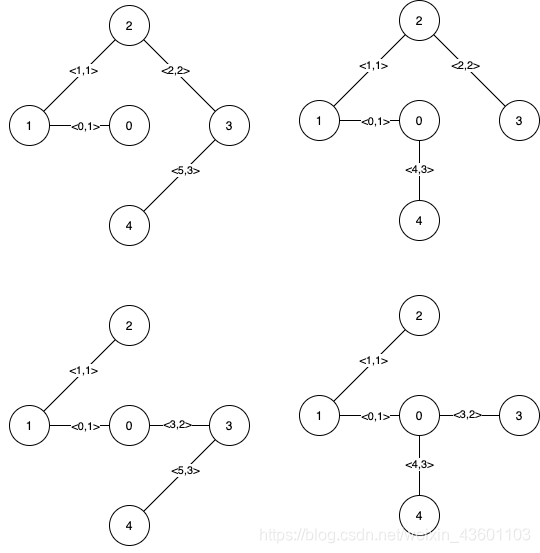
Tenga en cuenta que el borde 0 y el borde 1 aparecen en todos los árboles de expansión mínimos, por lo que son los bordes clave. Usamos estos dos subíndices como la primera lista de salida.
Los bordes 2, 3, 4 y 5 son los bordes restantes de todos los MST, por lo que son bordes pseudocríticos. Los usaremos como la segunda lista de salida.
Ejemplo 2:

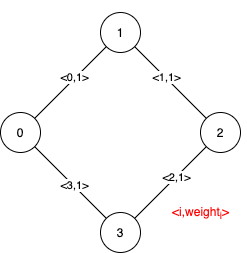
Entrada: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
Salida: [[],[0,1,2,3]]
Explicación: Se puede observar que 4 aristas tienen el mismo peso, y se pueden elegir 3 de ellas para formar un MST. Entonces, los 4 bordes son todos bordes pseudocríticos.
Consejos:
$$\begin{gathered} 2<=norte<=100 \\ 1<=edges.length<=min(200,\frac{n*(n-1)}{2}) \\ edges\left[i\right].length==3 \\ 0<=fro{m}_{yo}<t{O}_{yo}<norte \\ 1<=weigh{t}_{yo}<=1000 \end{gathered}$$
所有$(Fro{m}_{yo},t{O}_{yo})\; Los$ pares de números son diferentes entre sí.

Ideas

Primero necesitamos entender la definición de "borde crítico" y "borde pseudocrítico" en la descripción del título:

• Borde crítico: si se elimina un borde del árbol de expansión mínimo, esto dará lugar a un aumento en el peso del árbol de expansión mínimo, entonces decimos que es un borde crítico. En otras palabras, si el peso del árbol de expansión mínimo de la imagen original se establece en $\text{valor}$ , luego, después de eliminar este borde:

  • O el gráfico completo no está conectado y no hay un árbol de expansión mínimo;
  • O el gráfico completo está conectado y el peso del árbol de expansión mínimo correspondiente es $v$ , que es estrictamente mayor que$\text{valor}$。

• Bordes pseudocríticos: bordes que pueden aparecer en algunos árboles de expansión mínima pero no en todos los árboles de expansión mínima. Es decir, podemos considerar este borde primero en el proceso de calcular el árbol de expansión mínimo, es decir, primero fusionar los dos puntos finales de este borde en el conjunto de consultas de combinación. Sea el peso final mínimo del árbol de expansión $v$ , si$v=\text{valor}$ , entonces este borde es un borde pseudocrítico.

Cabe señalar que los bordes de clave también satisfacen las propiedades correspondientes de los bordes de pseudo-clave. Por lo tanto, primero ejecutamos Kruskal \ texttt {Kruskal} en la imagen originalAlgoritmo de$\text{Kruskal}$ , obtenga el valor de peso del árbol de expansión mínimo$\text{valor}$ , luego enumeramos cada borde, primero juzgamos si es un borde crítico de acuerdo con el método anterior, si no es un borde crítico, luego juzgamos si es un borde pseudocrítico.

#include <bits/stdc++.h>

using namespace std;
const int maxn = 110;
int a[maxn][maxn];

int main() {
    
    
    int n;
    while (~scanf("%d", &n)) {
    
    
        if (!n) break;
        for (int i = 1; i <= n; i++) {
    
    
            int x = i, y = i;
            for (int j = 1; j <= n - i + 1; j++) {
    
    
                a[x][y] = j;
                x++;
            }
            x = i;
            y = i;
            for (int j = 1; j <= n - i + 1; j++) {
    
    
                a[x][y] = j;
                y++;
            }
        }
        for (int i = 1; i <= n; i++) {
    
    
            for (int j = 1; j <= n; j++) {
    
    
                printf("%d", a[i][j]);
                if (j == n) puts(""); else printf(" ");
            }
        }
        puts("");
    }
    return 0;
}