Geometría computacional (1) casco convexo

Geometría computacional (1) casco convexo

Resolver el área de un triángulo : fórmula de Helen-Qin Jiushao

Juzgando que cierto punto está en el lado izquierdo de una cierta línea recta : use la fórmula de Helen anterior

bool ToLeft(Point p, Point q, Point s)
{
    return Area2(p, q, s) > 0;
}

int Area2(Point p, Point q, Point s)
{
    return 
        p.x * q.y - p.y * q.x 
       +q.x * s.y - q.y * s.x
       +s.x * p.y - s.y *p.x;
}

Juzgue si un punto está dentro del triángulo : entonces los tres puntos están conectados en sentido antihorario para formar un borde dirigido. Si el punto está en el lado izquierdo de las tres líneas rectas, entonces es cierto. (La complejidad es O (n ^ 4))

bool InTriangle(Point p, Point q, Point r, Point s)
{
    bool pqLeft = ToLeft(p, q, s);
    bool qrLeft = ToLeft(q, r, s);
    bool rpLeft = ToLeft(r, p, s);
    return (pdLeft == qrLeft) && (qrLeft == rqLeft);
}

Encuentra todos los polos

1. Dibuje una línea recta a lo largo de este punto, y se debe encontrar una línea recta, de modo que todos los demás puntos estén en un lado de la línea para determinar si es un polo (la complejidad es O (n ^ 3))

void markEE(Point S[], int n) //n>2
{
    for(int k = 0; k <n; k ++)
        S[k].extreme = False; //先假设所有的点都不是极点
    for(int p = 0; p < n; p ++)
        for(int q = p + 1; q < n; q ++)
            checkEdge(S, n, p, q);
}

void checkEdge(Point S[], int n, int p, int q)
{
    bool LEmpty = True, REmpty = True;
    for(int k = 0; k < n && (LEmpty || REmpty); k ++)
    {
        if(k != p && k != q)
        {
            ToLeft(S[p], S[q], S[k]) ? LEmpty = False : REmpty = False;
        }
    }
    if(LEmpty || REmpty)
        S[p].extreme = S[q].extreme = True;
}

2. Algoritmo de Jarvis: Aquí, en sentido antihorario se define como la dirección positiva. El predecesor de un punto es el siguiente punto en el sentido antihorario y el sucesor es el siguiente punto en el sentido de las agujas del reloj. El algoritmo de Javis March es sensible a la salida y su complejidad cambiará con la escala del casco convexo.

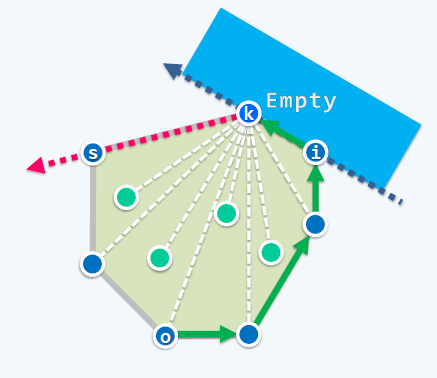
void Jarvis(Point S[], int n)
{
    for(int k = 0; k < n; k ++)
        S[k].extreme = false;  //假设所有的点都不是极点
    int ltl = LTL(S, n); int k = ltl;  //先利用LTL算法找到第一个极点,k是起点
    do
    {
        P[k].extreme = true; int s = -1;  //s是要找的下一个极点，用t去循环找
        for(int t = 0; t < n; t ++)
        {
            if(t != k && t != s && (s == -1 || !ToLeft(P[k], P[s], P[t])) 
                s = t; //如果t在pq的右边，更新s
        }
        P[k].succ = s; k = s; //新的极边pq确定
    }while(ltl != k); //如果循环回到了原点，结束
}

int LTL(Point S[], int n)
{
    int ltl = 0;
    for(int k = 1; k < n; k ++)
    {
        if(P[k].y < P[ltl].y || (P[k].y == P[ltl].y && P[k].x < P[ltl].x)
            ltl = k;
    }
    return ltl;
}

Juzgue si un cierto punto está dentro del polígono : haga un rayo para cualquier punto v del punto x y el casco convexo original, entonces v tiene un predecesor y un sucesor, si el predecesor y el sucesor están a la derecha oa la izquierda del rayo, entonces es una tangente . Si no se encuentra tal tangente, entonces el punto está dentro del casco convexo.

3. Algoritmo de Graham Scan: Primero, hay un borde polar (LTL), y luego los puntos restantes se ordenan de pequeños a grandes según el ángulo polar. Hay una pila S y una pila T. Inicialmente, el punto 1 y el punto 2 están en la pila S, y los otros puntos van desde la parte superior de la pila T hasta la parte inferior de la pila. Código principal: si el punto en la parte superior de la pila T está a la izquierda de los dos puntos en la parte superior y el segundo en la parte superior de la pila S, entonces empuje el punto en la parte superior de la pila T en la pila S, de lo contrario, saque el punto en la parte superior de la pila S. Todos los elementos de la pila S al final del programa son todos polos.

while(!T.empty())
{
    toLeft(S[1],S[0],T[0]) ? S.push(T.pop()) : S.pop();
}

4. Dividir y conquistar (Dividir y conquistar): agrupe adecuadamente varios puntos, construya cascos subconvexos por separado y luego combínelos en un casco convexo

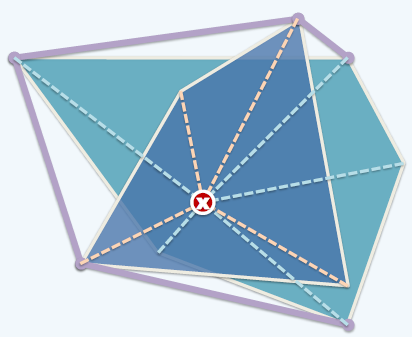
Para la imagen de arriba, es una situación mejor, porque los polos de los dos cascos subconvexos se ordenan por separado del núcleo, entonces solo se necesitan dos formas para convertir estos puntos en un orden general, y luego se realiza Graham Scan.

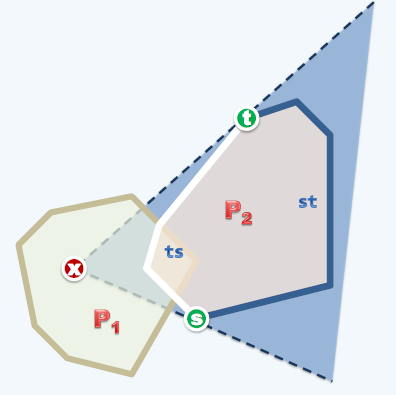
Solo encontramos dos puntos de corte, entonces el segmento ts es inútil. Luego, después de descartar ts, realice una fusión bidireccional en el punto del segmento st y otro casco subconvexo, y luego realice Graham Scan.

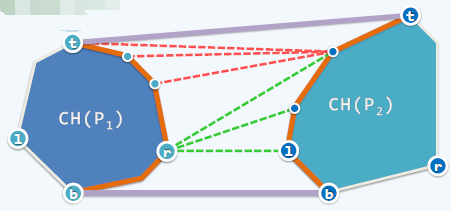
Primero, cuando se construyen los dos cascos subconvexos, pueden estar separados por una línea vertical. Solo necesitamos encontrar dos tangentes para fusionar los dos cascos subconvexos. Nuestra operación real es primero encontrar el punto más a la derecha del casco subconvexo izquierdo, y luego encontrar el punto más a la izquierda del casco subconvexo derecho. El método de búsqueda aquí solo necesita registrar sus puntos más a la izquierda y más a la derecha al construir el casco subconvexo paso a paso, luego solo toma O (1) tiempo para encontrarlo cuando sea necesario, de lo contrario, debe usarse O (n) tiempo para encontrar estos dos puntos.