Suffix automaton emotional understanding

Suffix automaton is actually not well understood, especially the direct proof to see a large section of, do not know what it's doing, it might be a bit ignorant

That let me introduce my good emotional understanding, we look at this article might be a better understanding of other people's blog QAQ

Front cheese: trie tree

Before speaking about the false suffix tree ($ n ^ 2 $), because it is fake so it is easy to understand, do not be afraid

Figure steal .jpg

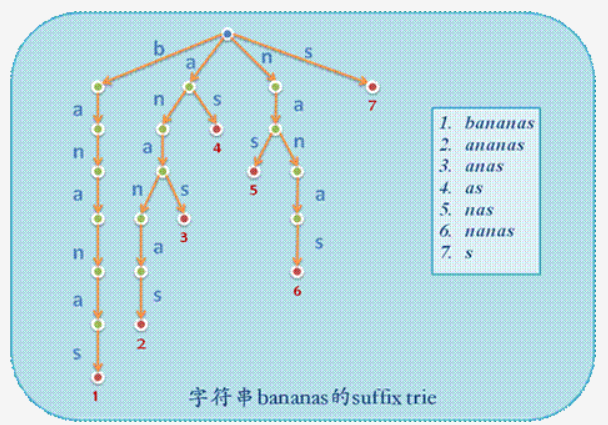
For a string (Example: \ (bananas were \) ), the suffixes of it ($ bananas were, the ananas, Nanas, Anas, NAS, AS, S \ () is inserted into a a trie tree, and at the end marked end mark is the suffix of violence \) Trie \ (a, apparently time and space complexity are \) O (the n-^ 2) $

It can be said suffix automaton it is largely optimized, i.e. sub-string and the suffix for recurring operations such as compression, the complexity of the space-time dip of \ (O (n-) \) , and having Some properties of suffix tree

Substring understanding of: for a substring of the string S, it will be appreciated that as you ((a suffix of S) prefix), no problems

That is, if a path string in the sub-trie S is a constant starting from the root

Dim it

Find a substring occurrences: to find its path in the trie, at the end of its mark and below, that is, it is a prefix number suffix
Find a substring first (last) occurrence position, above, is walked down the maximum depth (depth minimum) marks the end
The number of different sub-strings of statistical nature, i.e., the number of trie node tree

He began to cut into the suffix automaton:

Suffix automaton magic even a lot of edge, successfully reduced the space and time

He had a little nature: starting from the start node, and take any path, the path termination nodes are the original string is a suffix, may be more than a termination node

First posted a picture, blog from zjp chiefs to facilitate the understanding of the nature:

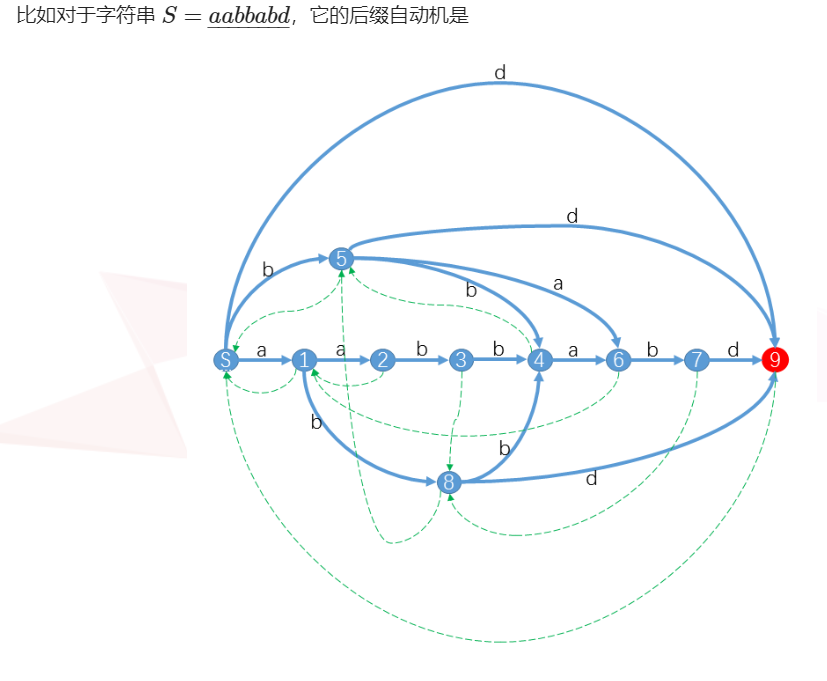
A few essential elements:

endpos(x): 它是一个集合, 表示一个子串的所有结束位置(可能有许多结束位置, 因为会有本质相同子串), 如果两个子串的$endpos$相同, 那么这两个子串属于一个"状态" , 同时他俩一个是另一个的后缀

len(x) : 对于一个状态所表示的一堆字符串, 他们最长的那个的长度, 同时这些字符串按长度排个序, 长度是连续的整数

后缀link:

设一个A状态如("abab", "bab", "ab") 那么"b"就是状态中没有的最长后缀, 即"abab"(或bab"等)的最长的且没有在该状态出现的后缀

那么我将A状态向"b"状态所在的B状态连有向边, 叫做link, 如果从一个状态不断的跳link, 那么就会遍历一个字符串的所有后缀

转移函数: 在一个状态的末尾加一个字符使它转向另一个状态, 可以证明在同一个状态的字符串在末尾加一个字符后还在同一个状态

下面来讲构造:

考虑从前往后一个一个加入字符, 即增量法, 这样就保证了每加一个字符都满足后缀自动机的性质

设当前最长串为S[1...i-1], 现在加一个字符S[i], 我们要干的事就是让它的所有后缀都能从起点开始走一条路径表示出来

S[1...i]肯定是一个新状态, 因为他是最长的, 设这个转态为np

因为前面S[1...i-1]已经构造好了, 我们从状态p = {s[1...i-1]}开始往前跳, 刚才说了, 往前跳的过程中会遍历它的所有后缀, 那么我们直接从以前的状态向他连一条边, 就可以从以前的状态转移到他了, 虽然这还是O($n^2$)的错误解法, 但给我们提供了不错的思路

设ch[s]['a'~'z']为它的转移函数, 如ch[s]['a']表示从s状态加一个'a'字符转移到哪个转态

设加入字符c, 向刚才一样跳link, 设到了状态A, 如果ch[A][c] == 0, 直接让ch[A][c] = np, 然后继续跳link, 最后如果跳到了根节点, 那他的link就是初始状态

    for (; p && !ch[p][c]; p = f[p]) ch[p][c] = np;
    if (!p) f[np] = 1;

如果碰到了ch[A][c] = q($q \not= 0$), 分两种情况

如果len(p) = len(q) + 1, 那么使q成为终止状态, np向q link一下

否则, 原先p中的字符串集就不再有相同的$endpos$, 因为从A转移过来的串也是S[1...n]的后缀, 所以这部分$endpos$会多一个(i), 这个状态就会分裂, 因此我们新建一个状态$nq$去让多出的部分转移, $p$将转移到$nq$, $nq$再转移到$np$, 同时$q$和$np$都将向$nq$ $link$

看看图理解一下(大佬讲的很好)

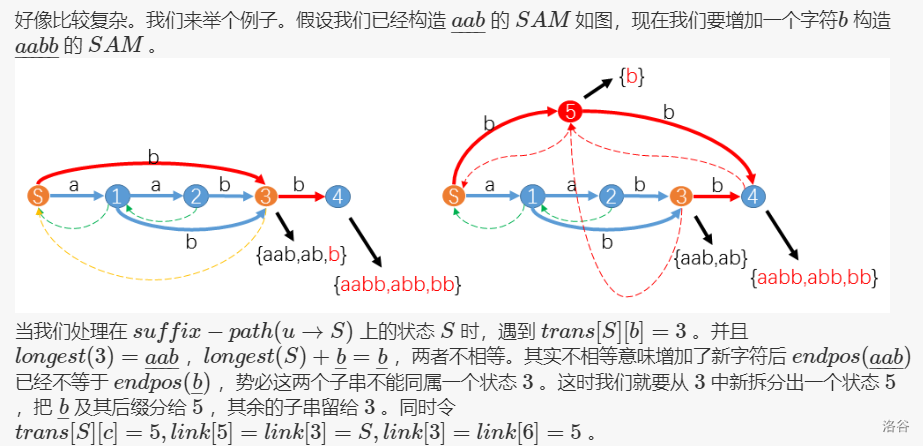
代码:

void add(int c) {
    int p = las, np = las = ++cnt; zhi[cnt] = 1;
    len[np] = len[p] + 1;
    for (; p && !ch[p][c]; p = f[p]) ch[p][c] = np;
    if (!p) f[np] = 1;
    else {
        int q = ch[p][c];
        if (len[q] == len[p] + 1) f[np] = q;
        else {
            int nq = ++cnt;
            for (int i = 0;i < 26; i++)
            ch[nq][i] = ch[q][i];
            len[nq] = len[p] + 1, f[nq] = f[q];
            f[q] = f[np] = nq;
            for (; p && ch[p][c] == q;p = f[p]) ch[p][c] = nq;
        }
    }
}