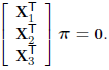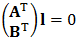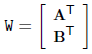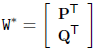1. The three-dimensional points in space
In the three-dimensional space P . 3 in a point (X-, the Y, the Z) T , its homogeneous coordinates four-element vector (X- . 1 , X- 2 , X- . 3 , X- . 4 ) T , can be normalized expressed as ((X- , the Y, the Z,. 1) T , if X- . 4 = 0, indicates that the point is infinity.
Three-dimensional space P . 3 projective transformation on the point, by a 4x4 matrix H is non-singular vector X by aligning the views obtained left, i.e., X '= HX. Wherein the transform matrix H has 15 degrees of freedom, plus an arbitrary scaling factor.
2. The plane of the three-dimensional space
The method of the two-dimensional space represents the similarity straight, plane three-dimensional space can be expressed by the following equation as
p 1 X + n 2 Y n + 3 Z + p 4 = 0
Thus homogeneous plane is expressed as = [pi] ([pi] . 1 , [pi] 2 , [pi] . 3 , [pi] . 4 ) T , which has three degrees of freedom. May be abbreviated formula
π T L = 0
This means that point = X-(X-, the Y, the Z,. 1) T is located on the plane π.
3. The planar nature
Three decided a plane. Has three linearly independent points X- I , for I = 1,2,. 3, they are located on a plane π, i.e. to meet the [pi] T X- I = 0. Stacking a matrix obtained
Thus the plane π is 3x4 matrix null space vector, can be in any ratio scale, it is uniquely determined.
Space in the plane P 2 of two points determined a straight line, the straight line l can be solved in addition to the zero vector space method, may also be obtained directly = x × y l by the cross product of the two point homogeneous. In the three-dimensional space P . 3 , it is also solved by a method analogous to the plane of the cross product.
Three planes that decision. Has three linearly independent plane [pi] I , for I = 1,2,. 3, they can be determined by the intersection of the formula X
Point X is the null space vector 3x4 matrix. This is a space plane P 2 of the two lines intersect at one point in three dimensional space P . 3 extension.
Projection transformation. Transformation point X '= lower HX, transform plane is expressed as:
p '= H -T p
to parameterize. One o'clock on the plane X can be written as π
X = Mx
Wherein each column of matrix M is a 4x3 [pi] T null space, i.e., [pi] T M = 0. 3 yuan while X represents the vector x in a two-dimensional space P 2 projected on, is parameterized point X.
4. The straight line in three-dimensional space
It may be defined as a straight line connecting two points, or the intersection of two planes. A point in three-dimensional space has three degrees of freedom two-dot chain lines A and B satisfies the following equation
Seen, this is a straight line l 2x4 matrix null space, it has four degrees of freedom (3x4 matrix null space since there are three degrees of freedom). In the space P . 3 in a degree of freedom of the object 4 is represented by homogeneous difficult because it is a five-element vector, the homogeneous plane and the points are represented by the 4-element vector. There are several ways to solve this problem represents the expression difficult.
FIG combination of straight lines. Three-dimensional space in a straight line directly above the 2x4 matrix W represented:
It contains a combination of two points, these two points as a group representative vector space spanned. The straight line is actually null space of W. On the other hand, the null space W must two linearly independent vectors group, assumed that the two groups are vectors P and Q, then WP = 0, and thus A T P = B T P = 0, P means It is a plane including the point a and point B. Q is a same plane comprising the point A and the point B. Therefore, the straight line is the intersection of these two planes, so that a straight line can be represented as a 2x4 matrix as follows:
It represents two plane-yl vector space spanned. The straight line is actually W * null space.
This combination representation can also be extended to the plane, e.g., a plane π alternatively be represented as a point and a straight line X of the combining matrix M W, i.e.,
Plane π is the null space of the matrix M. Matrix M is a 3x4 matrix, it may also be seen as a combination of three coplanar points.
The quadric surface in three-dimensional space (quadrics and dual quadrics)
Space P . 3 quadric surface is defined by the following formula:
XTQX = 0
Wherein Q is a symmetric 4x4 matrix, which is used to represent the quadratic surface.
Quadratic surface properties:
(1) a quadric nine degrees of freedom, plus a scale factor.
(2) determined by a quadric 9 linearly independent points.
(3) defines a quadric relation between the polarization plane and a point (similar to the two-dimensional space defined in a conic polarization relationship between a line and a point). Point X with respect to the pole plane Q is:
p = QX
(4) with a quadric Q plane π intersects a quadratic curve C.
(5) at the point of projection transformation X '= HX, was converted to a quadric
Q' = H-TQH-1
(6) a quadric dual is still a quadric. In the projective transformation point X '= HX, was converted to a dual quadric
Q*' = HQ*HT
Visible, dual quadric transform calculation easier than the transformation point quadric.