Activation function in the neural network is an important part, why the article describes the use of neural networks for network activation function, several common activation function (Logical the Sigmoid function, a hyperbolic tangent function tanh, a linear function of the rectifier (RELU), neural networks gradient disappears problems and how to avoid ReLU gradient disappears.
1 by reason of the activation function
If the neural network can extract nonlinear features no convolution operation, the neural network and do not activate the function, then the neural network output layer i only Wxi + b. Thus this neural network regardless of how many layers, the output of the i-layer is a layer on the i-th input xi is the linear combination, this time corresponds to a multilayer neural network is a multilayer degenerate linear regression model, such as the image is difficult to learn, wherein the complex data audio, text and so on.
For this reason, the neural network to introduce non-linear activation function to add some features to the neural network, we now have a common activation functions are mostly non-linear function. Such a neural network layer obtained at the input is no longer linear combination.
2 common activation function
2.1 Logic Function Sigmoid [1]
Logic function (logistic function) or logistic curve (logistic curve) is a common function of S, when it was named Pierre Francois Wei Lvle in 1844 or 1845 in the study of its relationship with the population growth of.
Logistic function of a simple expression is:
\[ f\left( x \right) = \frac{1}{{1 + {e^{ - x}}}} \]
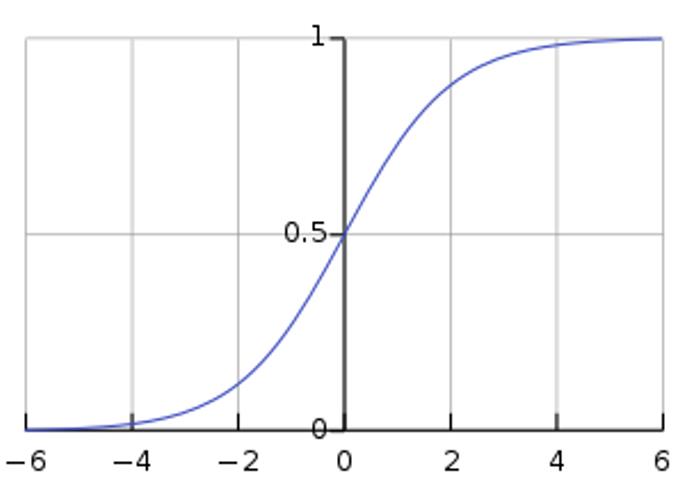
FIG image standard logic function 1
Form logic functions such as S, it is often called S-shape function.
The image is easy to know the function f (x) is the domain of [-∞, + ∞], is the range (0,1)
For f (x) the derivative, readily available
\[f'\left( x \right) = {\left( {\frac{1}{{1 + {e^{ - x}}}}} \right)^\prime } = \frac{{{e^{ - x}}}}{{{{\left( {1 + {e^{ - x}}} \right)}^2}}}\;\; = f\left( x \right)\left( {1 - f\left( x \right)} \right)\]
2.2 hyperbolic tangent function tanh [2]
Hyperbolic tangent function is a hyperbolic function. In mathematics, a hyperbolic function is a kind of common trigonometric functions and the like. Hyperbolic tangent function is defined as
\[f\left( x \right) = \tanh \left( x \right) = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}\]
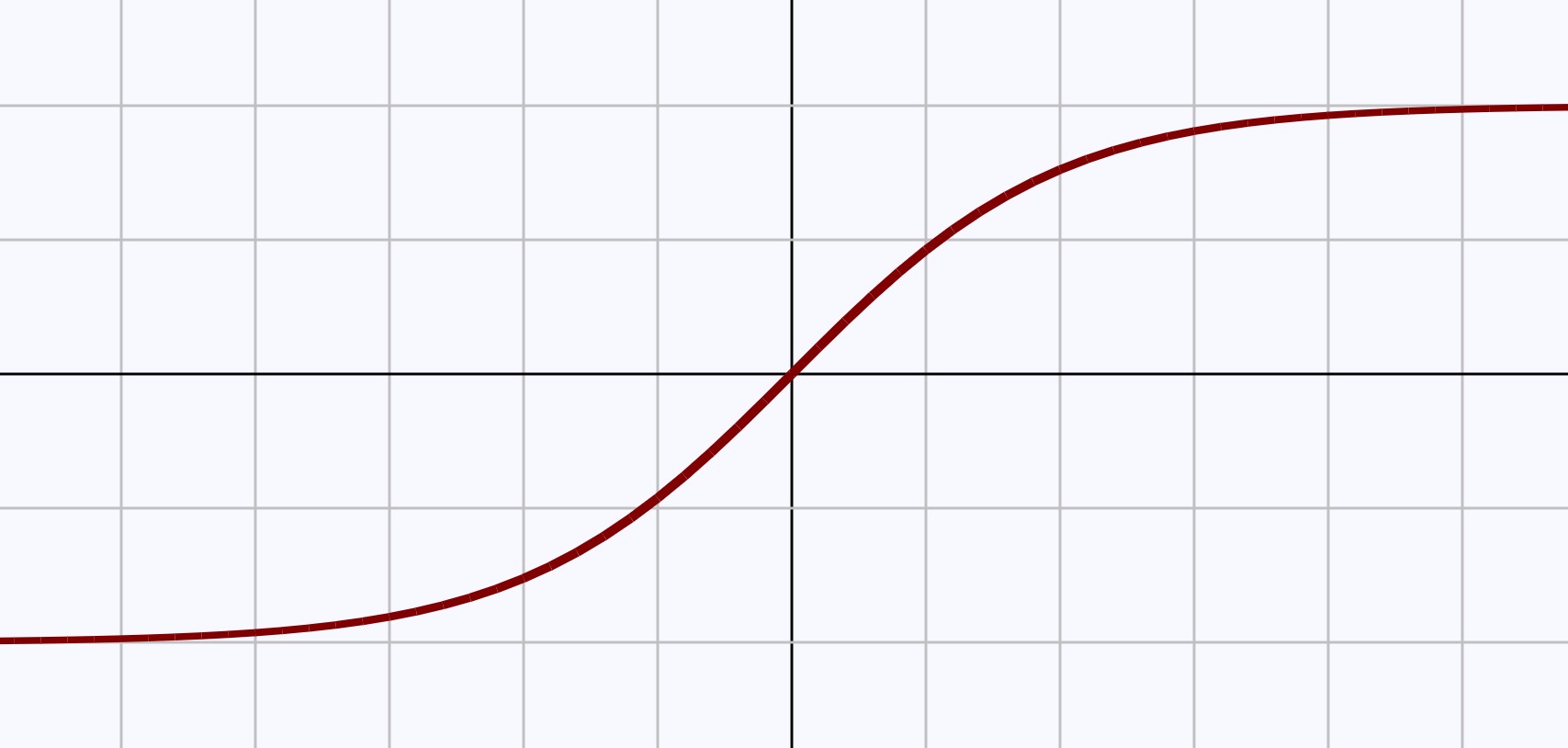
The second image (with a similar logic function) hyperbolic tangent function of FIG.
The image is easy to know the function f (x) is the domain of [-∞, + ∞], is the range (-1,1)
For f (x) the derivative, readily available
\[f'\left( x \right) = {\left( {\frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}} \right)^\prime } = \frac{4}{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2}}}\;\; = 1 - f{\left( x \right)^2}\]
2.3 Linear rectifying function ReLU [3]
Rectifying linear function (Rectified Linear Unit, ReLU), also known as linear correction means is an artificial neural network used in activation function, generally refers to a ramp function and a nonlinear function represented by variants.
In general sense, linear algebra rectifying function refers to the ramp function, that is,
\[f\left( x \right) = \left\{ \begin{array}{l} x\quad \quad x \ge 0 \\ 0\quad \quad x < 0 \\ \end{array} \right.\]
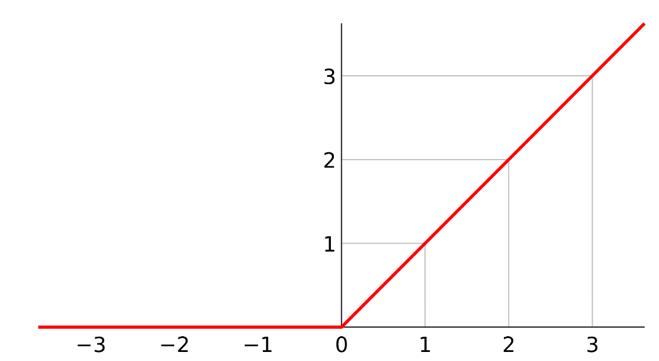
图3 ReLU函数图像
从函数图像易知f(x)的定义域为[-∞, +∞], 值域是[0, +∞)
对f(x)求导数,易得
\[f'\left( x \right) = \left\{ \begin{array}{l} 1\quad \quad x \ge 0 \\ 0\quad \quad x < 0 \\ \end{array} \right.\]
3 梯度消失问题和ReLU如何处理此问题
使用S形函数作为激活的神经网络中,随着神经网络的层数增加,神经网络后面层在梯度下降中求导的梯度几乎为0,从而导致神经网络网络后面层的权值矩阵几乎无法更新。表现为随着隐藏层数目的增加,分类准确率反而下降了。这种现象叫做消失的梯度问题。
假设神经网络只有三层,用S型函数作为激活函数
第一层输入为x, 输出为S(W1x+b1)
第二层输入为S(W1x+b1),输出为S(W2S(W1x+b1)+b2)
第三层输入为S(W2S(W1x+b1)+b2),输出为S(W3S(W2S(W1x+b1)+b2)+b3)
同时简记住每层在激活函数处理前的值为ai, 输出为fi
假设最后损失函数为L,L是一个关于f3的函数,那么求导易得
\[\begin{array}{l} \frac{{\partial L}}{{\partial {W_1}}} = \frac{{\partial L}}{{\partial {f_3}}} \cdot \frac{{\partial S\left( {{W_3}S\left( {{W_2}S\left( {{W_1}x + {b_1}} \right) + {b_2}} \right) + {b_3}} \right)}}{{\partial {W_1}}} \\ \quad \quad = \frac{{\partial L}}{{\partial {f_3}}} \cdot \frac{{\partial S}}{{\partial {a_3}}} \cdot \frac{{\partial {W_3}S\left( {{W_2}S\left( {{W_1}x + {b_1}} \right) + {b_2}} \right) + {b_3}}}{{\partial {W_1}}} \\ \quad \quad = \frac{{\partial L}}{{\partial {f_3}}} \cdot \frac{{\partial S}}{{\partial {a_3}}} \cdot {W_3} \cdot \frac{{\partial S\left( {{W_2}S\left( {{W_1}x + {b_1}} \right) + {b_2}} \right)}}{{\partial {W_1}}} \\ \quad \quad = \cdots \\ \quad \quad = \frac{{\partial L}}{{\partial {f_3}}} \cdot \frac{{\partial S}}{{\partial {a_3}}} \cdot {W_3} \cdot \frac{{\partial S}}{{\partial {a_2}}} \cdot {W_2} \cdot \frac{{\partial S}}{{\partial {a_1}}} \cdot \frac{{\partial {a_1}}}{{\partial {W_1}}} \\ \end{array}\]
其中偏导数∂S/ ∂ai是造成梯度消失的原因,因为S函数的导数阈值为
\[f'\left( x \right) = \frac{{{e^{ - x}}}}{{{{\left( {1 + {e^{ - x}}} \right)}^2}}}\;\; \in \left( {0,\left. {\frac{1}{4}} \right]} \right.\]
即有0<∂S/ ∂a1≤0.25, 0<∂S/ ∂a2≤0.25, 0<∂S/ ∂3≤0.25, 在损失函数偏导表达式中三个偏导数相乘有:
\[0 < \frac{{\partial S}}{{\partial {a_3}}}\frac{{\partial S}}{{\partial {a_2}}}\frac{{\partial S}}{{\partial {a_1}}} \le 0.015625\]
这样会减小损失函数的数值,如果神经网络是20层,则有
\[0 < \frac{{\partial S}}{{\partial {a_{20}}}}\frac{{\partial S}}{{\partial {a_{19}}}} \cdots \frac{{\partial S}}{{\partial {a_1}}} \le {0.25^{20}} = {\rm{9}}.0{\rm{94}} \times {10^{ - 13}}\]
这是一个更小的数,所以神经网络后几层求第一层参数W1的梯度就非常小。而ReLU函数就是为了避免梯度消失问题,因为ReLU求导只有两个值1或0,这样的话只要神经网络梯度中一条路径上的导数都是1,那么无论网络有多少层,网络后几层的梯度都可以传播到网络前几层。