【Problem Description】
A traveler can have a maximum of m kg backpack, there are n items, their weight are W1, W2, ..., Wn, their value are C1, C2, ..., Cn. If only one of each item traveler seeking to get the maximum total value.
[Input Format]
The first line: two integers, M (capacity backpack, M <= 200), and N (the number of items, N <= 30); a first 2..N + 1 rows: two integers each line Wi, Ci, each represents a weight and value items.
[Output format]
Only one line, a number that indicates the maximum total value.
[Sample input] package.in
10 4 2 1 3 3 4 5 7 9
[Sample output] package.out
12
f[i][v]=max{ f[i-1][v] , f[i-1][v-w[i]]+c[i] }。
Initial f [0] [0] = 0, the remainder is negative infinity, the target: max {f [n] [j]} 0 <= j <= m

(Optimized spatial complexity)
By the state transition equation of the DP, the state of each stage i is found only with the stage i-1 related condition. In this case, we can use the optimization method called "scroll array", reducing overhead space.
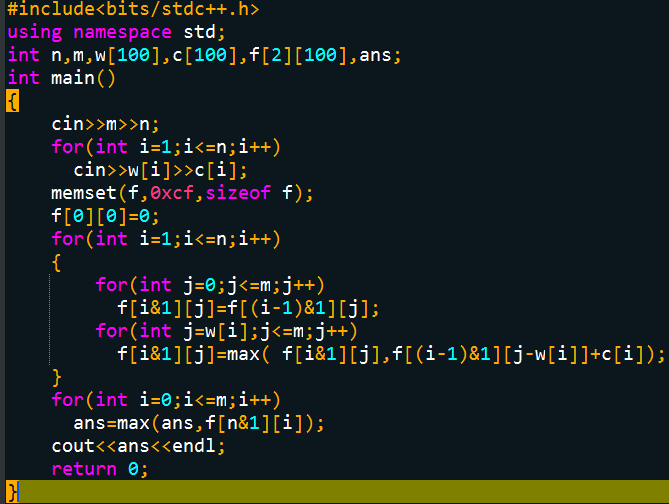
(Continue to optimize the spatial complexity)
Time and space complexity of the above process are O (N * V), wherein the basic time complexity can no longer be optimized, but it may be optimized spatial complexity to O (V).
How to first consider speaking above Thinks, there is definitely a main loop i = 1..N, each calculated two-dimensional array f [i] [0..V] of all values. Well, if only one array f [0..V], can not guarantee the end of the i-th cycle f [v] said is that we define the state of f [i] [v] it? f [i] [v] is f [i-1] [v] and f [i-1] [vw [i]] recursion from two sub-problems, can guarantee the push f [i] [v ] is (i.e. the i-th main loop, push [v] can be obtained when f [i-1] [v] and f [i-1] [vw [i f)]] value of it? In fact, this requires us to each main loop reverse push v = f [v] V..0, so as to ensure the f [vw [i]] is pushed f [v] stored state is f [i -1] value [vw [i]] of.
Pseudo-code as follows:
for i=1..N
for v=V..0
f[v]=max{f[v],f[v-w[i]]+c[i]};
其中f[v]=max{f[v],f[v-w[i]]+c[i]}相当于转移方程f[i][v]=max{f[i-1][v],f[i-1][v-w[i]]+c[i]},因为现在的f[v-w[i]]就相当于原来的f[i-1][v-w[i]]。如果将v的循环顺序从上面的逆序改成顺序的话,那么则成了f[i][v]由f[i][v-w[i]]推知,与本题意不符,但它却是另一个重要的完全背包问题最简捷的解决方案,故学习只用一维数组解01背包问题是十分必要的。
【解法一】
设f[i][v]表示前i件物品,总重量不超过v的最优价值,则f[i][v]=max(f[i-1][v-w[i]]+c[i],f[i-1][v]) ;f[n][m]即为最优解
给出程序:
1 #include<cstdio> 2 using namespace std; 3 const int maxm = 201, maxn = 31; 4 int m, n; 5 int w[maxn], c[maxn]; 6 int f[maxn][maxm]; 7 8 int max(int x,int y) { x>y?x:y;} //求x和y最大值 9 10 int main(){ 11 scanf("%d%d",&m, &n); //背包容量m和物品数量n 12 for (int i = 1; i <= n; i++) //在初始化循环变量部分,定义一个变量并初始化 13 scanf("%d%d",&w[i],&c[i]); //每个物品的重量和价值 14 for (int i = 1; i <= n; i++) // f[i][v]表示前i件物品,总重量不超过v的最优价值 15 for (int v = m; v > 0; v--) 16 if (w[i] <= v) f[i][v] = max(f[i-1][v],f[i-1][v-w[i]]+c[i]); 17 else f[i][v] = f[i-1][v]; 18 printf("%d",f[n][m]); // f[n][m]为最优解 19 return 0; 20 }
使用二维数组存储各子问题时方便,但当maxm较大时,如maxm=2000时不能定义二维数组f,怎么办,其实可以用一维数组。
【解法二】
本问题的数学模型如下:设 f[v]表示重量不超过v公斤的最大价值, 则f[v]=max{f[v],f[v-w[i]]+c[i]} ,当v>=w[i],1<=i<=n 。
程序如下:
1 #include<cstdio> 2 using namespace std; 3 4 const int maxm = 2001, maxn = 31; 5 int m, n; 6 int w[maxn], c[maxn]; 7 int f[maxm]; 8 int main(){ 9 scanf("%d%d",&m, &n); //背包容量m和物品数量n 10 for (int i=1; i <= n; i++) 11 scanf("%d%d",&w[i],&c[i]); //每个物品的重量和价值 12 13 for (int i=1; i <= n; i++) //设f(v)表示重量不超过v公斤的最大价值 14 for (int v = m; v >= w[i]; v--) 15 if (f[v-w[i]]+c[i]>f[v]) 16 f[v] = f[v-w[i]]+c[i]; 17 printf("%d",f[m]); // f(m)为最优解 18 return 0; 19 }
总结
01背包问题是最基本的背包问题,它包含了背包问题中设计状态、方程的最基本思想,另外,别的类型的背包问题往往也可以转换成01背包问题求解。故一定要仔细体会上面基本思路的得出方法,状态转移方程的意义,以及最后怎样优化的空间复杂度。