Solution: fantasy strategy game Township
Original title: Portal
to fixed weights, find a tree that all point to the path of right * and minimum values. Online modification requires the right point, online answer.
If it is purely static queries, we can cure do with dotted. But the dynamic of it? The total can not be modified once to do a dotted bar, the complexity will reach \ (O (the n-^ 2logn) \) . That we do not use the partition point yet? No, we have a dynamic point divide and conquer!
Front: dotted tree
The entire tree structure is unchanged, modified only point right. So, we have every point to the sorting center of gravity is constant (premise dynamic point of partition) . If the point of partition between us every election to the center with an edge, can constitute a logn height of the tree.
This tree is our dotted tree (dynamic point divide and conquer) .
Dotted tree are: For the current tree rooted at u, find its center of gravity, the center of gravity to delete, and then for each of them sub-tree recursively sub-processes, and the center of gravity and the center of gravity of the sub-tree u even edge. Only need to add a partition on the original board fa[rt]=u;
to modify Well, usually directly in dotted tree jump up on the line.
Here directly apply lsy Gangster code:
inline void work(int u,int father){
vis[u]=1,fa[u]=father;
for(int i=head[u];i;i=nex[i]){
int v=var[i];
Size=siz[v];rt=0;
getroot(v,u);
Addedge(u,rt,v);
work(rt,u);
}
}Symbolic Addedge, because we may need to distinguish between sub-tree dotted the tree a certain point, we can record through Addedge v to distinguish.
For each node of the tree dotted, holds information in all of its sub-tree, and then, for each modification, we jumped up from the current node in the tree dotted, time complexity is logn (after all, the point high points of the tree does not exceed log n).
So for this question it?
First draw a diagram to help understand:
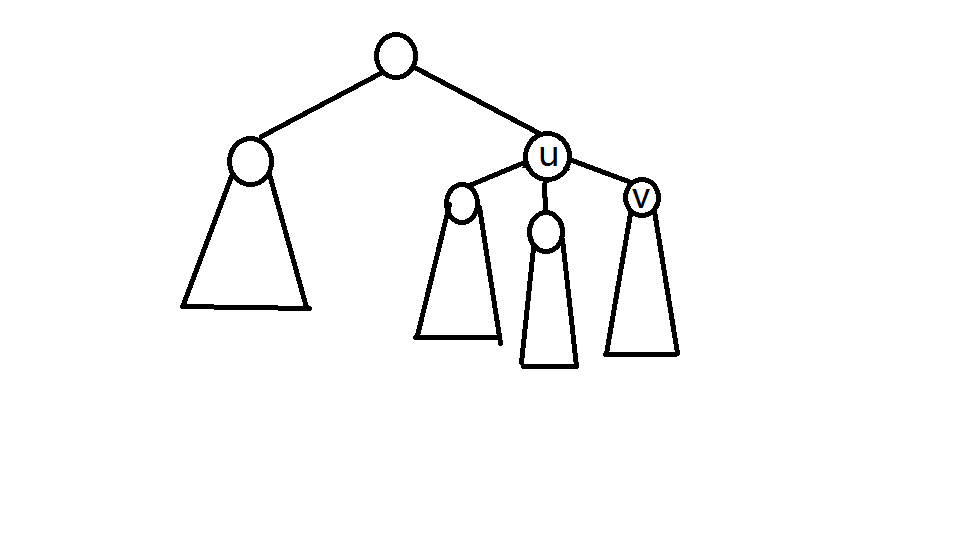
Q1: statistics answer
We know that the point of partition statistics answer is usually to find the center of gravity in the sub-tree then the inclusion-exclusion, then the dynamic point divide and conquer it?
Still similar.
We assume that all the nodes in the sub-tree v v answers have good statistics, u now requires all children in addition to the other nodes in the tree outside the v and its sub-tree of v to answer.
The drawing, gestures?
SUM [u] represents the weight of all the nodes in the point u and the root tree.
After u find the answer, we have to eliminate the influence of v and its sub-tree for answers, plus \ ((SUM [u] -sum [v]) * dist (u, v) \) .
You may wish to define two arrays ans, ansf.
all subtrees ANS [u] represents a u-u in the node point of the path points and the right *.
Path all subtrees ANSF [v] represents the v (of course including a v) of the point v to the parent node (i.e., u) and a point * Right.
ans [u] -ansf [v] that is, all subtrees u removing nodes other than the sub-tree v and v u point to answer.
Still inclusion and exclusion.
\[ ans[u]-ansf[v]+(sum[u]-sum[v])*dist(u,v) \]
Then seek contribution from outside the node u and its sub-tree node to answer it? For applications that need a parent node in the tree jump point, and then repeat the process again.
inline ll calc(int x){
ll ret=ans[x];
for(int i=x;p[i];i=p[i]){
ll l=dis(p[i],x);
ret+=ans[p[i]]-ansf[i];
ret+=(sum[p[i]]-sum[i])*l;
}
return ret;
}The revised points right, we just need to jump in dotted the trees, you can maintain three arrays.
Q2: Update optimal solution
So, problem solved? No! After testing, we found that if you start looking for answers every time from the root words will T, will be stuck into \ (O (the n-^ 2) \) . How to do it?
The solution is: from the last point to start looking for answers.
Or above that figure, we move from u to v, then u in the sub-tree, the amount of change to the answer is
\ [\ Delta ans = (sum [u] -sum [v]) * dist (u, v ) - sum [v] * dist
(u, v) \] is \ (\ of Delta ANS = (SUM [U] -2 * SUM [V]) * dist (U, V) \) .
Obviously, only if \ (sum [v]> sum [u] / 2 \) , the only answer may become more excellent. And this point, at most one.
Therefore, we can use directly answer a query to update the answer, specifically, is to scan each point in turn adjacent to it, to the point and answer better to update, and then repeat until the optimal solution is found .
inline ll query(int x){
ll anss=calc(x);
for(int i=head[x];i;i=nex[i]){
int v=var[i];
ll tmp=calc(v);
if(tmp<anss) return query(v);//更新最优解
}
last=x;return anss;
}Learn a little slide down the tree RMQ, but still a little mystery.
Code implementation draws the Gangster: https://blog.csdn.net/qq_34564984/article/details/53791482
#include<bits/stdc++.h>
#define ll long long
const int N=1e5+1;
using namespace std;
bool vis[N];
int n,Q,rt,cnt,last=1,Size,f[N],p[N],s[N<<1],id[N],ip[N],dep[N<<1],siz[N],st[N<<1][20];
ll ans[N],ansf[N],dist[N<<1],sum[N];
int head[N],nex[N<<1],var[N<<1],edge[N<<1];
template<typename S>inline void in(S &r){//快读
r=0;int f=1;char c='a';
do{c=getchar();if(c=='-') f=-1;}while(!isdigit(c));
do{r=(r<<3)+(r<<1)+c-'0';c=getchar();}while(isdigit(c));
r*=f;
}
inline void add(int x,int v,int w){//加边
var[++cnt]=v,edge[cnt]=w,nex[cnt]=head[x],head[x]=cnt;
}
inline void gr(int x,int fa){//找重心
siz[x]=1,f[x]=0;
for(int i=head[x];i;i=nex[i]){
int v=var[i];
if(vis[v]||v==fa) continue;
gr(v,x);
siz[x]+=siz[v],f[x]=max(f[x],siz[v]);
}
f[x]=max(f[x],Size-siz[x]);
if(f[x]<f[rt]) rt=x;
}
inline void build(int x){//建点分树
vis[x]=1;
for(int i=head[x];i;i=nex[i]){
int v=var[i];
if(vis[v]) continue;
Size=siz[v],rt=0;
gr(v,0);p[rt]=x;
build(rt);
}
}
inline void dfs(int x,int fa){
s[++cnt]=x;
if(!id[x]) id[x]=cnt;
dep[cnt]=dep[ip[fa]]+1;ip[x]=cnt;
for(int i=head[x];i;i=nex[i]){
int v=var[i];
if(v==fa) continue;
dist[v]=dist[x]+edge[i];
dfs(v,x);s[++cnt]=x,dep[cnt]=dep[ip[fa]+1];
}
}
inline void make(){
for(int i=1;i<=cnt;++i) st[i][0]=i;
for(int j=1;j<=18;++j)
for(int i=1;i<=cnt;++i) if(i+(1<<j)-1<=cnt){
int x=st[i][j-1],y=st[i+(1<<j-1)][j-1];
if(dep[x]<dep[y]) st[i][j]=x;
else st[i][j]=y;
}
}
inline int query2(int l,int r){
int len=r-l+1,i=0;
while((1<<i+1)<=len) ++i;
if(dep[st[l][i]]<dep[st[r-(1<<i)+1][i]]) return st[l][i];
else return st[r-(1<<i)+1][i];
}//O(1)LCA
inline int lca(int x,int y){
if(id[x]>id[y]) swap(x,y);
return s[query2(id[x],id[y])];
}
inline ll dis(int x,int y){
int c=lca(x,y);
return dist[x]+dist[y]-2*dist[c];
}//LCA求路径长
inline void update(int x,int val){
sum[x]+=val;
for(int i=x;p[i];i=p[i]){
ll l=dis(p[i],x);
sum[p[i]]+=val;//p[i]子树中总的点权
ansf[i]+=val*l;//i子树中所有节点到他爹的距离
ans[p[i]]+=val*l;//p[i]子树中所有节点到他的距离
}
}
inline ll calc(int x){
ll ret=ans[x];
for(int i=x;p[i];i=p[i]){
ll l=dis(p[i],x);
ret+=ans[p[i]]-ansf[i];//核心
ret+=(sum[p[i]]-sum[i])*l;
}
return ret;
}
inline ll query(int x){
ll anss=calc(x);
for(int i=head[x];i;i=nex[i]){
int v=var[i];
ll tmp=calc(v);
if(tmp<anss) return query(v);//更新最优解
}
last=x;return anss;
}
int main(){
in(n),in(Q);
for(int i=1,a,b,c;i<n;++i){
in(a),in(b),in(c);
add(a,b,c),add(b,a,c);
}
cnt=0;dfs(1,0);make();//LCA套装
Size=f[0]=n;
gr(1,0);build(rt);//建点分树
int a,b;
while(Q--){
in(a),in(b);
update(a,b);//更新当前节点值
printf("%lld\n",query(last));//从上一次的最优解开始寻找
}
return 0;
}