Table of contents
2. Binary tree concept and structure
2.4 Properties of binary trees
2.5 Storage structure of binary tree
3.1 Why talk about heap separately?
3.2 Concept and structure of heap
3.2.2 Heap downward adjustment algorithm
3.2.3 Heap upward adjustment algorithm
3.2.4 Use the downward adjustment algorithm to build a large heap
3.2.4.1 The time complexity of using downward adjustment algorithm: O(N).
3.2.4.2 Time complexity of using upward adjustment algorithm: O(NlogN)
3.4.2 Use heap to solve TOP-K problem
Foreword
The goal of this chapter is to learn the concept and structure of trees, the concept and structure of binary trees, and finally use code to implement heaps. If you are very familiar with the concepts and properties of trees and binary trees, you can jump directly to the heap part. A heap is a special type of binary tree in which the value of each node is greater than or equal to the value of its child nodes. This property is called a heap property.
1. Tree concept and structure
1.1 Concept of tree
Tree is a non-linear data structure, which is a set of hierarchical relationships composed of n (n>=0) limited nodes. It's called a tree because it looks like an upside-down tree, which means it has the roots pointing up and the leaves pointing down.
- There is a special node called the root node, and the root node has no predecessor nodes.
- Except for the root node, the other nodes are divided into M (M>0) disjoint sets T1, T2,..., Tm, where each set Ti (1<= i <= m) is another tree structure. A subtree similar to a tree. The root node of each subtree has one and only one predecessor, and can have 0 or more successors.
- Therefore, the tree is defined recursively.
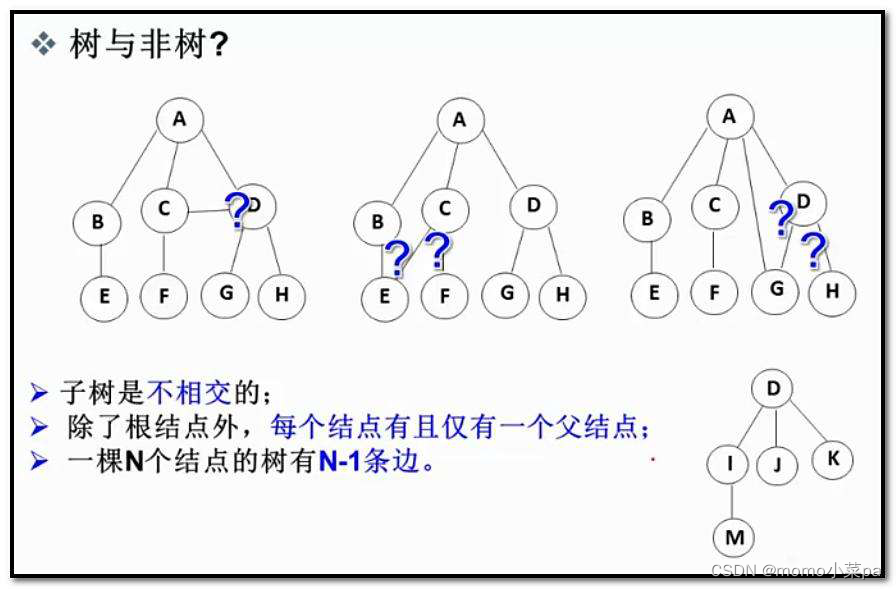
Note: In the tree structure, there cannot be intersection between subtrees, otherwise it will not be a tree structure.
1.2 Related concepts of trees
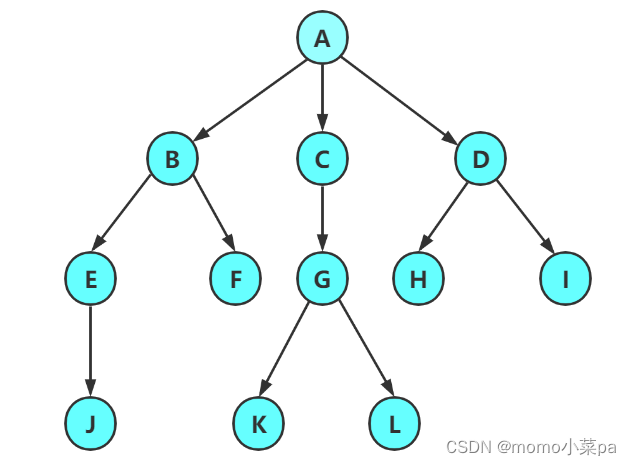
Degree of node:The number of subtrees contained in a node is called the degree of the node; As shown in the figure above: A is 6
Leaf node or terminal node: A node with degree 0 is called a leaf node; As shown in the figure above: Nodes such as B, C, H, I... are leaf nodes
Non-terminal nodes or branch nodes:Nodes with a degree other than 0; As shown in the figure above: nodes such as D, E, F, G... are branch nodes
Parent node or parent node:If a node contains child nodes, this node is called the parent node of its child node;
As shown above: A is the parent node of B
Child node or child node:The root node of the subtree contained by a node is called the child node of the node;
As shown above: B is a child node of A
Sibling nodes:Nodes with the same parent node are called sibling nodes; as shown above: B and C are sibling nodes
The degree of the tree:In a tree, the degree of the largest node is called the degree of the tree; as shown above: the degree of the tree is 6
Node level:Starting from the definition of the root, the root is the 1st level, the root's child nodes are the 2nd level, and so on;
The height or depth of the tree:The maximum level of nodes in the tree; As shown above: the height of the tree is 4
Cousin nodes:Nodes whose parents are on the same level are cousins of each other; as shown in the figure above: H and I are brother nodes of each other
The ancestors of the node:All nodes on the branches from the root to the node; as shown in the figure above: A is the ancestor of all nodes
Descendants:Any node in the subtree rooted at a node is called a descendant of that node.
As shown above: all nodes are descendants of A
Forest:A collection of m (m>0) disjoint trees is called a forest;
1.3 Representation of tree
The tree structure is more complicated than the linear table, and it is more troublesome to store and represent it. Since the value range is saved, the relationship between the nodes must also be saved. , In fact, there are many ways to represent trees, such as parent representation, child representation, child parent representation, and child brother representation, etc. Here we will briefly understand the most commonly usedchild brother representation
typedef int DataType; struct Node { struct Node* _firstChild1; // 第一个孩子结点 struct Node* _pNextBrother; // 指向其下一个兄弟结点 DataType _data; // 结点中的数据域 };
1.4 The practical application of trees (representing the directory tree structure of the file system)
2. Binary tree concept and structure
2.1 Concept
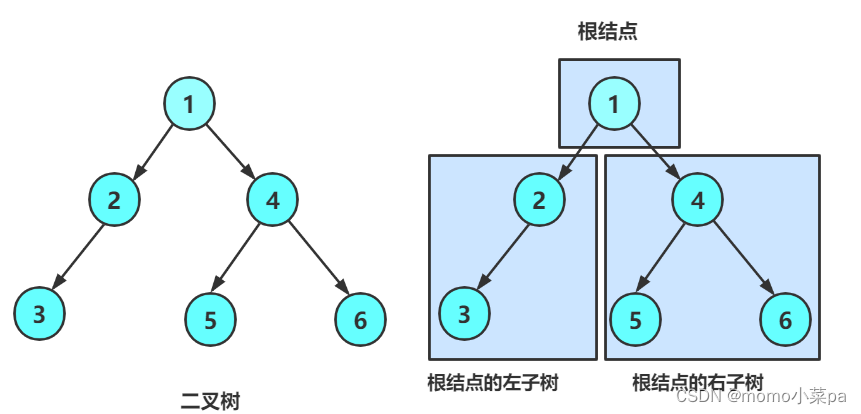
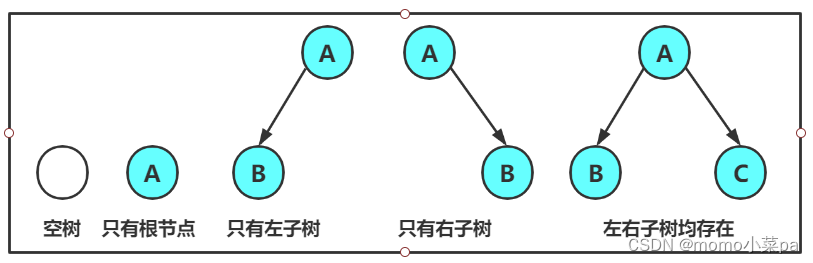
A binary tree is a finite set of nodes. The set is:
1. Or empty
2. Added by a root node Composed of two binary trees, also called left subtree and right subtree
As can be seen from the picture above:
1. There is no node with degree greater than 2 in a binary tree
2. The subtrees of a binary tree are divided into left and right subtrees, and the order cannot be reversed, so the binary tree is an ordered treeNote: Any binary tree is composed of the following situations:
2.2 Binary tree in reality:
2.3 Special binary tree:
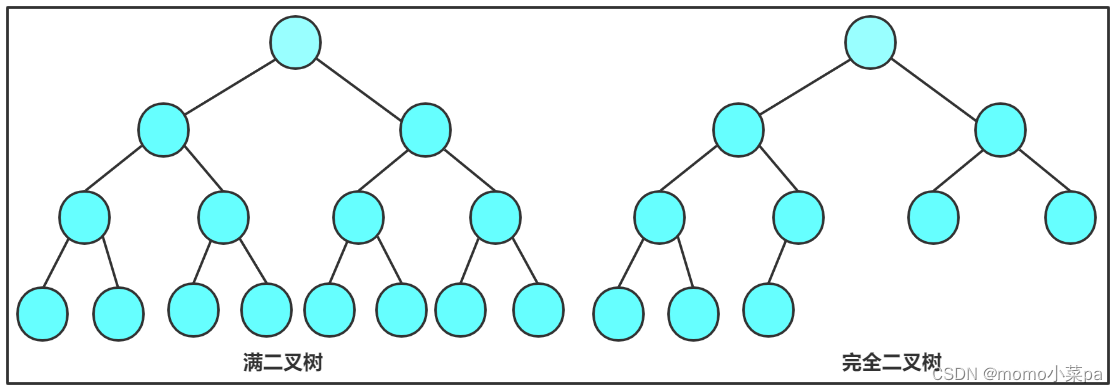
1. Full binary tree:A binary tree, if the number of nodes in each layer reaches the maximum, then the binary tree is a full binary tree. That is to say, if the number of levels of a binary tree is K and the total number of nodes is , then it is a full binary tree.
2. Complete binary tree: A complete binary tree is a very efficient data structure, and a complete binary tree is derived from a full binary tree. For a binary tree with depth K and n nodes, it is called a complete binary tree if and only if each node corresponds one-to-one with the nodes numbered from 1 to n in the full binary tree with depth K. It should be noted that a full binary tree is a special kind of complete binary tree.
In a complete binary tree, all levels except the last level are full, but they are continuous from left to right. The picture below is not continuous, so it is not a complete binary tree.
2.4 Properties of binary trees
1. If the number of levels of the root node is specified to be 1, then there will be at most one node on the i-th level of a non-empty binary tree.
2. If the number of levels of the root node is specified The number of levels is 1, then the maximum number of nodes of a binary tree with depth h is.
3. For any binary tree, if the degree is 0, the number of leaf nodes is, and the degree is 2 The number of branch nodes is, then = +1
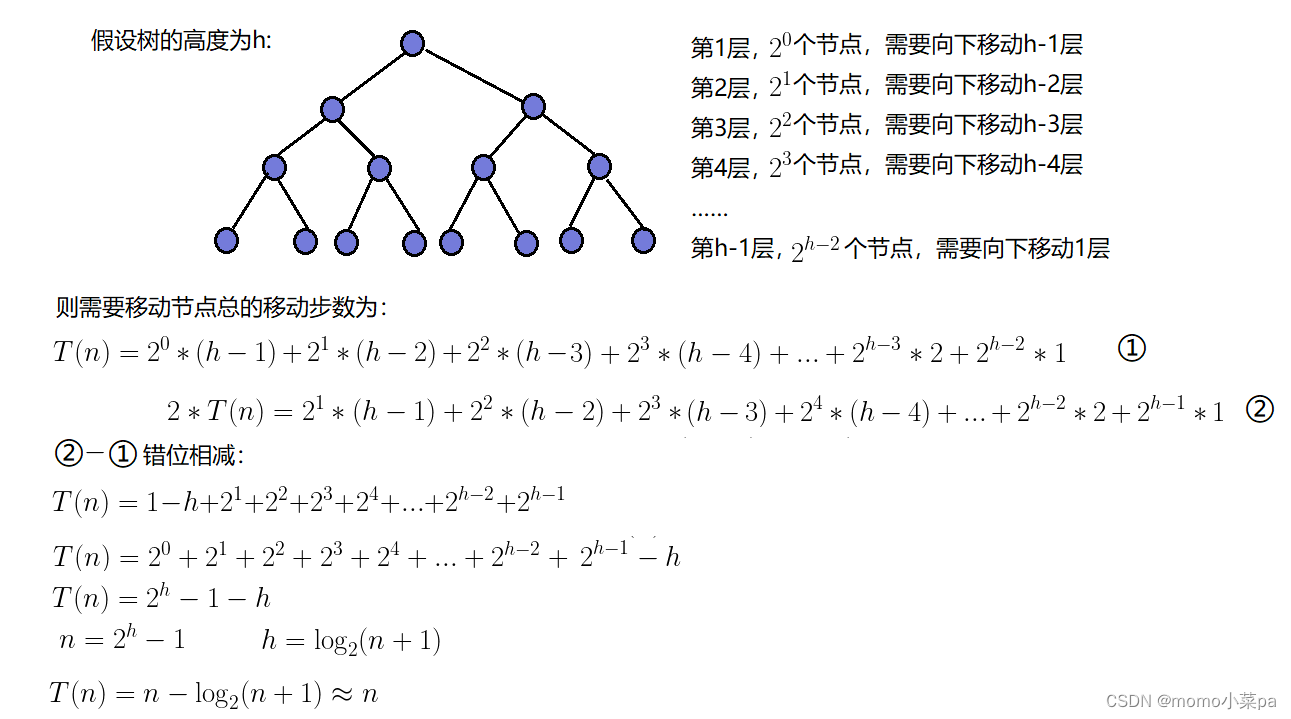
4. If the number of levels of the root node is 1, the depth of a full binary tree with n nodes,h= (ps: log is base 2, n+1 is logarithm)
5. For a complete binary tree with n nodes, if from top to In the array sequence from left to right below, all nodes are numbered starting from 0. Then for the node with serial number i:1. If i>0, the parent number of the node at position i: (i-1)/2; i=0, i is the root node number, there is no parent node
2 . If 2i+1<n, the left child number: 2i+1, 2i+1>=n otherwise there is no left child
3. If 2i+2<n, the right child number: 2i+ 2, 2i+2>=n otherwise there is no right child
2.5 Storage structure of binary tree
Binary trees can generally be stored using two structures, a sequential structure and a chain structure.
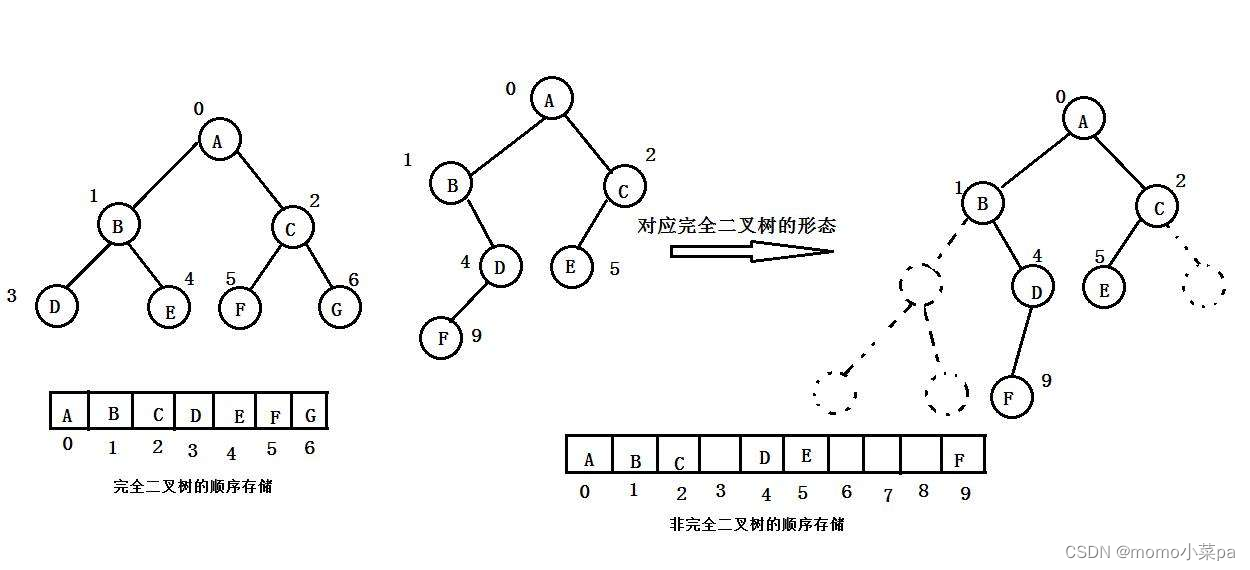
1. Sequential storage
Sequential structure storage uses arrays for storage. Generally, arrays are only suitable for representing complete binary trees, because if they are not complete binary trees, there will be a waste of space. In reality, only heaps use arrays for storage. We will explain specifically about heaps in the following chapters. The sequential storage of binary trees is physically an array and logically a binary tree.
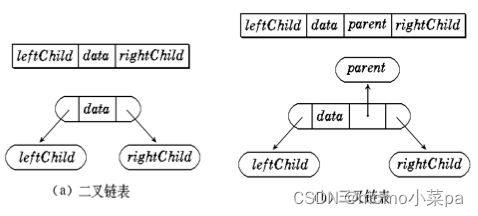
2. Linked storage
The linked storage structure of a binary tree means that a linked list is used to represent a binary tree, that is, a chain is used to indicate the logical relationship of elements. The usual method is that each node in the linked list consists of three fields, the data field and the left and right pointer fields. The left and right pointers are used to give the storage addresses of the link points where the left child and right child of the node are located respectively. Chain structures are divided into binary chains and trifurcated chains. Currently, we are generally learning binary chains. In later courses, we will learn about high-order data structures such as red-black trees and trifurcated chains.
3.Heap
3.1 Why talk about heap separately?
Heap is a special complete binary tree. Heap is special in that it has applications in many algorithms, such as heap sort, priority queue and union search. The heap is important because it enables efficient insertion and deletion operations. Therefore, we will take out the heap separately and talk about it.
3.2 Concept and structure of heap
Properties of heap:
- The value of a node in the heap is always no greater than or no less than the value of its parent node;
- The heap is always a complete binary tree.
3.3 Implementation of heap
3.2.1 Establishment of heap
Below we give an array. This array can be logically regarded as a complete binary tree, but it is not yet a heap. Now we use an algorithm to build it into a heap. The left and right subtrees of the root node are not heaps. How do we adjust them? Two algorithms are involved here: downward adjustment algorithm and upward adjustment algorithm.
Created using a sequence table, the members are as follows:
typedef struct Heap { HPDataType* a; int size; int capacity; }HP;
3.2.2 Heap downward adjustment algorithm
The upward adjustment algorithm is generally used when deleting data from the heap, and can also be used directly to build a heap. Now we are given an array, which is logically viewed as a complete binary tree. The downward adjustment algorithm of the heap refers to adjusting a node downward so that it meets the properties of the heap. The heap downward adjustment algorithm is as follows:
1. Starting from the root node, adjust each node downwards.
2. Compare the current node with its two child nodes. If the value of the current node is less than the larger value of the two child nodes, exchange the values of the current node and the larger child node.
3. Repeat step 2 until the current node reaches a leaf node.
Look at the code:
void AdjustDown(int* a, int size, int parent) { int child = parent * 2 + 1; while (child < size) { if (child+1 < size && a[child + 1] < a[child]) { ++child; } if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } else { break; } } }There are several details that need to be paid attention to when writing this algorithm:
1. How to find child nodes.
2. Which child to exchange with
3. Conditions for ending the exchange
1. When we look for children, we multiply the parent node by 2 to find the left child, and add 1 to the left child to find the right child.
2. If you want to build a large pile, you have to exchange with the child with a larger value. If you want to create a small pile, just exchange with the smaller child. What needs to be noted here is that not all parent nodes have right children. In this case, it is necessary to determine whether the right child exists. child+1 < size
3. To perform the exchange, just ensure that the child node is within the total data range. child < size
3.2.3 Heap upward adjustment algorithm
The upward adjustment algorithm is generally used when inserting data into the heap, and can also be used directly to build a heap. Now we are given an array, which is logically viewed as a complete binary tree. We can adjust it into a small heap through the upward adjustment algorithm starting from the insertion point. The upward adjustment algorithm of the heap refers to adjusting a node upward so that it meets the properties of the heap. The upward adjustment algorithm of the heap is as follows:
1. Starting from the last non-leaf node, adjust each node upward in sequence.
2. Compare the current node with its parent node. If the value of the current node is greater than the value of the parent node, exchange the values of the two nodes.
3. Repeat step 2 until the current node reaches the root node.
Look at the code:
void Swap(HPDataType* p1, HPDataType* p2) { HPDataType tmp = *p1; *p1 = *p2; *p2 = tmp; } void AdjustUp(HPDataType* a, int child) { int parent = (child - 1) / 2; while (child > 0) { if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); child = parent; parent = (child - 1) / 2; } else { break; } } }There are several details that need to be paid attention to when writing this algorithm:
1. How to find parent nodes.
2. Conditions of exchange.
3. Conditions for ending the exchange
1. Let’s take 1 (parent node), 3 and 4 (child node) as an example.
To find the parent node, we only need int parent = (child - 1) / 2. If the left child 3 is brought in, the result will be true; if the right child 4 is brought in, the result will also be true.
2. If you want to create a large heap, then the child node must be larger than the parent node before exchanging; if you want to create a small heap, then the child node must be smaller than the parent node before exchanging.
3. End the exchange and the child reaches the 0 node, which means it is over.
3.2.4 Use the downward adjustment algorithm to build a large heap
When you can also build a small heap, of course you can also use the upward adjustment algorithm to build a heap. It is worth mentioning here that the time complex heap using the downward adjustment algorithm is better than the upward adjustment algorithm.
int a[] = {1,5,3,8,7,6};
See code:
#include<stdio.h> #include<stdlib.h> typedef int HPDataType; void Swap(HPDataType* p1, HPDataType* p2) { HPDataType tmp = *p1; *p1 = *p2; *p2 = tmp; } void AdjustDown(int* a, int size, int parent) { int child = parent * 2 + 1; while (child < size) { if (child + 1 < size && a[child + 1] > a[child]) { ++child; } if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } else { break; } } } void HeapSort(int* a, int n) { //建大堆 for (int i = (n - 1 - 1) / 2; i >= 0; --i) { AdjustDown(a, n, i); } } int main() { int a[] = { 1,5,3,8,7,6 }; HeapSort(a, sizeof(a)/sizeof(int)); for (int i = 0; i < sizeof(a)/sizeof(int); i++) { printf("%d ", a[i]); } printf("\n"); return 0; }
3.2.4.1 The time complexity of using downward adjustment algorithm: O(N).
3.2.4.2 Time complexity of using upward adjustment algorithm: O(NlogN)
3.2.5 Insert node
We know the two insertion algorithms, upward and downward, and inserting nodes is very easy. The first thing to consider is the capacity issue. If the capacity is insufficient, it needs to be expanded. Then insert the data. Finally, use algorithm adjustment.
void HeapPush(HP* php, HPDataType x) { assert(php); if (php->size == php->capacity) { int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2; HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType)); if (tmp == NULL) { perror("realloc fail"); exit(-1); } php->a = tmp; php->capacity = newCapacity; } php->a[php->size] = x; php->size++; AdjustUp(php->a, php->size - 1); }
3.2.6 Delete node
Generally speaking, when deleting a heap node, you delete the root node of the heap. When we delete the root node, we cannot delete the root node directly. If the root node is deleted, the entire structure of the heap will be messed up. We can first exchange the root node and the tail node, then --size will have the effect of deletion, and finally use the downward adjustment algorithm to adjust the heap.
void HeapPop(HP* php) { assert(php); assert(php->size > 0); Swap(&php->a[0], &php->a[php->size - 1]); php->size--; AdjustDown(php->a, php->size, 0); }
3.4 Application of heap
Taking a large heap as an example, we can know from its structure that if we want to get the maximum value of the data in the heap, we only need to get the root node. If we want to get the second largest value, we delete the root node. The adjusted root node is the second largest value. We found that we can use the heap to get ordered data, which led us to heap sorting and using heaps to solve the TOP-K problem.
3.4.1 Heap sort
Heap sorting uses the idea of a heap to sort. It is divided into two steps:
1. Build a heap
Ascending order: build a large heap
Descending order: Build a small heap
2. Use the idea of heap deletion to sort1. Construct the data to be sorted into a max heap.
2. Exchange the top element (maximum element) with the last element and reduce the size of the heap.
3. Pack the previous N -1 element to make it the largest pile.
4. Repeat steps 2 and 3 until there is only one element left in the heap.
See code:
#include<stdio.h> #include<stdlib.h> typedef int HPDataType; void Swap(HPDataType* p1, HPDataType* p2) { HPDataType tmp = *p1; *p1 = *p2; *p2 = tmp; } void AdjustDown(int* a, int size, int parent) { int child = parent * 2 + 1; while (child < size) { if (child + 1 < size && a[child + 1] > a[child]) { ++child; } if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } else { break; } } } // 升序 void HeapSort(int* a, int n) { for (int i = (n - 1 - 1) / 2; i >= 0; --i) { AdjustDown(a, n, i); } int end = n - 1; while (end > 0) { Swap(&a[0], &a[end]); AdjustDown(a, end, 0); --end; } } int main() { int a[] = { 4, 6, 2, 1, 5, 8, 2, 9 }; HeapSort(a, sizeof(a)/sizeof(int)); for (int i = 0; i < sizeof(a)/sizeof(int); i++) { printf("%d ", a[i]); } printf("\n"); return 0; }
3.4.2 Use heap to solve TOP-K problem
TOP-K problem: Find the top K largest elements or smallest elements in data combination. Generally, the amount of data is relatively large.
For example: top 10 professionals, Fortune 500, rich list, top 100 active players in the game, etc.
For the Top-K problem, the simplest and most direct way that can be thought of is sorting. However: if the amount of data is very large, sorting is not advisable (maybe the data cannot be loaded all at once. in memory).The best way is to use a heap to solve the problem. The basic idea is as follows:
1. Use the first K elements in the data set to build a heap
For the top k largest elements, build a small heap
For the top k smallest elements, build a large heap
2. Use the remaining N-K elements in sequence with The top element of the heap is compared, and if it is not satisfied, the top element of the heap is replacedAfter comparing the remaining N-K elements with the elements at the top of the heap, the remaining K elements in the heap are the required first K smallest or largest elements.
eg: Select the five largest data from one million data
#define _CRT_SECURE_NO_WARNINGS 1 #include<stdio.h> #include<stdlib.h> #include<assert.h> #include<stdbool.h> #include<time.h> typedef int HPDataType; void Swap(HPDataType* p1, HPDataType* p2) { HPDataType tmp = *p1; *p1 = *p2; *p2 = tmp; } void AdjustUp(HPDataType* a, int child) { int parent = (child - 1) / 2; while (child > 0) { if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); child = parent; parent = (child - 1) / 2; } else { break; } } } void AdjustDown(HPDataType* a, int size, int parent) { int child = parent * 2 + 1; while (child < size) { if (child + 1 < size && a[child + 1] < a[child]) { ++child; } if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } else { break; } } } void CreateNDate() { // 造数据 int n = 10000000; srand(time(0)); const char* file = "data.txt"; FILE* fin = fopen(file, "w"); if (fin == NULL) { perror("fopen error"); return; } for (int i = 0; i < n; ++i) { int x = (rand() + i) % 10000000; fprintf(fin, "%d\n", x); } fclose(fin); } void PrintTopK(const char* file, int k) { FILE* fout = fopen(file, "r"); if (fout == NULL) { perror("fopen error"); return; } // 建一个k个数小堆 int* minheap = (int*)malloc(sizeof(int) * k); if (minheap == NULL) { perror("malloc error"); return; } // 读取前k个,建小堆 for (int i = 0; i < k; i++) { fscanf(fout, "%d", &minheap[i]); AdjustUp(minheap, i); } int x = 0; while (fscanf(fout, "%d", &x) != EOF) { if (x > minheap[0]) { minheap[0] = x; AdjustDown(minheap, k, 0); } } for (int i = 0; i < k; i++) { printf("%d ", minheap[i]); } printf("\n"); free(minheap); fclose(fout); } int main() { CreateNDate(); PrintTopK("data.txt", 5); }
The results are as above. If you want to see the values of the first k numbers more intuitively, you can modify the numbers in the file you created. Just modify 5 numbers larger than one million.
Hope this article helps you! ! !