[Dynamic Programming] Solve the edit distance problem

Problem Description
recurrence relationship
Running instance
Time and space complexity optimization
Hirschberg algorithm

Problem Description

The edit distance problem is to solve the insertion, deletion, and replacement required to convert one string to another string. Minimum number of times. $\mathbb{COMMOM} \overset{sub}{\rightarrow} \mathbb{COMMUM} \overset{sub}{\rightarrow}\mathbb{ COMMUN} \overset{ins}{\rightarrow} \mathbb{COMMUNE}$ A total of at least 3 operations are required to change the word COMMOM into COMMUNE.

Visualize edit distances to obtain sequence alignments

C	O	M	M	O	M	-
C	O	M	M	IN	N	AND

A space in the first line indicates insertion
A space in the second line indicates deletion
Columns with different characters represent substitutions

Edit distance = the number of columns with different characters in the sequence alignment

Minimum edit distance = the number of columns with different characters in the optimal sequence alignment

The edit distance problem can also be expressed like this:
For a given string $A [1... m]$ Sum $B [1... n]$ Solution other minimum distance $D (m, n)$

recurrence relationship

假设对 $\forall i<m,\forall j<n$ , possible calculation $A [1... i]$ 和 $B [1... j]$ 's minimum distance $D (i, j)$ 。

C	O	M	M	O	M	-
C	O	M	M	IN	N	AND

Thoughts $A [1... m]$ Sum $B [1... n]$ The most preferable ratio, the rules below are as follows:

The last column cannot be two spaces
When a string is an empty string, the minimum edit distance is the length of another string
$A [m]$ Sum $B [n]$ 都是： $D (m, n) = D (m - 1, n - 1) + (A [m] = B [n]? 0 : 1)$
$A [m]$ Sum $B [n]$ One side is empty, Delete the one that is not empty: $\begin{cases} D(m − 1,n) + 1 & A[m]\quad and \quad- \\ D(m, n − 1 ) + 1 & B[n]\quad and \quad- \\ \end{cases}$
To sum up, you only need to recurse along the three paths to get the smallest one $\begin{cases} i &if\quad j=0\\ j &if\quad i=0 \\ \min \begin{cases} D(m − 1,n) + 1 \\ D(m, n − 1) + 1 \\ D(m − 1,n − 1) + (A[m] = B[n]?0 : 1) \end{cases} &otherwise \end{cases}$
Time efficiency： $O (mn)$ ; Space power: $O (mn)$ 。

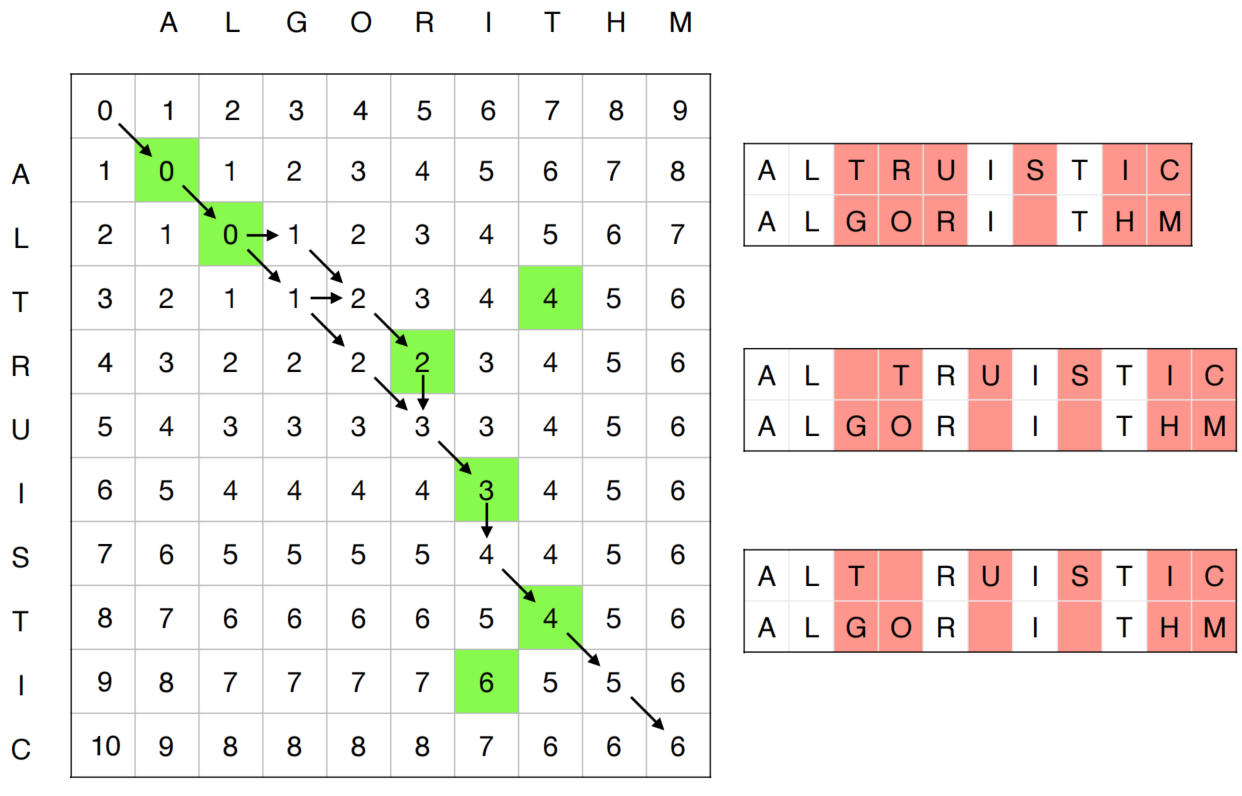
Running instance

Insert image description here
对于每个 $D [i, j]$ , 都可以通过 $D [i - 1, j - 1]$ ; $D [i - 1, j]$ ; $D [i, j - 1]$ These three points are obtained, and these three points respectively correspond to three operations: replacement; deletion; insertion.

Through the above recursion relationship, we can construct the record table from top to bottom and from left to right. After filling in the record form, the value in the lower right corner is the minimum editing distance. The next step is to use backtracking to construct the optimal alignment that satisfies the minimum edit distance (as shown on the right side of the figure below)
Insert image description here

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>

using namespace std;

// 计算最小编辑距离，并返回最小编辑距离的值，计算编辑距离表dp
int minEditDistance(const string& word1, const string& word2, vector<vector<int>>& dp) {
    
    
    int m = word1.length();
    int n = word2.length();

    for (int i = 0; i <= m; ++i) {
    
    
        for (int j = 0; j <= n; ++j) {
    
    
            if (i == 0) {
    
    
                dp[i][j] = j;
            }
            else if (j == 0) {
    
    
                dp[i][j] = i;
            }
            else if (word1[i - 1] == word2[j - 1]) {
    
    
                dp[i][j] = dp[i - 1][j - 1];
            }
            else {
    
    
                dp[i][j] = 1 + min({
    
     dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1] });
            }
        }
    }

    return dp[m][n];
}

// 通过回溯法找到所有满足最小编辑距离的操作序列。
void findAllSequences(const string& word1, const string& word2, int i, int j, const string& sequence, vector<string>& sequences, vector<vector<int>>& dp) {
    
    
    if (i == 0 && j == 0) {
    
    
        sequences.push_back(sequence);
        return;
    }

    if (i > 0 && j > 0 && word1[i - 1] == word2[j - 1]) {
    
    
        findAllSequences(word1, word2, i - 1, j - 1, "No operation: " + string(1, word1[i - 1]) + " -> " + string(1, word2[j - 1]) + "\n" + sequence, sequences, dp);
    }

    if (i > 0 && j > 0 && dp[i][j] == dp[i - 1][j - 1] + 1) {
    
    
        findAllSequences(word1, word2, i - 1, j - 1, "Replace: " + string(1, word1[i - 1]) + " -> " + string(1, word2[j - 1]) + "\n" + sequence, sequences, dp);
    }

    if (i > 0 && dp[i][j] == dp[i - 1][j] + 1) {
    
    
        findAllSequences(word1, word2, i - 1, j, "Delete: " + string(1, word1[i - 1]) + " \n" + sequence, sequences, dp);
    }

    if (j > 0 && dp[i][j] == dp[i][j - 1] + 1) {
    
    
        findAllSequences(word1, word2, i, j - 1, "Insert: " + string(1, word2[j - 1]) + " \n" + sequence, sequences, dp);
    }
}

int main() {
    
    
    string word1 = "ALTRUISTIC";
    string word2 = "ALGORITHM";

    vector<vector<int>> dp(word1.length() + 1, vector<int>(word2.length() + 1, 0));

    int minDistance = minEditDistance(word1, word2, dp);

    cout << "Minimum Edit Distance between " << word1 << " and " << word2 << " is: " << minDistance << endl;

    vector<string> sequences;
    findAllSequences(word1, word2, word1.length(), word2.length(), "", sequences, dp);

    cout << "Operations to convert " << word1 << " to " << word2 << " are: " << endl;
    for (const string& seq : sequences) {
    
    
        cout << seq << "----------"<< endl;
    }

    return 0;
}

operation result:

Insert image description here

Time and space complexity optimization

Now we can calculate the minimum edit distance and construct the optimal alignment. Their space-time complexity is summarized as follows:

	Calculate minimum edit distance	Construct optimal alignment
time	$O (mn)$	$O (m + n)$
space	$O (mn)$	$O (mn)$

From the actual situation, $O (mn)$ space ratio $O (mn)$ , comparison $m = n = 10^5$ time

Time: Execution $10^{10}$ instructions take about 10 seconds (assuming the CPU executes $10^9$ Article Directive)
Spatially: required $10^{10}$ bits, approx. 40 GB

な么ability用 $O (m + How to construct the optimal alignment in the space of n)$ ?

Answer: Hirschberg algorithm can be used.

Hirschberg algorithm

The Hirschberg algorithm is an efficient linear space dynamic programming algorithm. It reduces space complexity by using a divide-and-conquer strategy to compute optimal alignments in linear space.

The idea of this algorithm is based on the following insights:

In dynamic programming algorithms, two-dimensional matrices are usually used to store intermediate states, which results in $O (mn)$ の空间复杂degree.
But in fact, by observing the symmetry in the calculation process, the space complexity of dynamic programming can be reduced to $O (m + n)$ 。

Insert image description here
During the calculation of dynamic programming, we observed that $D (i,$ $D (i - 1, j)$ 、 $D (i, j - 1)$ 和 $D (i - 1, j - 1)$ . Based on this, we can use two one-dimensional arrays of length n to store the intermediate state, and only need to retain the information of the previous row and the current row each time.