498. Diagonal traversal
-
To simplify the problem, first consider printing elements diagonally one by one, without considering flipping.
-
A two-dimensional matrix with M rows and N columns has a total of M + N - 1 diagonal lines ( upper right -> lower left )
-
1) How to traverse: Traverse the number of diagonals from left to right , traversing M + N - 1 rounds in total, d: [0, M + N - 1 ) Determine the upper right corner of the current diagonal d in each round The coordinates (x, y) of the point , then use this point as the starting point, start a while loop, and follow the x++, y-- method, that is, the upper right -> lower left direction, traverse the matrix located on the diagonal point, and save it to the result array res[i++] = matrix[x][y] , the judgment condition of the while loop: x < M && y >= 0 , that is, if neither of them crosses the boundary, it will continue to loop until it crosses the boundary.
-
2) How to save the polyline: When d%2 == 0, you need to save it in reverse, so you can make a list at this time , and then save it with Collections.reverse(list) , or start the inner while loop of traversing the diagonal every time Write down the current position of the res array as start . At the end of the while loop, the i subscript of res is the end position. Just reverse the interval of res[start...i] (you can write a function to reverse the array interval here).
-
3) How to determine the coordinates of the upper-right corner point of diagonal line d : In fact, the upper-right corner points of all diagonal lines are those points located in the top row and right-most column of the entire matrix, so when d < N , so The x- coordinates of the points sought are all 0 , and the y -coordinates are d , that is, [ 0, d] . When d >= N , the x- coordinates of the points sought are d - ( N - 1 ) , and the y -coordinates are all is N - 1 , that is [ d - ( N - 1 ) , N - 1] .
As shown below:
The biggest difficulty in this question is to first observe that the number of right diagonals of a two-dimensional matrix is M + N - 1 , because this is the number of rounds of diagonals we want to traverse. Secondly, we need to determine the coordinates (x, y) of the upper right corner of each diagonal line and calculate it equivalently using the diagonal subscript. (Why, because we are traversing the diagonal, we cannot get the two-dimensional coordinates of each point at this time, so we need to convert)
In order to see it more clearly, we remove all the numbers in the matrix:
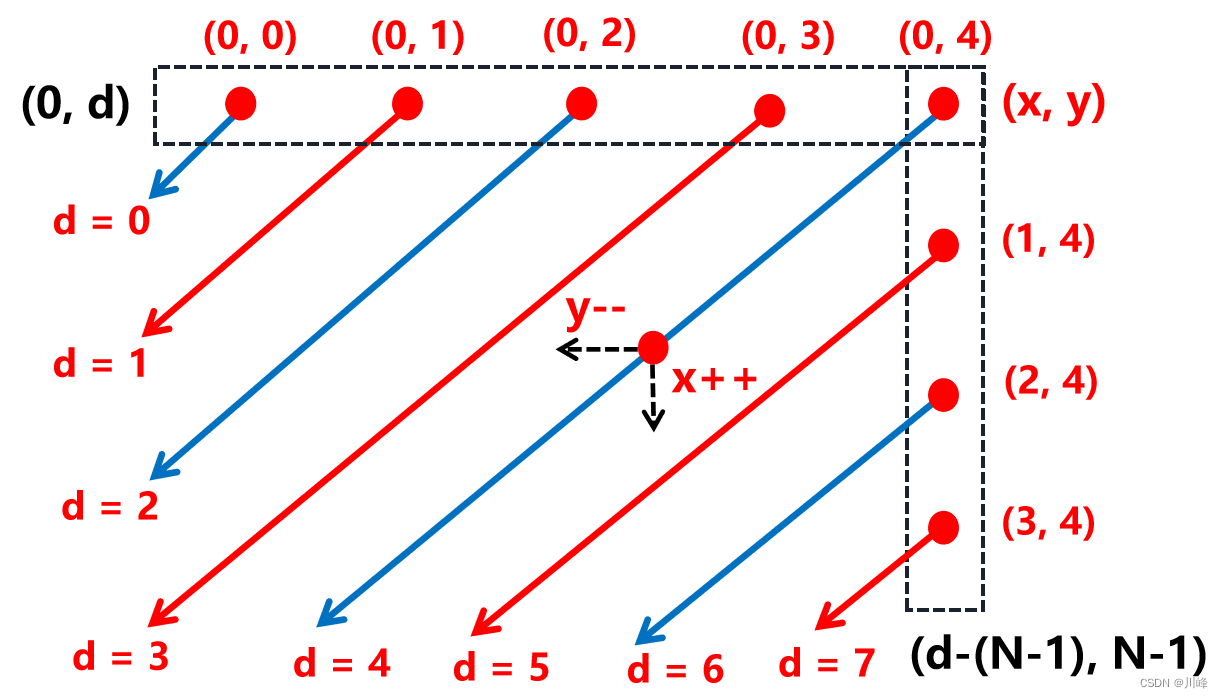
In fact, the coordinates of the diagonal starting point of the top row are the coordinate points of the first row of the two-dimensional matrix. Their abscissas are all 0 , and the ordinate is the column subscript of the two-dimensional matrix for that point, which can be considered as ( 0, j) , but when we traverse, we traverse the number of diagonal rounds [0, M + N - 1] , rather than traversing the two-dimensional matrix like the general double for loop (if that is the case, can get i and j ), so the coordinates of the diagonal starting point of the first row need to be equivalently calculated using the round number subscript of the diagonal, which is exactly (0, d) .
Similarly, the starting point of the diagonal of the last column is actually the coordinate point (i, N - 1) of the last column of the two-dimensional matrix . We also need to use the subscript of the diagonal to calculate it equivalently, which is (d - (N - 1), N - 1) .
Finally, when saving the answer, you need to use a little trick, that is, the value on the odd-numbered diagonal (or the diagonal subscript is d=0, 2, 4... ), Just save it in reverse order. That is, the blue diagonal line in the picture above should look like this:
54. Spiral matrix
-
1) Access by layer/ring : cyclic access to the four edges of the upper, right, lower and left edges. Let 4 variables represent the upper, lower, left and right boundaries respectively: T = 0, B = M - 1, L = 0, R = N - 1 ,
-
First, use a while loop in the outermost layer to control the four directions without crossing the boundary: T < B && L < R ,
-
Then in each loop, use 4 for loops to collect the values on the four edges of the upper, lower, left and right sides respectively. After the collection, the four edges shrink inward by one circle at the same time T++ B-- L++ R-- ,
-
When finally jumping out of the while loop, there will be only one row T==B or one column L==R left , just collect them.
As shown below:
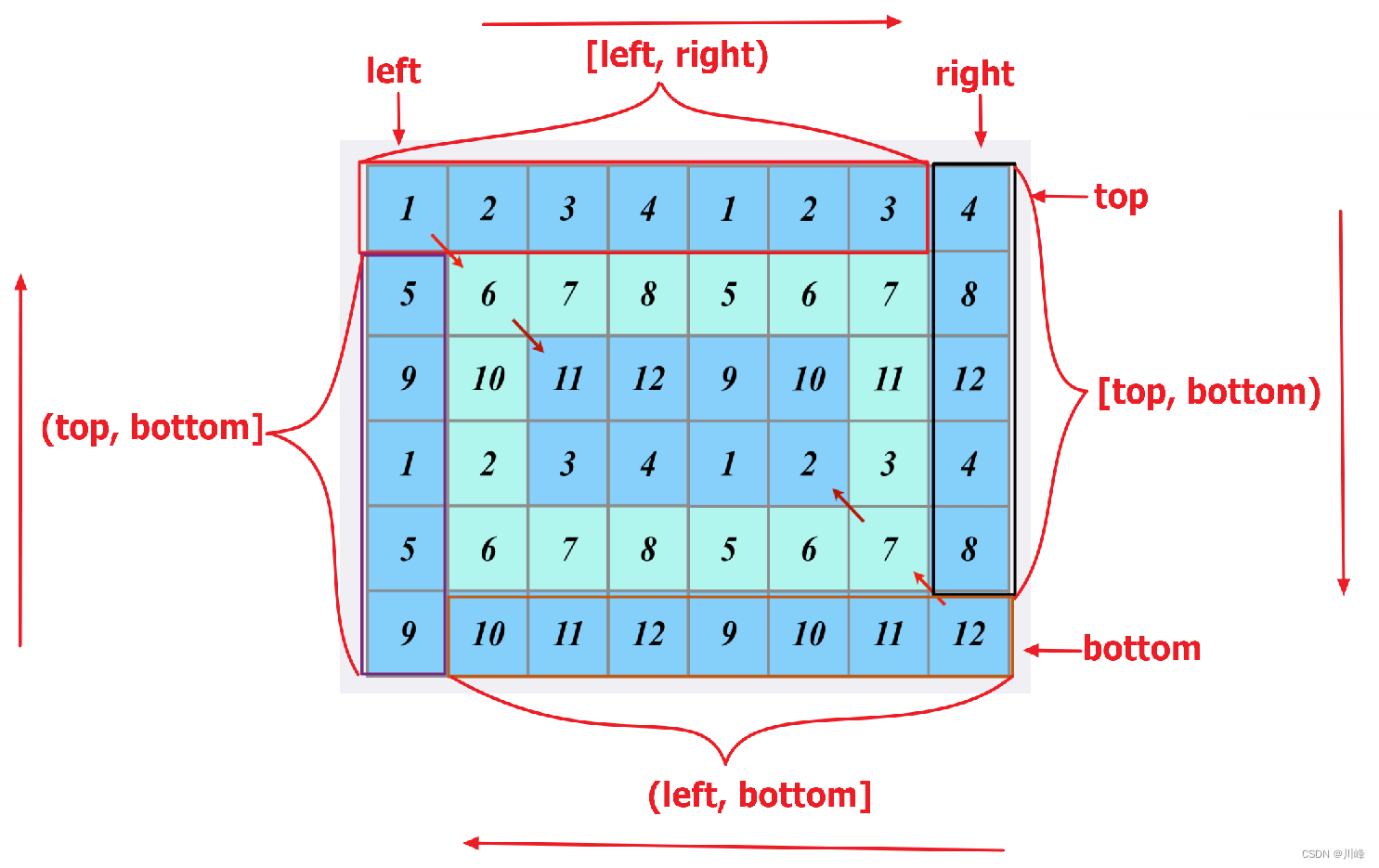
For example, when collecting the above row, use a for loop to traverse the interval i: [L, R) . At this time, the abscissa is fixed at T , and the traversal subscript is the column coordinate, so the value of each element in the for loop is matrix[ T][i] . Similarly, for the collection i on the right: [T, B) , the value of the element is matrix[i][R] ; for the collection i: [R, L) below , the value of the element is matrix[B][ i] ; for the left collection i: [B, T) , the value of the element is matrix[i][L] .
When it finally shrinks to the innermost layer, only one row or column will remain, as shown in the following figure:
One thing to note in the above code is that when there is only one row or column left, it can only be written in the form of if...else if... , and cannot be written in the form of two ifs judged side by side. Because for a square matrix like the question example 1, there will only be one point left in the end. At this time, T==B or L==R will be satisfied at the same time. If it is written in the form of two ifs judged side by side, this point will be collected one more time. , leading to wrong answers.
-
2) DFS traversal: Starting from (0,0) , press DFS in the four directions of right, bottom, left, and top, and define a two-dimensional direction array int [][] dirs = { { 0 , 1 }, {1, 0} , {0, -1}, {-1, 0} } , and the boolean[][] visited array, collect the current node each time and mark it as visited , and then calculate the next node x + dirs[k][0], y + dirs[k][1] , where k represents the direction, and the initial k == 0. After collecting the nodes in each recursion, first determine whether the next point is out of bounds or has been visited . If it is not out of bounds and has not been visited, then Make a recursive call, and if it goes out of bounds or has been visited, change the direction k = ( k + 1 ) % 4 , and then recalculate the value of the next node again (note).
-
It can be implemented using loops (looping MXN times) or dfs recursive function standard templates.
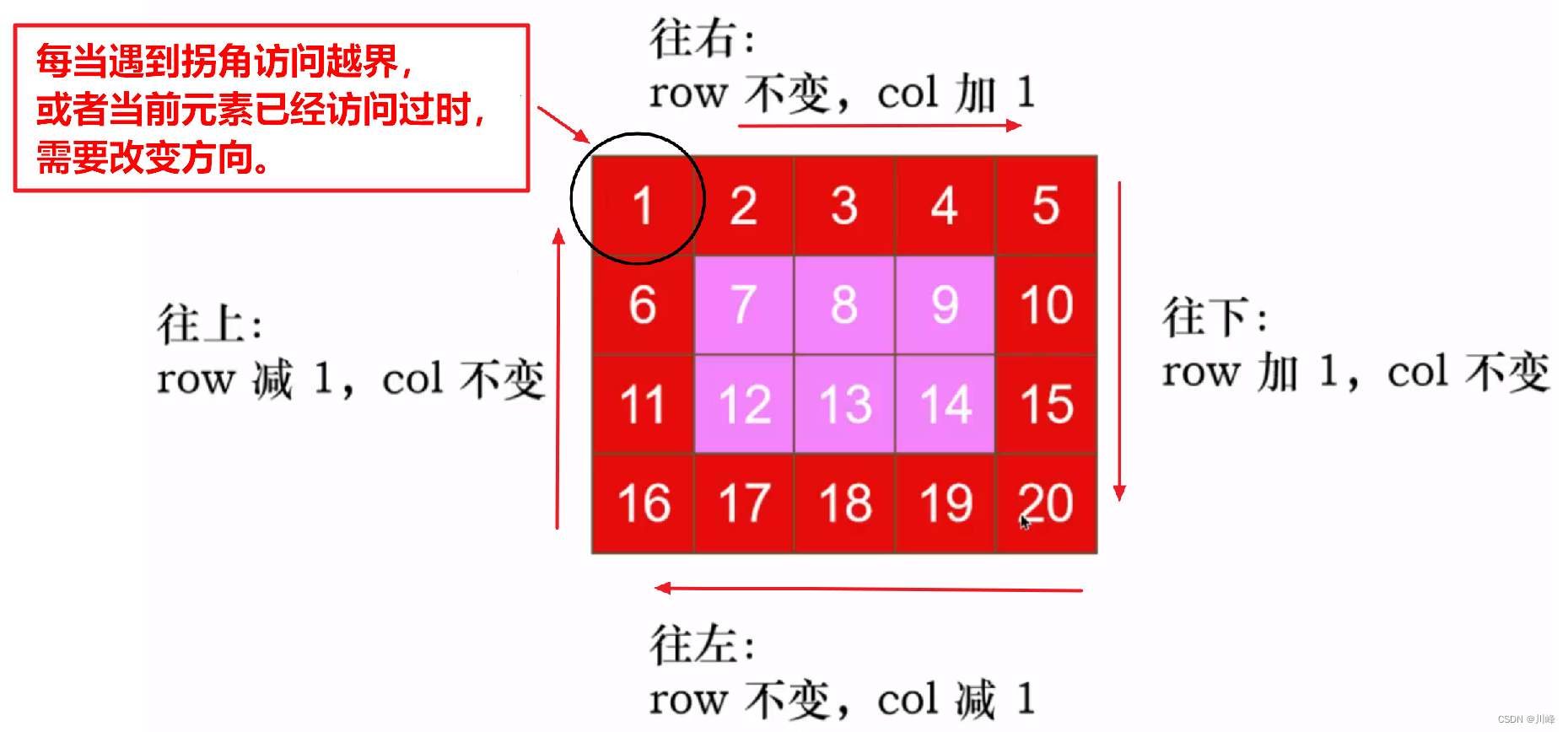
Recursive version:
Iterative version:
59. Spiral Matrix II
-
Same as 54, first create a two-dimensional array, and replace the place where you get the matrix[x][y] value in question 54 with assigning a value to matrix[x][y] .
DFS recursive version:
DFS iteration version:
73.Matrix zeroing
-
1) Use two boolean arrays rows[M] and cols[N] to record whether each row and each column needs to be set to 0 ,
-
First traverse the matrix. If matrix[i][j] == 0 , record rows[i] = true and cols[j] = true .
-
Finally, iterate through the matrix again . If rows[i] or cols[j] is true , set matrix[i][j] to 0 .
-
The space complexity of this method is O(m+n)
-
2) Use the 0th row and 0th column of the original matrix as two marker arrays to record whether a row or column other than the first row and column needs to be set to 0.
-
Two variables need to be used in advance to mark whether row 0 and column 0 contain 0 ,
-
Then traverse the matrix first and start processing from the [1,1] position. If matrix[i][j] == 0 , update matrix[i][0] == 0 (this row needs to be set to 0) and matrix[ 0][j] == 0 (this column needs to be set to 0) ,
-
Then traverse the matrix again , start processing from the [1,1] position, and determine if matrix[i][0] == 0 or matrix[0][j] == 0 , then set matrix[i][j] 0 .
-
After the final processing is completed, whether row 0 and column 0 need to be set to 0 will be processed based on the first two mark variables alone .
-
3) Optimization for method 2: still use the 0th row and 0th column of the original matrix , and then use only one variable to mark whether the 0th column needs to be set to 0 , and traverse everything except the 0th column starting from the last row in reverse order Each element is processed in parallel, thus preventing the element in row 0 from being updated early (row 0 will be processed last). This method just saves one variable.
The key point of this question is that you cannot set the previous position to 0 first, because the behavior of "setting all the rows and columns to 0" will affect the judgment of the subsequent position. If a certain position in the latter position is due to the previous The position judgment processing is set to 0 in advance, and when used later, it will be the value after being overwritten. In this way, accurate judgment cannot be made later, and it is very likely that the matrix will be set to 0. Therefore, we need to find an additional place to record the mark "whether a certain row or column needs to be set to 0". The simple idea is that method 1 uses two additional arrays to record (space O(m+n)), and saves space more efficiently. The idea is to use part of the original matrix to record, that is, method 2 and method 3 (space O(1)).
289.Game of Life
-
Since the value of each element in the matrix is only 0 or 1 , the binary bit of each element in the matrix can be used to represent the composite state ,
-
Use the lower 2 bits 00 of the 32-bit integer , where the lower bits are used to represent the original state and the higher bits are used to represent the modified state .
-
Traverse the matrix , find the number of living cells in the eight directions around each position (using the dirs array technique), and then modify the value of the high-order bits of the lower 2 binary bits of each element according to the rules of the question .
-
If you need to change a dead cell to a live cell , you only need to perform the num | 10 operation to set the high position to 1. If you need to change a living cell to a dead cell, the high position does not need to be moved ( because the original value is only 0 or 1, Only the low bits are used, so the high bits default to 0, 01 or 00 ).
-
Note: The element value is used directly when judging the original state, because each element of the traversed matrix is accessed for the first time and has not been modified, and modification is to modify the high-order bits of the element 's binary bits. However, when calculating the number of living cells in the eight directions around the current element , you should use num & 1 to judge, that is, only look at the original state of its low bits , because the elements in the eight directions may have been modified.
-
Finally, traverse the matrix again and change each element into the value of the high -order bits of its low-order two binary bits (through the >>1 operation ).
This question is very similar in thought to question 73, that is, you need to find a place to store the modified state value first, and then modify the matrix according to the stored state mark. However, the question requires modification in place, so you can only modify it in the original matrix. This question uses the free binary bits of the element value (the question elements are only 1 or 0).
48. Rotate images
-
1) The same idea as the 54 spiral matrix, accessed by layer/ring/circle , defining four direction boundaries T = 0, B = N - 1, L = 0, R = N - 1 ,
-
The condition of the outer loop is L < R (or T < B ). In each loop, the element values located on the four edges are exchanged respectively. The number of exchanges controlled by the loop is R - L or B - T , and the exchange is completed. Finally, the outer layer shrinks inward, namely T++, B--, L++, R-- .
-
Note: When exchanging elements, do so in a clockwise direction (you must first reserve pits in order and proceed backwards)
-
The top element value should be placed on the rightmost matrix[T][L+i] -> matrix[T+i][R] ,
-
The rightmost element value should be placed at the bottom matrix[T+i][R] -> matrix[B][Ri] ,
-
The bottom element value should be placed on the leftmost matrix[B][Ri] -> matrix[Bi][L] ,
-
The leftmost element value should be placed at the top matrix[Bi][L] -> matrix[T][L+i]
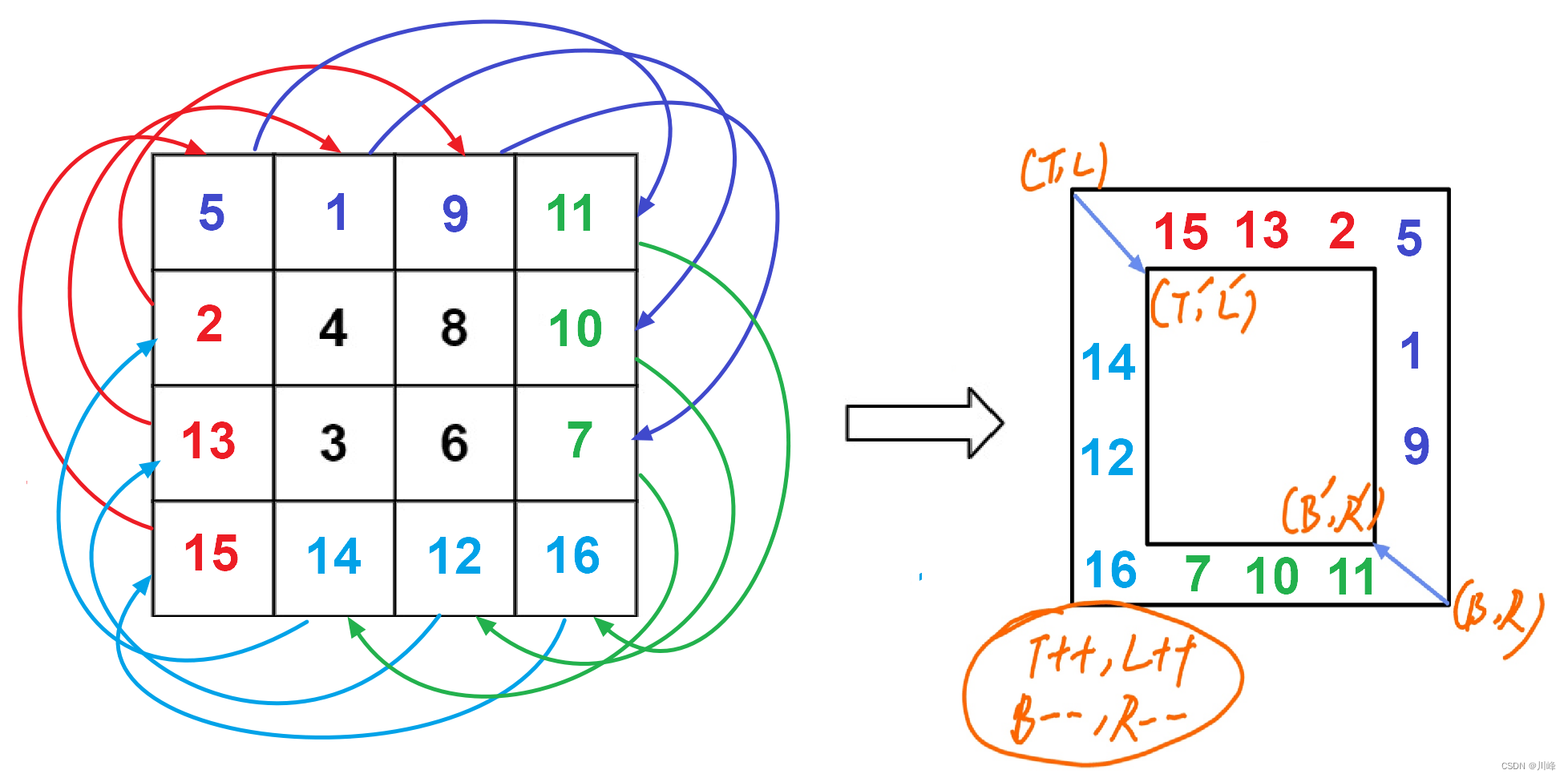
As shown in the figure above, although the exchange effect is clockwise, when actually exchanging codes, you need to remember one side first, leave a pit, and then fill the pit in a counter-clockwise order.
Note that in the above code, the exit condition of the while loop is L < R , but compared with question 54, there is no need to deal with the situation of L==R (or T==B ). This is because the input of this question is an nxn square . Matrix, the characteristics of this matrix are:
- 1) Either L==R exits in the end. At this time, there is still one point left in the middle. Naturally, there is no need to continue the exchange. For example, this is the case for a 3x3 matrix.
- 2) Either L > R exits at the end. At this time, all the exchanges in the matrix have been completed and there is nothing left. For example, this is the case for a 4x4 matrix.
-
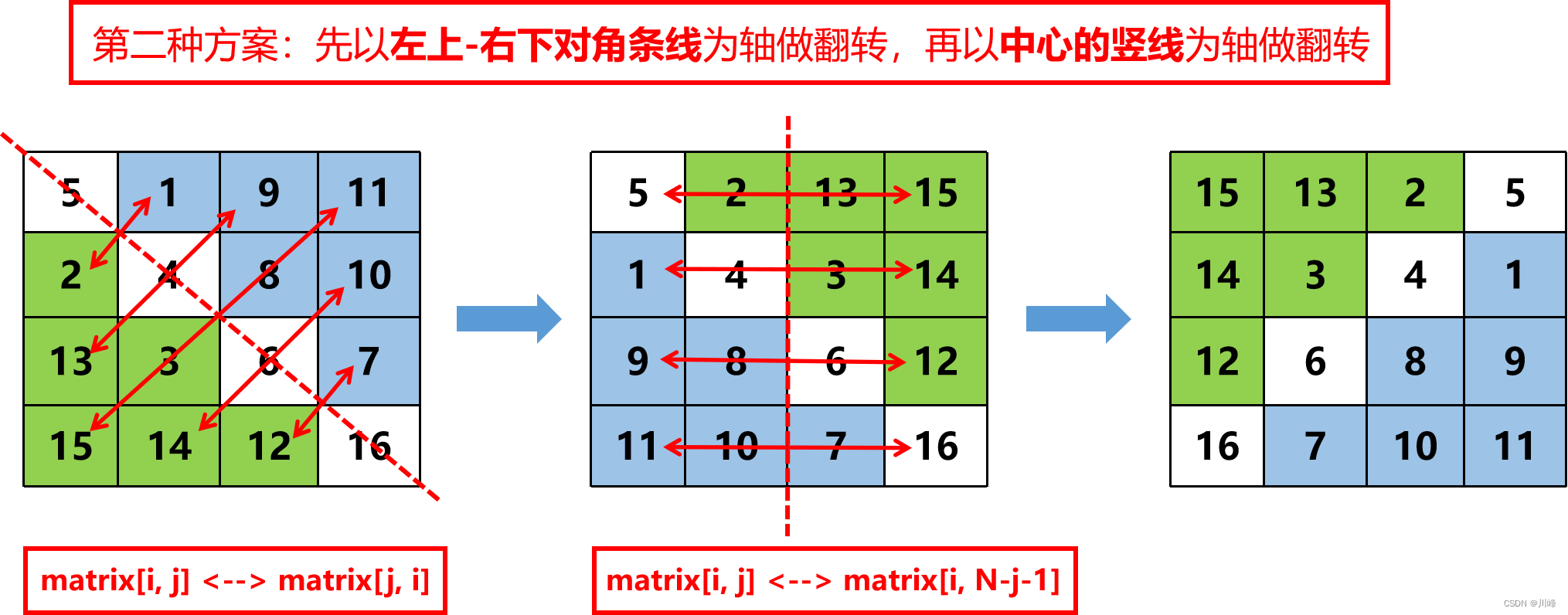
2) First mirror and flip along the left diagonal , then mirror and flip left and right along the vertical line of the central axis .
-
The specific operation of diagonal mirror flipping: traverse the lower left half of the matrix i: [0, N), j: [0, i) , and exchange matrix[i, j] and matrix[j, i] .
-
The specific operation of left and right mirror flipping: traverse the left half of the matrix i: [0, N), j: [0, N / 2) , exchange matrix[i , j] and matrix[i , N - j - 1] , that is Can.
-
3) First mirror up and down along the horizontal line of the central axis , and then mirror along the left diagonal .
-
The specific operation of mirror flipping up and down: traverse the upper half of the matrix i: [0, N / 2), j: [0, N) , exchange matrix[i, j] and matrix[N - i - 1, j] , that is Can.
-
The specific operation of diagonal mirror flipping: traverse the lower left half of the matrix i: [0, N), j: [0, i) , and exchange matrix[i, j] and matrix[j, i] .
This question can actually be done by flipping left and right mirror images + flipping right diagonal mirror images , or flipping right diagonal mirror images + flipping up and down mirror images. You can find out through observation. But the coordinates of the right diagonal are not as convenient as the left diagonal when exchanging.
118.Yang Hui Triangle
-
Convert the problem into a left-aligned two-dimensional array to think about. The current value = the value of the previous row + the value of the upper left
-
In the i -th row, the 0th and last columns are 1 , and the others satisfy res[i][j] = res[i - 1][j] + res[i - 1][j - 1 ]
-
Process it by traversing the two-layer for loop of the matrix. The number of rows of the matrix is N given in the question , and the number of columns of the matrix : the i-th row has i + 1 columns , so j: [0, i] (i starts from 0)
If you find List troublesome, you can directly use a two-dimensional array to calculate, and then transfer it again, but it is also troublesome:
119.Yang Hui Triangle II
-
1) Same as 118, first generate the Yang Hui triangle array with rowIndex + 1 row, and then return to rowIndex row
Problem-solving ideas:
-
2) Use a rolling array to remember the previous row. After each update of the current row, assign the current row to the previous row.
-
3) Use an array, update from right to left in each row, and calculate in reverse order starting from the j = i column, res[j] = res[j] + res[j - 1], initial res[0] = 1
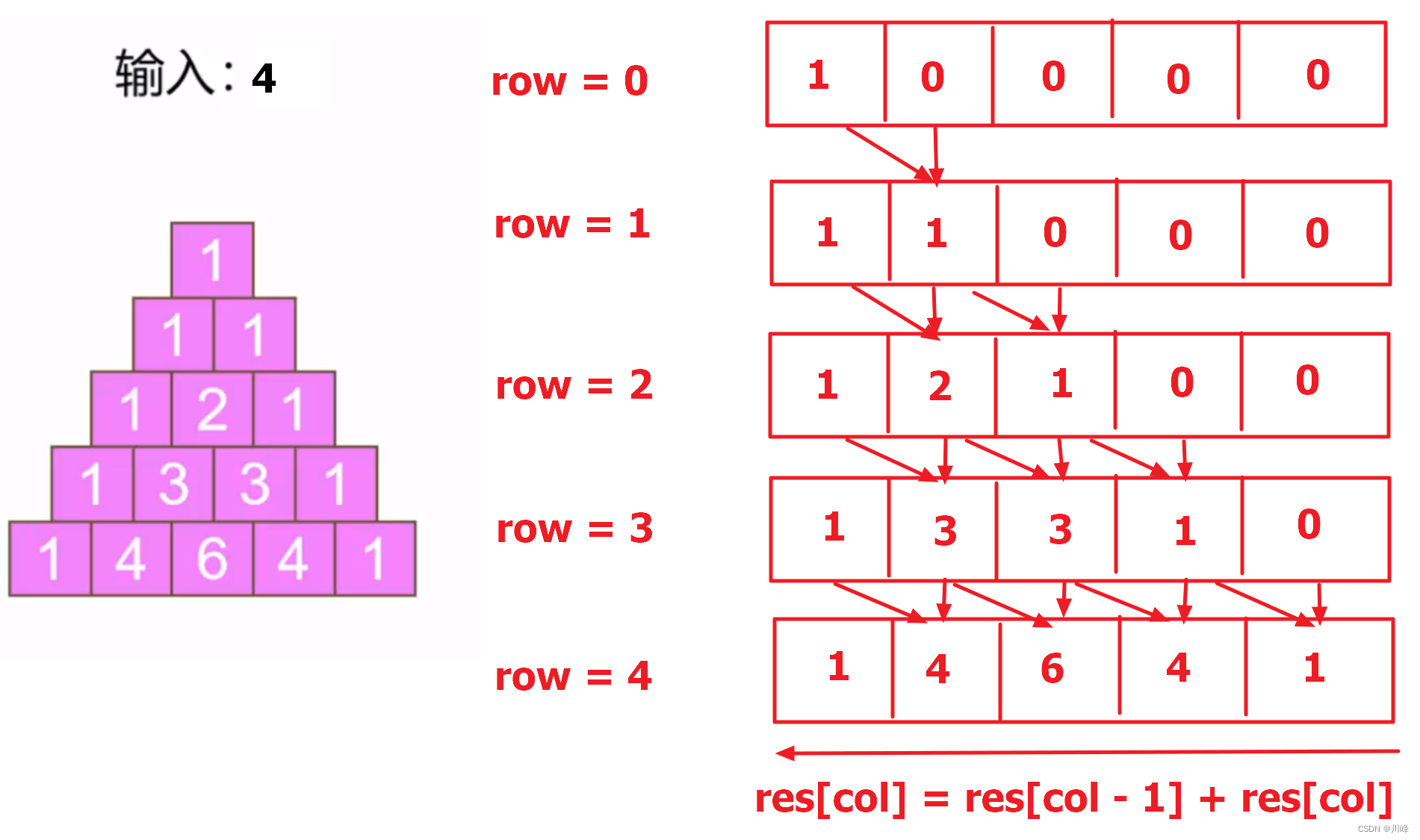
At this time, when the current row has not been updated, the array itself is regarded as the value left from the previous row. The value at the current position is actually the value in the row above the current position, and the value at the previous position is actually the value before the previous row. The value of the location.
36. Effective Sudoku
-
Use 3 boolean marker arrays to mark whether 1-9 appears in each row, each column, and each 3x3 grid of the original array.
- Scan each number in the two-dimensional array to determine whether it has appeared in these 3 mark arrays. If it has appeared, it violates the rules of Sudoku and returns false ; if it has not appeared, put it in these 3 Each tag array is marked as true .
- Note: When traversing the matrix, spaces (i.e. characters ' . ') are skipped and only numeric characters are processed.
For each row of numbers 1-9, the definition is as follows:
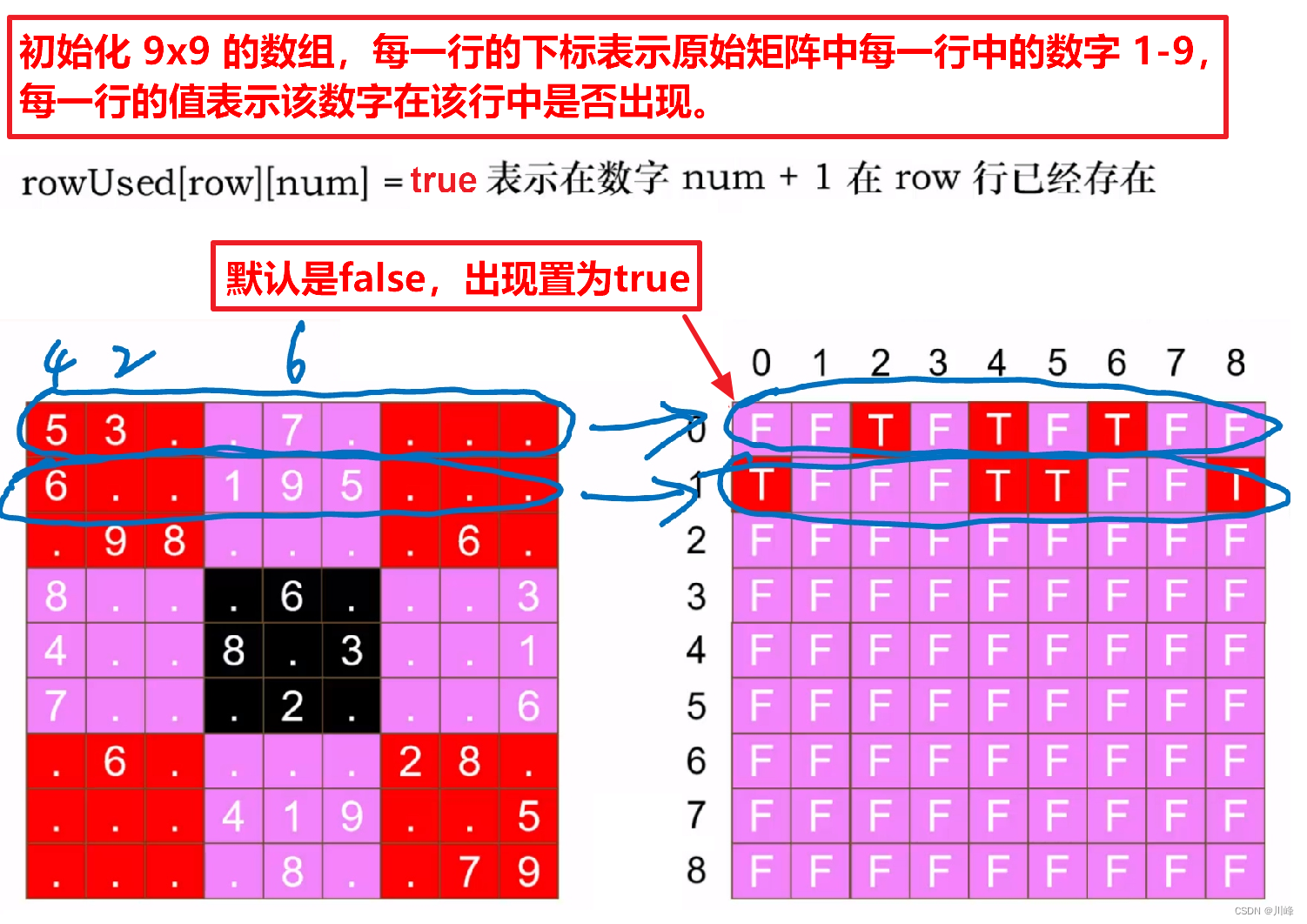
Why is it a 9x9 two-dimensional boolean array here? Because the original matrix has 9 rows, the one-dimensional length is 9, and in each row we need to represent the existence of a total of 9 numbers from 1 to 9, so 9 are needed in each row Array of length.
For columns, the representation is similar:
For a 3x3 small grid, a three-dimensional boolean[3][3][9] array is obviously needed.
251.Expand two-dimensional vectors
-
1) Use list internally to receive, use the corresponding method of list.iterator() , use iterator.next(), iterator.hasNext() , the code is omitted.
-
2) Double pointers use two variables row and col to point to one-dimensional and two-dimensional subscript indexes respectively. When the inner layer reaches the end, row wraps and the next layer col starts from the beginning, skipping empty lines.
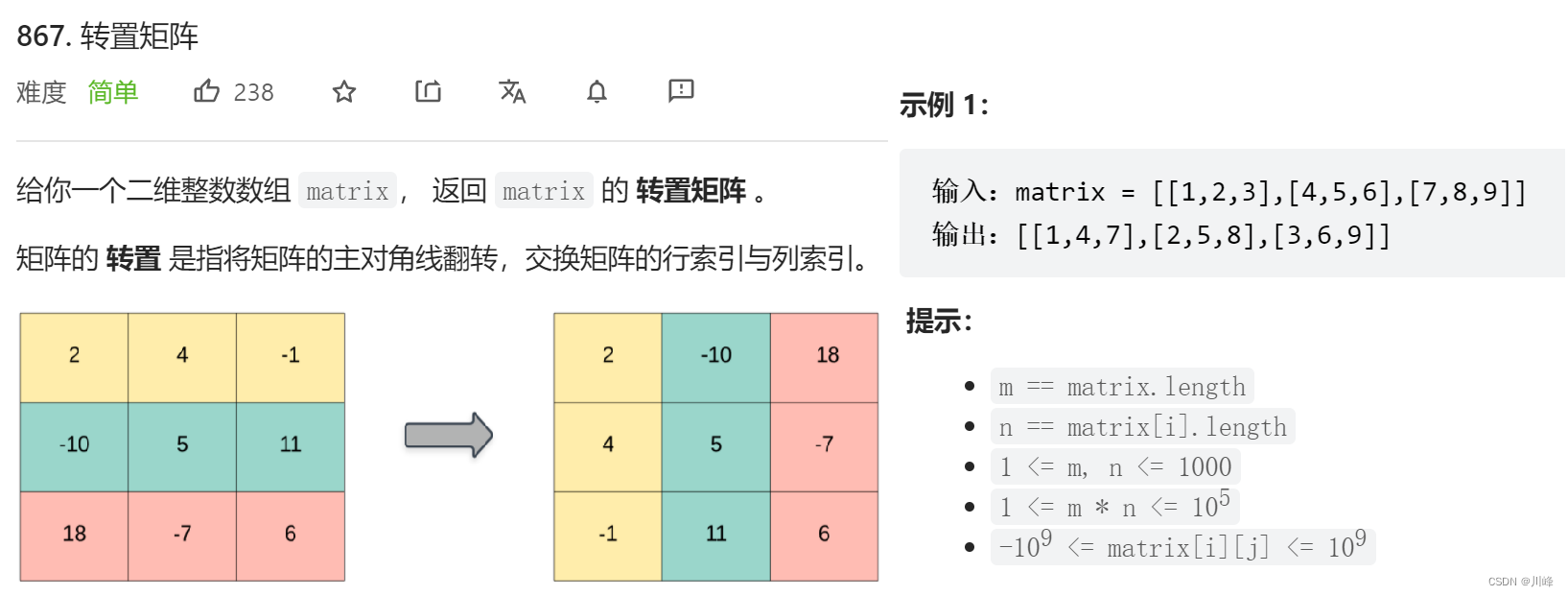
867.Transpose matrix
-
For a matrix with M rows and N columns, create an array res with N rows and M columns ( the rows and columns are swapped ), and then traverse the matrix and save it. res[j][i] = matrix[i][j] swap the row and column coordinates when saving . That’s it
-
Note the difference from [ 48. Rotate image ] . The rotation matrix is a clockwise rotation. This question is just a mirror flip along the upper left-lower right diagonal.
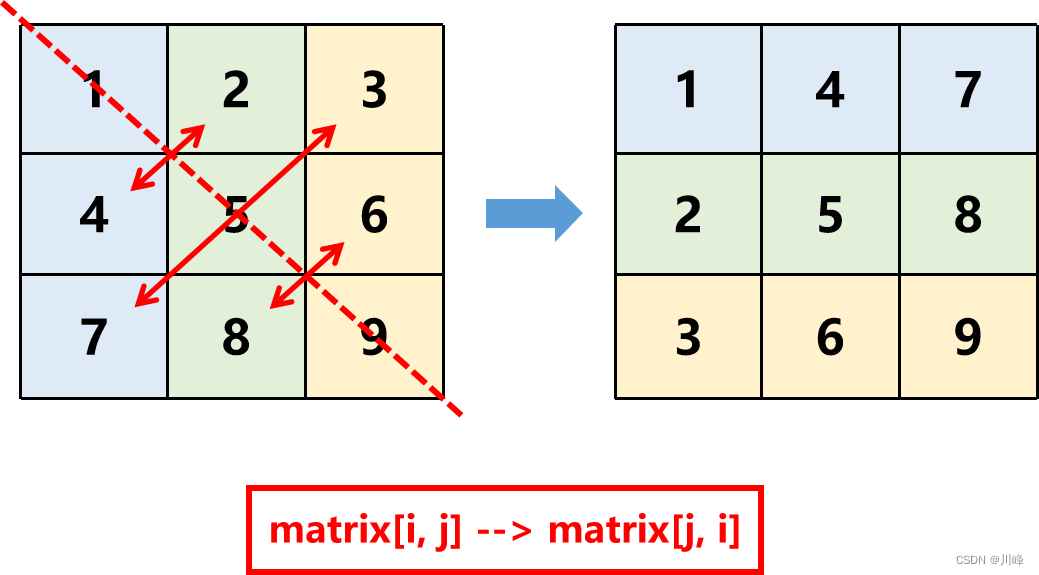
You can imagine pinching the lower left corner of the card with your fingers, and then flipping it toward the upper right corner along the upper left-lower right diagonal line.
Why does the result array here have N rows and M columns? Because the question matrix is not necessarily square. For example, in the 3x2 matrix in the figure below, matrix[2][0] should be stored in matrix[0][2] after flipping. If the result The rows and columns of the array are misaligned and obviously cannot be saved.
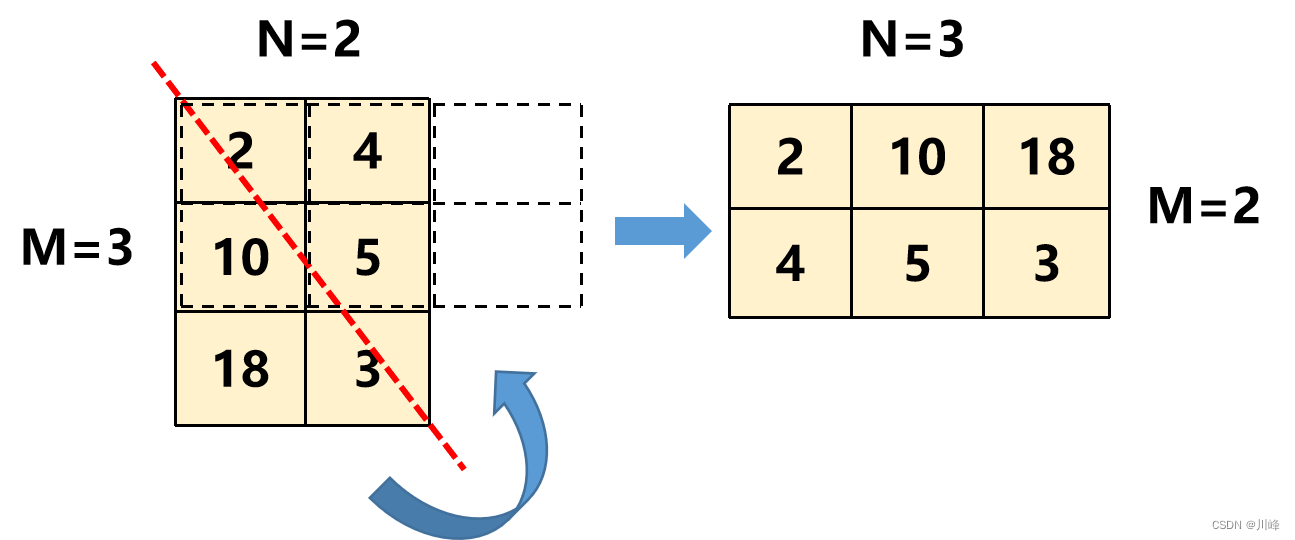
Of course, you can also write it in another way, and swap the subscripts to the values in the original matrix according to the way of traversing the result matrix:
304. Two-dimensional region sum retrieval - matrix immutable
-
1) Two-dimensional prefix sum array , using the idea of finding the area , define S(i, j) to represent the area of the rectangle in the two-dimensional matrix with [0, 0] as the upper left corner and [i, j] as the lower right corner,
-
Then there is S(i, j) = S(i - 1, j) + S(i, j - 1) - S(i - 1, j - 1) + matrix[i][j]
-
Therefore sumRegion(x1, y1, x2, y2) = S(x2, y2) - S(x1-1, y2) - S(x2, y1-1) + S(x1-1, y1-1)
Each grid in the two-dimensional prefix sum array records "the current position is the lower right corner of the area, and the upper left corner of the area is always the area sum of the upper left corner of the original array." If you feel it is not clear, please change S[i] [ j] is understood as the area sum with (i, j) as the lower right corner and (0, 0) as the upper left corner.
The diagram of S[ i, j ] is as follows:
The diagram of S[ i - 1, j ] is as follows:
The diagram of S[ i, j - 1 ] is as follows:
The diagram of S[ i - 1, j - 1 ] is as follows:
So, together we get:
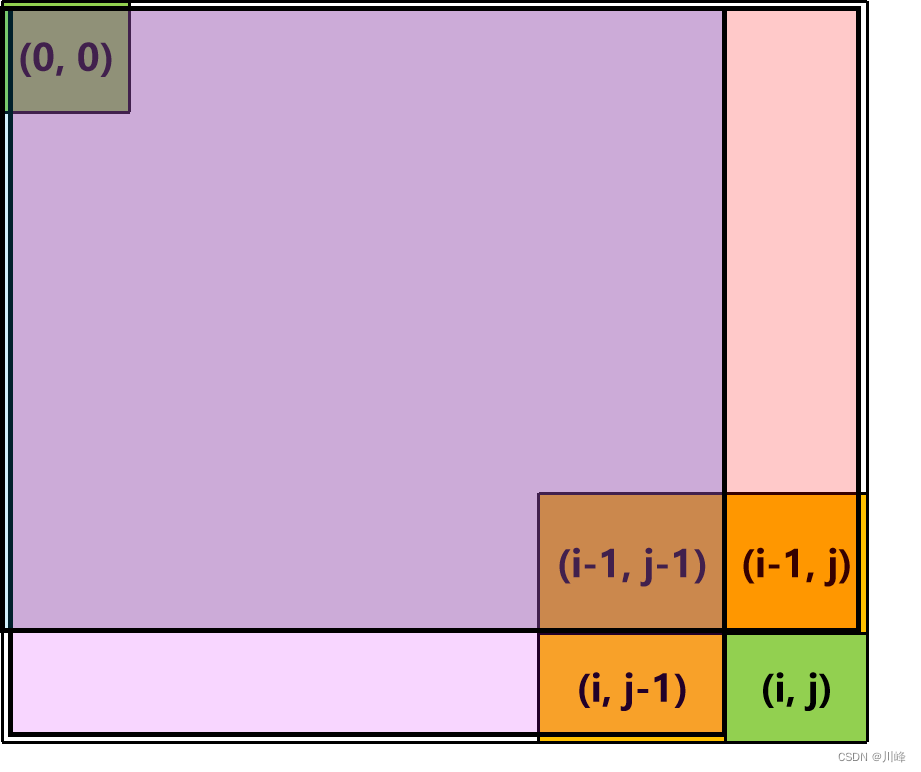
S[ i, j ] is equivalent to S[ i - 1, j ] + S[ i, j - 1 ] + matrix[i, j] but one S[ i - 1, j - 1 ] is added multiple times . Therefore, one needs to be subtracted S[ i - 1, j - 1 ]
With the calculation formula of S[ i, j ] , we scan the original matrix and calculate the value of S[ i, j ] for each grid , thus obtaining a two-dimensional prefix sum array. When we require (x1, y1) as the upper left corner and (x2, y2) as the area sum of the lower right corner, we can directly use the prefix sum array to quickly solve:
The sum of the area from [x1, y1] to [x2, y2] is equivalent to the sum of the area with [x2, y2] as the lower right corner minus the sum of the area lying above with [x1 - 1, y2] as the lower right corner. , and then subtract the sum of the area on the left with [x2, y1 - 1] as the lower right corner, but the sum of the area with [x1 - 1, y1 - 1] as the lower right corner is subtracted multiple times, so it needs to be added The previous area sum with [x1 - 1, y1 - 1] as the lower right corner.
Note that in order to facilitate the calculation and processing of boundary conditions, the prefix and the length of the array are each added by 1 , which is equivalent to adding a blank row with all values 0 to the left and top of the original matrix. This is the idea of defensive programming. At this time, the meaning of prefixSum[i][j] is to represent the cumulative sum of the two-dimensional area composed of the first i rows and the first j columns (counting from 1 ) in the original matrix. That is to say, the subscript in prefixSum means number, so when calculating sumRegion , you can convert the parameter index subscript into a number subscript, so that it matches the calculation formula summarized earlier.
-
2) Find the prefix sum of each row , and find a prefix sum array for each row. There are M prefix sum arrays in M rows. When finding sumRegion , you actually traverse each row of [ row1... row2] and use the row The difference between the prefix and the array is used to find the sum of the [ col1...col2 ] intervals of the row, and then the results of each row are accumulated.
This idea is simpler than method 1. (Although method 1 is more efficient when finding sumRegion)
308. 2D Region and Retrieval - Variable
-
Find the prefix sum of each row , the same as method 2 of Question 304 , use the difference of the prefix sum to find the regional sum, but there is an additional update method. When updating, we only need to add the prefix to the col column of the row in the array The value of each subsequent prefix sum is added to the current updated increment.
363. The maximum value sum of the rectangular area does not exceed K
-
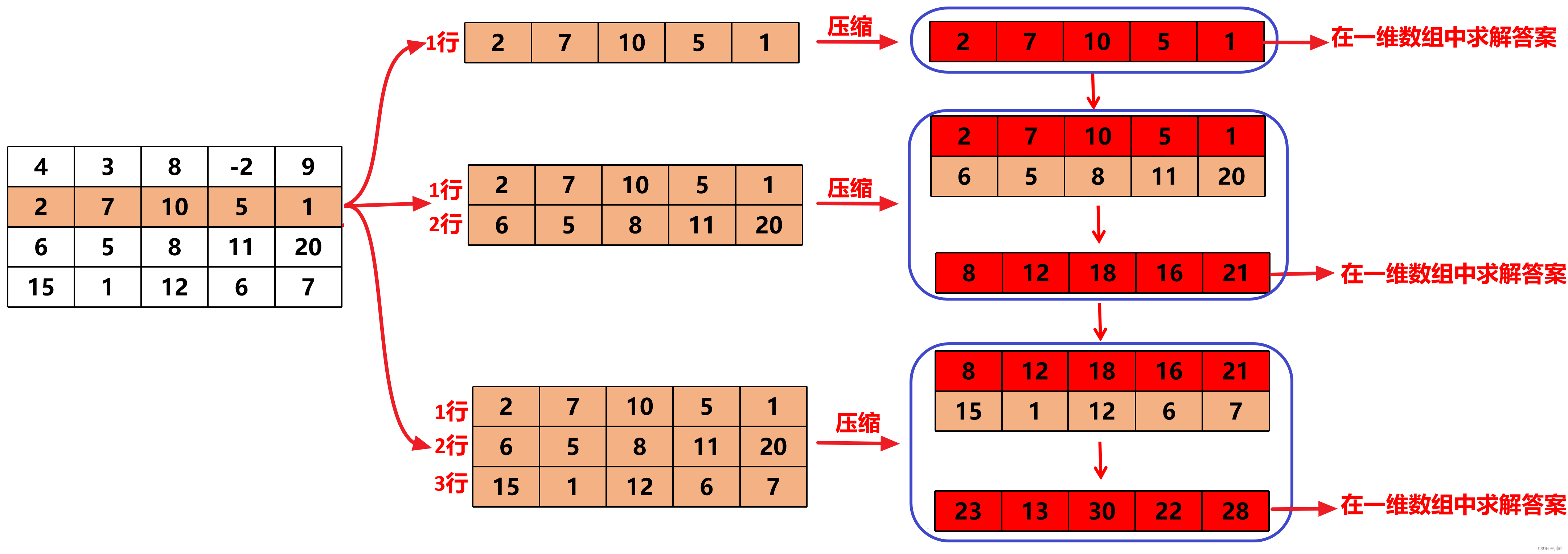
Compress a two-dimensional array into a one-dimensional array (array compression techniques)
-
The outer for loop traverses each row of [0, M - 1] , marked s under the row , and creates a one-dimensional array arr with the same length as the number of columns each time , which is used to save the compression result of the [s..i] row.
-
The inner loop selects the current s row as the starting row each time , traverses [s, M - 1] , and accumulates the current i- th row into arr each time . At this time, arr only contains the elements from row s to row i. and (i.e. lines s..i are now compressed into one line ). Then each time in the one-dimensional array arr compressed by rows s..i , just find the maximum cumulative sum of sub-arrays ≤ k .
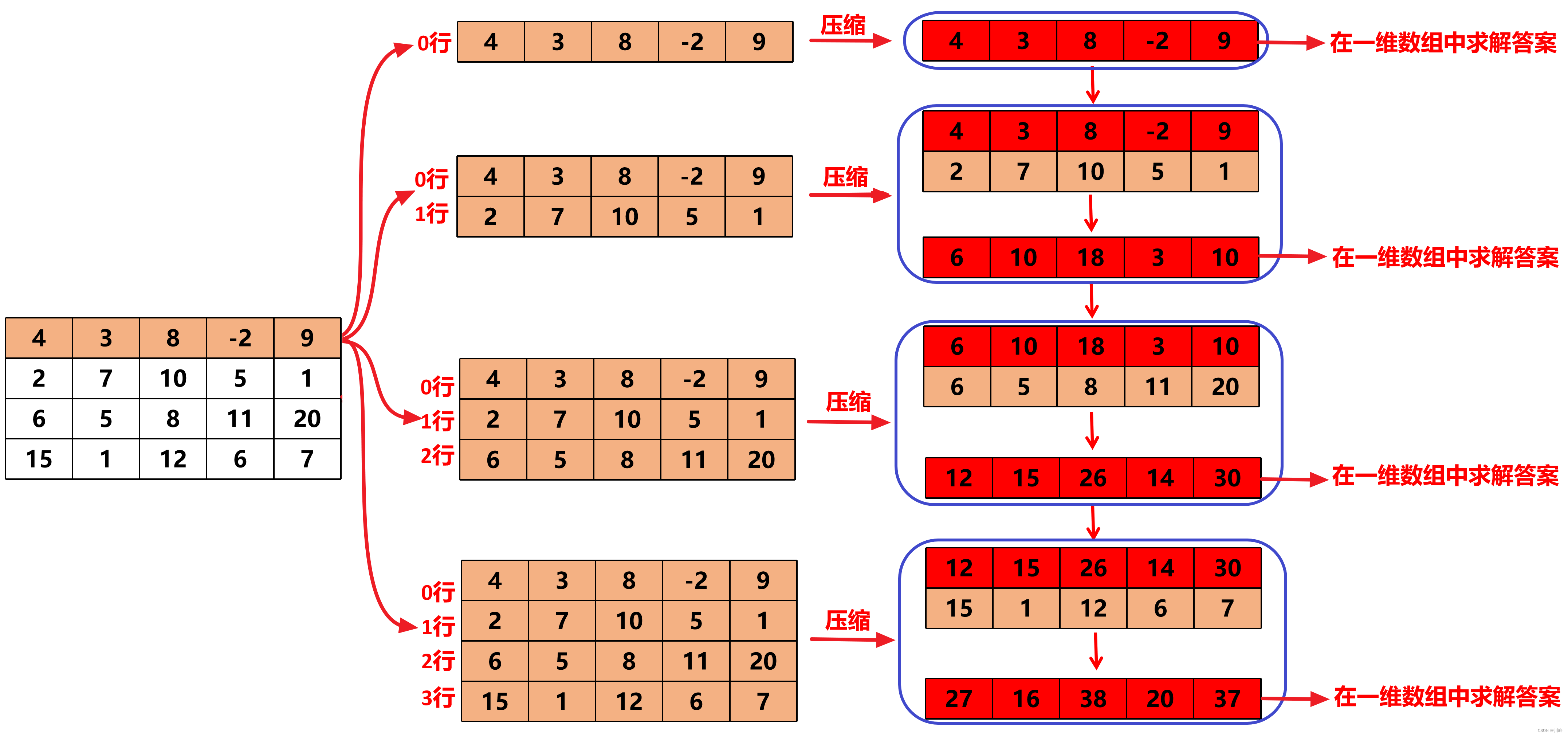
This process actually starts from line 0 and increments by 1 line each time until the lines including all lines are compressed into one line. Solve in the compressed line:
In this way, all rectangular areas starting from row 0 will be scanned, and no one will be missed.
The processing starting from row 1, starting from row 2, and starting from row 3 is similar, and the solution is solved after each compression:
Through the above process, we can first write the main process code:
Now, we only have one last question left, which is how to implement the getMaxNearK() method in the above code
-
① First calculate the maximum value max of the cumulative sum in the one-dimensional array . If max does not exceed k , just return max directly . There is no need to continue searching.
-
② Otherwise, a double-layer for loop is used to violently calculate the cumulative sum of each sub-interval. The outer enumeration i: [0, N - 1] starts with each i , and the inner enumeration j: [i, N - 1] each At the end of j , the inner loop continuously accumulates arr[j] into sum . Because j is enumerated starting from i , so every time sum is updated , we get an accumulation of [i...j] intervals. and, at this time we judge that if sum ≤ k is satisfied , just record the maximum value.
Implementation code:
Let me explain a little more in the first for loop in the above code, when sum <= 0, why should we start accumulating from the current number again: because if sum is a negative number, [continue accumulating the current number] will not be better than [only use the current number] Itself as the cumulative sum] the benefit is greater (there is a bit of greed here). For example, sum = -10, arr[i] = -5. If you continue to accumulate, the income will not increase but decrease. For another example, sum = -10, arr[i] = 12, if accumulated, the result is 2, but if arr[i] is taken directly without accumulation, 12 is obtained.
2) The classic way to solve the cumulative sum of sub-arrays is to use the difference between the prefix and the array . Therefore, we can first calculate the prefix and array for arr , and then double for loops enumerate the sub-ranges of each prefix and array, and the outer enumeration i: [0, N - 1] , inner enumeration j: [0, i] , use prefixSum[i + 1] - prefixSum[j] to get the cumulative sum of the interval [i...j] , judge It is enough whether ≤ k .
Implementation code:
Implementation code:
Note: In the ordered list TreeSet , TreeSet.ceiling(x) returns the minimum value >=x and closest to x ! floor(x) returns the maximum value <=x and closest to x !
Among the three methods for calculating the maximum cumulative sum of subarrays ≤ k in a one-dimensional array, I think method 2) is the best to understand, and method 3) is an improved version of method 2), but due to the amount of data in the question Not much, the brute force method of method 1) is the most efficient (the least time-consuming among the Java versions submitted on LeetCode). When the amount of data is large, method 3) will be more efficient.
The minimum time complexity of this question can reach O(N^3). If brute force is used, it may require O(N＾6). (Because finding the submatrix requires O(N＾4) to find and then traverse the summation is O(N＾2))
An interview question similar to this question:
Given a two-dimensional matrix of integers, return the maximum cumulative sum of the submatrices.
Problem-solving idea: This question is simpler than the original question. There is no limit of ≤ k. The main idea is the same as above. We can directly calculate the maximum value of the cumulative sum while compressing. There is no need to separately calculate the maximum cumulative value of ≤ k. And.
The implementation code is as follows:
Here, when sum < 0 , the sum is cleared to 0 to maintain the maximum benefit of the cumulative sum, because the cumulative sum benefit obtained by continuing to accumulate a negative number with a certain number will not be greater than the benefit of just taking the number itself as the cumulative sum (greedy ). Specific examples are listed in method 1) among the three methods for calculating the maximum cumulative sum of subarrays ≤ k in a one-dimensional array. You can read it.
348. Design Tic Tac Toe
-
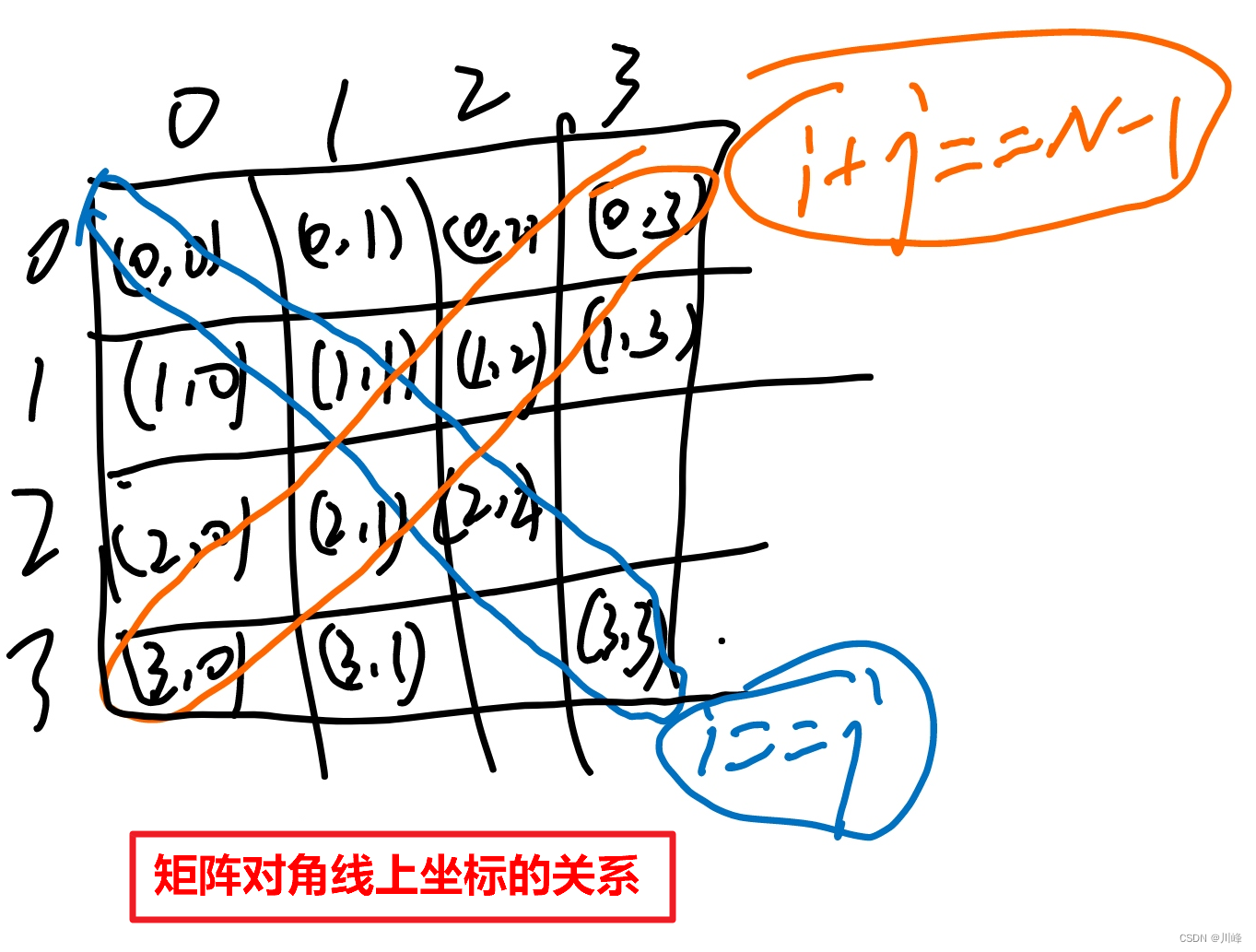
Use three two-dimensional arrays to record the number of chess pieces placed by player X on each row, each column, and each diagonal. In each move method, add the count in the three arrays corresponding to the current player + 1 , if the count in an array reaches N , then the player wins and the player's serial number is returned.
-
Tip: In the matrix of NXN , the point whose coordinate point satisfies i == j is located on the main diagonal (upper left-lower right), and the point whose coordinate point satisfies i + j == N - 1 is located on the sub -diagonal (upper right-lower left) . )
296. Best meeting place
-
1. Sorting + median , Manhattan distance is actually the sum of sub-problems of two independent variables . Therefore, as long as we solve the one-dimensional case, we can treat the two- dimensional case as the sum of two one-dimensional independent sub-problems .
-
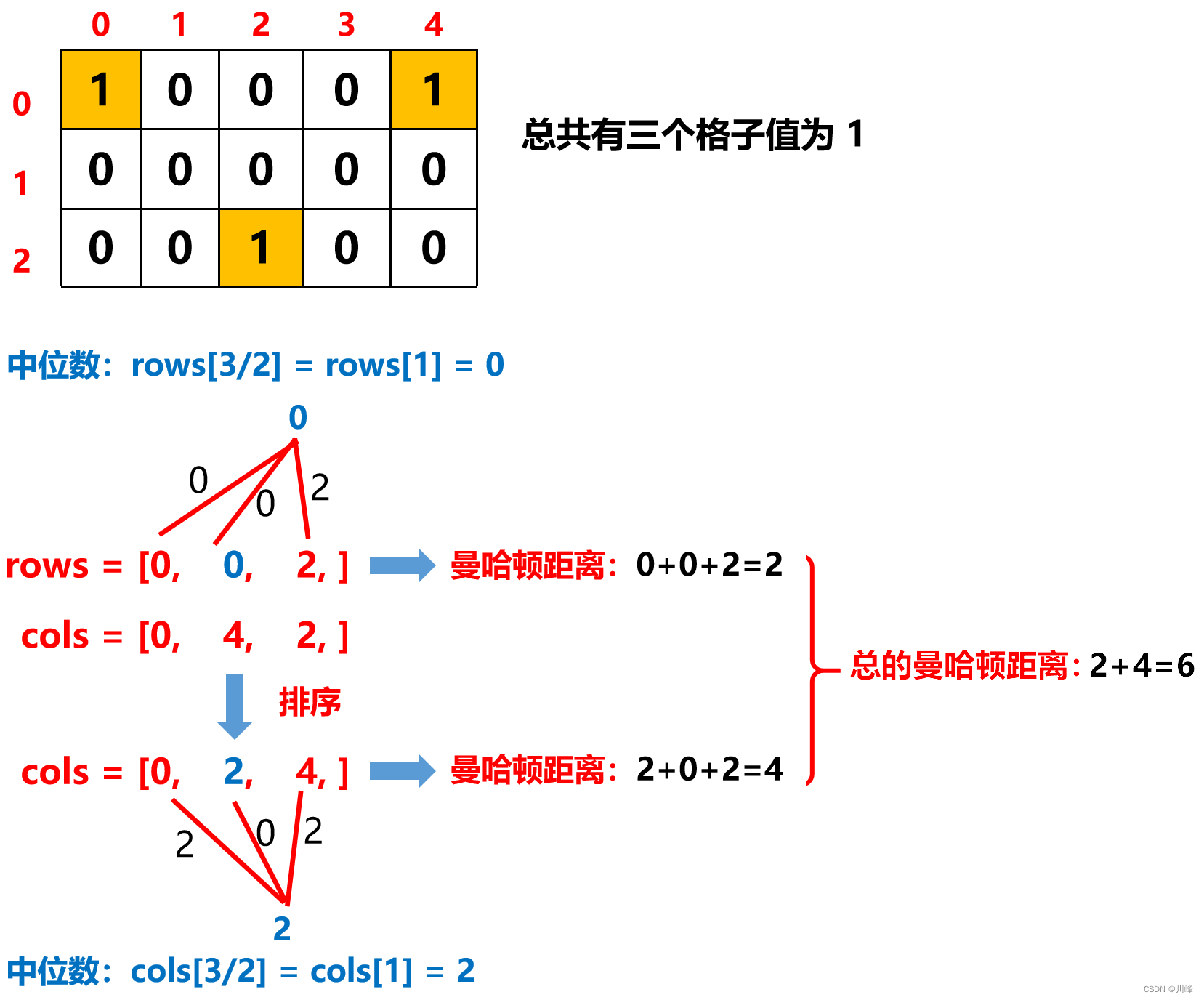
The median is the optimal meeting point . As long as there are the same number of points to the left and right of the meeting point, the total distance is minimal .
-
First, we traverse the original matrix and only process the grid with a value of 1. We collect the row coordinates and column coordinates of each grid into a one-dimensional array and sort them . Then we select the elements in the middle of them and calculate two independent ones. The Manhattan distance of the dimensional array, the sum of the two is the answer.
Time complexity O( mnlogmn )
-
2. Collect coordinates + median in order , the same as method 1, except that when collecting the column subscripts of each grid with a value of 1 , we can collect by first traversing the columns and then traversing the rows , so that we collect The column subscripts are already sorted in order , thus eliminating the time complexity of the sorting operation. The time complexity is O(mn).
-
3. Collect coordinates + collision pointers in order , the same as method 2, except that when calculating the Manhattan distance of a one-dimensional array, you no longer need to know the median, you only need to set a pair of collision pointers L and R , let L and R approaches from both ends of the array to the middle, and continuously accumulates the numerical difference points[R] - points[L] at both ends .
