1. Generation of common distributed random numbers
1.1 Binomial distribution
In the Benoit experiment, the probability of an event A occurring is p, and the experiment is repeated n times. X represents the number of times A occurs in these n experiments. Then the probability distribution law (probability density) of the random variable
recorded as ![]()
thispdf(x,n,p) pdf('this',x,n,p)
Returns the density function value (probability distribution law value) of the binomial distribution at x with parameters n and p.
>> clear
>> x=1:30;y=binopdf(x,300,0.05);
plot(x,y,'b*')

binocdf(x,n,p) cdf('bino',x,n,p)
Returns the distribution function value of the binomial distribution at x with parameters n and p
>> clear
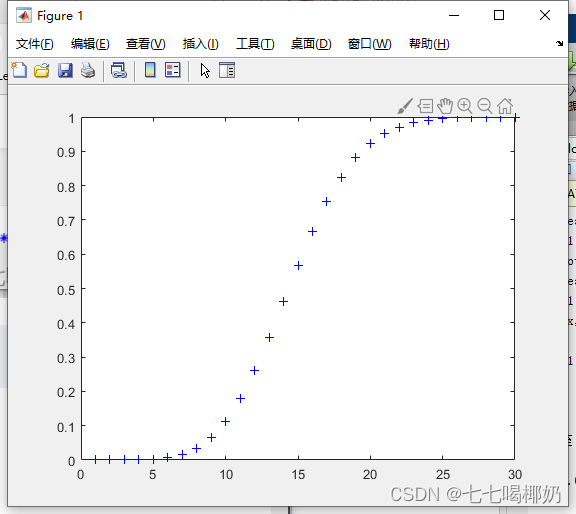
>> x=1:30;y=binocdf(x,300,0.05);
>> plot(x,y,'b+')
icdf('bino',q,n,p)
Inverse distribution calculation, returns the x value of the distribution function of the binomial distribution with parameters n and p when the probability is q.
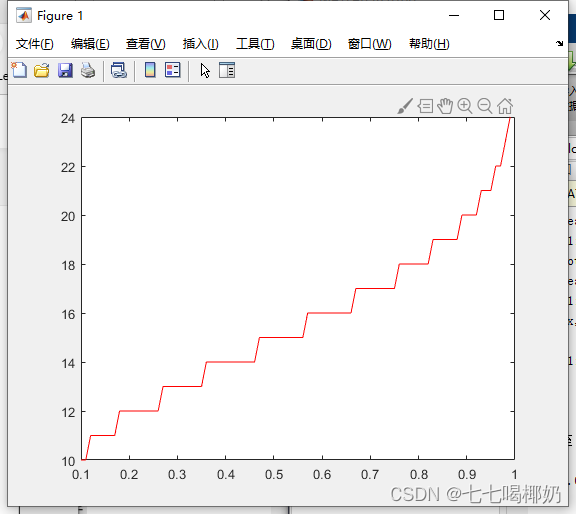
>> p=0.1:0.01:0.99;
>> x=icdf('bino',p,300,0.05);
>> plot(p,x,'r-')
R=binornd(n,p,m1,m2)
Generate random data in m1 rows and m2 columns obeying the binomial distribution with parameters n and p.
>> R=binornd(10,0.5,3,4)
R =
0 6 5 5
6 6 5 5
4 5 5 4
>> A=binornd(10,0.2,3)
A =
1 2 2
1 3 1
2 2 2
1.2 Poisson distribution
The Poisson distribution describes density problems: for example, the number of bacteria under the microscope X, the number of people infected with a certain disease in the unit population The number of pieces of information is X, etc.
The distribution law of X is (density function)
Denoted as ![]() where parameter λ represents the average value.
where parameter λ represents the average value.
boypdf(x,lambda) pdf('boy',x,lambda)
Returns the probability value of the Poisson distribution at x with parameter lambda.
>> clear
>> x=0:30;p=pdf('poiss',x,4);
>> plot(x,p,'b+')

boyscdf(x,lambda) cdf('boy',x,lambda)
Returns the distribution function value of the Poisson distribution at x with parameter lambda: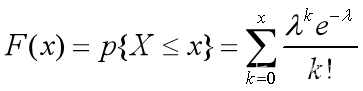
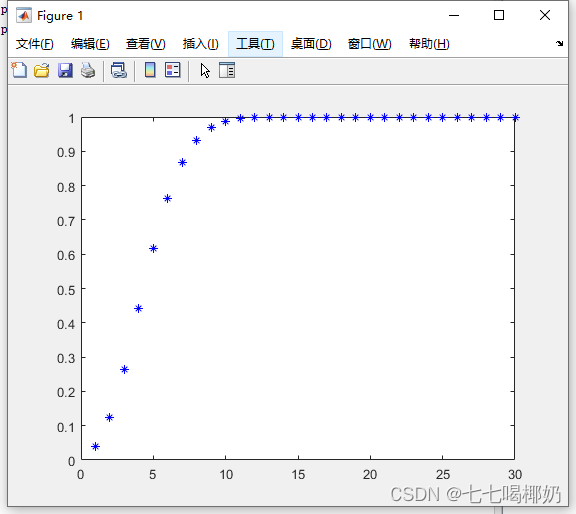
>> x=1:30;
>> p=cdf('poiss',x,5);
>> plot(x,p,'b*')
poissrnd(lambda,m1,m2)
Returns a random number in row m1 and column m2 that obeys the Poisson distribution with parameter lambda.
>> poissrnd(10,3,4)
ans =
15 10 9 7
14 10 7 9
10 9 14 10
>> poissrnd(10,3)
ans =
14 11 8
8 11 13
5 10 11
1.3 Geometric distribution
In a Bernoulli trial, the probability of success in each trial is p, and the probability of failure is q=1-p,0<p<1. The first successful trial occurs at the Xth time, then the distribution law of X is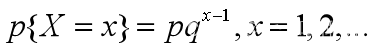
geopdf(x,p)
Returns the probability value at x that obeys the geometric distribution with parameter p.
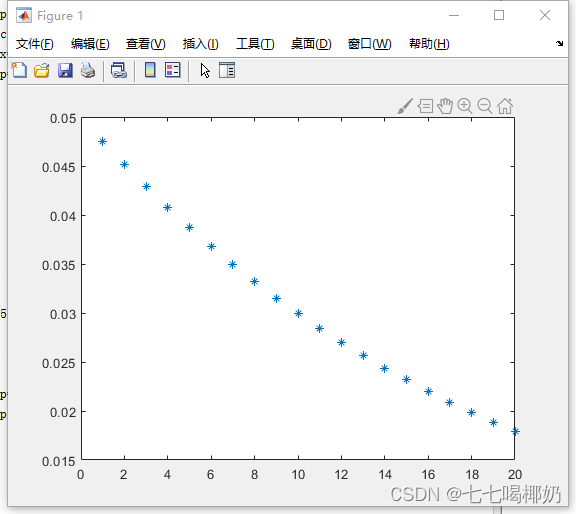
>> x=1:20;
>> p=geopdf(x,0.05);
>> plot(x,p,'*')
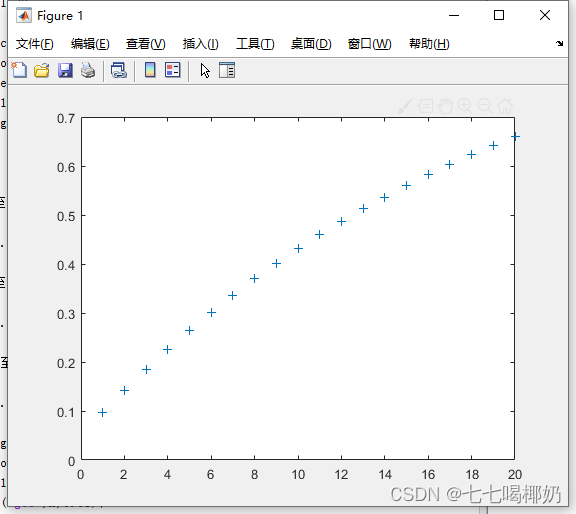
>> x=1:20;
>> p=cdf('geo',x,0.05);
>> plot(x,p,'+')
Returns the distribution function value
>> R=geornd(0.2,3,4)
R =
0 0 5 0
0 2 2 8
9 10 0 0
>> R1=geornd(0.2,3)
R1 =
0 8 1
3 3 0
0 0 1
1.4 Uniform distribution (discrete, equally likely distribution)

>> x=1:20;
>> p=unidpdf(x,20);f=unidcdf(x,20);
>> plot(x,p,'*',x,f,'+')

>> R=unidrnd(20,3,4)
R =
1 14 8 15
17 16 14 1
19 15 4 6
>> R=unidrnd(20,3)
R =
1 14 1
2 7 9
17 20 8
1.5 Uniform distribution (continuous type, etc. possible)

>> clear
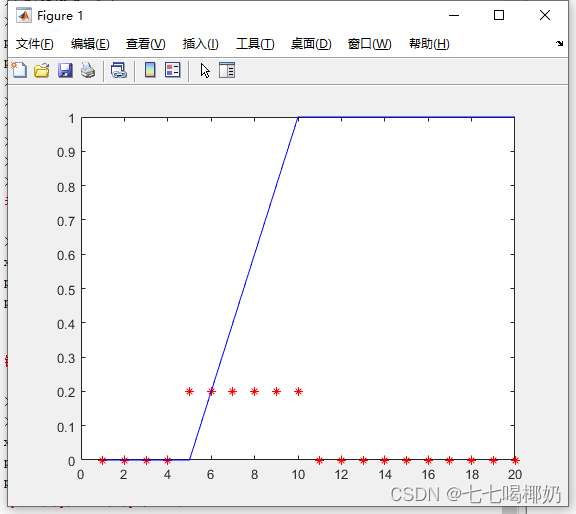
>> x=1:20;p=unifpdf(x,5,10);
>> p1=unifcdf(x,5,10);
>> plot(x,p,'r*',x,p1,'b-')
>> R=unifrnd(5,10,3,4)
R =
8.8276 7.4488 8.5468 8.3985
8.9760 7.2279 8.7734 8.2755
5.9344 8.2316 6.3801 5.8131
>> R1=unifrnd(5,10,3)
R1 =
5.5950 6.7019 8.7563
7.4918 7.9263 6.2755
9.7987 6.1191 7.5298
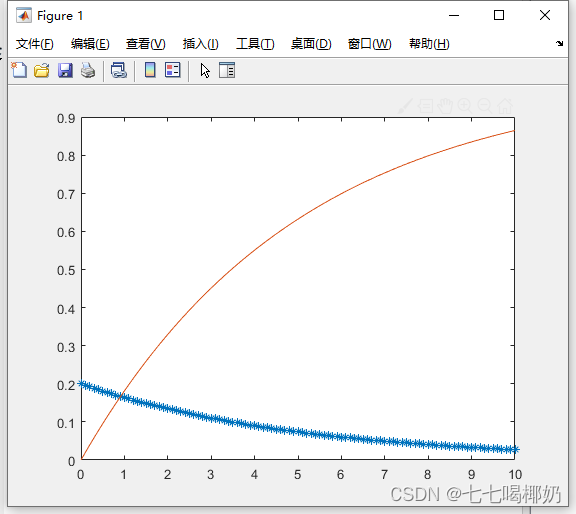
1.6 Exponential distribution (describing the "lifetime" problem)
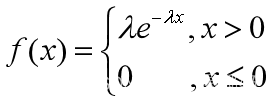
>> x=0:0.1:10;
p=exppdf(x,5);
p1=expcdf(x,5);
plot(x,p,'*',x,p1,'-')
>> R=exprnd(5,3,4)
R =
1.7900 3.0146 6.7835 1.0272
0.5776 9.8799 0.8675 7.0627
0.2078 9.5092 6.8466 0.3668
>> R1=exprnd(5,3)
R1 =
5.2493 2.4222 0.9267
8.1330 3.7402 2.6785
6.9098 5.2255 2.9917
1.7 Normal distribution
![]()
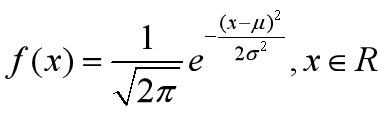
clear
x=-10:0.1:15;
p1=normpdf(x,2,4);p2=normpdf(x,4,4);p3=normpdf(x,6,4);
plot(x,p1,'r-',x,p2,'b-',x,p3,'g-'),
gtext('mu=2'),gtext('mu=4'),gtext('mu=6')

clear
x=-10:0.1:15;
p1=normpdf(x,4,4);p2=normpdf(x,4,9);p3=normpdf(x,4,16);
plot(x,p1,'r-',x,p2,'b-',x,p3,'g-'),
gtext('sig=2'),gtext('sig=3'),gtext('sig=4')

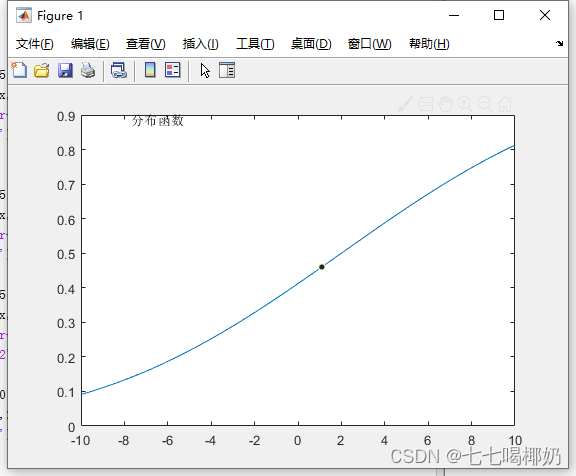
>> clear
>> x=-10:0.1:10;
>> p=normcdf(x,2,9);
>> plot(x,p,'-'),gtext('分布函数')
>> p=[0.01,0.05,0.1,0.9,0.05,0.975,0.9972];
>> x=icdf('norm',p,0,1)
x =
-2.3263 -1.6449 -1.2816
1.2816 -1.6449 1.96 2.7703
x=icdf('norm',p,0,1)
Calculate the inverse function value of the distribution function of the standard normal distribution, that is, return the corresponding quantile if the probability is known.
Generate normally distributed random numbers
>> R=normrnd(0,1,3,4)
R =
1.5877 0.8351 -1.1658 0.7223
-0.8045 -0.2437 -1.1480 2.5855
0.6966 0.2157 0.1049 -0.6669
>> R1=normrnd(0,1,3)
R1 =
0.1873 -0.4390 -0.8880
-0.0825 -1.7947 0.1001
-1.9330 0.8404 -0.5445