The full name is Zero-Knowledge Succinct Non-Interactive Argument of Knowledge, a concise non-interactive zero-knowledge proof. The simplicity makes the protocol run, even if the statement is very large, its proof size is only a few hundred bytes, and a proof is verified The time can reach millisecond level.
The main scenario to be solved is that Prover proves to Verifier that the calculation result of a commonly recognized computational problem is correct, requires zero knowledge, and cannot disclose any information.
The core method is to use R1CS, QAP and other methods to turn computational problems into polynomials, cleverly transform the correctness of calculation results into polynomial problems with special solutions, generate corresponding proofs, and then use polynomial proof methods to complete the proof and verification.
Non-Interactive Argument of Knowledge of a Polynomial
(Note that the calculation and parameter selection are in the domain, that is, modulo operation)
Proof of General Polynomials
The scenario is as follows: Verifier has a polynomial f ( x ) f(x)f ( x ) , Prover proves to Verifer that he knows this polynomial.
Suppose the polynomial known by the Prover isp ( x ) p(x)p ( x ) , then what we need to prove now isf ( x ) = p ( x ) f(x)=p(x)f(x)=p ( x ) , if the two polynomials are of order up toddd , then the curve represented by the two polynomials will have at mostddd intersection points, when the Verifier randomly takes a value ssin a large ranges , thensss andddThe probability of d being the same will be very low, so there is the following agreement
- Verifier randomly selects a value ss in a large ranges , and locally computef ( s ) f(s)f ( s ) , then putsss to Prover
- Prover calculates p ( s ) p(s)p ( s ) , then sent to Verifier
- Verifier verifies f ( s ) = ? p ( s ) f(s)\overset{?}=p(s)f(s)=?p(s)
Proving the roots of a polynomial
Some polynomials can decompose the product of multiple polynomials, such as assuming p ( x ) = ( x − a ) ( x − b ) ( x − c ) p(x)=(xa)(xb)(xc)p(x)=(x−a)(x−b)(x−c ) Then
suppose Prover has a polynomialp ( x ) p(x)p ( x ) , now he wants to prove that his polynomial holds some roots (partial polynomial), that is, prove that his polynomialp ( x ) = t ( x ) h ( x ) p(x)=t(x)h (x)p(x)=t ( x ) h ( x ) containst ( x ) t(x)t ( x ) is assumed to be( x − a ) ( x − b ) (xa)(xb)(x−a)(x−b ) , and at this timet ( x ) t(x)t ( x ) is called the target polynomial, which is public. It should be noted that the Prover cannot reveal the original polynomial. Then there is the following protocol
- Verifier randomly selects the value ss in a large ranges , calculatet = t ( s ) t = t(s)t=t ( s ) , thensss to Prover
- Proer calculates h ( x ) = p ( x ) t ( x ) h( x ) = \frac {p(x)}{t(x)}h(x)=t(x)p(x), h ( s ) h(s) h(s), p ( s ) p(s) p ( s ) , then send the last two to Verifier
- Verfier verify p ( s ) = ? t ( s ) h ( s ) p(s)\overset{?}=t(s)h(s)p(s)=?t(s)h(s)
It is obvious that the above variables are all limited to integers, if ppp does dividettt , then the equation must be established, if not, then there will be a remainder in the formula, and there is a great probability that it is not an integer.
Of course, this protocol still has a lot of loopholes, for example, Prover may not knowp ( x ) p(x)p ( x ) , but knowing the publict ( x ) t(x)t ( x ) , so h ( x ) can be completely fabricatedh(x)h ( x ) satisfies the condition.
homomorphic encryption
Obviously, we cannot transmit plaintext in the protocol, but we need to calculate ciphertext, so we need an algorithm that satisfies both encryption and calculation characteristics.
Homomorphic encryption algorithm E ( x ) E(x)E(x),如 E ( a x + b y ) = g a x + b y = g a x ⋅ g b y = ( g x ) a ⋅ ( g y ) b = E ( x ) a ⋅ E ( y ) b . E(a x+b y)=g^{a x+b y}=g^{a x} \cdot g^{b y}=\left(g^{x}\right)^{a} \cdot\left(g^{y}\right)^{b}=E(x)^{a} \cdot E(y)^{b} . E ( at x+by)=gax+by=gax⋅gby=(gx)a⋅(gy)b=E ( x )a⋅E ( and )b.( g g g is the generator), based on the discrete logarithm problem and the CDH assumption (that is, givenga , gbg^a,g^bga,gb , getgabg^{ab}gab is difficult). Obviously, this is homomorphic encryption that only satisfies homomorphic addition, and does not support ciphertext multiplication.
Then the algorithm does not support multiplication, only onessIn the case of s , how to calculate the polynomial homomorphically? Obviously not, so I tried to convert homomorphic multiplication into homomorphic addition, and noticed that the polynomialP ( x ) P(x)P ( x ) can be regarded as a linear combination of a set of coefficients and unknowns, that is, to calculatessEach power of s , which needs to fix the order ddd , which is equivalent to limiting the order of the polynomial, so thats 1 , … , sds^1,\dots,s^ds1,…,sd , and then calculate the addition of each part of the polynomial.
The specific use is as follows,
- Verifier randomly selects an ss in a large ranges , calculate ssfirstPower of s 1 , … , sds^1,\dots,s^ds1,…,sd , then calculatet ( s ) t(s)t(s),最后 E ( 1 ) , E ( s ) , … , E ( s d ) E(1),E(s),\dots,E(s^d) E(1),E(s),…,E(sd )and sent to Prover
- Prover calculates after receiving the data, h ( x ) = p ( x ) t ( x ) h( x ) = \frac {p(x)}{t(x)}h(x)=t(x)p(x), and then calculate E ( p ( s ) ) E(p(s)) with the coefficients of the polynomialE(p(s)), E ( h ( s ) ) E(h(s)) E ( h ( s )) and send to Verifier
- Verifier for verification E ( p ( s ) ) = ? E ( t ( s ) ) E ( h ( s ) ) E(p(s))\overset{?}=E(t(s))E(h( s))E(p(s))=?E(t(s))E(h(s)),即 g p ( s ) = ( g h ( s ) ) t ( s ) g^{p(s)} = (g^{h(s)})^{t(s)} gp(s)=(gh(s))t(s)
** KCA(The Knowledge of Coefficient Test and Assumption)**
The above protocol still has a lot of loopholes. For example, when Prover calculates polynomials, he does not use the format of polynomials (linear combination of constant coefficients and unknowns), but uses another method. The algorithm finds an algorithm that satisfies zp = ( zh ) t ( s ) z_p = (z_h)^{t(s)}zp=(zh)Two values of t ( s ) zp , zh z_p, z_hzp,zhTo replace gp ( s ) , gh ( s ) g^{p(s)},g^{h(s)}gp(s),gh ( s ) , that is, no polynomial is used at all, and the result that satisfies the condition is directly imitated.
Here it is necessary to restrict Prover, so that he must use a polynomial that satisfies the conditions, which is limited to a constant, and the exponent is also limited, and the exponent cannot be changed arbitrarily. SoKCAcan also be calledKEA(Knowledge of exponent)
as follows,
define a pair of elements( a , b = α ⋅ a ) (a,b = \alpha \cdot a)(a,b=a⋅a ) (called anα \alphaα - 对),α ⋅ a \alpha \cdot aa⋅a meansα \alphaaaaaa __a addition, that is,a α a^\alphaaα , then a KC process is as follows:
- First Verifier will randomly select a non-zero α \alphaα,calculationb= α ⋅ ab = \alpha \cdot ab=a⋅a , obviously this is anα − shift \alpha -shifta−shift。
- Verifier sends this challenge pair ( a , b ) (a,b)(a,b ) To Prover.
- At this time, Prover will respond a pair of different, but with the same nature pair ( a ′ , b ′ ) (a',b')(a′,b′ ), it should beα − shift \alpha -shifta−shift
- If received is an α − shift \alpha -shifta−s hi f t , then Verifier accepts this response
Note that this satisfies the DL problem, and it is difficult for Prover to find an α \alphaα , then how should she construct a newα − shift \alpha -shifta−What about shift ? _ In an obvious way, Prover chooses a constant coefficientγ \gammaγ , direct construction( a ′ , b ′ ) = γ ( a , b ) (a',b') = \gamma(a,b)(a′,b′)=c ( a ,b ) .
Suppose Verifier sends not one, butddd组 α − s h i f t \alpha -shift a−s hi f t , then Prover will also choose a set of coefficientsc 1 , … , cd c_1,\dots,c_dc1,…,cd,respond 一个
( a ′ , b ′ ) = ( ∑ i = 1 d c i a i , ∑ i = 1 d c i b i ) (a',b') = (\sum_{i=1}^d c_ia_i,\sum_{i=1}^d c_ib_i) (a′,b′)=(∑i=1dciai,∑i=1dcibi) , obviously this pair also satisfiesα − shift \alpha -shifta−s hi ft . _ If the content sent by Verifier is optimized, it constitutesKCA.
Blind Evaluation of Polynomials Verifiable Protocol
A complete polynomial blind verification protocol.
Two properties need to be satisfied to solve the whole problem:
- **Blindness: **That is, Prover cannot obtain sss , the same Verifier can not getp ( x ) p(x)p ( x ) (homomorphism).
- **Verifiability:** is to ensure that the Prover sends E ( p ( x ) ) E(p(x))E ( p ( x )) is indeed a polynomialp ( x ) p(x)p ( x ) is calculated instead of completely uncorrelated data (KCA)
Then use KCA to optimize the previous protocol as follows,
- Verifier randomly chooses α \alphaα (non-zero) andsss , then calculatet ( s ) t(s)t ( s ) , then constructα − shift \alpha -shifta−shift ( g , g α ) , ( g s , g α ⋅ s ) , … , ( g s d , g α ⋅ s d ) (g,g^{\alpha}),(g^s,g^{\alpha \cdot s} ),\dots,(g^{s^d},g^{\alpha \cdot s^d}) (g,ga ),(gs,gα⋅s),…,(gsd,gα⋅sd)
- Prover uses the polynomial p ( x ) p(x)The coefficient c 1 of p ( x ) , … , cd c_1,\dots,c_dc1,…,cd, and then calculate E ( h ( s ) ) E(h(s))E(h(s))以及 ( E ( p ( s ) ) , E ( α p ( s ) ) ) = ( g ∑ i = 1 d c i s i , g ∑ i = 1 d c i α ⋅ s d ) (E(p(s)),E(\alpha p(s))) = (g^{\sum_{i=1}^d c_is^i},g^{\sum_{i=1}^d c_i\alpha \cdot s^d}) (E(p(s)),E(αp(s)))=(g∑i=1dcisi,g∑i=1dciα⋅sd ), sent to Verifier
- Verifier for verification E ( p ( s ) ) = ? E ( α p ( s ) ) E(p(s))\overset ?=E(\alpha p(s))E(p(s))=?E(αp(s))和 E ( p ( s ) ) = ? E ( t ( s ) ) E ( h ( s ) ) E(p(s))\overset{?}=E(t(s))E(h(s)) E(p(s))=?E ( t ( s ) ) E ( h ( s ))
This scheme can also solve the previous problem, that is, the Prover cannot be constructed arbitrarily to satisfy the similar zp = ( zh ) t ( s ) z_p = (z_h)^{t(s)}zp=(zh)h(s) h(s)of t ( s )h ( s ) , so it is easy not to satisfyα − shift \alpha -shifta−Shift constraints . _ _
Parings and bilinear map
The previous protocol basically realizes the interaction scheme between two honest parties. The relevant proof is only valid between the two parties and cannot be reused. However, in practice, there are many malicious parties, which is obviously not realistic. Therefore, some secret parameters need to be reusable or even public, and trusted enough to prevent abuse. First consider the ( t ( s ) , α ) (t(s),\alpha)
generated by Verifier(t(s),α ) for encryption protection to prevent leakage. If the previous homomorphic encryption is used, the subsequent multiplication calculation will involve homomorphic multiplication, but the homomorphic algorithm used earlier does not support homomorphic multiplication. So what should we do when we must use something like multiplication? At this time, the elliptic hyperbolic mapping is introduced.
Parings are multiplicative representation functions that deterministically map two encrypted inputs in one set to an output in another set.
That is:e : G × G → GT e: \mathbb{G} \times \mathbb{G} \rightarrow \mathbb{G}_Te:G×G→GTSatisfy the following properties
e ( g 1 a , g 2 b ) = e ( g 1 , g 2 ) ab = e ( g 1 ab , g 2 ) = e ( g 1 , g 2 ab ) \begin{aligned}e( \mathrm{g_1^a,g_2^b})&=\mathrm{e(g_1,g_2)^{ab}=e(g_1^{ab},g_2)=e(g_1,g_2^{ab})} \end{aligned}e ( g1a,g2b)=e ( g1,g2)ab=e ( g1ab,g2)=e ( g1,g2ab)
e ( g 1 a , g 2 b ) e ( g 1 c , g 2 d ) = e ( g 1 , g 2 ) a b + c d \begin{aligned} e(\mathrm{g_1^a,g_2^b})e(\mathrm{g_1^c,g_2^d})&=\mathrm{e(g_1,g_2)^{ab+cd}}\end{aligned} e ( g1a,g2b) e ( g1c,g2d)=e ( g1,g2)ab+cd
Its significance is that to map a pair of elements in a certain group to a new group, if and only if the products of the corresponding exponents of the two preimages are the same, the images are also the same. Moreover, the function is required to be computable (that is, without brute force search, etc.), and it can verify whether the product of a pair of (encrypted) data is the same as another pair (although the product cannot be calculated) Next
, The calculation of the agreement is placed on the elliptic curve group satisfying Parings.
Multiple Parties Composite Common Reference String
First introduce a trusted third party to randomly generate sss andα \alphaα , and calculatethe CRS(Common Reference String), a total of two parts of proof and verification, both of which are public (i ∈ { 0 , … , d } i \in \{0,\dots,d\}i∈{ 0,…,d } ), then you need to deletesss andα \alphaa .
- Proving Key: E ( s i ) , E ( α s i ) = g s i , g α s i E(s^i),E(\alpha s^i) = g^{s^i},g^{\alpha s^i} E(si),E ( a si)=gsi,gαsi
- Verification Key: E ( t ( s ) ) , E ( α ) = g t ( s ) , g α E(t(s)),E(\alpha) = g^{t(s)},g^{\alpha} E(t(s)),E ( a )=gt(s),ga
Then, based on CRS, Prover and Verifier can complete the agreement only through CRS. Continue to optimize the protocol as follows, (the following simplifies p = p ( s ), t , hp=p(s),t,hp=p(s),t,h is also similar)
- For Prover, the public CRS already contains the content of the first step, and the next step is to use the Proving Key to calculate E ( h ( s ) ) E(h(s))E ( h ( s ))和( E ( p ( s ) ) , E ( α p ( s ) ) ) (E(p(s)),E(\alpha p(s)))(E(p(s)),E(αp(s)))
- For Verifier, Verfication in CRS is used for verification ( p ′ = α p p' = \alpha pp′=α p )
- First verify that p = t ⋅ hp=t \cdot hp=t⋅h,即 e ( g p , g 1 ) = e ( g t , g h ) = e ( g , g ) p = e ( g , g ) t ⋅ h e(g^p,g^1) = e(g^t,g^h) = e(g,g)^p = e(g,g)^{t \cdot h} e ( gp,g1)=e ( gt,gh)=e ( g ,g)p=e ( g ,g)t⋅h
- Then verify α − shift \alpha -shifta−shift,即 e ( g p , g α ) = e ( g p ′ , g ) e(g^p,g^\alpha) = e(g^{p'},g) e ( gp,ga )=e ( gp′,g)
Note: There are also two problems exposed here,
- E ( α ) E(\alpha) in Proving KeyE ( α ) is public, that is to say, for Prover, he can break the polynomial restriction.
- A trusted third party is introduced, but in a more complex reality, it cannot be guaranteed that the third party is not malicious, such as not destroying the random secret of the trusted setup, which will lead to anyone can forge the proof once it is exposed.
So ZKSNARK introduces a multi-party joint setup, each with its own private key ( α , s ) (\alpha,s)( a ,s ) and the CRS generated by the previous person as input to generate a new CRS, as long as one person destroys the private key, the final CRS can be guaranteed to be safe. The specific implementation is as follows.it is only necessary to use homomorphic
multiplication to add everyone’s private key. )

( a ,s ) Perform random sampling and provide random numbers to be added to the CRS to achieve the purpose of destroying validity.
So how to verify the consistency of the final CRS? The previous Paring is used to
checksss : sets 1 s^1s1 as a benchmark, the verification method is as follows,
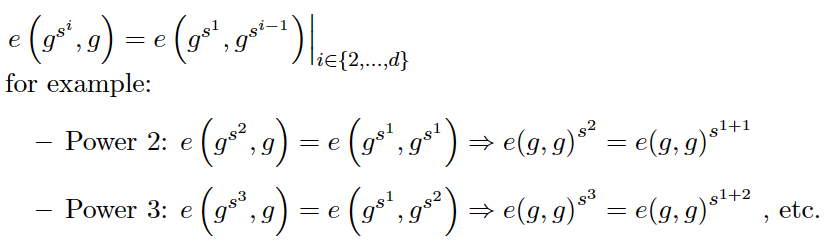
checkα − shift \alpha -shifta−s hi ft :
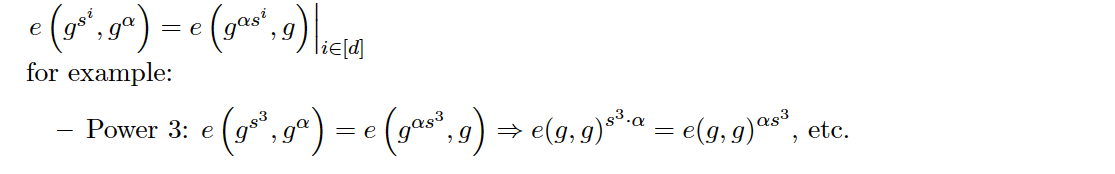
In order for participants to honestly use the CRS of other participants in front, each participant (except the first one) needs to be required to encrypt and disclose their own secret parameters, so that each participant can pass Paring Verify that other parties have done so honestly. As follows, suppose Bob exposes
( gs B i , g α B , g α B s B i ) ∣ i ∈ [ d ] \left.\left(g^{s_B^i},g^{\alpha_B},g^ {\alpha_Bs_B^i}\right)\right|_{i\in[d]}(gsBi,gaB,gaBsBi)
i∈[d]
Then the participant Alice can verify.
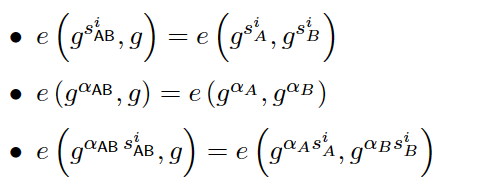
Similarly, the participant Carol can also verify after it is made public.
Complete short non-interactive polynomial proof scheme
这里用 { g s i } i ∈ [ d ] \{g^{s^i}\}_{i\in[d]} {
gsi}i∈[d]Represents s 1 , … , sds^1,\dots,s^ds1,…,sd
First determine the target polynomialt ( x ) t(x)t ( x ) and prover's polynomial degreeddd , the prover needs to prove that the polynomial he holds containst ( x ) t(x)t ( x ) .
details as follows

reference
A Brief Talk on Zero-Knowledge Proof: Background and Origin
zcash Official Popular Science
Exploring Elliptic Curve Pairings
Quadratic Arithmetic Programs: from Zero to Hero
Why and how zk-SNARK works
ZKSNARK introduces
Li Weihan, Zhang Zongyang, Zhou Zibo, etc. Summary of concise non-interactive zero-knowledge proof [J]. Journal of Cryptography, 2022, 9(03): 379-447. DOI: 10.13868/j.cnki.jcr.000525.