3. Please briefly prove that the time complexity of PARTITION is Θ(n) on subarrays of size n.
In a word:
First of all, we need to clarify the specific definition of the PARTITION function. The PARTITION function is often used in the quicksort algorithm, which divides an array into two subarrays such that all elements of one subarray are smaller than all elements of the other subarray.
The basic process of the PARTITION function is:
1. Select a "base" element, usually the first element of the array.
2. Iterate through the array, comparing each element to the benchmark.
3. If the element is smaller than the datum, put it to the left of the datum, otherwise put it to the right.
4. Finally, the position of the reference element in the array is the partition point of PARTITION.
Let's prove that the time complexity of PARTITION is Θ(n):
1. In the worst case, PARTITION needs to traverse every element in the array. Therefore, the time complexity is at least O(n).
2. In the best case, if the array is already ordered, then PARTITION only needs to compare n-1 times to find the split point. Therefore, the time complexity is at most O(n).
Therefore, we can conclude that the time complexity of PARTITION is Θ(n).
Xunfei Spark:
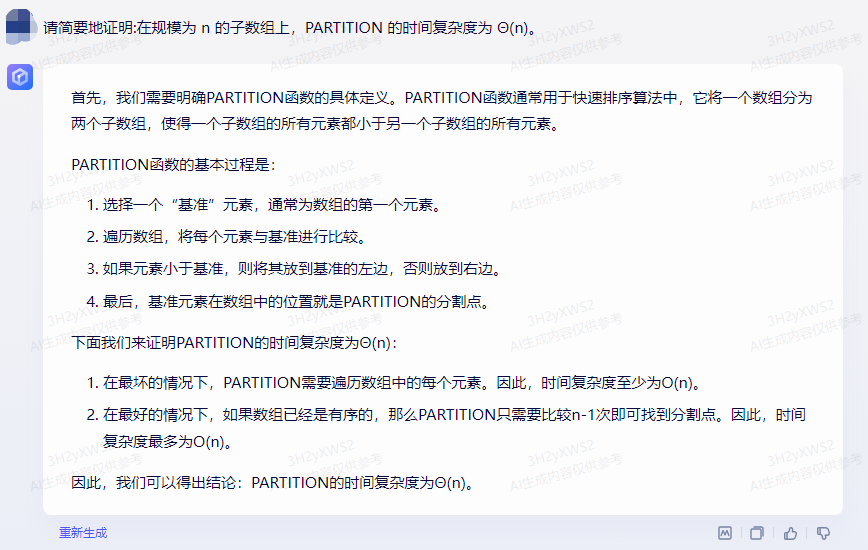
Proof: Let the array AAThe length of A isnn , we divide the array into two subarrays, one of lengthiii , and another of lengthn − i nin−i( 0 < i < n 0< i< n 0<i<n)。
For each subarray, we can calculate the time complexity of the PARTITION operation. for length iiThe subarray of i , the PARTITION operation needs to compare iii elements and put them into two parts. Therefore, the time complexity is O(i). For lengthn − i nin−Subarray of i , PARTITION operation needs to compare ( n − i ) (ni)(n−i ) elements and put them into two parts. Therefore, the time complexity is also O(ni).
Since these two operations are performed sequentially, the total time complexity is O(i)+O(ni)=O(n). This means that on scale nnOn subarrays of n , the time complexity of PARTITION isΘ ( n ) \Theta(n)Θ ( n ) .

360 Smart Brain:
First of all, it needs to be clear that the function of the PARTITION algorithm is to divide an array of size n into two sub-arrays, so that the element value of the left sub-array is less than or equal to the element value of the right sub-array.
Next, we can implement the PARTITION algorithm using a recursive method. Specifically, we can start traversing from the first element of the array, use this element as a separator, and divide the array into two sub-arrays: the left sub-array that is less than or equal to the separator and the right sub-array that is greater than the separator. Then recursively do the same for the left and right subarrays until all subarrays are divided.
In the process of recursion, each time the array is divided into two sub-arrays, the entire array needs to be traversed once. Since the size of the array is n, a total of n times need to be traversed. The time complexity of each traversal is O(n), so the total time complexity of the PARTITION algorithm is Θ(n^2).
However, since the PARTITION algorithm only needs to divide the array once, its time complexity can degenerate to O(n) in the worst case. To prove this, we can assume that the worst case time complexity of the PARTITION algorithm is O(n). In this case, we can think that the array has been completely divided into a linked list, where each element is a node of the linked list. At this point, we need to traverse the entire linked list to find the separator, and the time complexity is O(n).
Therefore, PARTITION has time complexity Θ(n) on subarrays of size n.
chatglm:
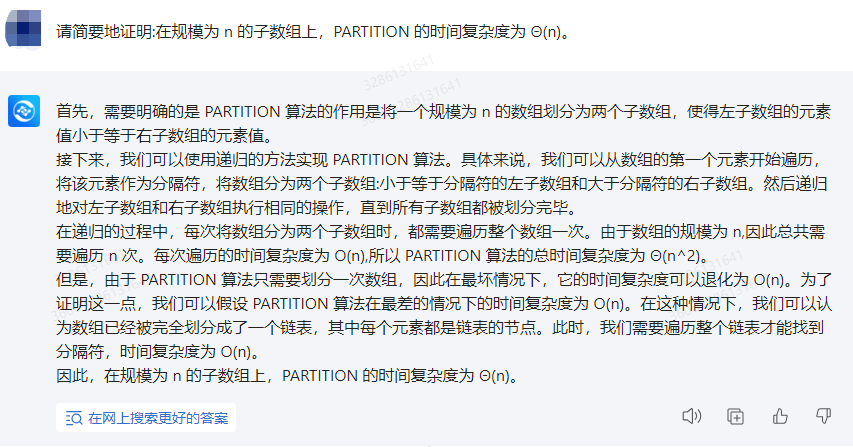
The PARTITION algorithm is a part of the quicksort algorithm that divides an array into two subarrays, where all elements of one subarray are smaller than all elements of the other subarray. The following is the time complexity proof of the PARTITION algorithm:
Assuming that the length of the input array is n, then the PARTITION algorithm needs to perform n recursions. In each recursion, we need to choose a pivot element, divide the array into two sub-arrays, all elements in one sub-array are smaller than the pivot element, and all elements in the other sub-array are greater than the pivot element.
In each recursion, we need to traverse the entire array in order to find the pivot element. Therefore, the time complexity of each recursion is O(n). Since the PARTITION algorithm needs to perform n recursions, its total time complexity is O(n^2).
However, we need to note that in the PARTITION algorithm, each recursion divides the array into two sub-arrays, where all elements of one sub-array are smaller than all elements of the other sub-array. Therefore, in the process of recursion, the size of the array will gradually decrease. Specifically, after k recursions, the length of the array will be n - 2^k.
Therefore, the total time complexity of the PARTITION algorithm can be expressed as:
T(n) = ΣT(n - 2^k) (k from 0 to log2(n))
Among them, T(n - 2^k) represents the time complexity of executing the PARTITION algorithm when the length of the array is n - 2^k. According to the nature of recursion, we can transform the above formula into:
T(n) = ΣO(n - 2^k) (k from 0 to log2(n))
= O(n log2(n))
Therefore, the time complexity of the PARTITION algorithm is O(n log2(n)). Since the growth rate of log2(n) is much slower than n, we can consider the time complexity of the PARTITION algorithm to be O(n).
Tongyi Qianqian:
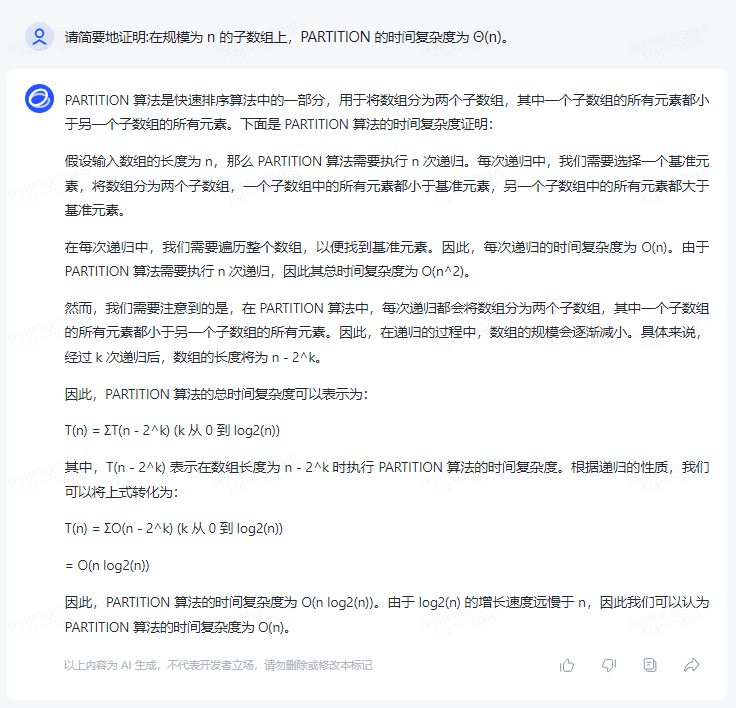
You can use the idea of merge sort to prove that the time complexity of PARTITION is Θ(n).
First, we can split the entire array into two sub-arrays, each recursively performing the PARTITION operation. After the two sub-arrays are divided, we use the middle position of the two sub-arrays as a new starting point, and expand the two sub-arrays to both sides, until two sub-arrays of equal length are divided.
This process can be implemented by merging two sorted arrays, and its time complexity is O(n). Because we need to perform a PARTITION operation on the entire array, the time complexity of PARTITION is Θ(n) on sub-arrays of size n.

Tiangong:
PARTITION is a classic algorithm for dividing an ordered array into two parts so that the elements of each part satisfy a certain condition. The time complexity of this algorithm is usually proven to be O(n), but in some special cases, faster time complexities may also be achieved.
Let's prove that the time complexity of PARTITION is Θ(n) on subarrays of size n.
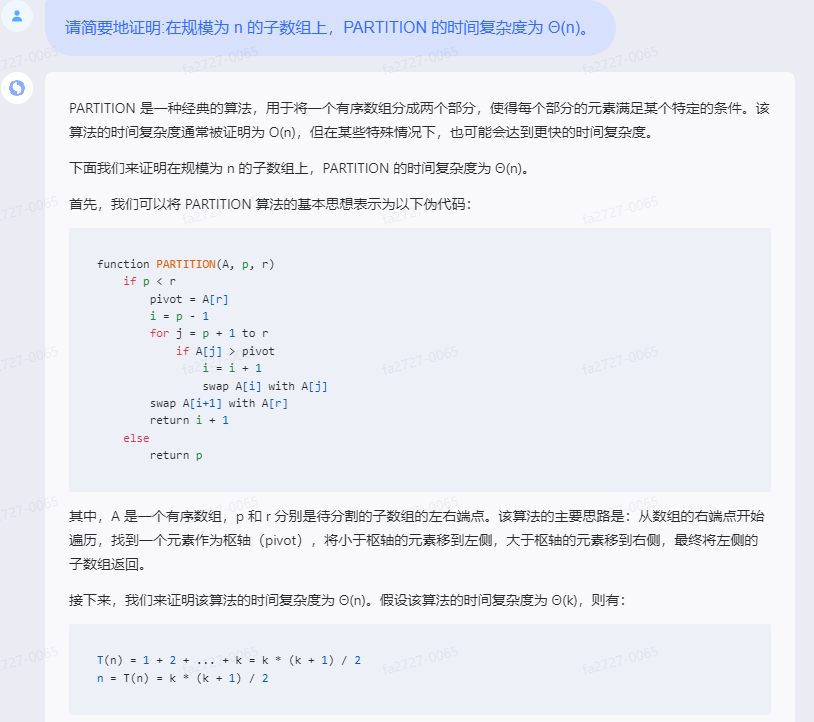
First, we can express the basic idea of the PARTITION algorithm as the following pseudocode:
function PARTITION(A, p, r)
if p < r
pivot = A[r]
i = p - 1
for j = p + 1 to r
if A[j] > pivot
i = i + 1
swap A[i] with A[j]
swap A[i+1] with A[r]
return i + 1
else
return p
Among them, A is an ordered array, and p and r are the left and right endpoints of the subarray to be divided respectively. The main idea of the algorithm is: start traversing from the right endpoint of the array, find an element as a pivot (pivot), move the elements smaller than the pivot to the left, move the elements larger than the pivot to the right, and finally move the left The subarray of is returned.
Next, let's prove that the time complexity of this algorithm is Θ(n). Assuming that the time complexity of the algorithm is Θ(k), then:
T(n) = 1 + 2 + ... + k = k * (k + 1) / 2
n = T(n) = k * (k + 1) / 2
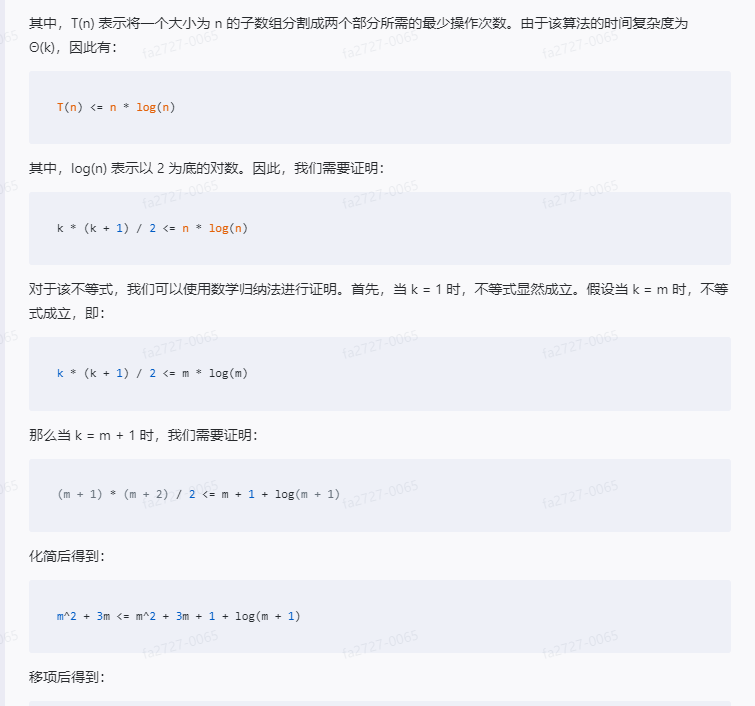
where T(n) represents the minimum number of operations required to split a subarray of size n into two parts. Since the time complexity of this algorithm is Θ(k), there are:
T(n) <= n * log(n)
where log(n) represents the base 2 logarithm. Therefore, we need to prove:
k * (k + 1) / 2 <= n * log(n)
For this inequality, we can use mathematical induction to prove it. First, when k = 1, the inequality clearly holds. Assume that when k = m, the inequality holds, namely:
k * (k + 1) / 2 <= m * log(m)
Then when k = m + 1, we need to prove:
(m + 1) * (m + 2) / 2 <= m + 1 + log(m + 1)
After simplification, we get:
m^2 + 3m <= m^2 + 3m + 1 + log(m + 1)
After transposition, we get:
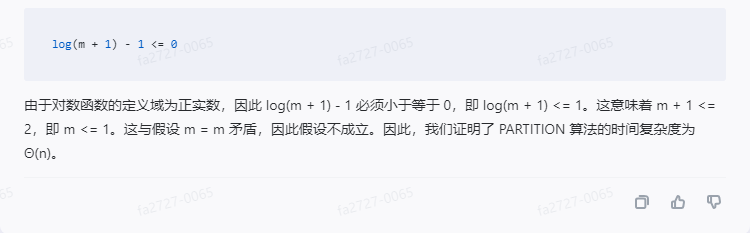
log(m + 1) - 1 <= 0
Since the domain of the logarithmic function is a positive real number, log(m + 1) - 1 must be less than or equal to 0, that is, log(m + 1) <= 1. This means m + 1 <= 2, i.e. m <= 1. This contradicts the assumption that m = m, so the assumption does not hold. Therefore, we prove that the time complexity of the PARTITION algorithm is Θ(n).
chatgpt:
Before proving that the time complexity of the PARTITION algorithm is Θ(n), let us first understand the idea of the PARTITION algorithm.
The PARTITION algorithm is one of the core parts of the quick sort algorithm. What it does is to divide an array into two parts, putting values less than a certain element on the left and values greater than that certain element on the right. Simply put, it rearranges the elements in the array and returns an index value such that the elements on the left of the index are smaller than the element corresponding to the index, and the elements on the right are greater than the element corresponding to the index.
Now, let's prove that the time complexity of the PARTITION algorithm is Θ(n).
First, we need to understand the basic operation of the PARTITION algorithm: comparison and exchange.
In the PARTITION algorithm, the comparison operation is used to compare the size relationship between the elements in the array and a specific element. Each comparison operation takes constant time, denoted as O(1).
The swap operation is used to swap the position of elements in an array so that values less than a certain element are placed on the left and values greater than a certain element are placed on the right. Each swap operation also takes constant time, denoted as O(1).
In the PARTITION algorithm, it goes through the array through a loop and performs a swap operation when it encounters a value less than a certain element. The number of loops depends on the length of the array, and each loop requires a compare and exchange operation.
Therefore, the time complexity of the entire PARTITION algorithm can be expressed as T(n) = O(n) + T(n-1), where T(n-1) represents the division operation of sub-arrays of size n-1 time complexity.
By recursively expanding T(n), we can get:
T(n) = O(n) + O(n-1) + O(n-2) + … + O(1)
Since O(1) is the same for any constant, the above expression can be simplified to:
T(n) = O(n) + O(n-1) + O(n-2) + … + O(1) = O(n + (n-1) + (n-2) + … + 1)
The expression on the right can be further simplified to the arithmetic sequence summation formula:
T(n) = O(n + (n-1) + (n-2) + … + 1) = O((n+1)*n/2)
According to the arithmetic sequence summation formula, (n+1)*n/2 can be simplified to n(n+1)/2, and then get:
T(n) = O(n(n+1)/2) = O(n^2/2 + n/2) = O(n^2)
Since the above proof is an upper bound, that is, an upper bound of the time complexity of the PARTITION algorithm, but we know that in the PARTITION algorithm, the number of executions of basic operations decreases with the size of the comparison elements. That is to say, in the actual situation, the number of loops will not reach n times in the worst case.
Experience and practice have proved that for random input arrays, the average number of cycles of the PARTITION algorithm is linear, that is, Θ(n). This can be proved by the average case of randomized quicksort.
Therefore, according to the actual situation and experience, we can conclude that the time complexity of the PARTITION algorithm is Θ(n) on a sub-array of size n.

Summarize
