Dynamic programming is an important point in the algorithm. The first time I encountered it was in the degree course "Algorithm Design and Analysis" in the second semester of my sophomore year. But at that time, I just learned very shallowly to cope with the school's final exam. I saw a video about the dynamic programming algorithm on the website, and learned the dynamic programming again, so I wrote this article to record the re-learning of the dynamic programming algorithm.

analyze:

Recursion:

Why mention recursion here? In fact, there is a connection between the recursive algorithm and the dynamic programming algorithm, which we will clarify later when we analyze the recursive implementation of the Fibonacci sequence.

In my previous article C Language - August 1 - Recursion and Dynamic Memory Management, I wrote about recursion. Here is the definition of recursion again:

The programming technique that the program calls itself is called recursion (Recursion)

I personally think that recursion is also a programming skill with great mathematical thinking, because the process of recursion includes decomposing a complex problem into multiple smaller-scale problems, and merging problems of equal size into the original problem size after the decomposition is completed the process of. In the previous article, I used recursive techniques to realize mathematical problems such as Fibonacci sequence, Yanghui triangle, Joseph ring, etc., and recursion is also the same in the three mainstream methods (one-dimensional array, two-dimensional array, recursion) of Yanghui triangle. The one that takes up the least amount of memory and is the most efficient. Well, without further ado, let's analyze the Fibonacci sequence.

Recursive Fibonacci Sequence (Fibonnaci Sequence):

The Fibonacci sequence has been implemented using recursive techniques and analyzed the process of function calls in the previous article. Here is the code and tree diagram:

Recursive function for the Fibonacci sequence:

int Fibonnaci(int n)
{
    if(n == 1 || n == 2){//递归出口
        return 1;
    }
    else{
        return Fibonnaci(n - 1) + Fibonnaci(n - 2);//递归核心语句，除了第一个和第二个值任何一个值都等于它前面两个值相加的总和
    }
}

Analysis dendrogram of recursive form of Fibonacci sequence:

In this picture we can see that we are asking for the sixth number in the Fibonacci sequence. We decompose the required sixth number into asking for the fifth number and the fourth number, and then respectively Decompose finding the fifth number and finding the fourth number into finding the fourth number and the third number and finding the third number and the second number. The second number and the first number are actually the recursive exit 1, so at this time the third number is 2, the fourth number is 3, the fifth number is 5, the sixth number is 8, and the number 8 is the final result.

But in this tree diagram, we have performed an extremely memory-consuming behavior - function call.

As shown in the figure, for example, on the premise that we have obtained Fibo(4) through the subtree under the left subtree Fibo(4) of the third layer, we need to perform another calculation through the call under the right subtree of the second layer value, that is to say, the size of the tree will be doubled every time the required value grows, so the time complexity of this program based on the recursive Fibonacci sequence in this way is terrible O(2^n).

The connection between recursion and dynamic programming (Recursion and Dynamic Programming):

Above we have analyzed the solution method of the recursive Fibonacci sequence in the normal state, but because the time complexity of this method is too large, we introduce a new knowledge point: Overlap sub-problem (Overlap sub-problem ) )

Overlap sub-problem

In the dendrogram of the Fibonacci sequence solution, we need to make multiple and repeated function calls, and the number of calls is exponentially increasing, but if we save the value calculated each time and directly To call, for example, we need to continue to follow the sixth tree of the Fibonacci sequence. On the premise that the fourth number and the fifth tree have been calculated, we can use it directly, and the complexity will be much simpler. And it can speed up the entire calculation process. Here is a picture to draw a picture and let's take a look at the process:

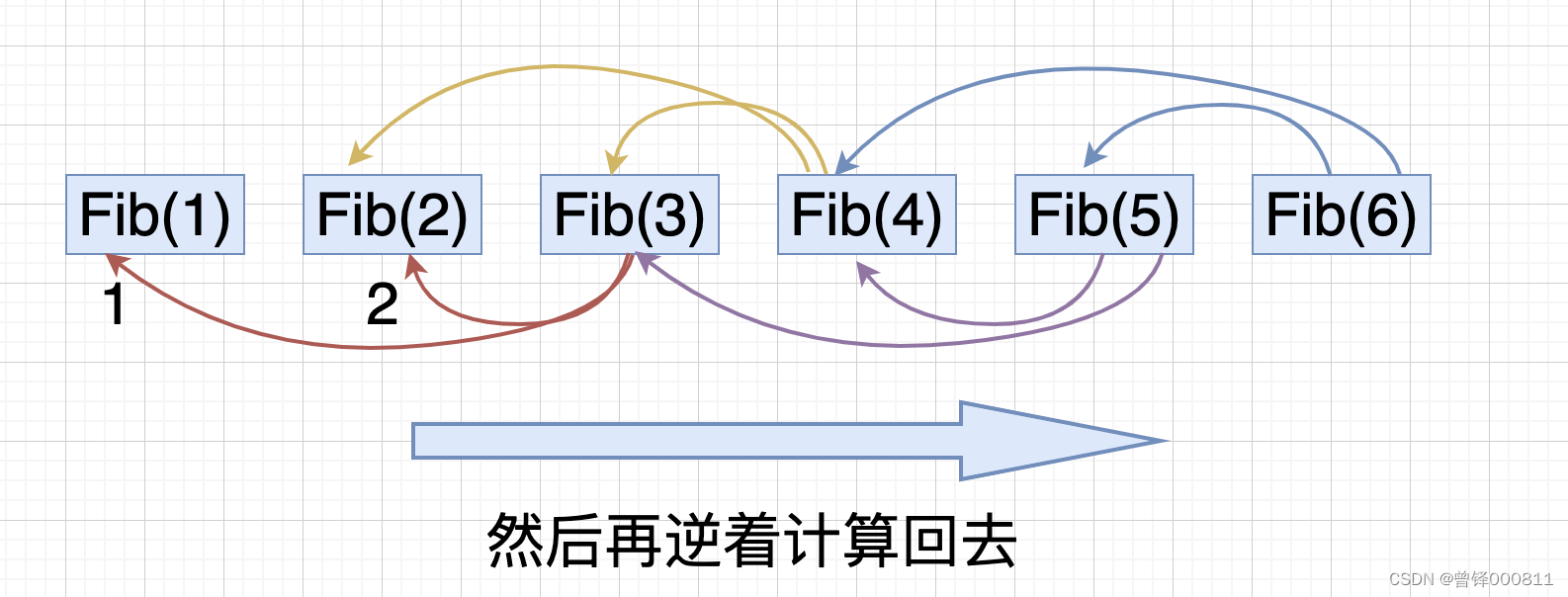
At this time, the time complexity of the program becomes: O(n)

In fact, the overlapping sub-problem (Overlap sub-problem) is the idea to be used in dynamic programming later.

Dynamic Programming:

In Wang Xiaodong's "Algorithm Design and Analysis", the introduction of dynamic programming is as follows: the dynamic programming algorithm is similar to the divide and conquer method. The solution to the subproblem yields the solution to the original problem.

The dynamic programming algorithm is suitable for solving optimization problems, and the dynamic programming algorithm can usually be designed according to the following steps:

(1) Find out the properties of the optimal solution and characterize its structural characteristics.

(2) Recursively define the optimal value

(3) Calculate the optimal value in a bottom-up manner

(4) According to the information obtained when calculating the optimal solution, construct the optimal solution

We understand these four steps through the following two examples:

Dynamic programming optimal solution problem:

Problem Description:

At this time, we need to work outside to earn money. The figure below shows the remuneration we can get for working in different time periods. For example, the remuneration we can get when we choose job 1 is 5 yuan, but after we choose job 1, we cannot because of time conflicts. Choose job 2 or job 3 and so on, we now have to figure out how to arrange today's work to maximize the benefits we can get, and find the optimal solution:

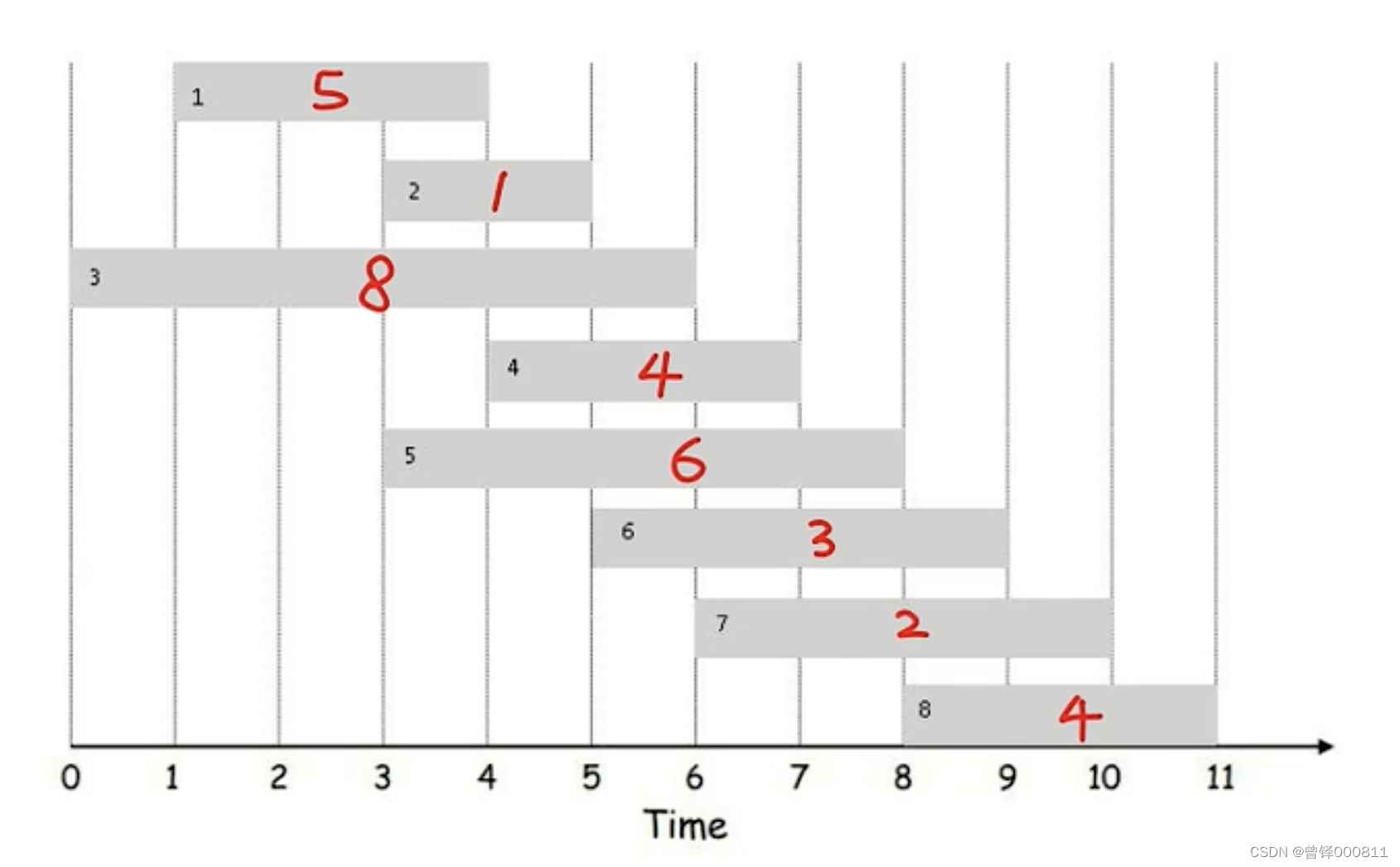
problem analysis:

In this topic, a choice problem is involved, that is, to choose or not to choose the work in this time period

At this time, the three parameters are set to be Opt, Prev, and V. The meanings of the first two correspond to the words optimize (optimize) and previous (previous). Opt selects the optimal value, and Prev represents the optimal value before this selection . Choice, V represents the value corresponding to this choice.

Here's an example to give us a quick jump in:

For example, I am aiming at job 8 for the first time here, and we have two choices, that is, to choose job 8 and not to choose job 8, which can be expressed as follows:

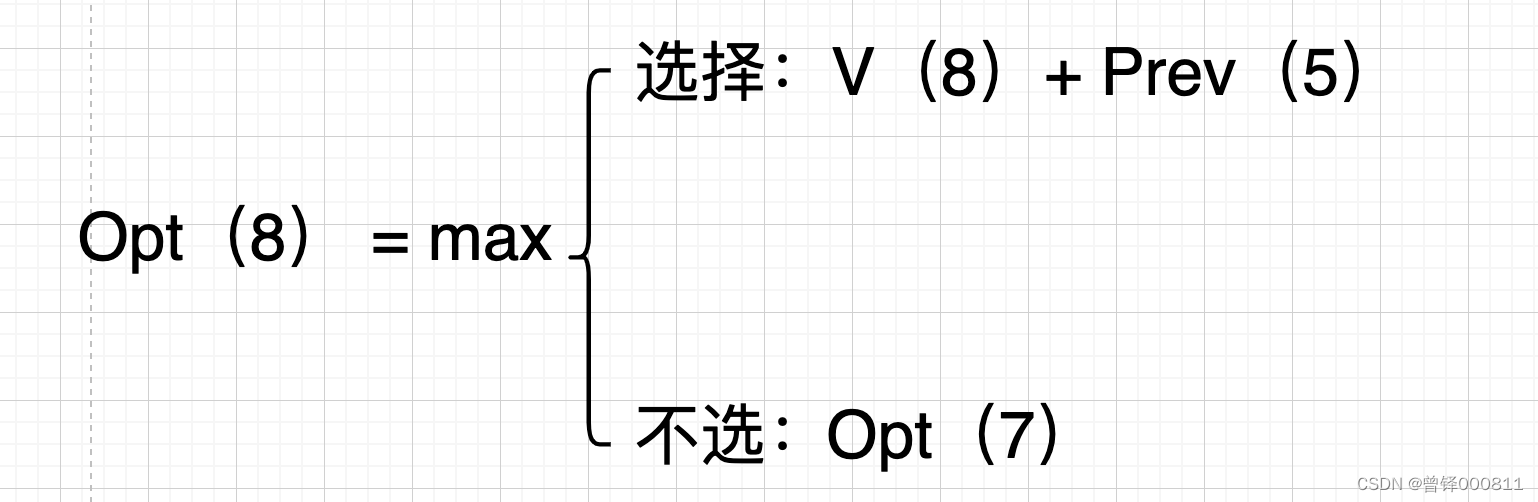
If we choose job 8, we have to find the optimal value in the first 5 jobs and add the benefits that job 8 can generate. If we don’t choose, we will directly find the optimal value in the first 7 jobs . Let’s first draw a picture to clarify the relationship between Prev and Opt:

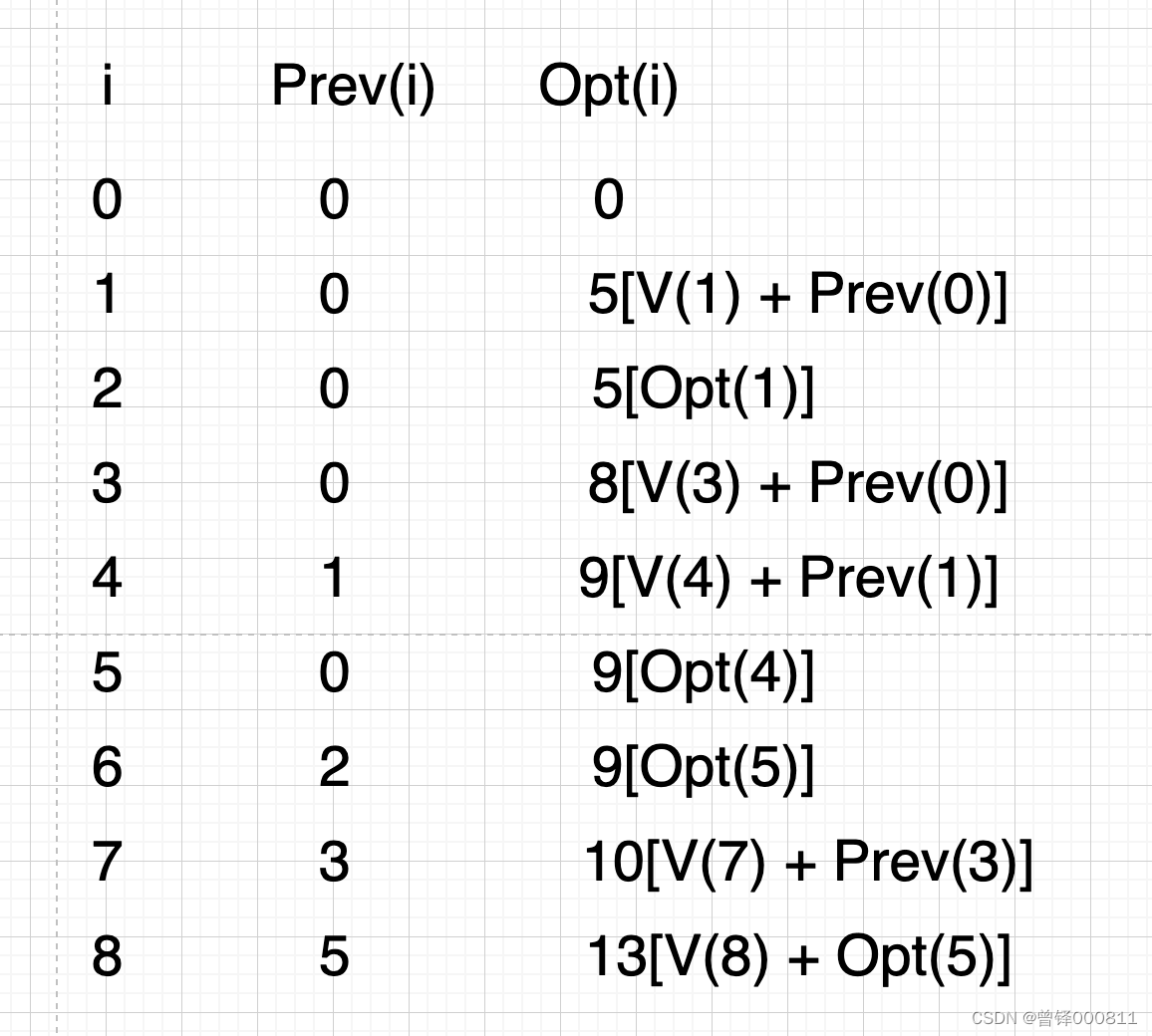
We understand this picture like this:

When traversing to job 1, the maximum benefit that can be generated is to only do job 1, and the benefit is 5;

When traversing to job 2, the maximum benefit that can be generated is to only do job 2, and the benefit is 1;

When traversing to job 3, the maximum income that can be generated is to only do job 3, and the income is 8;

When traversing to work 4, the maximum income that can be generated is to do work 4 and then work 1, and the income is 9;

When traversing to job 5, the maximum benefit that can be generated is not to choose job 5 but to choose the optimal result of traversing to job 4 before, and the benefit is 9;

When traversing to job 6, the maximum benefit that can be generated is not to choose job 6 but to choose the optimal result of traversing to job 5 before, and the benefit is 9;

When traversing to job 7, the maximum income that can be generated is the optimal result when selecting job 7 and then traversing to job 3, and the income is 10;

When traversing to job 8, the maximum benefit that can be generated is the optimal result when selecting job 8 and then traversing to job 5. As mentioned earlier, the optimal result of traversing to job 5 is to select job 4 and then choose job 1, so the job 1, job 4, and job 8 are done separately, and the income is 13;

In summary, the optimal solution to this problem is 13. This is to find the optimal value from the bottom up.

Sum of non-adjacent numbers and maximum problem:

Problem Description:

Among several numbers stored in the array, we need to find numbers that are not adjacent to each other to maximize their sum, and there are several choices for several numbers, for example, I give 7 numbers here Stored in the array of subscripts 0-6, respectively:

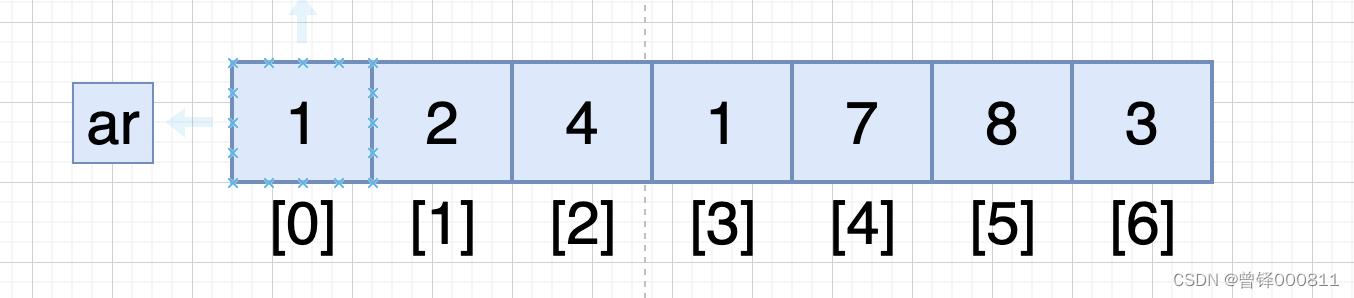
If I select element 4 at this time, his non-adjacent elements at this time are element 1 with subscript 0, element 7 with subscript 4, and element 3 with subscript 6.

All we have to do now is to ask for the maximum value of the sum of non-adjacent elements that exist in this sequence, and it depends on which one we choose.

problem analysis:

First, we set two formal parameters, namely OPT, i, where i represents the number of elements, and OPT is used to represent the maximum sum of the first element to the i-th element.

When traversing to element 1, the value of i is 1 at this time, which is OPT(1). Since there is only one element, the optimal choice can only be 1, and the value returned is the value of ar[0] itself.

When traversing to element 2, the value of i is 2 at this time, which is OPT(2). Because there are two elements, they cannot be adjacent to each other, so either choose the first one or the second one, and use the formula to express That is: ar[0] > ar[1] ? ar[0] : ar[1];

When traversing to element 3, the value of i at this time is 3, that is, OPT (3). Now we have two options, one is that we choose element 3, and after selecting element 3, there is element 1 that is not adjacent to element 3. Expressed in a formula: OPT(3) = OPT(1) + ar[2] ; the other is that we choose element 2, because element 2 has no non-adjacent elements, and what is returned is the value of element 2 itself Now, that is ar[1] ;

When traversing element 4, the value of i at this time is 4, that is, OPT (4). Now there are still two choices. One is that we choose element 4, and there are 2 elements that are not adjacent to element 4. Use the formula The expression is: OPT(4) = OPT(2) = ar[3] ; the other is that we select the previous element of element 4, element 3, and element 3 has a non-adjacent element when element 1, Expressed in the formula that is: OPT(3) = OPT(1) + ar[2] ;

When traversing to element 5, the value of i at this time is 5, which is OPT(5). Now if we choose element 5, we can use the formula to express: OPT(5) = OPT(3) + ar[ 4 ] , OPT(3) appeared at this time, we have discussed before, this is the Overlap subproblem, so we can directly substitute OPT(3) into the formula, so the value of OPT(5) is 12 . When we do not choose element 5 but choose element 4 before 5, then the formula becomes OPT(4) = OPT(2)+ ar[3] , we have also discussed OPT(2) before, continue Substitute, at this time OPT(4) = 3; obviously OPT(5) > OPT(4), so the optimal choice at this time is OPT(5), with a value of 12 .

When traversing to element 6, the value of i is 6 at this time. There are also two choices. Selecting element 6 is expressed by the formula: OPT(6) = OPT(4) + ar[5] , if we do not select the element 6 turns to select the element 5 before 6, which is expressed by the formula OPT(5) = OPT(3) + ar[4] , the value of OPT(5) has been calculated before as 12, and the value of OPT(4) is 3 , so the value of OPT(6) is 3+8=11, and OPT(5) > OPT(6), so the optimal choice at this time is OPT(5), with a value of 12 .

When traversing to element 7, the value of i is 7 at this time. There are also two options. Selecting element 7 is expressed by the formula: OPT(7) = OPT(5) + ar[6] , if we do not select the element 7 turns to select the element 6 before 7, expressed by the formula is OPT(6) = OPT(4) + ar[5] , the value of OPT(6) has been calculated before 12, the value of OPT(5) is 12, so the value of OPT(7) is 12 + 3 = 15, OPT(7)>OPT(6), so the optimal choice at this time is OPT(5), the value is 15, which is also the final solution of this question .

Analysis in dendrogram form:

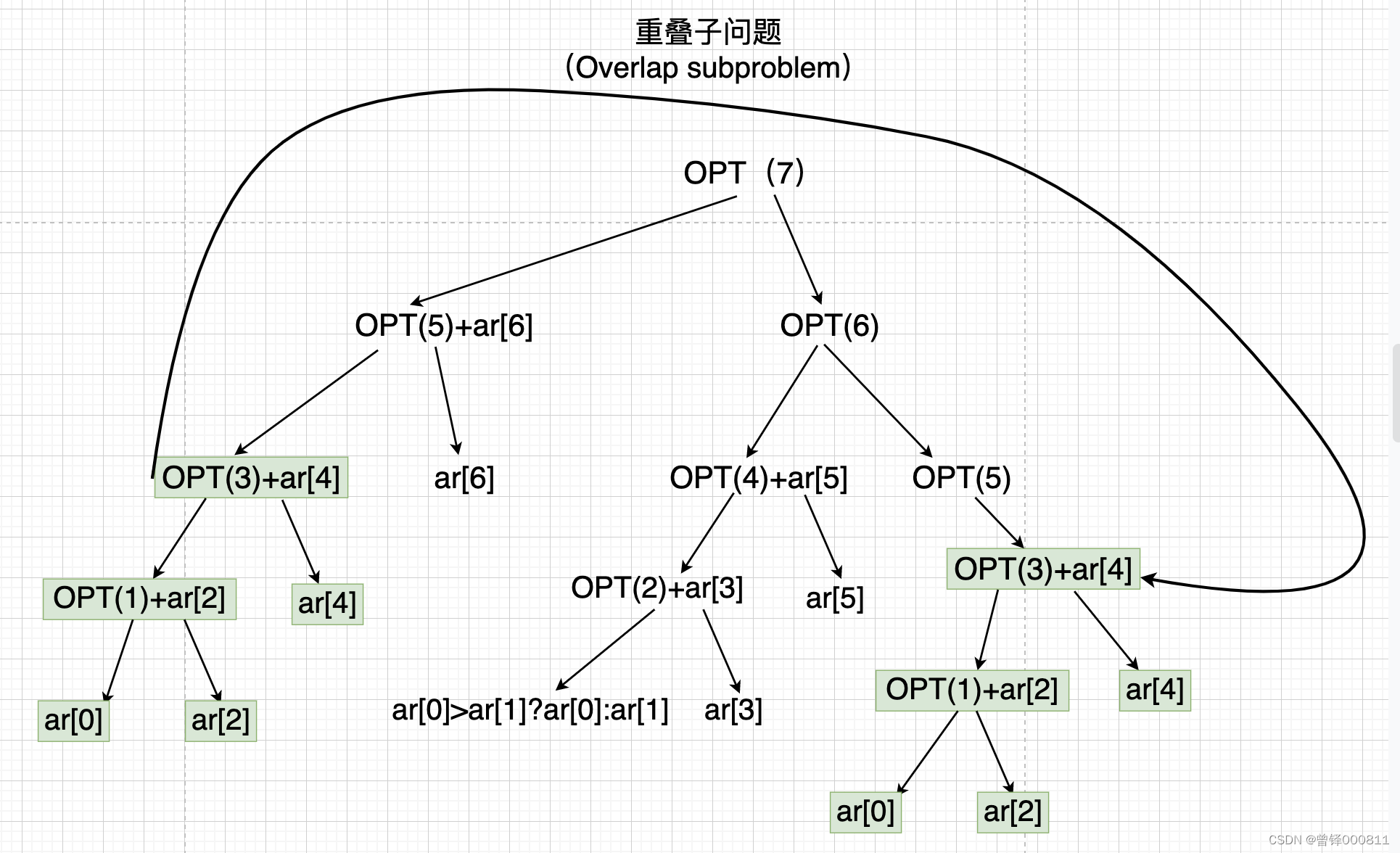
The expressions enclosed by the green boxes in the figure are overlapping subproblems, which can be substituted into each other through the memory function to effectively reduce the time complexity of recursion.

Analysis in tabular form:

Note: The blue box corresponds to the maximum sum value from the first to the i-th element traversed as the number of traversed elements increases. The same value represents overlapping sub-problems, which can be substituted for each other to reduce the time complexity of the program.

Law summary:

At this point, we have basically understood the analysis process, and now write the analyzed law into an equation:

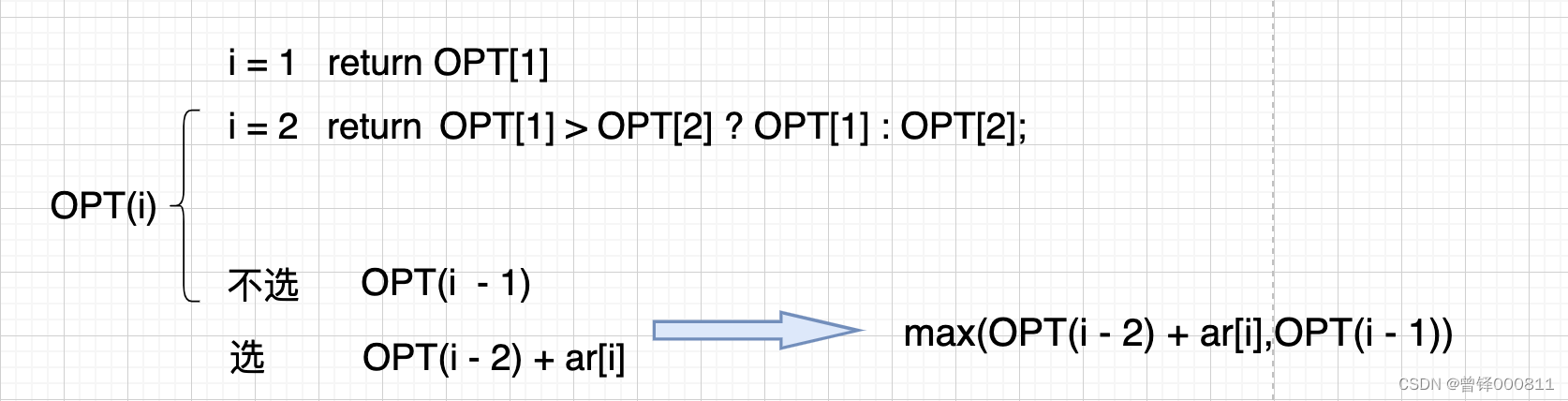
Note: The two i in OPT(i - 2) and ar[i] are different! The former indicates the number of elements, and the latter indicates the subscript of the elements in the array.

Code implementation (recursive method):

//动态规划（不相邻数字最大和问题）
#include<cstdio>
#include<cassert>
#include<cstdlib>
int Recursion_OPT(int *ar,int i)//递归方法
{
    assert(ar != NULL);
    if(i == 0){//讨论当选择第一个元素的情况
        return ar[0];
    }
    else if(i == 1){//讨论当选择第二个元素的情况
        return ar[0] > ar[1] ? ar[0] : ar[1];
    }
    else{//讨论其他元素的情况
        int a = Recursion_OPT(ar,i - 2) + ar[i];
        int b = Recursion_OPT(ar,i - 1);
        return a > b ? a : b;//在两种情况中选择最大值
    }
}
int main()
{
    int ar[7] = {1,2,4,1,7,8,3};
    printf("result = %d\n",Recursion_OPT(ar,7));//调用函数
    return 0;
}

operation result:

Code implementation: dynamic programming (overlapping sub-problem memory function)

//动态规划（不相邻数字最大和问题）
#include<cstdio>
#include<cassert>
#include<cstdlib>
int DP_OPT(int *ar,int i)//动态规划方法（优化重叠子问题方式）
{
    int *p = (int *)calloc(7, sizeof(int));//在堆区申请7个int类型的空间并全部初始化为0
    if (i == 0) {//当选择第一个元素时，直接返回ar[0]的值
        return ar[0];
    } else if (i == 1) {//选择第二个元素的值时，返回ar[0]和ar[1]中较大的值
        return ar[0] > ar[1] ? ar[0] : ar[1];
    }
    p[0] = ar[0];//将数组中的值复制给堆区申请的int类型空间（已初始化为0）
    p[1] = ar[0] > ar[1] ? ar[0] : ar[1];
    for (int j = 2; j <= 6; j++) {//讨论其他元素
        int a = p[j - 2] + ar[j];//方程思想
        int b = p[j - 1];
        p[j] = a > b ? a : b;
    }
    return p[6];
}
int main()
{
    int ar[7] = {1,2,4,1,7,8,3};
    printf("result = %d\n",DP_OPT(ar,7));
    return 0;
}

operation result:

Comparison of the two methods:

The first method is a recursive method, which does not make good use of overlapping sub-problems, the cost of space is very high, and the time complexity is: O(2(^n));

The second method is a dynamic programming algorithm, which uses overlapping sub-problems and substitutes each other, effectively reducing the time complexity to O(n).

References:

Lighting Lanterns on the First Moon - Lecture 1 of Dynamic Programming https://www.bilibili.com/video/BV18x411V7fm?spm_id_from=333.880.my_history.page.click&vd_source=c121339fd44664a8ecff62ce46a4724d

Lighting Lanterns on the First Moon - Dynamic Programming (Dynamic Programming) Lecture 2 https://www.bilibili.com/video/BV12W411v7rd/?spm_id_from=333.337.search-card.all.click&vd_source=c121339fd44664a8ecff62ce46a4724d

Algorithms - Introduction to Dynamic Programming (Dynamic Programming)

introduction:

analyze:

Recursion:

Recursive Fibonacci Sequence (Fibonnaci Sequence):

Recursive function for the Fibonacci sequence:

Analysis dendrogram of recursive form of Fibonacci sequence:

The connection between recursion and dynamic programming (Recursion and Dynamic Programming):

Overlap sub-problem

Dynamic Programming:

Dynamic programming optimal solution problem:

Problem Description:

problem analysis:

Sum of non-adjacent numbers and maximum problem:

Problem Description:

problem analysis:

Analysis in dendrogram form:

Analysis in tabular form:

Law summary:

Code implementation (recursive method):

operation result:

Code implementation: dynamic programming (overlapping sub-problem memory function)

operation result:

Comparison of the two methods:

References:

Guess you like