Sword refers to the subsequent traversal of offer33 binary search tree

Sword refers to offer 33. Subsequent traversal of binary search tree

Title description:

Input an integer array, and judge whether the array is the post-order traversal result of a certain binary search tree. Returns true if yes, false otherwise. Assume that any two numbers in the input array are different from each other.

example

Consider the following binary tree:

示例1
输入：[1,6,3,2,5]
输出：false
示例2
输入：[1,3,2,6,5]
输出：true

Problem-solving ideas:

• According to the binary tree post-order traversal sequence "left, right, middle", the array is divided [left | right | root].
• The definition of binary search tree: the value of all nodes of the left subtree is less than the value of the root node, the value of the left and right nodes of the right subtree is greater than the value of the root node, and the left and right subtrees are also search trees.
  

Method 1: Recursion, divide and conquer

train of thought

• According to the definition of binary search tree, through recursive traversal, judge the correctness of all subtrees, and
  recursively parse:

• Termination condition: when $i>=j$ , indicating that the number of nodes in this subtree is <= 1, no need to judge the correctness, directly return$true$，

• Recursive work:
  1. Divide the left and right subtrees: Traverse the [i, j] interval elements of the subsequent traversal from left to right, find the first element greater than the root node, and record the index as $m$ . At this point, the left subtree interval$[i,m-1]$ , right subtree interval$[m,j-1]$ , the root node index is$j$ .
  2. Determine whether it is a binary search tree: (according to the definition of a binary search tree)

  • Left subtree interval $[i,m-1]$ all nodes within should be$<posterder\left[j\right]$ . In the first step, in the process of finding the first value index greater than the root node, the node value of the left subtree has been judged, so there is no need to re-comparison next.
  • Right subtree interval $[m,j-1]$ , all node values ​​inside should be $ > posterderp[]j$,Start\; traversing\; right\; fromindex$ m+1$, encounter the first$The\; value\; of\; posterder\left[j\right]$ , returns its index$p$ , judging that$p==j$ , if satisfied, this interval is a binary search tree.

• All subtrees need to be judged correctly before returning true; so use && logic symbols to connect:

1.$p==j$ , judge that the current interval subtree satisfies definition
2.$traversal(i,m-1)$ : Judge whether the left subtree of this tree is correct.
3.$traversal(m,j-1)$ : Judge whether the right subtree is correct.
Returns true only when all three are true.

code snippet

class Solution{
    
    
public:
	bool traversal(vector<int>& posterder,int i,int j){
    
    
		if(i >= j) return true;
		int p = i;
		while(posterder[p] < posterder[j]) p++;
		int  m = p;
		while(posterder[p] > posterder[j]) p++;
		return (p==j) && traversal(posterder,i,m-1) && traversal(posterder,m,j-1);
	}
	bool verifyPosterder(vector<int>& posterder){
    
    
		if(posterder.size() <= 1) return true;
		return traversal(posterder,0,posterder.size()-1);
	}
}

Complexity Analysis

• Time complexity: $O\left(N^2\right)$: Each call to recursion subtracts one root node, so recursion takes$O\left(N\right)$ ; In the worst case, when the tree degenerates into a linked list, each round of recursion needs to traverse all the nodes of the tree, occupying$O\left(N\right)$ .
• Space complexity $O\left(N\right)$ : In the worst case, when the tree degenerates into a linked list, the recursion depth reaches$N$。

Method 2: Monotonic stack

train of thought

• This method traverses the array backwards, i.e. [root|right|left].

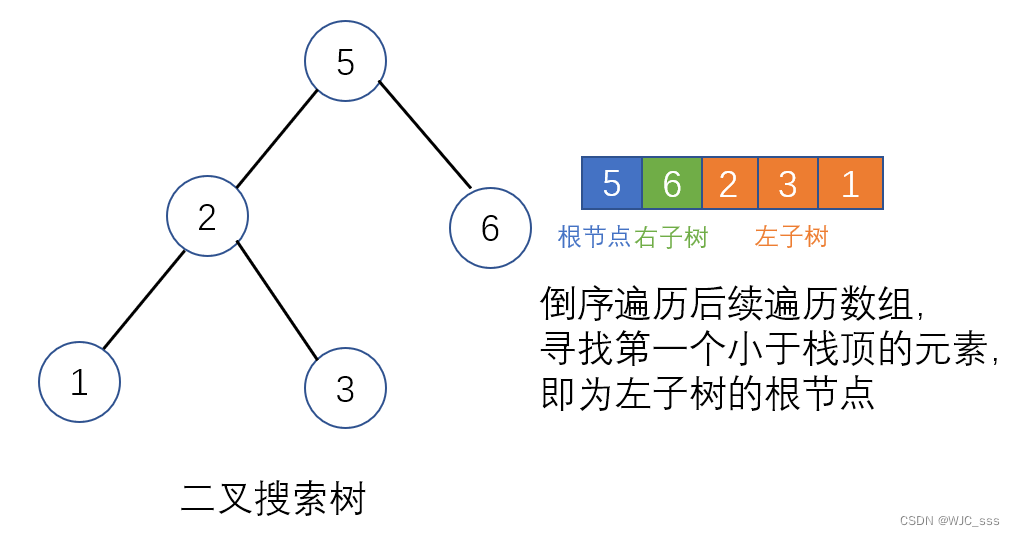
• Set the subsequent traversal in reverse order $[r_n,r_{n-1},...r_1]$ , traverse the list, set the index to$i$ , if it is a binary search tree, there are:

  • When the node value $r_i>r_{i+1}$When: node value $r_i$Must be node $r_{i+1}$the right child node of .
  • When the node value $r_i<r_{i+1}$When: node value $r_i$It must be the left child node of root, and root is the node value $r_{i+1},r_{i+2},....r_n$The value in is greater than and closest $r_i$of nodes.

• 对于$r_i<r_{i+1}$, if it is a binary search tree, then $r_i$All nodes on the right $[r_{i-1},r_{i-2},...r_1]<root$。

• According to the above characteristics, use a monotonic stack as an auxiliary:
  1. With the help of a monotonic stack $stack$ store the node whose value increases;
  2. When encountering an order with decreasing value$ri$$r_i$, update ri r_i by popping the stack$r_i$The parent node $root$ ;
  3. Each round of judgment$r_i$sum root rootThe value relationship of$r$$o$$o$$t$
  : (1) If$r_i>root$ , it does not satisfy the definition of binary tree, return false;
  (2) If$r_i<root$ , continue to traverse.

Algorithm process

1. Initialization: monotone stack stack, the initial root node is $root=+\infty$ . (Think of the root node of the tree as the left child of this infinite node);
2. Traverse$posterder$ record each node as$r_i$；

• Judgment，$r_i>root$ does not meet the definition of binary search tree, return false;
• Update the parent node $root$ : when the stack is not empty, and$r_i<When\; stack.top\left(\right)$ , the pop-up is executed cyclically, and the pop-up node is assigned to$root$。
• Push into the stack: put the current node $r_i$into the stack.

3. The traversal is complete and returns true;

Complexity Analysis

• Time complexity $O(N$ : traverse$posterder$ all nodes, each node is pushed into the stack,/popped once, using$O\left(N\right)$ time.
• Space complexity $O\left(N\right)$ : worst case, monotonic$stckstores$ all incoming orders$.$Use$O\left(N\right)$ extra space.

code snippet

class Solution{
    
    
public:
    bool verifyPostorder(vector<int> & postorder){
    
    
        stack<int> st;
		int root = INT_MAX;
		for (int i = postorder.size()-1;i >= 0;i--){
    
    
			if (postorder[i] > root) return false;
			while(!st.empty() && st.top() > postorder[i]){
    
    
				root = st.top();
				st.pop();
			}
			st.push(postorder[i]);
		}
		return true;
    }
};