Represent rotation with Quaternion or DCM Matrix

English reference link: Quaternions

DCM Tutorial – An Introduction to Orientation Kinematics – Starlino Electronics

https://ntrs.nasa.gov/api/citations/19770024290/downloads/19770024290.pdf

Quaternions, which are a generalization of complex numbers represented by four real numbers, can be used to efficiently represent and compute rotations in three-dimensional space1 .

DCM matrix

DCM matrix is a matrix used to describe the transformation between two coordinate systems. If we record the first coordinate system as x and the second coordinate system as y, then the DCM matrix is a 3x3 matrix, and each column of it is the representation of a unit vector of the y coordinate system in the x coordinate system.

$DCM^{B} = (DCM^G)^T$ or $DCM^G = (DCM^B)^T$

and

The DCM matrix (also often referred to as the rotation matrix) defines the rotation of one frame relative to another. It can also be used to determine the coordinates of an arbitrary vector in the global frame if we know the coordinates of the arbitrary vector in the B frame (and vice versa).

a vector with body coordinates:

If we know the rotation angle between two coordinate systems, such as yaw angle (yaw), pitch angle (pitch) and roll angle (roll), then we can use some mathematical formulas to calculate the DCM matrix. These formulas depend on the order of the rotations, such as first rotating the yaw angle around the z-axis, then the pitch angle around the y-axis, and finally the roll angle around the x-axis. This order can be denoted as ZYX. Then the corresponding DCM matrix can be written as

The difference between intrinsic rotation and extrinsic rotation is that the former refers to the rotation around the axis of the rotated coordinate system, and the latter refers to the rotation around the axis of the fixed coordinate system. For example, if we use the ZYX order to represent rotation, then intrinsic rotation is to first rotate the roll angle (roll) around the x-axis, then rotate the pitch angle (pitch) around the new y-axis (y′), and finally around the new The z-axis (z″) rotates the yaw angle (yaw). The extrinsic rotation is to first rotate the yaw angle around the z-axis, then rotate the pitch angle around the original y-axis, and finally rotate the roll angle around the original x-axis.

Quaternion

Properties of rotation quaternions:

All rotation quaternions must be unit quaternions.|q| = 1
For rotation quaternions, the inverse equals the conjugate. So for rotation quaternions, q−1 = q* = ( q0, −q1, −q2, −q3 ).
If a point p is turned into p' after being rotated by q, then it will be changed back to p by rotating p' by q−1 or q*. This is because the two rotations cancel each other out
A rotation of qa followed by a rotation of qb can be combined into the single rotation qc = qbqa.

Convert quaternion to rotation matrix

Convert rotation matrix to quaternion

Convert Euler Angles to Quaternion

θ (theta) y
φ (phi) x
ψ (psi) z

agreement:

Intrinsic rotation (axis moves with each rotation)
Active (aka alibi) rotation (rotates the point, not the coordinate system)
Right-handed coordinate system with right-handed rotation

The quaternion q corresponding to the Euler angles z, x, and y in ZXY order is:

$R = R_{z}(\theta_{z})R_{x}(\theta_{x})R_{y}(\theta_{y}) = \begin{bmatrix}\cos\theta_{z} & - \sin\theta_{z}&0\\sin\theta_{z}&\cos\theta_{z}&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&0&0 \\ 0 & \cos\theta_{x} & -\sin\theta_{x} \\ 0 & \sin\theta_{x} & \cos\theta_{x} \end{bmatrix}\begin{bmatrix}\ cos\theta_{y}&0&\sin\theta_{y}\\0&1&0\\-\sin\theta_{y}&0&\cos\theta_{y}\end{bmatrix}=\ begin{bmatrix} \cos{\theta_y}\cos{\theta_z}-\sin{\theta_x}\sin{\theta_y}\sin{\theta_z} & -\cos{\theta_x}\sin{\theta_z} & \cos{\theta_z}\sin{\theta_y}+\cos{\theta_y}\sin{\theta_x}\sin{\theta_z}\\ \cos{\theta_y}\sin{\theta_z}+\cos{\ theta_z}\sin{\theta_x}\sin{\theta_y}& \cos{\theta_x}\cos{\theta_z}&\sin{\theta_z}\sin{\theta_y}-\cos{\theta_z}\cos{\theta_y}\sin{\theta_x}\\ -\cos{\theta_x}\sin{\theta_y}& \sin{ \theta_x}& \cos{\theta_x}\cos{\theta_y}\end{bmatrix}$

$\theta_x = \arcsin(m_{32})$

= np.arcsin(2q2*q3 + 2q0*q1)

$\theta_{y}=\tan^{-1}\left(\begin{array}{c}{\frac{-m_{31}}{m_{33}}}\\\end{array}\right)$

=np.arctan2(

2q0q2 - 2q1q3
--------------------
1 - 2q1q1 - 2q2q2

)

$\theta_{z}=\tan^{-1}\left(\frac{-m_{12}}{m_{22}}\right)$

= np.arctan2(

2*q0*q3 - 2*q1*q2
---------------------------
1 - 2*q1*q1 - 2*q3* q3

)

The quaternion q corresponding to the Euler angles z, y, and x of the ZYX order is:

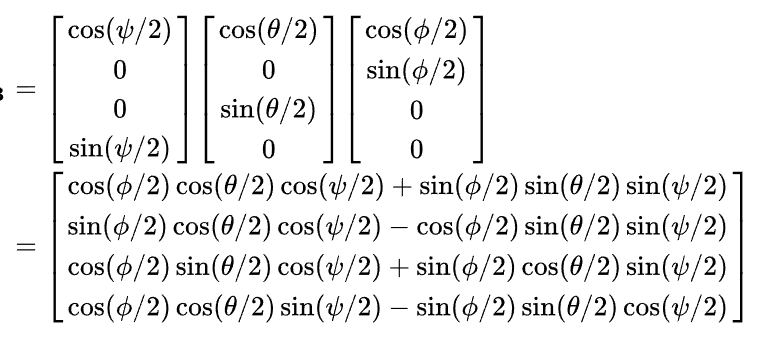
The Euler angles z, y, x in ZYX order means first rotate the z angle around the z axis of the fixed coordinate system, then rotate the y angle around the rotated y axis, and finally rotate the x angle around the rotated x axis. The z, y, and x here are all angles relative to the fixed coordinate system, not the angle relative to the rotated coordinate system. That is to say, z is the yaw angle (yaw) in the initial state, y is the pitch angle (pitch) in the initial state, and x is the roll angle (roll) in the initial state.