say up front
Today's blog is the blogger's most thoughtful blog this year. We haven't updated the data structure series for a long time. A few months ago, the blogger studied this binary balanced search tree in depth, and the blogger was deeply attracted by its search efficiency.
The AVL tree comes from a paper "An_algorithm_for_the_organization_of_information" in 1962 , which solves the problem of the degradation of ordinary binary search trees. This blogger will explain in detail later. Putting the AVL tree at present, its search efficiency is comparable to few data structures.
For this blog, the blogger has made a lot of preparations and tried a lot of drawing software, just to let everyone understand! I hope everyone will not be stingy with one button and three consecutive! !
foreword
那么这里博主先安利一下一些干货满满的专栏啦!
手撕数据结构![]() https://blog.csdn.net/yu_cblog/category_11490888.html?spm=1001.2014.3001.5482
https://blog.csdn.net/yu_cblog/category_11490888.html?spm=1001.2014.3001.5482算法专栏![]() https://blog.csdn.net/yu_cblog/category_11464817.html
https://blog.csdn.net/yu_cblog/category_11464817.html
STL源码剖析![]() https://blog.csdn.net/yu_cblog/category_11983210.html?spm=1001.2014.3001.5482
https://blog.csdn.net/yu_cblog/category_11983210.html?spm=1001.2014.3001.5482
What is an AVL tree?
Tips: The blogger will put a copy of the overall code at the end for your reference!
First, it is a binary search tree.
What is a binary search tree:
A binary search tree, also known as a binary sorting tree, is either an empty tree or a binary tree with the following properties:
- If its left subtree is not empty, the values of all nodes on the left subtree are less than the value of the root node
- If its right subtree is not empty, the values of all nodes on the right subtree are greater than the value of the root node
- Its left and right subtrees are also binary search trees
As shown in the figure: This is a binary search tree.
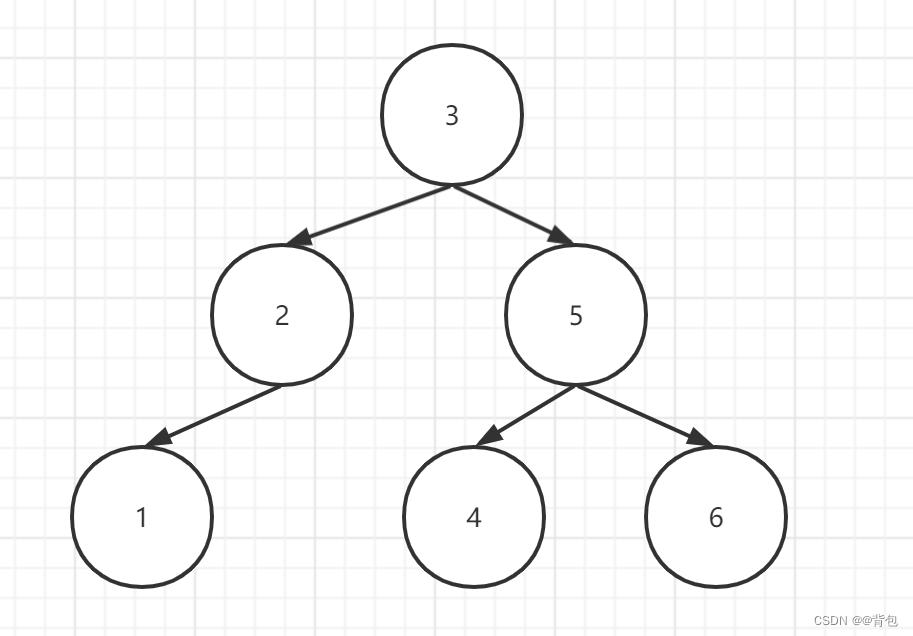
When we need to find node 4 in this search tree, we start from 3, bigger than 3, go right, smaller than 5, go left. In this way, we found the node 4.
The highest search complexity of a binary search tree is O(h), h is the height of the tree , so we can actually get better search efficiency. However, the search tree may degenerate. as the picture shows:
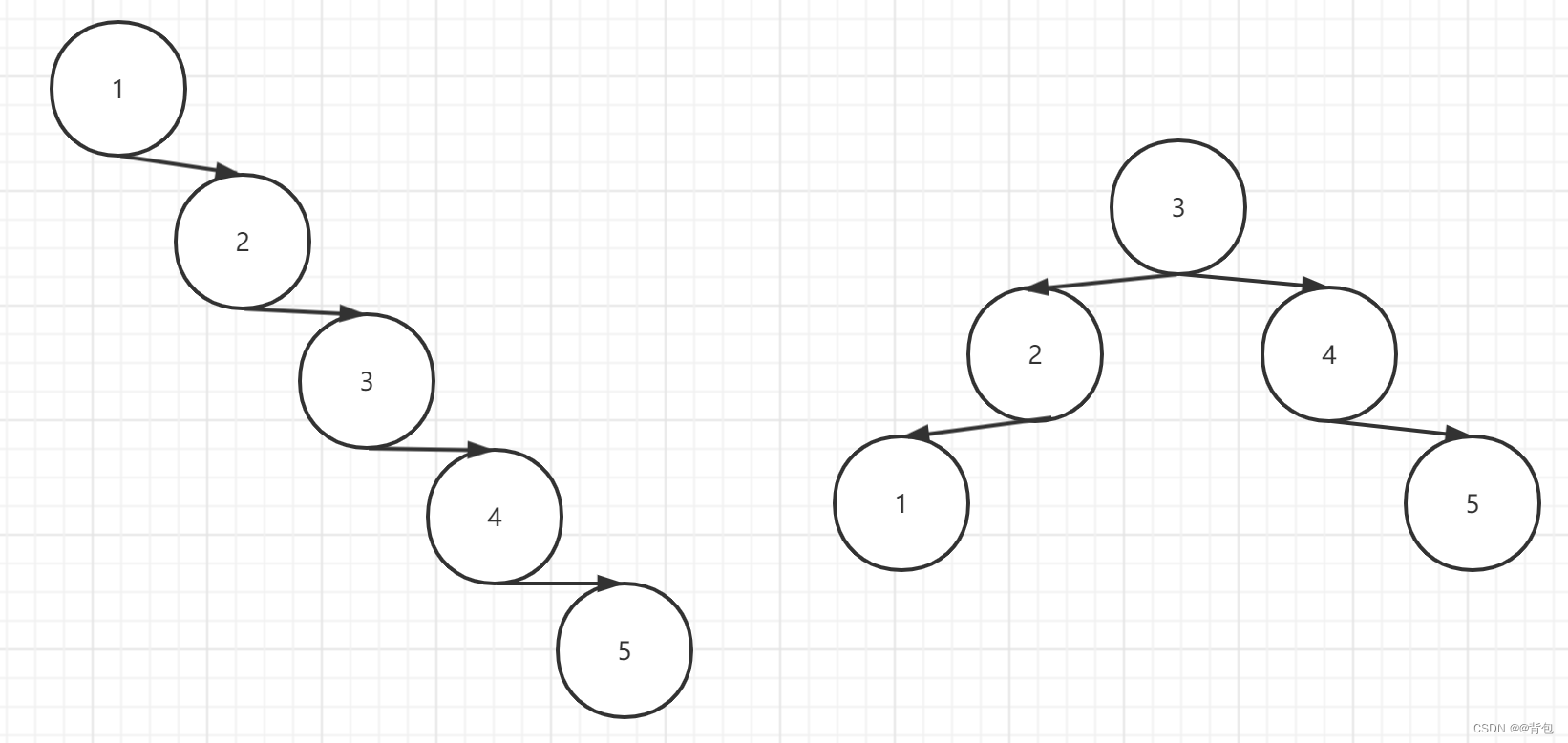
For example, in the first tree, if we want to find the bottom node, we need to find n times . For example, in the second tree, we need to search n/2 times to find the bottom node . Suppose we want to search 1 billion data, we need to search 500 million times, which is actually still O(n) level. In this case, lookups have no advantage. The main reason for this situation is that the height is unbalanced! We imagine a full binary tree, which is balanced, we look for a value, that is, the degree of height, and the complexity is O(logn). Therefore, we need to constantly transform the tree while inserting to balance its height, so that our search performance can be qualitatively improved! A binary balanced search tree searches for a value in 1 billion data, and searches up to 31 times. This kind of optimization is very large!
Therefore, we lead to a binary balanced search tree. Common binary balanced search trees include AVL trees and red-black trees.
An AVL tree is either an empty tree or a binary search tree with the following properties:
- Its left and right subtrees are both AVL trees
- The absolute value of the difference between the heights of the left and right subtrees (referred to as the balance factor) does not exceed 1 (-1/0/1)
- Balance Factor = Right Subtree Height - Left Subtree Height

Structure definition of AVL tree
AVL trees are usually constructed using triple chains. When we deal with pointers, we must remember that _parent must also be dealt with.
template<class K,class V>
struct AVLNode {
public:
AVLNode<K, V>* _left;
AVLNode<K, V>* _right;
AVLNode<K, V>* _parent;
pair<K, V>_kv;
int _bf; //balance factor
public:
AVLNode(const pair<K, V>& kv)
:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0) {}
};
template<class K, class V>
struct AVL {
typedef AVLNode<K, V>Node;
private:
Node* _root = nullptr;
public:
//成员函数
//...
}Insertion of AVL tree nodes (emphasis)
The node insertion of AVL tree can be divided into three steps:
- Insertion of new nodes
- Update of Balance Factor
- Determine whether the balance is broken by the balance factor, if the balance is broken, rotate
Rotation of AVL tree:
- left monorotation
- Right monorotation
- Left and right double rotation
- right-left birotation
The rotation of the AVL tree is the most important part of this blog, and the blogger will explain this part in detail!
1. Insertion of new nodes
The insertion steps of a new node are the same as those of a normal binary search tree. Find the insertion position and insert it directly!
bool insert(const pair<K, V>& kv) {
if (_root == nullptr) {
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_kv.first < kv.first) {
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) {
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(kv);
if (parent->_kv.first < kv.first) {
parent->_right = cur;
}
else {
parent->_left = cur;
}
cur->_parent = parent;
//先更新平衡因子
//...
//平衡因子更新后,判断是否需要旋转
return true;
}2. Update the balance factor
When a new node is inserted, the nodes on the node's ancestor path may be affected , and we need to update it according to the situation. As shown in the figure: After inserting a node, only the balance factor of the node on the ancestor path will be affected.
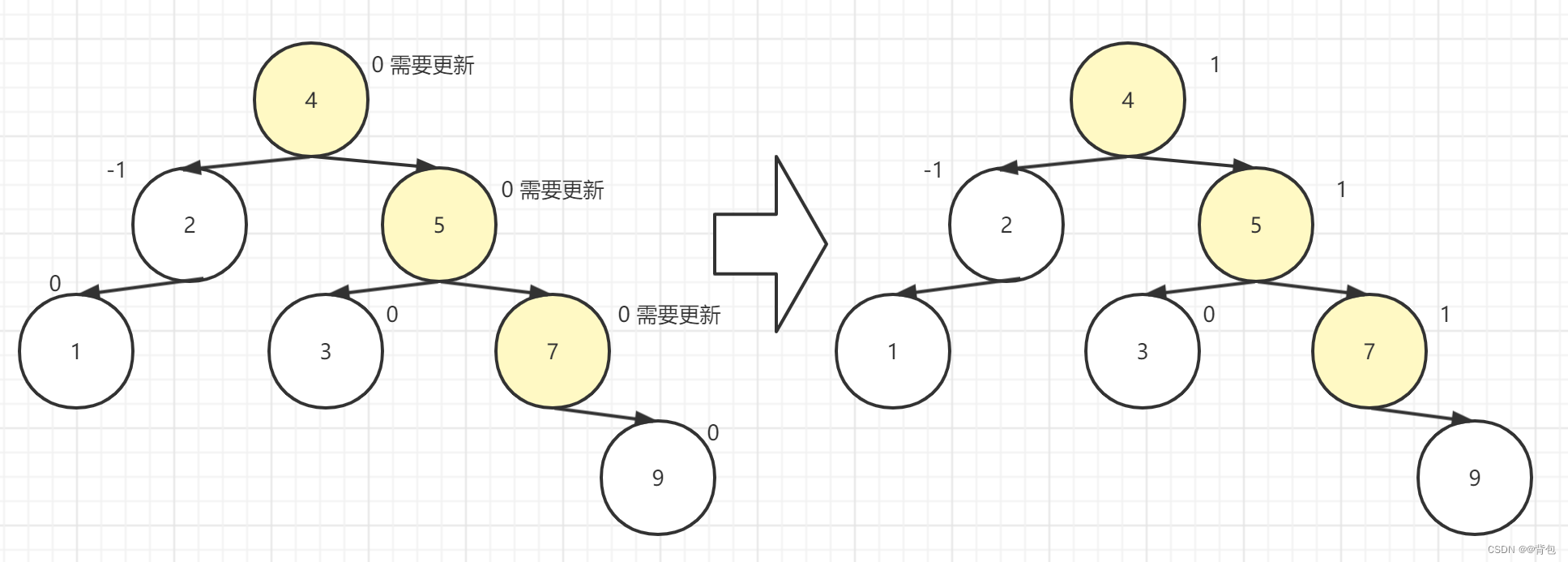
We only need to use the _parent pointer to iterate upwards.
- If inserted to the right of the "new node's father", the father's balance factor ++
- If inserted to the left of the "new node father", the father's balance factor - -
Tips: The blogger will put a copy of the overall code at the end for your reference!
If the balance factor is 1/-1 after updating, it means that the height of the subtree has been changed, and it is necessary to continue to iterate upwards. If the balance factor is 0 after the update, it means that the new node just fills up the incomplete subtrees (this is easy to understand, if you don’t understand, you can simply draw a picture), if the balance factor is 2/-2 after the update, Indicates that the balance is broken and needs to be rotated
while (parent) {//只有根没有父亲
//最坏可能需要更新到根
if (cur == parent->_right) {
parent->_bf++;
}
else {
parent->_bf--;
}
if (parent->_bf == 0) {
//高度不变 -- 停止更新
break;
}
else if (parent->_bf == 1 || parent->_bf == -1) {
//继续更新
parent = parent->_parent;
cur = cur->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2) {
//说明parent所在的子树已经不平衡了 -- 需要旋转
}
else {
assert(false);//理论上不能走到这里
}
}3. Rotation
Rotation of AVL tree:
- left monorotation
- Right monorotation
- Left and right double rotation
- right-left birotation
First, let's look at a few examples to get a general idea of what kind of operation rotation is, and see how the rotation method balances an unbalanced tree:
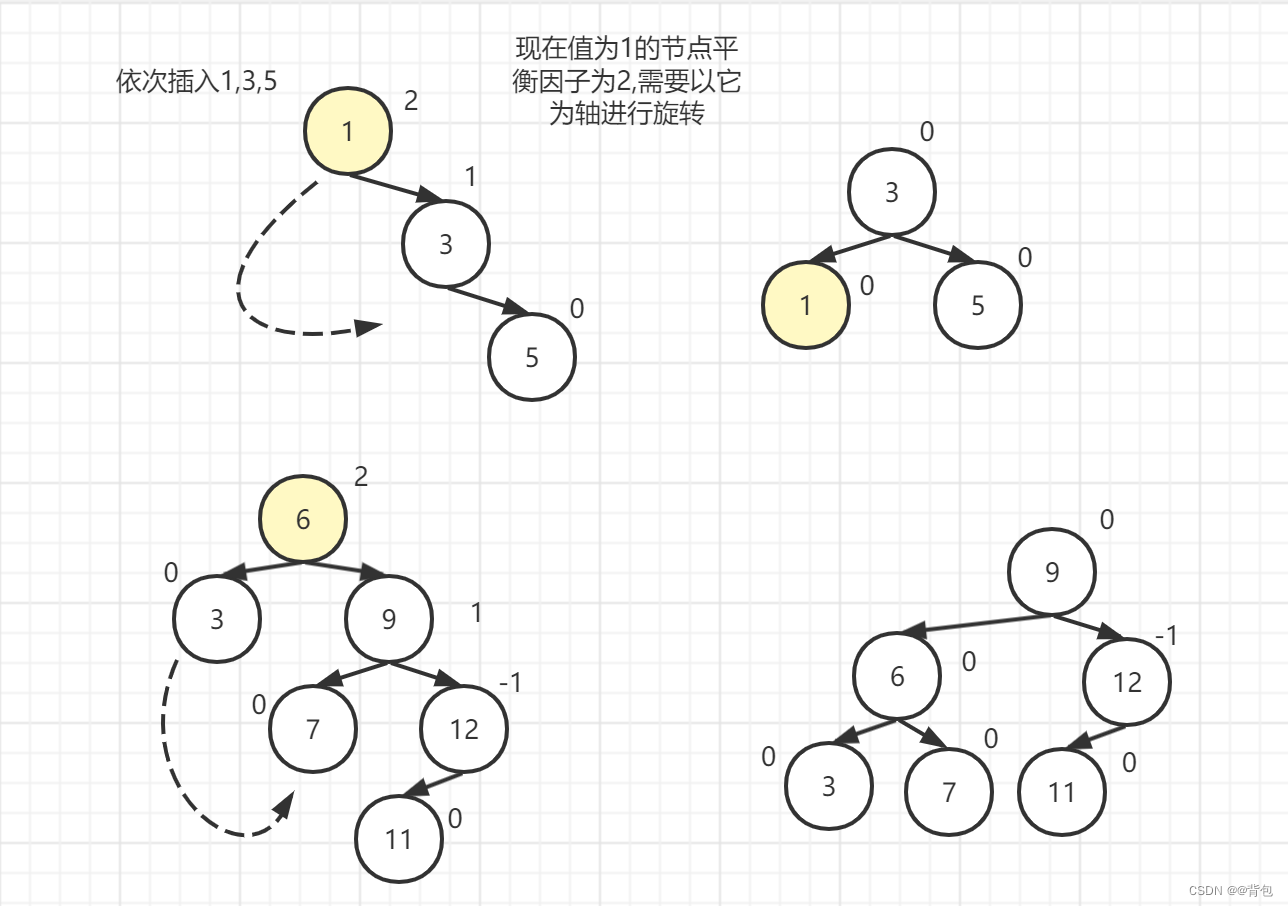
Here only one of the situations in the rotation is shown, the left single rotation, and now the blogger will explain it in detail in four situations
Left single rotation: the new node is inserted to the right of the higher right subtree
Please note that the trigger condition here is that the higher one is the right subtree, and the insertion is on the right side of the right subtree
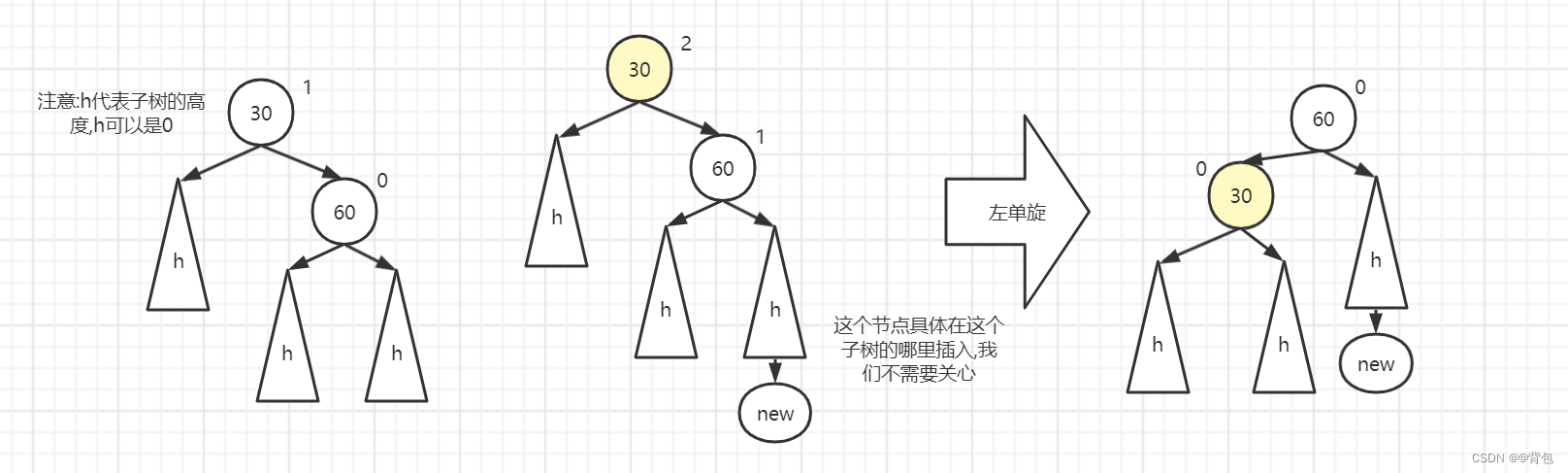
In fact, just take down 30 and replace it with 60
At this point we should pay attention, here we find the point where the balance factor is abnormal, that is, the node 30, it is not necessarily the root of the whole tree, it may just be the root of a subtree , but during the rotation process, we do not need Concerned about the structure on it, after we complete the rotation, just re-link it.
Label the important nodes with names and how to rotate them, we can see at a glance, because it is a trident chain, we can directly operate the pointer!
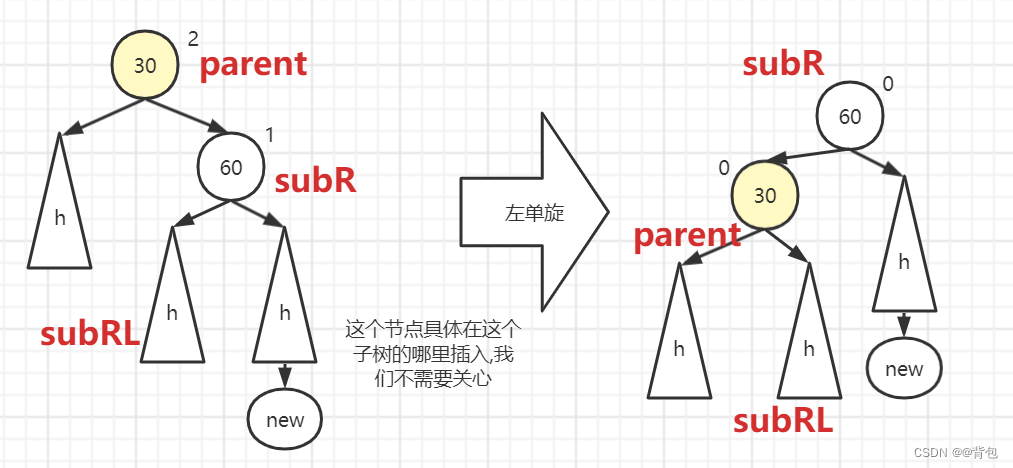
We convert ideas into code:
First of all, right and right trigger left single rotation, that is, parent->_bf==2&&cur->_bf==1 (cur is the right child of parent in the above figure) , this time triggers left single rotation.
if (parent->_bf == 2 && cur->_bf == 1) {
//注意这里肯定是bf==1的情况 -- 才是单旋
//parent->_bf==2说明是左单旋
rotate_left(parent);//旋转就动了6个指针 -- O(1)
} void rotate_left(Node* parent) {
//当然我们还要注意处理parent指针
//parent和subR不可能为空 -- ,但是subRL可能为空
//1.parent是整颗树根
//2.parent是子树的根
//最后更新一下平衡因子
//只有subR和parent的平衡因子受到了影响
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL) {
subRL->_parent = parent;
}
Node* ppNode = parent->_parent;//记录一下原先parent的parent
subR->_left = parent;
parent->_parent = subR;
if (_root == parent) {
_root = subR;
subR->_parent = nullptr;
}
else {
//如果ppNode==nullpt,是不会进来这里的
if (ppNode->_left == parent) {
ppNode->_left = subR;
}
else {
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
//更新一下平衡因子
subR->_bf = parent->_bf = 0;//这个看图就行了
}Right single rotation: the new node is inserted to the left of the higher left subtree
Please note that the trigger condition here is that the higher one is the left subtree, and the insertion is on the left side of the left subtree
This is actually a mirror image of the left single rotation. The blogger gave you the picture. I believe we can write the code by ourselves.
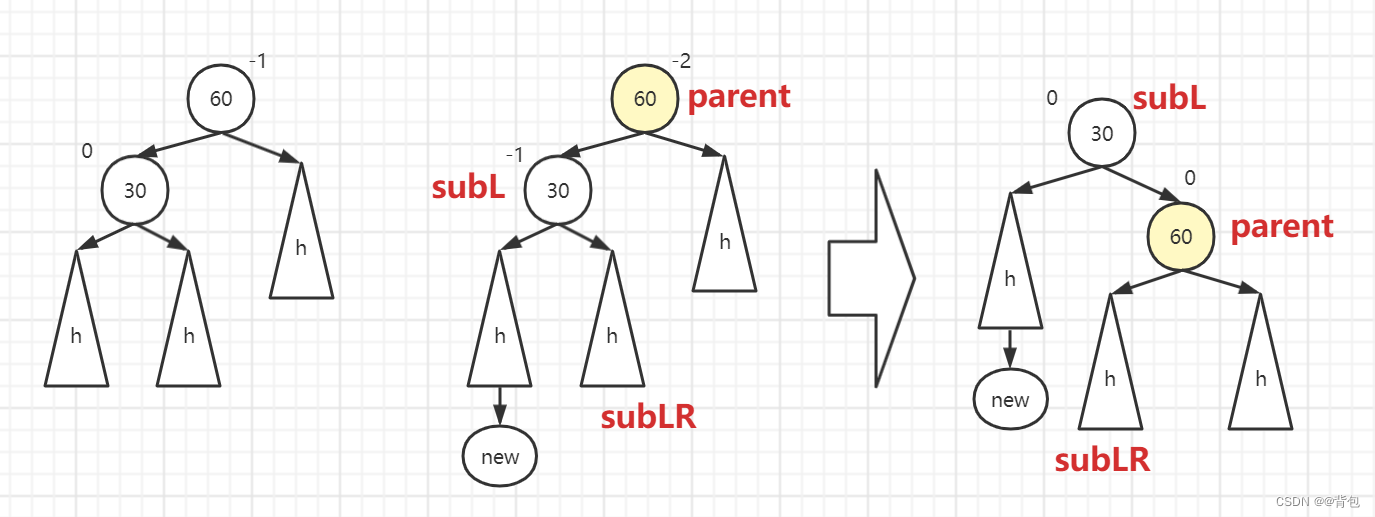
From the picture, we can know that when the trigger condition is parent->_bf==-2&&cur->_bf==-1
code show as below:
else if (parent->_bf == -2 && cur->_bf == -1) {
//右单旋
rotate_right(parent);
}//右单旋 -- 思路和左单旋是镜像 -- 很简单
void rotate_right(Node* parent) {
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR) {
subLR->_parent = parent;
}
Node* ppNode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (_root == parent) {
_root = subL;
subL->_parent = nullptr;
}
else {
if (ppNode->_left == parent) {
ppNode->_left = subL;
}
else {
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
//更新平衡因子
subL->_bf = parent->_bf = 0;
}Double spin:
Seeing this, can these two single rotations solve all problems? The answer is no, let's give an example:
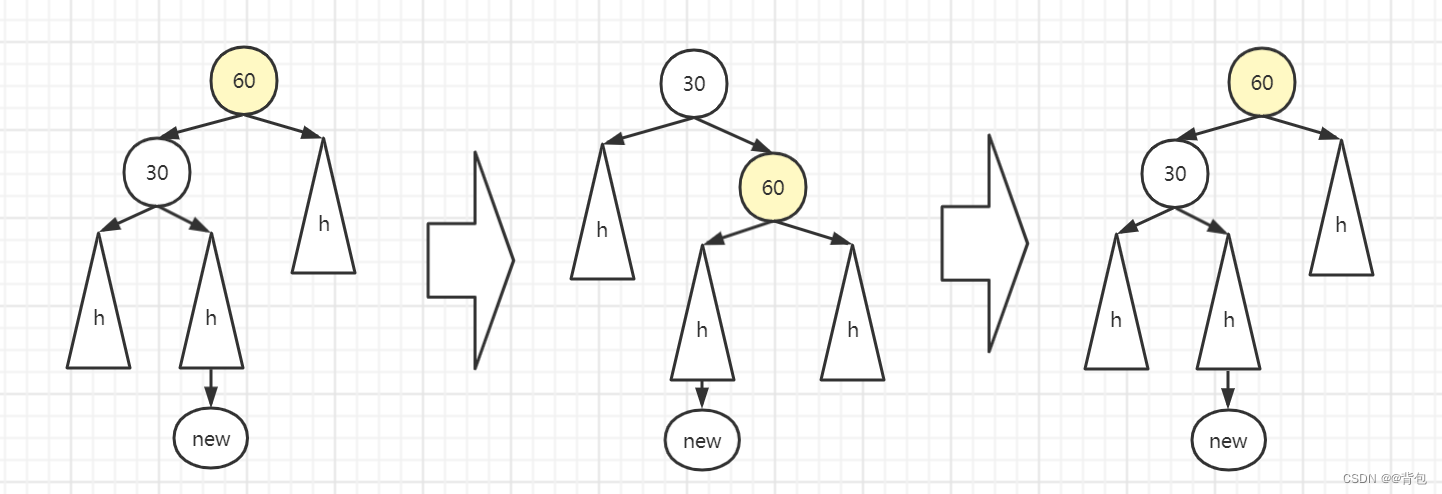
We can see this situation, no matter how single-spin, we can't make the tree balance.
From this we derive the double spin:
Left and right double rotation: new nodes are inserted into the right side of the higher left subtree: first left rotation and then right rotation
The process of double rotation is more complicated than that of single rotation
Among them, there are three insertion situations for left and right double rotation, as shown in the figure:

Case 3: h==0, at this time 60 is the newly inserted node
Here's how the rotation works:
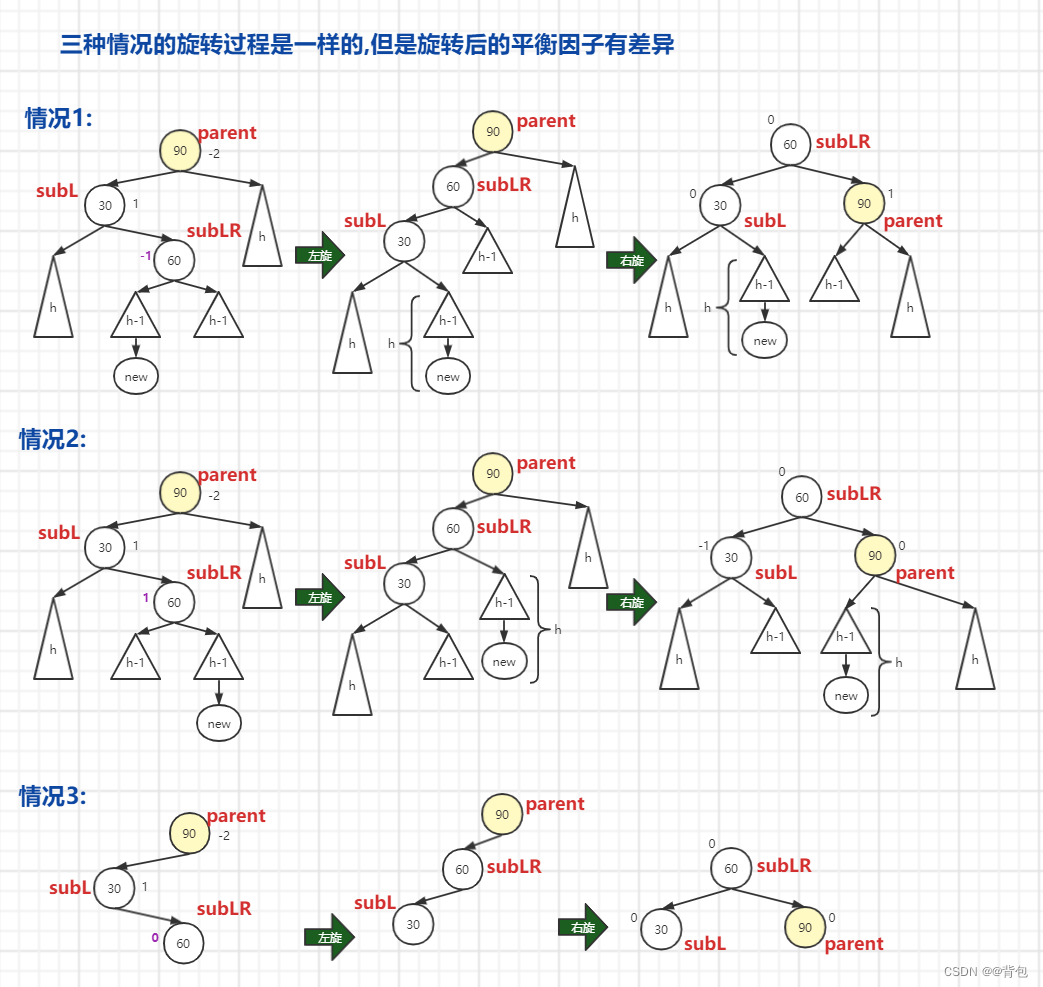
I believe that the above figure has explained the rotation process very clearly. In fact, it is a combination of two single rotations.
Now we want to focus on updating the balance factor after rotation:
We can find that the final balance factor depends on the balance factor of subLR in the initial state
Case 1: subLR->_bf==-1
- After rotation, the balance factors of parent, subL, and subLR are 1, 0, and 0 respectively
Case 2: subLR->_bf==1
- After rotation, the balance factors of parent, subL, and subLR are 0, -1, and 0 respectively
Case 3: subLR->_bf==0
- After rotation, the balance factors of parent, subL, and subLR are 0, 0, and 0 respectively
Now we only need to compare the pictures and the adjusted balance factor to quickly write the code:
First of all, we can know from the pictures that the triggering conditions for left and right double rotation are:
parent->_bf == -2 && cur->_bf == 1
else if (parent->_bf == -2 && cur->_bf == 1) {
//左右双旋
rotate_left_right(parent);
} void rotate_left_right(Node* parent) {
//要在单旋之前记录一下,因为单旋之后平衡因子会变
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;//记录一下subLR的平衡因子
rotate_left(parent->_left);//先最左边进行一个左旋
rotate_right(parent);//再对自己进行一个右旋转
//如何区分三种情况的平衡因子更新呢?
subLR->_bf = 0;//一定要画图!三种情况的subLR最终都是0
if (bf == 1) {
//情况1
parent->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1) {
//情况2
parent->_bf = 1;
subL->_bf = 0;
}
else if (bf == 0) {
//情况3
parent->_bf = 0;
subL->_bf = 0;
}
else assert(false);
}Right-left double-rotation: new nodes are inserted to the left of the higher right subtree: first right-handed and then left-handed
Similarly, there are three cases of right-left double rotation.
Right-left double-rotation is actually a mirror image of left-right double-rotation. If you understand left-right double-rotation, right-left double-rotation can be drawn directly, and the balance factors of the three situations can be summarized. Just write the code directly.
Triggering conditions:
parent->_bf == 2 && cur->_bf == -1
else if (parent->_bf == 2 && cur->_bf == -1) {
//右左双旋
rotate_right_left(parent);
} void rotate_right_left(Node* parent) {
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
rotate_right(parent->_right);
rotate_left(parent);
subRL->_bf = 0;
if (bf == 1) {
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1) {
subR->_bf = 1;
parent->_bf = 0;
}
else if (bf == 0) {
subR->_bf = 0;
parent->_bf = 0;
}
else assert(false);
}Fourth, the inspection of AVL tree
After writing here, we can try to insert some nodes and check whether the AVL tree is balanced
Of course, we can check this tree by debugging and breaking points, but this is very troublesome.
At the same time, we cannot judge the validity of the AVL tree by checking whether the in-order traversal is in order. Because all search tree in-order traversals are in order.
We need to check through the properties of the AVL tree to check whether the height difference between the left and right subtrees of each subtree is less than or equal to 1:
Of course, it is actually very simple for us to write this kind of code now. Here is also a portal for deducting questions. In fact, it is the inspection of the AVL tree. You can complete it by the way.
Interview question 04.04. Check balance ![]() https://leetcode.cn/problems/check-balance-lcci/ Here bloggers also provide code for inorder traversal:
https://leetcode.cn/problems/check-balance-lcci/ Here bloggers also provide code for inorder traversal:
class AVL {
//...
//...
//...
public:
void inorder() {
_inorder(this->_root);
}
bool is_balance() {
return _is_balance(this->_root);
}
private:
void _inorder(Node* root) {
if (root == nullptr) {
return;
}
_inorder(root->_left);
cout << (root->_kv).first << ":" << (root->_kv).second << endl;
_inorder(root->_right);
}
int _height(Node* root) {
if (root == nullptr)return 0;
int leftHT = _height(root->_left);
int rightHT = _height(root->_right);
return max(leftHT, rightHT) + 1;
}
bool _is_balance(Node* root) {
if (root == nullptr)return true;
int leftHT = _height(root->_left);//左子树高度
int rightHT = _height(root->_right);//右子树高度
int diff = rightHT - leftHT;
//把平衡因子也检查一下
if (diff != root->_bf) {
cout << root->_kv.first << "的平衡因子异常" << endl;
return false;
}
return abs(diff) < 2
&& _is_balance(root->_left)//判断一下左子树是否平衡
&& _is_balance(root->_right);//判断一下右子树是否平衡
}
}Five, delete and other interfaces
At this point, some partners may ask, why talk about AVL and not delete those interfaces?
Because, school recruitment, company interviews, and future work will basically not examine the deletion interface of the AVL tree, and the red-black tree is the same, we only need to master the insertion interface.
AVL tree, red-black tree, we are all doing comprehension learning, we don’t need to tear all its codes by hand, so the time cost is very high, and the meaning is not great. When we learn AVL tree, we need to understand its structure in depth , learn a plug-in interface, we can already do this very well.
Here the blogger roughly talks about the steps to delete:
At the beginning, it is like searching a tree to find the node to be deleted, and delete it with the replacement method. After deletion, the same is true, and the balance is checked. If the balance is broken, rotate it. This process is actually the opposite of insertion.
Six, AVL.h overall code
#pragma once
#include<map>
#include<set>
#include<algorithm>
#include<assert.h>
#include<time.h>
using namespace std;
template<class K,class V>
struct AVLNode {
public:
AVLNode<K, V>* _left;
AVLNode<K, V>* _right;
AVLNode<K, V>* _parent;
pair<K, V>_kv;
int _bf; //balance factor
public:
AVLNode(const pair<K, V>& kv)
:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0) {}
};
//如何更新平衡因子
//如何旋转
template<class K, class V>
struct AVL {
typedef AVLNode<K, V>Node;
private:
Node* _root = nullptr;
private:
//左单旋
void rotate_left(Node* parent) {
//当然我们还要注意处理parent指针
//parent和subR不可能为空 -- ,但是subRL可能为空
//1.parent是整颗树根
//2.parent是子树的根
//最后更新一下平衡因子
//只有subR和parent的平衡因子受到了影响
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL) {
subRL->_parent = parent;
}
Node* ppNode = parent->_parent;//记录一下原先parent的parent
subR->_left = parent;
parent->_parent = subR;
if (_root == parent) {
_root = subR;
subR->_parent = nullptr;
}
else {
//如果ppNode==nullpt,是不会进来这里的
if (ppNode->_left == parent) {
ppNode->_left = subR;
}
else {
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
//更新一下平衡因子
subR->_bf = parent->_bf = 0;//这个看图就行了
}
//右单旋
void rotate_right(Node* parent) {
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR) {
subLR->_parent = parent;
}
Node* ppNode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (_root == parent) {
_root = subL;
subL->_parent = nullptr;
}
else {
if (ppNode->_left == parent) {
ppNode->_left = subL;
}
else {
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
//更新平衡因子
subL->_bf = parent->_bf = 0;
}
//左右双旋
void rotate_left_right(Node* parent) {
//要在单旋之前记录一下,因为单旋之后平衡因子会变
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;//记录一下subLR的平衡因子
rotate_left(parent->_left);//先最左边进行一个左旋
rotate_right(parent);//再对自己进行一个右旋转
//如何区分三种情况的平衡因子更新呢?
subLR->_bf = 0;//一定要画图!三种情况的subLR最终都是0
if (bf == 1) {
//情况1
parent->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1) {
//情况2
parent->_bf = 1;
subL->_bf = 0;
}
else if (bf == 0) {
//情况3
parent->_bf = 0;
subL->_bf = 0;
}
else assert(false);
}
//右左双旋
void rotate_right_left(Node* parent) {
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
rotate_right(parent->_right);
rotate_left(parent);
subRL->_bf = 0;
if (bf == 1) {
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1) {
subR->_bf = 1;
parent->_bf = 0;
}
else if (bf == 0) {
subR->_bf = 0;
parent->_bf = 0;
}
else assert(false);
}
public:
//我们先不返回pair,到时候我们封装map的时候在搞
bool insert(const pair<K, V>& kv) {
if (_root == nullptr) {
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_kv.first < kv.first) {
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) {
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(kv);
if (parent->_kv.first < kv.first) {
parent->_right = cur;
}
else {
parent->_left = cur;
}
cur->_parent = parent;
//控制平衡
//先更新平衡因子
while (parent) {//只有根没有父亲
//最坏可能需要更新到根
if (cur == parent->_right) {
parent->_bf++;
}
else {
parent->_bf--;
}
if (parent->_bf == 0) {
//高度不变 -- 停止更新
break;
}
else if (parent->_bf == 1 || parent->_bf == -1) {
//继续更新
parent = parent->_parent;
cur = cur->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2) {
//说明parent所在的子树已经不平衡了 -- 需要旋转
//左旋
if (parent->_bf == 2 && cur->_bf == 1) {
//注意这里肯定是bf==1的情况 -- 才是单旋
//parent->_bf==2说明是左单旋
rotate_left(parent);//旋转就动了6个指针 -- O(1)
}
else if (parent->_bf == -2 && cur->_bf == -1) {
rotate_right(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1) {
//左右双旋
rotate_left_right(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1) {
//右左双旋
rotate_right_left(parent);
}
else assert(false);
break;
}
else {
assert(false);//理论上不能走到这里
}
}
return true;
}
public:
void inorder() {
_inorder(this->_root);
}
bool is_balance() {
return _is_balance(this->_root);
}
private:
void _inorder(Node* root) {
if (root == nullptr) {
return;
}
_inorder(root->_left);
cout << (root->_kv).first << ":" << (root->_kv).second << endl;
_inorder(root->_right);
}
int _height(Node* root) {
if (root == nullptr)return 0;
int leftHT = _height(root->_left);
int rightHT = _height(root->_right);
return max(leftHT, rightHT) + 1;
}
bool _is_balance(Node* root) {
if (root == nullptr)return true;
int leftHT = _height(root->_left);//左子树高度
int rightHT = _height(root->_right);//右子树高度
int diff = rightHT - leftHT;
//把平衡因子也检查一下
if (diff != root->_bf) {
cout << root->_kv.first << "的平衡因子异常" << endl;
return false;
}
return abs(diff) < 2
&& _is_balance(root->_left)//判断一下左子树是否平衡
&& _is_balance(root->_right);//判断一下右子树是否平衡
}
};
void test1() {
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
AVL<int, int>t1;
for (auto e : a) {
t1.insert(make_pair(e, e));
}
t1.inorder();
cout << "is_balance():" << t1.is_balance() << endl;
}
void test2(){
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
AVL<int, int>t1;
for (auto e : a) {
t1.insert(make_pair(e, e));
}
t1.inorder();
cout << "is_balance():" << t1.is_balance() << endl;
}
void test3(){
size_t N = 10000;
srand(time(nullptr));
AVL<int, int>t1;
for (size_t i = 0; i < N; ++i) {
int x = rand();
t1.insert(make_pair(x, i));
}
cout << "is_balance():" << t1.is_balance() << endl;
}7. Summary
Seeing this, everyone should have a deeper understanding of the implementation of the AVL tree, the focus is on its rotation. The blogger of this blog has spent a lot of thought on drawing pictures, and also invested a lot of time in drawing pictures. The next issue will bring you the content of the red-black tree. I hope everyone can support a lot, one-click three links, like, follow, collect and comment, and then leave!
(Please indicate the author and source when reprinting. Do not use for commercial purposes without permission.)
For more articles, please visit my homepage
