BGW protocol (arithmetic sharing)

overview

The BGW protocol can be used to evaluate arithmetic circuits including addition, multiplication, and constant multiplication gates on the domain. This protocol can rely on the Shamir secret sharing scheme and use its homomorphic characteristics to properly process each secret share. perform secure calculations.

Addition gate

Arithmetic addition sharing (two parties)

One party holds the ciphertext and the other holds the key.

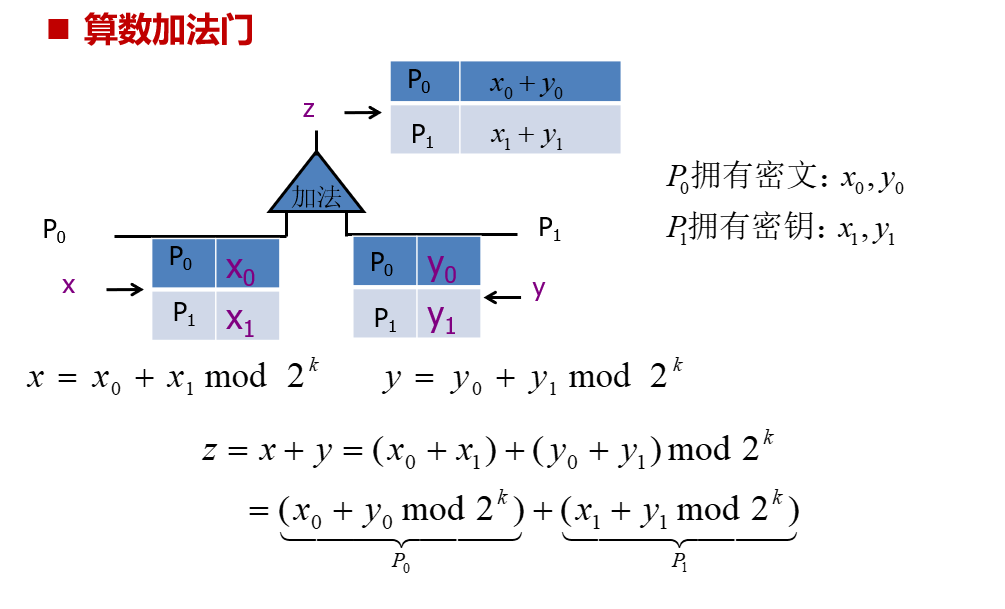
Obviously, the arithmetic addition gate completes the calculation result without interaction, and the calculation can be completed locally. (The GMW protocol is equivalent to mod 2 computing.)

Additive sharing based on Shamir scheme (multi-party)

Consider two input gates $x,y$ , an output gate$The\; addition\; gate\; of\; z$ , calculate$z=y+x$ . Also, to achieve sharing, the input wire values ​​of the two input gates need to be secretly split among multiple parties. First for each input wire for the value to be entered$xory$ , select a$A\; polynomial\; of\; order\; t$ , then Shamir's$(t,n)$ share, distribute the secret share to other participants, so assuming that there are$n$ participants, then you will get$n$ secret shares from different input wires. Local summation and accumulation, the output gatezzOne of the$z-$$(t,n)$ share. Just$t+One$ or more joint reconstruction secrets can restore the final addition result.

multiplication gate

Arithmetic multiplication shared (two parties)

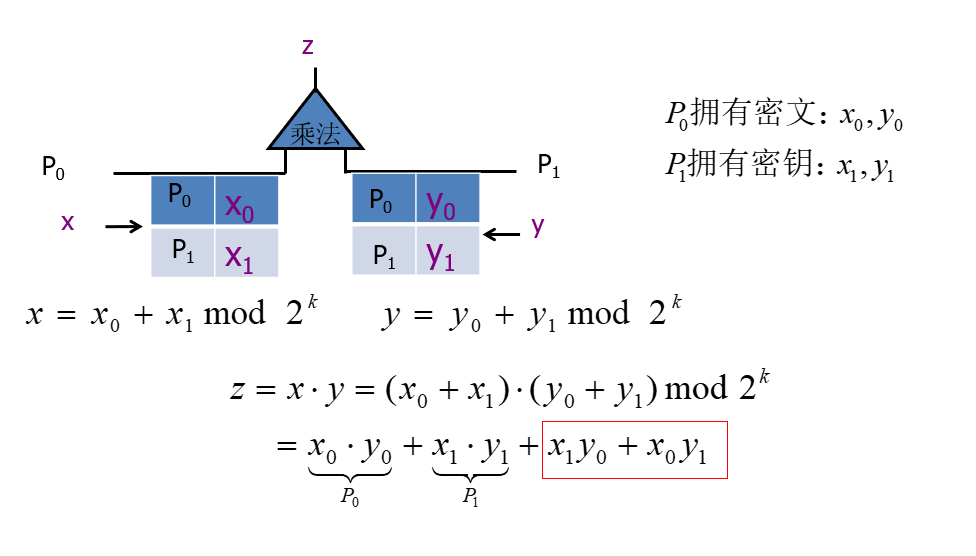
Obviously, like the GMW protocol, in addition to the part that can be calculated by itself, there will be more results that must be calculated through interaction. If the same OT protocol as Boolean sharing is used, there are many possible situations for each unknown data, and there are even more combinations of multiples. In order to protect privacy and cover the output of the sub-circuit, it is necessary to add a mask. Here, a multiplication triplet is used.

Beaver triples (multiplicative triples)

A construction paradigm of the MPC protocol : it is divided into a preprocessing stage when the input of the participant is unknown and an online stage when the input is selected by the participant . The preprocessing stage will generate some random quantities that have a certain correlation with each other for the participants. Participants can consume these random amounts during the online phase.
In the previous approach, we can see that the only real overhead in the protocol is the communication overhead in evaluating each multiplication gate, hence the adoption of triplets here shifts most of the communication to the preprocessing stage.
The so-called multiplication triplet, namely $ab=c$,$a$ and$b$ is a random number randomly selected from the field, and each multiplication gate evaluation needs to consume a triplet

Step
Still consider two input gates $x,y$ , an output gate$The\; multiplication\; gate\; of\; z$ , computing$x\ast y=z$ , first add a mask to the two input values, that is, split the elements of the triplet in two ways. That is$a=a_0+a_1,b=b_0+b_1$, Let the two parties hold a part respectively, notice that $ab=(a_0+a_1)(b_0+b_1)=a_0{b}_0+a_0{b}_1+a_1{b}_0+a_1{b}_1$, split it into two parts $(ab{)}_0$sum $(ab{)}_1$
The specific operation can call the method of homomorphic encryption, assuming that a homomorphic encryption algorithm (such as Paillier) is selected

• $P_1$CalculateE $And(a_1),E(b_1)$ and send to$P_0$
• $P_0$计算$E\left(b_1{)}^{a_0}And\right(a_1{)}^{b_0}And(a_0{b}_0-a_1{b}_1)=And(a_0{b}_0+a_0{b}_1+a_1{b}_0-a_1{b}_1)$ to$P_1$
• $P_1$just decrypt
• At this time $(ab{)}_0=a_1{b}_1$，而$(ab{)}_1=a_0{b}_0+a_0{b}_1+a_1{b}_0$

Currently two parts have $x_i,y_i,a_i,b_i$。

• 让$x,y$ in a masked manner$e=x+a$和$f=y+b$ export, immediate release$x_i+a_i,y_i+b_i$, so that both parties can locally calculate $e,f$
• Calculate $\begin{array}{rl}xy& =(e-a)(f-b)\\ & =ef-fa-eb+ab\end{array}$, then split it up and get $\begin{array}{l}(xy{)}_0=-f{a}_0-e{b}_0+(ab{)}_0\\ (xy{)}_1=ef-f{a}_1-e{b}_1+(ab{)}_1\end{array}$
• Cooperate with the previously calculated $(ab{)}_0$sum $(ab{)}_1$The result can be obtained locally.

multiplicative sharing

Shamir-based secret distribution scheme

= Still consider two input gates $x,y$ , an output gate$The\; multiplication\; gate\; of\; z$ , computing$x\ast y=z$ , intuitively, is essentially$Multiply\; polynomials\; of\; degree\; t$ , this will give a degree$2$ polynomial in$t$$q\left(x\right)$ , the secret share of each participant is a point on this polynomial$q(i)=[v_x][v_y]$ (Note:$\left[\right]$ stands for$(t,n)$ Shamir’s secret share), obviously recovering the correct result requires at least$2t\_+1$ secret share, which already exceeds the threshold tt of the Shamir secret sharing$t$ , so how to solve the threshold overflow problem? There is no doubt that the product polynomials need to be reduced in order. Note: The requirement 2 t + 1 < n 2t+1<n
needs to be met here$2t\_+1<n$ , that is, the security is based on the majority-honest assumption.
Goal: get$effective\; secret\; shares\; for\; q\left(0\right)$ with polynomial order not exceeding threshold$t$ , so that$t+1$ person can recover the secret$q\left(0\right)$ .
The core idea: use the linear function of the secret share of the participants to express$q(0)={\sum }_{i=1}^{2t+}{l}_{i}q\left(i\right)$ , which is a$(t,n)$ share-to-addition$A\; form\; of\; t$ , that is,$q\left(0\right)$ is converted to$2t\_+$Sum of$1\; secret\; share.$Then the number of the participant is$[1,\mathrm{2..2}t]$ such a growth method, add$l_i$Is a value that can be calculated by knowing the number, then you can simulate $2t\_+1$ secret share for summing.

The specific step-down steps are as follows:

1. First, each participant based on its own $q\left(i\right)$ performs a Shamir's$(t,n)$ secret share, and the corresponding secret share$\left[q\right(i)]$ is sent to other participants, that is, each participant sends$q\left(i\right)$ as secret and constant term, choose a$The\; t$ -order polynomial distributes the corresponding sub-secret shares to other participants.
2. Each participant calculates locally $[q(0)]={\sum }_{i=1}^{2t+}{l}_i[q(i)]$，$\left[q\right(0)]$ represents the product secret value$The\; effective\; share\; of\; q\left(0\right)$ ,$l_i$is the corresponding Lagrange coefficient.

At this time because $\left[q\right(i)]$ is a$(t,n)$ sharing, then everyone calculates$\left[q\right(0)]$ is a$(t,n)$ sharing. This completes the step-down operation.

Based on random input and triplet scheme (additive secret sharing)

Each party constructs triplets $[a][b]=\left[c\right]$ (Hold by oneself, other participants do not know, knowing ab, c is determined), each participant holds a secret share$[v_x],\left[v_y\right]$ (For each participant's input wire, a secret share will be randomly assigned, only the corresponding participant knows its value, and$v={\sum }_{i=1}^n\left[v\right]$ ) want to calculate$[v_x{v}_y]$
(Note:$\left[\right]$ is the sub-secret share shared by addition, namely$a={\sum }_{i=1}^n[a],b={\sum }_{i=1}^n\left[b\right]$ ), the calculation steps are as follows

1. Each participant calculates locally $[d]=[v_x-a]$ and publicly
2. Each party computes locally $[e]=[v_y-b]$ and publicly
3. Then there is the following equation

$\begin{array}{rl}{v}_x{v}_y& =(v_x-a+a)(v_y-b+b)\\ & =(d+a)(e+b)\\ & =de+db+ae+ab\\ & =de+db+ae+c\end{array}$
$d,e$ is disclosed, and$[a],[b],\left[c\right]$ Each participant holds, so each participant can calculate the secret share
$[v_x{v}_y]=de+d[b]+and\left[to\right]+[c]$

reference

Introduction to Practical Secure Multi-Party Computation
Arithmetic Sharing