[Classic Question] Binary Search Tree and Doubly Linked List

Binary search tree and doubly linked list link

problem solving ideas

Idea 1: In-order traversal, put the nodes into the vector, and then change the link relationship. This is easy to come up with and solve, but it obviously does not meet the meaning of the question.

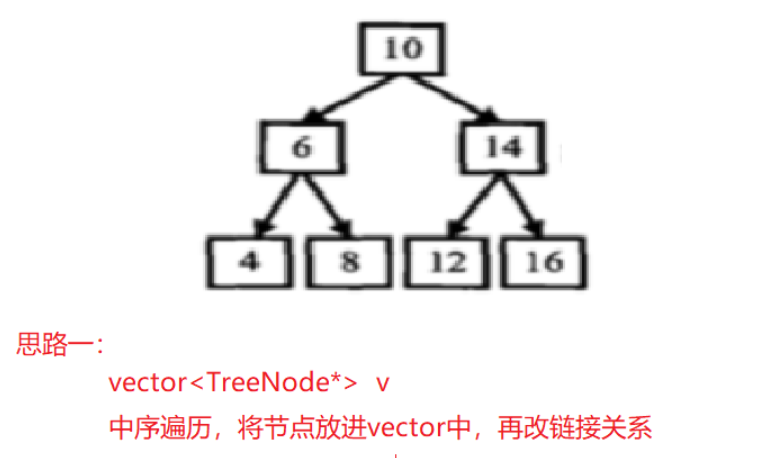
Idea 2:
This question requires converting a binary search tree into a sorted doubly linked list without creating new nodes and only adjusting pointers.
The characteristic of a binary search tree is that the values ​​of the left subtree are smaller than the root node, and the values ​​of the right subtree are greater than the root node, and an ascending sequence can be obtained by in-order traversal.
Therefore, we can use the order of in-order traversal to point the left pointer of each node to the previous node, and point the right pointer of each node to the next node, thus forming a doubly linked list.
We need to use a variable prev to record the previous node, initially nullptr. Then we recursively traverse the binary tree, and every time we visit a node, we modify the pointer to it and prev, and update prev to the current node.
Finally, we start from the root node and go left, find the leftmost node, which is the head node of the doubly linked list, and just return.

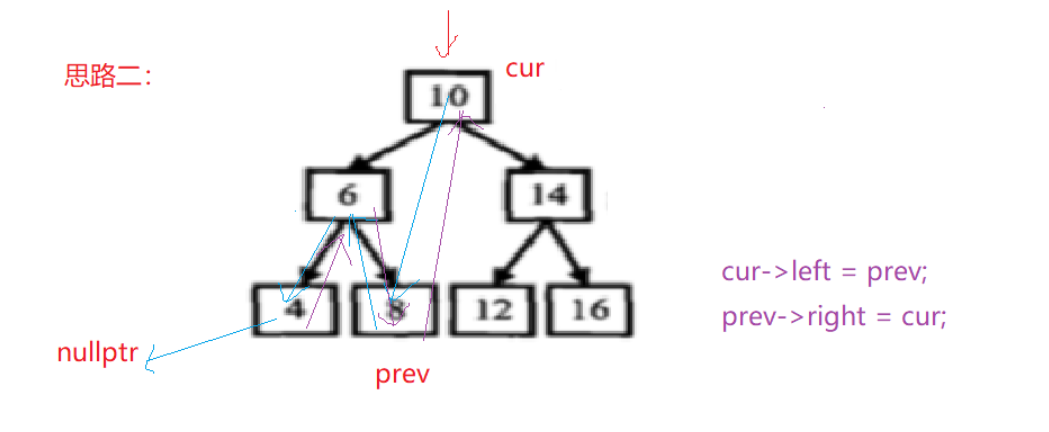
Take a chestnut:
Suppose we have such a binary search tree:

       10
      /  \
    6    14
    / \   / \
   4   8 12 16

We first initialize prev to be empty, and then recursively traverse the binary tree from the root node.

First, we traverse to the node 4, which has no left subtree, so we directly modify its left pointer to point to prev (empty at this time), and then update prev to 4.

Then we go back to the node 6, which has a left subtree, so we modify its left pointer to point to prev (which is now 4), and point 4's right pointer to 6. Then update prev to 6.

Then we traverse to the node 8, which has no left subtree, so we modify its left pointer to point to prev (6 at this time), and point the right pointer of 6 to 8. Then update prev to 8.

Then we go back to the node 10, which has a left subtree, so we modify its left pointer to point to prev (which is now 8), and point 8's right pointer to 10. Then update prev to 10.

Then we traverse to the node 12, which has no left subtree, so we modify its left pointer to point to prev (10 at this time), and point the right pointer of 10 to 12. Then update prev to 12.

Then we go back to the node 14, which has a left subtree, so we modify its left pointer to point to prev (12 at this time), and point 12's right pointer to 14. Then update prev to 14.

Then we traverse to the node 16, which has no left subtree, so we modify its left pointer to point to prev (14 at this time), and point 14's right pointer to 16. Then update prev to 16.

Finally we go back to the root node 10 and go left from it to find the leftmost node 4, which is the head node of the doubly linked list. Just return 4.

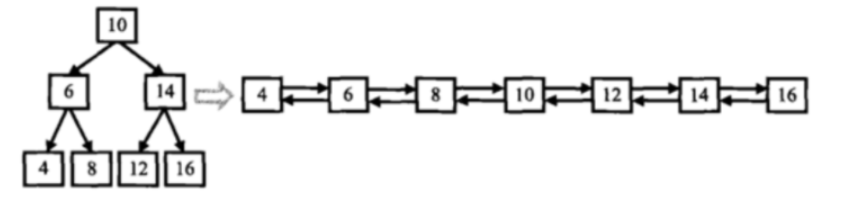
At this point, the binary search tree has been converted into the following doubly linked list:

NULL <-> 4 <-> 6 <-> 8 <-> 10 <-> 12 <-> 14 <-> 16 <-> NULL

Code - add comments

/*
struct TreeNode {
    int val; // 节点的值
    struct TreeNode *left; // 左子节点的指针
    struct TreeNode *right; // 右子节点的指针
    TreeNode(int x) : // 构造函数，初始化节点的值和子节点指针
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
    
    
  public:
    void InOrderConvert(TreeNode* cur, TreeNode*& prev) {
    
    
        if (cur == nullptr) // 如果当前节点为空，直接返回
            return;
        InOrderConvert(cur->left, prev); // 递归遍历左子树
        //这里cur出现的顺序就是中序
        cur->left = prev; // 将当前节点的左指针指向前一个节点
        if (prev) // 如果前一个节点不为空，将其右指针指向当前节点
            prev->right = cur;
        prev = cur; // 更新前一个节点为当前节点

        InOrderConvert(cur->right, prev); // 递归遍历右子树
    }
    TreeNode* Convert(TreeNode* pRootOfTree) {
    
    
        TreeNode* prev = nullptr; // 初始化前一个节点为空
        InOrderConvert(pRootOfTree,
                       prev); // 调用辅助函数，中序遍历二叉树，并修改指针

        TreeNode* head = pRootOfTree; // 初始化头节点为根节点
        while (head &&
                head->left) {
    
     // 循环找到最左边的节点，即双向链表的头节点
            head = head->left;
        }


        return head; // 返回头节点
    }
};

end of this section